2. 无锡透平叶片有限公司,江苏 无锡 214023
2. Wuxi Turbine Blade Co., Ltd., Wuxi 214023, China
随着模具精锻技术的快速发展,其在航空叶片制造中得到了广泛应用.据统计,国外航空叶片制造方法80%是运用模具精锻技术[1-2].相对于国外,我国航空叶片精锻模具设计经验不足,设计参数的确定较为困难.由于叶片生产批量小、种类繁多、型面复杂且精度要求高,使得叶片模具的设计任务大大增加[3].经工程验证,在叶片精锻成形的过程中,当锻造条件一定时,模具设计参数对叶片成形力和模具磨损有着极大影响,模具设计参数选择不合理会导致叶片充型不完整和模具磨损加剧[4-6].因此,研究如何优化模具设计参数计算方法、合理选择模具设计参数、减小模具磨损、提高模具设计效率,对提高企业的核心竞争力具有重要意义[7].
本文根据Archard摩擦理论,借助Deform-3D软件, 对不同设计参数下的叶片模具精锻成形过程进行了模拟仿真,运用正交试验分析了模具成形角度、桥部厚度、桥部宽度3种因素对叶片成形和模具磨损的影响,得到了最优设计参数组合,并对该参数的计算方法进行了优化改进;最后对参数优化后的模具磨损量进行了实验验证.
1 模具磨损分析 1.1 Archard模型理论Archard理论是计算摩擦磨损的常用模型.在该理论中,材料硬度和磨损系数为定值.在实际热模锻成形过程中,模具材料的硬度与磨损系数并非是定值,它们随温度的变化而变化.Lee等[8]和Behrens等[9]通过摩擦磨损实验分析了模具钢材料(H13)在不同锻造温度下的材料硬度、磨损系数与锻造温度之间的关系,提出了修正的Archard理论:
| $W = K(T)\frac{1}{{H(T)}}\int p v{\rm{d}}t, $ | (1) |
| $H(T) = 9216.4{T^{ - 0.505}}, $ | (2) |
| $K(T) = [29.29\ln (T) - 168.73]{10^{ - 6}}. $ | (3) |
式中:K(T)为材料磨损系数,单位cm3/(N·m);H(T)为材料硬度,单位N/mm2;W为磨损量,单位mm;p为锻造压力,单位MPa;v为材料流动速度,单位mm/s;T为模具温度,单位℃.
在不同锻造时刻,模具型腔不同位置处的压力、温度、材料流动速度不同[10-11],故第j时间段第i处的磨损量表示为
| $ \Delta {w_{ij}} = {K_{ij}}(T)\frac{1}{{{H_{ij}}(T)}}{p_{ij}}{v_{ij}}\Delta {t_j}. $ | (4) |
总磨损量为
| ${W_i} = \int_0^n {{K_{ij}}} (T)\frac{{{p_{ij}}{v_{ij}}}}{{{H_{ij}}(T)}}{\rm{d}}t. $ | (5) |
式中:pij为模具型腔i处第j时间段的压力;vij为模具型腔i处第j时间段材料流动速度;n为锻造次数.
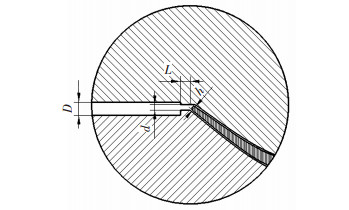
1.2 基于正交试验的有限元仿真分析发动机轴线与叶片模具型面截面弦长线的夹角称为锻造成形角度,如图 1所示.桥部厚度、桥部宽度如图 2所示.

|
图 1 叶片成形角度示意图 Fig.1 Diagram of blade forming angle |
|
图 2 模具桥部局部结构示意图 Fig.2 Local structure schematic diagram of bridge die h—飞边厚度;d—桥部厚度;L—桥部宽度;D—仓部厚度 |
正交试验设计方法是组合参数选优的一种方法[12-13],本文以锻造成形角度、桥部厚度、桥部宽度3个模具设计参数为因素,采用三因素四水平设计方法对某型号叶片锻造成形过程进行模拟仿真,研究不同设计参数因素水平对锻造载荷、横向侧向力和模具磨损的影响.因素水平表见表 1,正交试验方案见表 2.
| 表 1 因素水平变量值 Table 1 Factor level variable values |
| 表 2 正交试验方案设计表 Table 2 Orthogonal test design |
Deform-3D作为有限元工艺仿真软件,主要用于模锻金属成型分析、热处理等,在模锻成形仿真时,需设置模拟对象属性和锻造边界条件[14-16]:
1) 锻件材料为Ti-6Al-4V(TC4),锻造终锻温度950 ℃,最小网格尺寸为1 mm,最大网格尺寸为2 mm.
2) 模具材料为4Cr5MoSiV1(H13),上模参考温度250 ℃,温度允许变化范围250~540 ℃,运动方向+Y;下模固定,参考温度300 ℃,温度允许变化范围300~540 ℃;最小网格尺寸1 mm,最大网格尺寸2 mm,硬度55HRC.
3) 接触关系.磨损模型设为Archard模型, 热传导系数为2, 摩擦因子为0.3.
4) 模拟行程控制.由有限元分析理论知,锻造步长约为最小单元网格尺寸的0.2~0.3倍,故设置锻造步长为0.25 mm.根据模具锻造时的初始位置和最终成形位置,估算锻造行程约为24 mm,故锻造步数设为100步.
借助模拟软件Deform-3D对16种方案的3种考察对象进行模拟仿真,得到的结果如表 3所示.由表 3计算得出的各因素水平偏差量总和如表 4所示.
| 表 3 各方案模拟结果 Table 3 Simulation results of each program |
| 表 4 各水平因素偏差量总和 Table 4 Sum of the levels of the amount of deviation |
为了综合评估考察对象对各因素、各水平的依赖性,需对上述试验数据进行直观分析和方差分析.
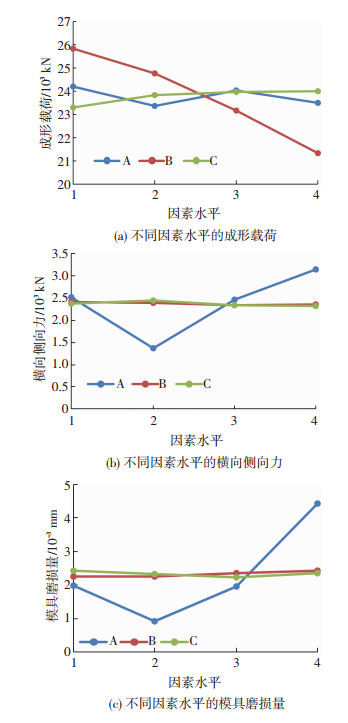
根据图 3的直观分析图,可以得出不同因素水平与考察对象之间的关系.由图 3(a)可知,成形载荷最佳组合为A2B4C1;由图 3(b)可知,横向侧向力最佳组合为A2B3C4;由图 3(c)可知,模具磨损量最佳组合为A2B2C3.
|
图 3 不同因素水平与考察对象之间的关系 Fig.3 Relationship between different factors and subjects: (a) forming load at different factor levels; (b) transverse force at different factor levels; (c) die wear at different factor levels |
由表 5方差分析可知考察对象对各因素的依赖显著性关系.对于锻造载荷,因素A、C表现为不显著,B显著;对于横向侧向力,因素A表现为高度显著,B、C不显著;就模具磨损量而言,因素A表现为高度显著,B、C不显著.
| 表 5 方差分析表 Table 5 Analysis of variance |
通过直观分析和方差分析可知:桥部厚度为影响锻造载荷的主要因素,故选择B4;成形角度为影响横向侧向力和模具磨损量的主要因素,故选择A2.因素C对上述3个考察对象的影响较小,考虑到本文讨论的主题是模具磨损,根据直观分析选择C3.因此, 得到的模具设计参数的最优组合为A2B4C3.
2 模具参数设计方法优化 2.1 桥部参数设计方法优化根据上述分析可知,桥部厚度越大锻造载荷越小,但考虑到叶片实际锻造成形规律,由于叶片飞边处较薄,在叶片锻造成形时,过大的桥部厚度会使得模具型腔充型不完整,导致叶片残缺,如图 4所示.因此, 适当增加锻造时的材料流动阻力,更有利于模具充型完整.根据热锻过程中材料的流动特性和流体热力学理论[17-18],经过大量的模拟和工程实验,对以往的经验设计法进行了改进,得出叶片成形规律与叶片飞边厚度之间的关系:在桥部厚度约为飞边厚度的1.1倍,桥部宽度约为飞边厚度的2倍时,叶片成形规律和锻造载荷最好:

|
图 4 d=1.3h时材料的流动特性 Fig.4 Flow characteristics of the material at d=1.3h |
d=1.1h(mm)(优选值:0.6、0.8、1.0、2.4)
L=2.0h(mm)(优选值:1、2、2.5、3、4)
故应选择最优设计参数组合为A2B3C3.
2.2 成形角度设计方法优化由上述分析可知,模具锻造成形角度对模具的横向侧向力影响很大,成形角度设计不合理将会增加模具侧向力,从而导致其横向移位,加剧模具磨损,使得模具使用寿命严重缩短.现阶段成形角度的设计一般采用几何构造法[19],其设计过程复杂、误差较大,需要多次实验对其进行验证,严重影响了模具的开发周期.成形角度的确定原则:应保证模具型腔曲面在锻造方向上的投影面积最大.本文在分析几何构造法设计成形角度的基础上,通过对多个叶片叶身截面的曲率分析,结合多次模拟仿真和工程实验,对锻造成形角度的设计方法进行了优化,获得了叶身截面与锻造成形角度之间的关系模型,即三截面平均法:
| $ {\alpha _0} = \frac{{{\alpha _1} + {\alpha _2} + {\alpha _3}}}{3}. $ | (6) |
式中, α1、α2、α3分别为叶尖、叶身中点、叶根与叶身截交面的弦长线与发动机轴线夹角.
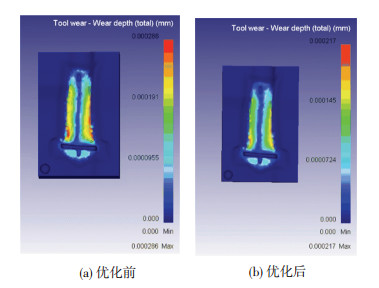
3 实验验证选用优化前后的最优设计参数组合A2B3C3的某型号航空叶片精锻模具,通过软件模拟和工程实验对其摩擦磨损量进行分析验证.在叶片精锻成形时,最大允许模具磨损量为0.2 mm,运用软件对参数优化前后的模具进行锻造仿真,得到的模具磨损量如图 5(a)和(b)所示,参数优化前其一次锻造的最大磨损量为0.286 μm,锻造寿命约为699次;参数优化后其一次锻造的最大磨损量为0.217 μm,锻造寿命约为921次,其寿命相差24%.这种现象的发生主要是因为优化前模具设计参数存在误差,这种误差会导致模具所受锻造压力、横向侧向力和金属局部流动速度增加,又由于模具在高温高压下工作,其表面屈服应力下降,金属的高温、高速流动会导致模具磨损增加.
|
图 5 参数优化前后模具磨损 Fig.5 Die wear before and after parameter optimization: (a) die wear before parameter optimization; (b) die wear after parameter optimization |
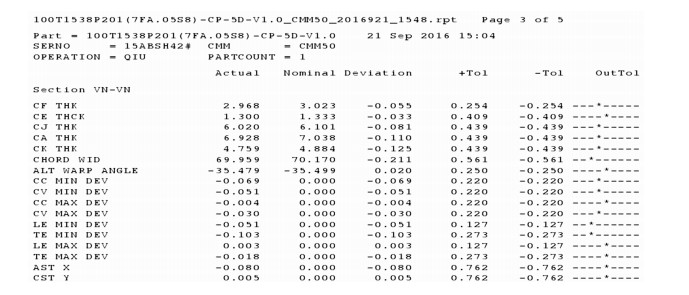
选用优化后的参数组合A2B3C3,实体模具如图 6所示,通过锻造实验对该模具磨损量进行验证.图 7为其三坐标测量报告,可以看出:模具最大磨损量为0.211 μm,其锻造寿命约为947次;且最优组合设计参数模具的模拟结果和实验结果具有较好的一致性.

|
图 6 参数优化后的模具实体 Fig.6 Die entity after parameter optimization |
|
图 7 模具检测报告 Fig.7 Die test report |
1) 数值仿真结果表明,成形角度是影响侧向力和模具磨损的主要因素,15°为该模具的最优成形角度;桥部厚度是影响材料流动性的主要因素,1.1h为其最优桥部厚度,超过1.3h叶片成形规律难以控制.通过模拟仿真和材料的流动性分析,最终确定了模具设计参数的最优组合为A2B3C3.
2) 通过分析现有模具参数设计方法和大量的模拟、实验数据,得出了模具设计参数与叶片自身结构之间的关系,对成形角度和桥部结构参数的设计方法进行了改进,简化了模具参数设计的过程,提高了模具参数设计的精度,减少了模具设计参数的修正次数和模具的试锻次数.
3) 通过模拟仿真对参数优化前后的叶片模具的摩擦磨损进行了分析,得出二者的锻造寿命相差约24%.最后通过工程实验对一般设计参数和最优设计参数叶片模具进行摩擦磨损验证,通过分析得出:二者寿命相差近2倍,且A2B3C3模具的模拟结果和实验结果的一致性较好.即借助正交试验设计方法和有限元模拟仿真为航空叶片模具设计参数选优和锻造寿命预测提供了一种方法.
| [1] |
刘维伟. 航空发动机叶片关键制造技术研究进展[J]. 航空制造技术, 2016, 516(21): 50-56. LIU Weiwei. Research progress on key manufacturing technology of aeroengine blades[J]. Aeronautical Manufacturing Technology, 2016, 516(21): 50-56. DOI:10.16080/j.issn1671-833x.2016.21.050 |
| [2] |
余小鲁, 李付国. TC4钛合金风扇转子叶片模锻工艺和性能研究[J]. 锻造技术, 2010, 35(3): 19-21. YU Xiaolu, LI Fuguo. Research on die forging process and mechanical properties of titanium alloy TC4 fan propeller blade[J]. Forging & Stamping Technology, 2010, 35(3): 19-21. |
| [3] |
AMANO C X R S. On the development of turbo machine blade aerodynamic design system[J]. International Journal for Computational Methods in Engineering Science & Mechanics, 2009, 10(3): 186-196. |
| [4] |
JHAVAR S, PAUL C P, JAIN N K. Causes of failure and repairing options for dies and molds[J]. Engineering Failure Analysis, 2013, 9(36): 1-7. |
| [5] |
KIM D H, LEE H C, KIM B M, et al. Estimation of die service life against plastic deformation and wear during hot forging processes[J]. Journal of Materials Processing Technology, 2005, 166(3): 372-380. DOI:10.1016/j.jmatprotec.2004.07.103 |
| [6] |
KIM B M, LEE H C, KIM K H. Estimation of die service life in hot forging, considering lubricants and surface treatments[J]. Proceedings of the Institution of Mechanical Engineers. Part B: Engineering Manufacture, 2003, 217(7): 1011-1022. DOI:10.1243/09544050360686860 |
| [7] |
YANG Hai, ZHANG Dinghua, LI Shan, et al. Research and application of collaboration between design & manufacturing for precision forged blade[J]. Advanced Materials Research, 2012, 490-495: 2534-2539. DOI:10.4028/www.scientific.net/AMR.490-495 |
| [8] |
LEE R S, JOU J L. Application of numerical simulation for wear analysis of warm forging die[J]. Journal of Materials Processing Technology, 2003, 140: 43-48. DOI:10.1016/S0924-0136(03)00723-4 |
| [9] |
BEHRENS B A, BOUGUECHA A, HADIFI T, et al. Numerical and experimental investigations on the service life estimation for hot-forging dies[J]. Key Engineering Materials, 2012, 504-506: 163-168. DOI:10.4028/www.scientific.net/KEM.504-506 |
| [10] |
GAO Tao, YANG He, LIU Yuli. Backward tracing simulation of precision forging process for blade based on 3D FEM[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(2): 639-644. |
| [11] |
JIA W P, XIN L, JING C, et al. Temperature/stress field numerical simulation of hollow blade produced by laser rapid forming[J]. Chinese Journal of Lasers, 2007, 34(9): 1308-1312. |
| [12] |
孙宪萍, 刘强强, 杨兵, 等. 基于磨损正交试验的温挤压模具优化设计[J]. 润滑与密封, 2016, 41(6): 73-76. SUN Xianping, LIU Qiangqiang, YANG Bing, et al. Optimization design on warm extrusion die based on orthogonal experiments of wear[J]. Lubrication Engineering, 2016, 41(6): 73-76. DOI:10.3969/j.issn.0254-0150.2016.06.016 |
| [13] |
占亮, 李霞, 孙礼宾, 等. 基于正交试验的曲轴热锻工艺参数优化[J]. 锻造技术, 2014, 39(7): 10-13. ZHAN Liang, LI Xia, SUN Libin, et al. Design optimization of process parameters of crankshaft die forging based on orthogonal experiment[J]. Forging & Stamping Technology, 2014, 39(7): 10-13. DOI:10.13330/j.issn.1000-3940.2014.07.003 |
| [14] |
BARIANI P F, BRUSCHI S, DAL NEGRO T. Integrating physical and numerical simulation techniques to design the hot forging process of stainless steel turbine blades[J]. International Journal of Machine Tools and Manufacture, 2004, 44(9): 945-951. DOI:10.1016/j.ijmachtools.2004.01.020 |
| [15] |
XU L, YAN P G, HUANG H Y, et al. Numerical simulation of the final stage nozzle blade with dolphin profile in the steam turbine[J]. Jilin Daxue Xuebao, 2008, 38: 28-33. |
| [16] |
WANG X J, LIAO G L, ZHU D, et al. Numerical simulation on suction performance of steam turbine hollow stationary blade[J]. Turbine Technology, 2012(3): 195-197. |
| [17] |
齐广霞, 曹娜, 史丽坤. GH4169合金叶片终锻成形宏观场量规律数值模拟[J]. 锻造技术, 2011, 36(5): 155-162. QI Guangxia, CAO Na, SHI Likun. Laws of macro-field numerical simulation in GH4169 alloy blade final forging[J]. Forging & Stamping Technology, 2011, 36(5): 155-162. |
| [18] |
郑丹星. 流体与过程热力学[M]. 北京: 化学工业出版社, 2010.
|
| [19] |
《透平机械现代制造技术丛书》编委会. 叶片制造技术[M]. 北京: 科学出版社, 2002.
|
 2019, Vol. 27
2019, Vol. 27


