氮化钛(TiN)是一种过渡金属氮化物,因其优良的高硬度、抗氧化、耐磨耐腐蚀性及高的载流子浓度而被广泛应用于工业生产中.最近,相关的应用性研究报道越来越多[1-3],涉及低辐射薄膜、燃料电池、太阳电池、集成电路、纳米生物技术等领域.另外,在表面等离激元(surface plasmon)的研究中,由于传统贵金属易氧化等缺点,导致Ag和Au在应用方面受到局限,使得很多学者把寻找替代材料的目光转向了氮化钛[4-7].
研究表明,氮化钛(TiN)薄膜是通过离子键、金属键和共价键结合而成,其中氮的p轨道能量低于费米能级,导致材料中自由电子的运动类似于金属键的d电子轨道上的运动,增加了TiN的导电性,因此TiN薄膜具有类似于金、银等贵金属薄膜的光学性能,在低辐射镀膜玻璃中具有广泛应用.在氮化钛薄膜光学色散关系的研究中,研究人员提出了不同的色散模型[8-11],基本形式均为Drude模型混合Lorentz谐振子模型.这种色散关系对于掺杂氮化钛薄膜也同样适用,例如掺杂B、Cr、Al、Zr、Ta、Mo等元素,原因在于掺杂比例较小时不会改变氮化钛晶格的面心立方结构.在氮化钛相关的理论计算研究中,Ern等[12]采用缀加平面波(augmented plane wave)的方法计算了TiN的能带结构和态密度,Xiao等[13]利用CASTEP软件包讨论了氮化钛作为太阳辐射屏蔽材料的可行性.
在反应磁控溅射制备工艺中,氮气流量对氮化钛薄膜光学性质的影响非常显著[11].因此,本文将根据理论计算的结果,着重讨论了氮分压的改变对薄膜光学性质的影响.实验中通过固定其他工艺参数,仅改变氮气流量,沉积了不同氮气流量下的TiN薄膜,采用Drude-3Lorentz色散模型拟合了椭圆偏振光谱仪测试出的薄膜介电函数谱,分析了氮气流量对TiN薄膜光学性能的影响.
1 实验与计算 1.1 实验及表征采用CS300型直流磁控溅射镀膜机制备薄膜样品,衬底为载玻片,靶材为99.995%纯度的Ti靶,本底真空为2.4×10-3 Pa,溅射电流为1 A,电压250 V,沉积时间9 min,沉积温度392 ℃,衬底旋转速率20 r/min,工作压强0.5 Pa,氩气流量为40 sccm,氮气流量分别为1.6和1.4 sccm.采用美国J.A.Woollam公司VASE型椭圆偏振光谱仪测量薄膜的介电函数和折射率,光谱测试范围为240~1 100 nm,扫描步长10 nm.采用日本岛津公司的UV-3100型分光光度计测试薄膜的光谱透过率,光谱测量范围为380~2 500 nm.
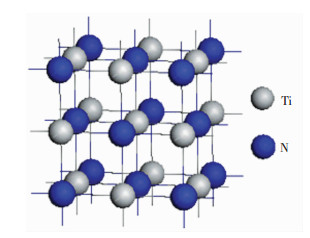
1.2 计算方法理想的TiN是面心立方结构,属于PM3M空间群,晶格常数a=b=c=0.424 nm.晶胞结构为NaCl结构,计算采用的晶格模型如图 1所示.
|
图 1 TiN的晶格结构 Fig.1 Lattice structure of TiN |
计算采用基于密度泛函理论的CASTEP软件包来完成.采用周期性边界条件,利用广义梯度近似(GGA)的PBE方法处理电子间的交换关联能.电子波函数通过平面波基失组扩展,并采用超软赝势描述离子实与价电子间的相互作用,选取Ti和N的价电子组态分别为:N,2s22p3;Ti,3s23p63d24s2.在倒易的k空间中,平面波截止能Ecut选取为340 eV,系统总能量和电荷密度在Brillouin区的积分使用Mokhorst-Pack方案,k网格点选取为4×4×4,以保证体系能量和构型在准完备平面波基水平上收敛,其自洽收敛精度为1×10-6 eV/atom.晶格模型的优化采用BFGS算法,优化参数如下:原子间相互作用力收敛标准为0.3 eV/nm,单原子能量收敛标准为1×10-5 eV/atom,晶体内应力收敛标准为0.05 GPa,原子的最大位移收敛标准为0.000 1 nm.最后,再以此为基础计算TiN的光学性质.
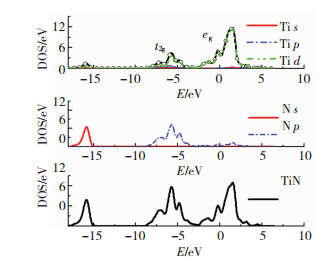
2 结果与讨论 2.1 态密度为分析TiN的光学性质及色散关系,首先计算TiN的电子态密度,包括分波态密度和总态密度,图 2中能量为0的位置代表Fermi能级.
|
图 2 TiN的电子态密度 Fig.2 Electric density state of TiN |
由图 2可以看出,TiN呈现出金属性,根据相关实验测试结果,其载流子浓度约为1022 cm-3,很好地说明了TiN能在集成电路充当电极及作为热反射涂层应用于低辐射薄膜的原因.N原子的s轨道呈现出强烈的局域化特征,且N2p态和Ti3d态产生了强烈的杂化,正是由于这种杂化作用使得晶格中的Ti—N键既类似于金属键,又类似于共价键和离子键,TiN薄膜的高硬度、耐高温和耐腐蚀特性就来源于此.
不考虑电子自旋时,Ti原子的d轨道由于最近邻的6个N原子所形成的八面晶体场的作用,部分简并被消除,在Fermi能级下2.5 eV处劈裂成了三重简并的t2态和二重简并的e态.
2.2 色散模型与光学性质根据跃迁的选择定则Δl=0、±1,可以分析出TiN晶体的能级跃迁主要发生在N p→Ti d(t2态、e态)以及Ti d轨道的t2→e态之间.因此,本文依据第一性原理计算的结果,结合经典的色散模型[14]和已有关于TiN色散模型的研究[11],提出了适合于TiN的Drude-3Lorentz色散模型(简记为D3L模型),并采用该模型拟合氮化钛薄膜的介电函数谱:
| $ \begin{array}{l} \varepsilon (E) = {\varepsilon _1} + {\rm{i}}{\varepsilon _2} = {\varepsilon _\infty } - \frac{{E_{{\rm{pu}}}^2}}{{{{(\hbar w)}^2} + {\rm{i}}\gamma (\hbar w)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k = 1}^3 {\frac{{{A_k}}}{{E_k^2 - {{(\hbar w)}^2} - {\rm{i}}{B_k}(\hbar w)}}} \end{array} $ |
式中:ε∞表示正离子实背景;Drude项表征材料的金属吸收作用;Epu是未考虑屏蔽效应的等离子体共振频率;γ为阻尼系数;ℏ是普朗克常数;ω是角频率;Lorentz项代表3种能级跃迁,Ek为跃迁频率,Ak表征跃迁的强度,Bk是跃迁的阻尼系数.
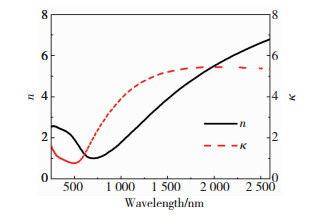
图 3为第一性原理计算出的TiN光学常数,可以看出,在600和1 950 nm处折射率(n)和消光系数(κ)相等,表明这2个频率附近的光波能量能够被TiN所完全吸收.600 nm附近高能处的光波能量主要用来激发TiN产生等离子体共振,而1 950 nm附近低能处的光波能量主要被晶格中光学支声子所吸收[15].此外,高折射率和高消光系数也表明了TiN呈强烈的金属性.
|
图 3 第一性原理计算出的TiN光学常数 Fig.3 Optical constants of TiN calculated by first-principle theory |
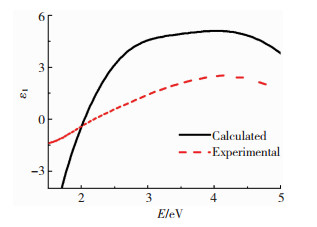
进行理论计算体材料时考虑了周期性边界条件,得到了材料的介电函数和光电性质.比较TiN介电函数的理论计算值和实验值,结果见图 4,可以发现,等离子体共振频率都在2.1 eV附近,充分说明ωp是材料的一种内蕴属性,而ε1之间强弱的差别反映了理论计算的体材料和实验中的薄膜材料光学性质的不同之处.
|
图 4 TiN介电函数的实验值与计算值比较 Fig.4 Comparison between experimental and calculated values of dielectric function of TiN |
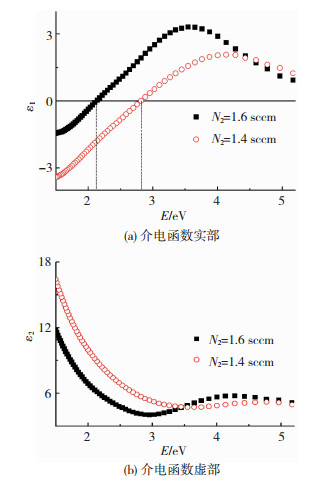
图 5给出了不同氮分压下TiN薄膜的介电函数谱,可以看出,随着氮分压的降低,薄膜的等离子体共振频率ωp(ε1=0)向高能方向移动,这和已有的研究结论相吻合[16].
|
图 5 TiN薄膜的介电函数 Fig.5 Dielectric function of TiN films: (a) real part; (b) imaginary part |
TiN薄膜中的电子主要由Ti原子所提供,随着氮分压的降低,形成薄膜的过程中,没有足够的N原子参与Ti—N键的形成,导致薄膜中Ti原子含量相对丰富,使得薄膜的载流子浓度(N′)增加,金属性增强.根据ωp2=N′e2/(ε0m*)可知,随着薄膜载流子浓度的增加,等离子体共振频率(ωp)将变大.
采用D3L模型拟合薄膜的椭圆偏振光谱,结果见表 1,可以发现,薄膜的吸收随着氮分压的降低而增强,这是由于氮分压降低时TiN晶格中没有足够的N原子,形成的薄膜中缺陷将会增加,当电子在薄膜中运动时,由于晶格缺陷及晶界散射等作用,所产生的吸收作用将会增强.如表 1所示,随着氮分压的降低,Epu的增加反映了薄膜的金属性增强.阻尼系数γ的增大说明薄膜的缺陷增加,与此同时,3种跃迁的频率位置却并未发生显著的变化,分别位于1.4、4.3和5.6 eV左右,只是每种跃迁的强度和阻尼系数产生了改变.这充分说明了薄膜中Ti原子和N原子的成键方式未发生改变,所形成的TiN依然具有面心立方结构,只是晶格的缺陷随着氮分压的降低而有所增加.
| 表 1 用D3L模型拟合得到的参数值 Table 1 Parameter values fitted by the D3L model |
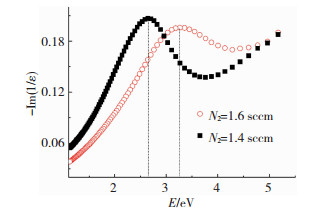
能量损失函数定义为-Im(1/ε)=ε2/(ε12+ε22),该函数包含了单电子的激发或激子、等离激元等共振现象所产生的吸收作用,反映了薄膜中电子在外界特定频率电磁波下的响应特征.图 6给出了根据薄膜的介电函数谱而得出的能量损失函数图.
|
图 6 TiN薄膜的能量损失函数 Fig.6 Energy loss function of TiN films |
TiN薄膜的能量损失函数谱在1.5~4.0 eV内出现很强的峰值.这种强烈的吸收作用主要由薄膜等离子体共振所产生.峰值位置分别位于2.64和3.26 eV处,与ε1=0处的频率位置2.14、2.82 eV相比,都向高能方向偏移,原因在于薄膜中除了等离子体共振的能量吸收外,还存在其他形式的能量吸收,这种能量吸收也反映在有关TiN表面等离子体共振特性的研究中,反映在介电函数谱中,即介电函数实部ε1=0时,ε2不为0.
峰的宽度也随着氮分压的降低而展宽,反映了薄膜中产生吸收作用的阻尼系数增强,从参数γ的增大也可以得到佐证.此外,薄膜的能量损失函数在5 eV以后会出现另一个峰值.根据D3L模型拟合的结果,可确定该峰值位置在5.57 eV处,与薄膜中的能带跃迁相关.
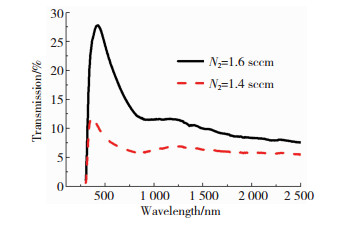
2.4 薄膜的透射率薄膜的光谱透射率曲线能够很好地反映薄膜的光学性质,图 7是分光光度计测出的薄膜透射率曲线, 可以看出,随着氮气流量的降低,薄膜的峰值透过率由28%降为13%.根据前面的讨论,薄膜金属性的增强使得电子吸收了更多可见光区的能量,是导致透过率下降的主要原因.此外,通过能量损失函数图发现,较低氮分压的样品的吸收峰在高能区域扩展得很宽,正是这种宽能量区域的吸收作用,在一定程度上也降低了薄膜的可见光透过性能.
|
图 7 TiN薄膜的光谱透射率 Fig.7 Spectral transmittance of TiN films |
本文采用基于密度泛函理论的广义梯度近似方法,详细计算并讨论了TiN的电子结构与光学特性.根据TiN的态密度,得出了适合TiN的色散模型.通过分析计算出的光学常数,得出了TiN中存在的主要吸收形式.通过对比介电函数的理论计算值和实验值,得出了TiN的等离子体共振频率在2.1 eV左右.
根据理论计算得出的色散模型,拟合了通过反应磁控溅射技术制备的TiN薄膜的介电函数谱,并讨论了氮分压对薄膜光学性质的影响.结果表明:随着氮分压的降低,薄膜中的N原子含量降低,使得自由载流子浓度增加,ωp向高能方向移动,且由于薄膜中没有足够的N原子和Ti原子成键,导致薄膜的缺陷增加,晶格缺陷和晶界散射所产生的吸收作用增强,阻尼系数增大,膜层在可见光区的透过率下降.
| [1] |
MAHIEU S, LEROY W P, VAN A K, et al. Sputter deposited transition metal nitrides as back electrode for CIGS solar cells[J]. Solar Energy, 2011, 85(3): 538-544. |
| [2] |
BIRKHOLZ M, EHWALD K E, KULSE P, et al. Ultrathin TiN membranes as a technology platform for CMOS-integrated MEMS and BioMEMS devices[J]. Advanced Functional Materials, 2011, 21(9): 1652-1656. DOI:10.1002/adfm.201002062 |
| [3] |
POPOVIC M, NOVAKOVIC M, SCHMIDT E, et al. Low-loss and tunable near-zero-epsilon titanium nitride[J]. Optical Materials, 2017, 72: 775-780. DOI:10.1016/j.optmat.2017.07.035 |
| [4] |
SHANKERNATH V, LAKSHUN N K, GHANASHYAM K M, et al. Optical response of ultra-thin titanium nitride films on brass and gold plated brass surfaces[J]. Materials Research Bulletin, 2017, 85: 121-130. DOI:10.1016/j.materresbull.2016.09.006 |
| [5] |
BONSE J, KIRNER S V, KOTER R, et al. Femtosecond laser-induced periodic surface structures on titanium nitride coatings for tribological applications[J]. Applied Surface Science, 2017, 418: 572-579. DOI:10.1016/j.apsusc.2016.10.132 |
| [6] |
QIU G, NG S P, WU C L. Label-free surface plasmon resonance biosensing with titanium nitride thin film[J]. Biosensors and Bioelectronics, 2018, 106: 129-135. DOI:10.1016/j.bios.2018.02.006 |
| [7] |
KAISAR N, HUANG Y T, JOU S, et al. Surface-enhanced Raman scattering substrates of flat and wrinkly titanium nitride thin films by sputter deposition[J]. Surface & Coatings Technology, 2018, 337: 434-438. |
| [8] |
WATTOO A G, XU Cheng, YANG Lijing, et al. Design, fabrication and thermal stability of spectrally selective TiAlN/SiO2 tandem absorber[J]. Solar Energy, 2016, 138: 1-9. DOI:10.1016/j.solener.2016.08.053 |
| [9] |
MENG Jianping, LIN Xiaopeng, FU Zhiqiang, et al. Optical design of Cu/Zr0.2AlN0.8/ZrN/AlN/ZrN/AlN/Al34O62N4 solar selective absorbing coatings[J]. Solar Energy, 2017, 146: 430-435. DOI:10.1016/j.solener.2017.03.012 |
| [10] |
AN Liqiong, ALI S T, SONDERGAARD T, et al. Optimization of TiAlN/TiAlON/SiN solar absorber coatings[J]. Solar Energy, 2015, 118: 410-418. DOI:10.1016/j.solener.2015.05.042 |
| [11] |
PATSALAS P, LOGOTHETIDIS S. Optical, electronic, and transport properties of nanocrystalline titanium nitride thin films[J]. Journal of Applied Physics, 2001, 90(9): 4725-4734. DOI:10.1063/1.1403677 |
| [12] |
ERN V, SWITENDICK A C. Electronic band structure of TiC, TiN and TiO[J]. Phys Rev, 1965, 137(6A): 1927-1936. DOI:10.1103/PhysRev.137.A1927 |
| [13] |
XIAO Lihua, SU Yuchang, CHEN Hongyang, et al. Solar radiation shielding material for windows TiN studied from first-principles theory[J]. Applied Physics Letters, 2011, 99(6): 061906. DOI:10.1063/1.3624709 |
| [14] |
FOX M. Optical Properties of Solids[M]. New York: Oxford University Press, 2001.
|
| [15] |
STEFAN A. Plasmonics: Fundamentals and Applications[M]. New York: Springer Science + Business Media LLC, 2007.
|
| [16] |
KANG J H, KIM K J. Structural, optical, and electronic properties of cubic TiNx compounds[J]. Journal of Applied Physics, 1999, 86(1): 346-350. DOI:10.1063/1.370736 |
 2019, Vol. 27
2019, Vol. 27


