泡沫钢作为近年来开发的一种新型金属多孔材料,具有高比强度、比模量高、耐高温、轻质、吸能减震、多孔过滤等优点[1-5].相比于泡沫铝,泡沫钢具有高于泡沫铝的强韧性和抗冲击吸能性,同时还可与钢结构共容等特点[6-8],因此,这种新型轻质泡沫钢材料,在航空航天、汽车船舶等领域有着广阔的应用市场,如航空航天工业应用的超轻质构件与散热面板、汽车的缓冲装置、吸声降噪材料、新型开发的坦克防爆装甲及防弹衣等[9-11].
目前国内外有关泡沫钢的制备方法主要有熔体金属发泡法、空心球烧结法、渗流铸造法、电沉积法、粉末冶金法等方法[11-12].熔体金属发泡法对于高熔点的钢铁材料,发泡过程中孔隙率和孔均匀性很难控制;空心球法工艺流程长、成本高;渗流铸造法对预制件要求高,渗流后去除预制体困难;沉积法对设备要求高,难以制备大块体材料.因此,开发一种工艺简单、成本低、孔隙率高、孔分布均匀的泡沫钢制备工艺成为解决上述问题的关键.本文采用粉末冶金烧结-溶解法制备泡沫钢,相比于其他方法,烧结-溶解法不仅流程周期较短、成本低,而且可以通过控制加入造孔剂的含量、尺寸形态来控制孔隙率和孔形貌[8].对于粉末冶金烧结-溶解法,造孔剂的选择对控制泡沫钢的孔形结构和孔隙率至关重要.Bekoz和Oktay等[6, 13]以碳酰胺颗粒为造孔剂制备出孔隙率为48%~71%的泡沫钢样品,并研究了造孔剂体积分数对孔隙率和力学性能的影响.Gülsoy [14]等人也以碳酰胺为造孔剂成功制备出孔隙率为40%~60%的泡沫钢样品.Joshi等[15]以针状碳酰胺为造孔剂制备了孔隙率为40%~60%的不锈钢泡沫样品.从前述公开报道的文献来看,碳酰胺是目前制备泡沫钢使用最普遍的一种造孔剂.然而,碳酰胺作为造孔剂尚存在许多不足,由于其熔点低,在低温下分解,容易引起压坯坍塌,且工艺过程较为复杂.本文尝试选择一种新的造孔剂,即以CaCl2颗粒为造孔剂,CaCl2化学稳定性好、熔点高、无毒、水溶性好、低成本,有望成为制备高熔点泡沫金属的理想造孔剂材料.
目前,对于泡沫金属材料吸能特性的分析研究主要集中在泡沫铝上,有关泡沫钢在吸能方面的研究鲜有报道.本文采用粉末冶金烧结-溶解法制备了孔隙率、孔径不同的几组泡沫钢试样,分析讨论孔隙率和孔形貌对泡沫钢压缩应力应变曲线及屈服平台应力的影响,以及孔隙率对吸能值和理想吸能效率的影响,并与泡沫铝的吸能性能进行对比分析.随着制备工艺的发展以及结构-性能关系的深入研究,将推动泡沫钢材料综合性能的进一步优化,未来的实际应用价值将会逐步显现.
1 实验泡沫钢的基体原料为雾化法生产的430L不锈钢粉, 成分(质量分数)为17%Cr、3%Ni、1.25%Mn、0.75%Si、0.12%C、0.035%P、0.03%S,其余均为Fe,颗粒粒径≤40 μm),造孔剂为无水CaCl2.图 1为CaCl2颗粒和不锈钢粉形貌图.泡沫钢制备工艺路线如图 2所示.

|
图 1 CaCl2颗粒(a)和不锈钢粉(b)形貌 Fig.1 Morphology of CaCl2 particles (a) and stainless steel (b) powder |
|
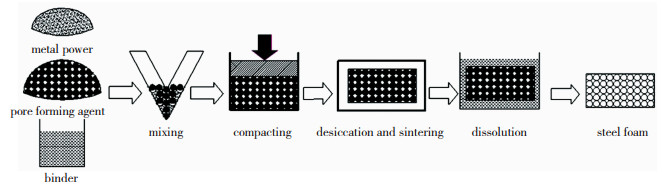
图 2 泡沫钢的制备工艺 Fig.2 Processing of steel foam fabrication |
首先将430L不锈钢粉和无水CaCl2颗粒按一定配比均匀混合,并在混合料过程中添加适量的粘结剂,约占总量的3%~5%,置于V型混料机中进行充分混合.将混合均匀的粉料置于压坯模具中,采用单向加载液压机(JYE-2008)进行压坯.坯料取出放入恒温干燥箱中,干燥温度为120~150 ℃,保温2~4 h,使坯体中的粘结剂(无水乙醇)充分去除.将干燥完成后的坯体置于气氛(氩气)烧结炉中,烧结温度为1 100 ℃,保温2~3 h,烧结完成后随炉冷却.样品取出后充分进行水洗,通过水溶去除残余CaCl2,干燥完成后即得到实验所用试样.
采用X衍射仪(XL30ESEM-TMP,荷兰)和扫描电子显微镜(QUANTA200,荷兰)对样品的微观组织结构进行观察分析,利用万能试验机对泡沫钢试样进行准静态压缩测试(AG-IC100kN,日本),试样尺寸为25 mm(d)×25 mm(h),压头移动速率为1 mm/min.泡沫钢样品的实际孔隙率通过测量体积和质量并测算得出.图 3为烧结温度1 100 ℃、保温时间120 min、孔隙率为78.82%的泡沫钢试样.

|
图 3 泡沫钢试样图 Fig.3 Samples of steel foam |
图 4为1 100 ℃、保温2 h的烧结条件下泡沫钢的孔结构形貌.由图 4(a)和(b)观察可见,泡沫钢内部孔结构分布较为均匀,孔径分布在1.2~1.8 mm,孔壁内表面粗糙.从图 4(c)和(d)可见,孔壁上有大量由金属颗粒烧结收缩形成的微孔,相邻孔之间通过孔壁上的微孔连通,孔壁厚度约为100~150 μm.同时,由图 4(d)可以清晰地看到,原始的金属颗粒间产生烧结冶金结合,颗粒合并长大形成基体晶粒,晶粒尺寸在10~20 μm.

|
图 4 泡沫钢孔结构组织形貌图 Fig.4 Microstructure and morphology of cell of steel foam:(a)porous morphology; (b)single cell; (c)cell wall; (d)metallurgical bonding of metal particles |
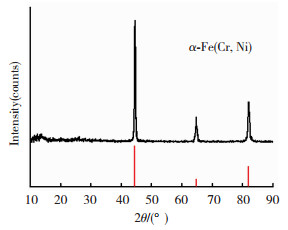
图 5为泡沫钢试样的XRD谱图.由图 5可知,衍射峰为试样的基体组成相,标定为α-Fe固溶体,由于原料成分中含有的Cr和Ni元素,固溶于Fe中,形成α-Fe(Cr,Ni)固溶体.
|
图 5 泡沫钢的XRD谱图 Fig.5 XRD pattern of steel foam |
图 5中除可以标定的α-Fe峰外,没有其他衍射峰存在,说明样品在烧结过程中,没有发生明显氧化,同时造孔剂CaCl2已基本除尽.
2.2 压缩变形行为 2.2.1 应力应变曲线将几组不同孔隙率和孔径的泡沫钢样品进行准静态压缩测试,得到如图 6所示的压缩应力应变曲线.由图 6可知,泡沫钢在外界载荷作用下,第1阶段为弹性变形阶段,应力随应变呈线性增加,第2阶段为塑性屈服变形阶段,应力随应变的增加缓慢上升,应力应变曲线表现为一段宽度的平台变形区,平台的起始点应力称为泡沫材料的屈服平台应力和屈服强度,第3阶段为压缩密实阶段,应力随应变的增大而急剧增加.
|
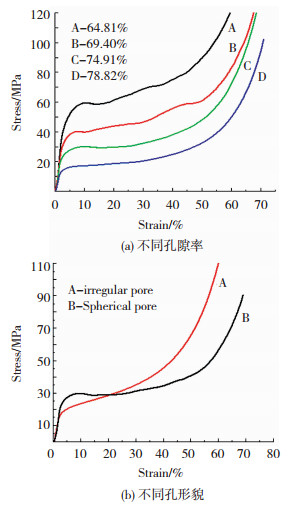
图 6 泡沫钢的应力-应变曲线 Fig.6 Stress-strain curves of steel foam:(a)different porosities; (b)different pore morphologies |
图 6(a)为孔径相近、孔隙率在64%~80%的泡沫钢试样在压缩变形过程的应力-应变曲线,可以看到, 各曲线相对比较平滑,均具有明显的3个变形阶段.在外力作用下承担载荷的是泡沫钢的孔壁结构,孔隙率越大,孔数量越多,孔壁越薄,孔壁所能承受的应力越低,泡沫钢试样的抗压强度也越低.当孔隙率为64.81%、69.40%、74.91%、78.82%时,其对应的屈服平台应力为59.37、39.61、29.76、17.04 MPa.根据Gibson-Ashby经典公式[16],如式(1)和(2)所示.
| $ {\sigma _{{\rm{pl}}}} = 0.3{\sigma _{{\rm{ys}}}}{\left( {\frac{{{\rho ^ * }}}{{{\rho _{\rm{s}}}}}} \right)^{1.5}}, $ | (1) |
| $ {\sigma _{{\rm{pl}}}} = 0.3{\varphi ^{1.5}}{\sigma _{{\rm{ys}}}}{\left( {\frac{{{\rho ^ * }}}{{{\rho _{\rm{s}}}}}} \right)^{1.5}} + {\sigma _{{\rm{ys}}}}\left( {1 - \varphi } \right)\left( {\frac{{{\rho ^ * }}}{{{\rho _{\rm{s}}}}}} \right). $ | (2) |
式(1)为开孔结构模型,式(2)为闭孔结构模型.式中:σpl为平台应力;σys为实体金属的屈服强度(430L不锈钢的屈服强度为330 MPa);ρ*为样品的实际密度;ρs为实体钢的密度;(1-θ)=ρ*/ρs,其中θ为样品的实际孔隙率,ρ*/ρs≤φ≤1,本实验中φ取0.5作为理论计算.按公式(1)和(2),分别对孔隙率为64.81%、69.40%、74.91%、78.82%的开孔与闭孔泡沫钢样品所对应的理论平台应力进行计算,所得平台应力范围依次为:20.67 ~65.37 MPa、16.76 ~56.42 MPa、12.44 ~45.79 MPa、9.65 ~38.36 MPa.实验样品相应孔隙率的平台应力介于开孔和闭孔之间,说明实验所制备的样品其内部孔结构介于开孔与闭孔之间,可以称之为半开孔结构.
图 6(b)为孔隙率相同(约为75%)孔形貌不同的泡沫钢试样的应力-应变曲线,孔形貌不规则的泡沫样品屈服强度低于孔形貌规则呈近球形的样品,当应力超过屈服强度后,其应力应变曲线变化的斜率大于规则孔样品的斜率.原因是:孔形貌不规则的样品,孔壁厚度不均匀且曲率度不同,在压缩过程中,曲率度小且壁薄的局部区域容易出现应力集中而先产生变形,局部变形迅速扩展为多个变形带引起整体变形,致使样品进入压实致密化阶段加快,最终导致样品的应力随应变增长的速率加快.而孔形貌规则呈近球形的泡沫钢样品,孔分布和孔壁厚度较为均匀,不容易出现局部应力集中而导致屈服变形,屈服强度高,在压缩过程中,孔壁受力均匀且大部分的孔洞同时发生弯曲变形,变形带扩展缓慢,因而存在一个较长的平台变形阶段,致使应力随应变的增长呈现缓慢变化.由此可知,材料内部的孔洞形貌对样品的整体力学性能有着较大的影响.
2.2.2 变形过程图 7是孔隙率为76%的泡沫钢试样在轴向准静态压缩下的变形过程.图 7显示,样品中存在局部孔形貌不规则,在压缩变形过程中,表现出变形过程的不均匀性.由图 7可以看出,在应变量达到5%前,孔洞结构无明显变形,此阶段对应着应力应变曲线中的弹性变化.当应变量由5%增至10%时,变形过程开始进入塑性屈服平台阶段,在孔形貌不规则且孔壁较薄的孔壁处率先发生塑性变形,如图 7中应变量为10%的区域1所示,其他孔结构未发生明显变形.当应变量达15%时,其区域1的变形带开始进行延伸并逐渐影响到与其相邻的孔结构,发生变形的孔数量开始增多,变形带扩展,同时随着应力增加会触发新的变形带形成, 如区域2所示.当应变量进一步增加至20%~25%时,被初始变形带影响的孔也开始发生明显的变形,导致周围区域发生变形形成新的变形区域带,如变形区域3和4所示,同时,样品的弯曲变形开始表现为横向呈鼓形膨胀,如变形区域5和6所示.当应变量达到30%~35%时,其横向膨胀变形明显加强,样品的中部区域开始形成新的剪切变形带,如变形区域7和8所示.样品在变形后期,大部分的孔洞已完全坍塌并逐渐闭合,材料的密实程度不断增加,应力随应变的增大而不断增加,从应力-应变曲线也证实了这一点.

|
图 7 泡沫钢的变形过程 Fig.7 Deformation process of steel foam |
从泡沫钢的压缩变形过程可以看出,泡沫试样的压缩变形机理与孔形貌和孔壁的厚度存在紧密的联系.在受到外界载荷时,孔壁较薄且曲率半径较小的区域容易出现应力集中,孔壁变形会率先从这些地方开始,并导致孔坍塌,同时,率先发生变形的区域会影响相邻孔壁的变形,从而引起周围的孔结构也随着变形,这些连续发生的变形区域形成了变形带,最终变形带扩展导致泡沫试样整体变形.
2.3 能量吸收性能能量吸收值是反映多孔材料在压缩过程中是否具备良好吸能性能的一个重要特性,其表示单位体积的试样被压缩到一定应变量时所吸收的能量,即样品压缩应力-应变曲线所包含的面积.能量吸收值的计算公式见式(3).
| $ C = \smallint _0^{{\varepsilon _m}}\sigma {\rm{d}}\varepsilon . $ | (3) |
式中:C代表单位体积泡沫试样的能量吸收值,即样品在应变量为εm时,应力-应变曲线与坐标轴所包围的面积;εm为任意应变;σ为应力,即为应变ε的函数.
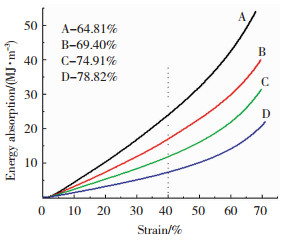
图 8为不同孔隙率泡沫钢的能量吸收值-应变曲线.由图 8可知,当应变量低于5%时,泡沫钢的能量吸收值较少,这是因为泡沫金属在受到外界载荷时,其吸能主要发生在塑性平台屈服阶段,此阶段表现为样品弹性区域的吸能情况.同时,曲线可以明显反映出在到达压缩密实阶段之前,单位体积泡沫钢的能量吸收值随应变量的增加呈线性增加.当应变达到40%时,曲线出现拐点,斜率逐渐降低.这是因为能量吸收值的大小由平台应力与平台宽度两个参数共同决定,孔隙率大的样品虽然有着相对较宽的平台区域,但其所对应的平台应力相对较低,且平台应力的影响明显大于平台区域宽度.因此,其对应的曲线以下的面积相对较小.对于泡沫材料,其优良的吸能性能主要取决于适当的平台区域宽度以及相对较高的平台应力.
|
图 8 不同孔隙率泡沫钢的能量吸收-应变曲线 Fig.8 Energy absorption-strain curves of steel foams with different porosities |
表 1和表 2为不同孔隙率的泡沫钢与泡沫铝在不同应变下的能量吸收值(泡沫钢的孔径范围为2.36~3.35 mm,泡沫铝的孔径范围为1.60~4.00 mm).对比表 1和表 2中泡沫钢与泡沫铝在不同应变下的能量吸收值,可以得出,在孔隙率相近时(泡沫钢为69.40%,泡沫铝为70%),泡沫钢单位体积的能量吸收值约为泡沫铝的5~7倍.孔隙率分别为78.82%与60%的泡沫钢和泡沫铝,在相同应变下,前者的能量吸收值仍为后者的1.17~1.69倍.由此可以得出,泡沫钢在吸能性能上相比于泡沫铝具有更突出的优点,是一种良好的吸能材料.
吸能效率是表征泡沫材料吸能性能的另外一个重要指标,Miltz等提出用吸能效率(E)和理想吸能效率(I)来评价泡沫材料的能量吸收能力[19],如式(4)和式(5)所示.
| $ E = \frac{{\smallint _{^0}^{{\varepsilon _m}}\sigma \left( \varepsilon \right){\rm{d}}\varepsilon }}{{{\sigma _{\rm{m}}}}}, $ | (4) |
| $ I = {\rm{ }}\frac{{\smallint _{^0}^{{\varepsilon _m}}\sigma {\rm{d}}\varepsilon }}{{{\varepsilon _{\rm{m}}}{\sigma _{\rm{m}}}}}. $ | (5) |
式中:E为吸能效率,即吸能值与应力的比值,用来反映材料吸能的最优工作状态;I为理想吸能效率,即在任意应变下,应力应变曲线所包围的面积与其对应的矩形面积之比;σm为εm对应的应力.I反映了一个真实的材料与理想吸能材料的接近程度,即理想吸能效率越大,材料越接近理想吸能材料.
| 表 1 不同应变下泡沫钢的能量吸收值(CSF) Table 1 Energy absorption of steel foam with different strain |
| 表 2 不同应变下泡沫铝的能量吸收值(CAF)[17-18] Table 2 Energy absorption of aluminum foam with different strain[17-18] |
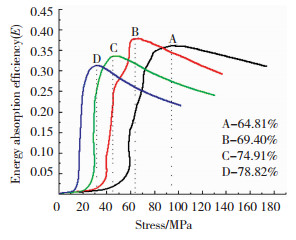
图 9为不同孔隙率泡沫钢试样的E-σ图.由图 9可知,孔隙率为65%~79%泡沫钢样品吸能效率范围为0.38~0.31,吸能效率峰值对应的应力按孔隙率增序排列依次为94.56、63.20、44.25、31.67 MPa,此应力值接近于应力-应变曲线压缩密实开始阶段的应力,样品在最大吸能效率下工作时,能够充分发挥其吸能性能.
|
图 9 不同孔隙率泡沫钢的吸能效率-应力曲线 Fig.9 Energy absorption efficiency-stress curves of steel foams with different porosities |
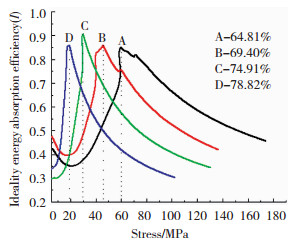
图 10为不同孔隙率泡沫钢的I-σ图,可以看到,按孔隙率降序排列,其最大理想吸能效率依次为0.86、0.91、0.86和0.85,对应的应力分别为18.94、29.86、45.33和59.52 MPa,此应力值接近于不同孔隙率泡沫钢试样应力-应变曲线的平台应力,对于屈服平台阶段不明显的应力应变曲线,Paul[20]等认为平台应力可采用10%应变时的应力.从理想吸能效率的角度来评估材料吸能性能的优劣时,可以认为以上4种不同孔隙率的泡沫钢样品均为性能优良的理想吸能材料.
|
图 10 不同孔隙率泡沫钢的理想吸能效率-应力曲线 Fig.10 Ideality energy absorption efficiency-stress curves of steel foams with different porosity |
1) 以430L不锈钢粉为原料、无水CaCl2为造孔剂,采用粉末冶金烧结-溶解法成功制备了孔隙率为64%~80%、孔径为1~4 mm的泡沫钢样品,样品孔形貌规则、孔径分布均匀.
2) 经1 100 ℃保温120 min烧结,金属颗粒形成冶金结合并合并形成晶粒,基体为α-Fe(Cr,Ni)固溶体,基体中分布着由造孔剂去除留下的内孔,内孔孔壁中有微孔存在,使孔结构之间形成有效连通.
3) 在压缩变形过程中,变形区首先发生在孔形不规则且孔壁较薄处,后诱发周围孔变形并形成多个变形带.泡沫钢试样压缩屈服平台应力随着孔隙率的增加而减小,当孔隙率为64.81%、69.40%、74.91%、78.82%时,其对应的屈服平台应力为59.37、39.61、29.76、17.04 MPa.在孔隙率相同的条件下,孔形为近球形的泡沫试样屈服平台应力远高于孔形不规则的试样.
4) 当应变量为40%时,孔隙率为64.81%~78.82%的泡沫钢样品其能量吸收值为23.92 ~7.32 MJ/m3,在孔隙率近似相同时,泡沫钢单位体积的能量吸收值为泡沫铝的5~7倍.4种不同孔隙率的泡沫钢,理想吸能效率均在0.85以上,最大理想吸能效率为0.91,说明泡沫钢是一种理想的吸能材料.
| [1] |
奚正平, 汤惠萍. 烧结金属多孔材料[M]. 北京: 冶金工业出版社, 2009. XI Zhengping, TANG Huiping. Sintered metal porous material[M]. Beijing: Metallurgical Industry Press, 2009. |
| [2] |
MONDAL D P, JAIN H, DAS S, et al. Stainless steel foams made through powder metallurgy route using NH4HCO3 as space holder[J]. Materials and Design, 2015, 88: 430-437. DOI:10.1016/j.matdes.2015.09.020 |
| [3] |
LI Z Q, XI C Q, JING L, et al. Effect of loading rate on the compressive properties of open-cell metal foams[J]. Materials Science and Engineering A, 2014, 592(592): 221-229. |
| [4] |
SZYNISZEWSKI S T, SMITH B H, HAJJAR J F, et al. The mechanical properties and modeling of a sintered hollow sphere steel foam[J]. Materials and Design, 2014, 54(2): 1083-1094. |
| [5] |
KETEP S F. Stainless steel foam pushes the current provided by microbial bioanodes for bioelectrochemical systems[J]. Energy and Environmental Science, 2014, 6: 1633-1637. |
| [6] |
BEKOZ N, OKTAY E. Effects of carbamide shape and content on processing and properties of steel foams[J]. Journal of Materials Processing Technology, 2012, 212: 2109-2116. DOI:10.1016/j.jmatprotec.2012.05.015 |
| [7] |
SMITH B H, HAJJAR J F. Steel foam for structures: A review of applications, manufacturing and material properties[J]. Journal of Constructional Steel Research, 2011, 71(1): 1-10. |
| [8] |
GUO K S, LI M C, Gong Q, et al. Experimental investigation on steel foams fabricated by sintering-dissolution process[J]. Materials and Manufacturing Processes, 2015, 31(12): 1597-1602. |
| [9] |
SZYNISZEWSKI S, SMITH B H, HAJJAR J F, et al. Local buckling strength of steel foam sandwich panels[J]. Thin-Walled Structures, 2012, 59(4): 11-19. |
| [10] |
FU Y H. Analysis of collision characteristic of oil tank based on steel-foam sandwich and iceberg[J]. Ship Engineering, 2014, 36: 158-161. |
| [11] |
MUTLU I, OKTAY E. Production and characterization of Cr—Si—Ni—Mo steel foams[J]. Indian Journal of Engineering and Materials Sciences, 2011, 18(3): 227-232. |
| [12] |
SZYNISZEWSKI S T, SMITH B H, HAJJAR J F, et al. The mechanical properties and modeling of a sintered hollow sphere steel foam[J]. Materials and Design, 2014, 54(2): 1083-1094. |
| [13] |
BEKOZ N, OKTAY E. High temperature mechanical properties of low alloy steel foams produced by powder metallurgy[J]. Materials and Design, 2014, 53(1): 482-489. |
| [14] |
GüLSOY H, German RM. Sintered foams from precipitation hardened stainless steel powder[J]. Powder Metallurgy, 2008, 51: 350-353. DOI:10.1179/174329008X286703 |
| [15] |
JOSHI S, GUPTA G, SHARMA M, et al. Synthesis and characterization of stainless steel foam via powder metallurgy taking acicular urea as space holder[J]. Material Science Research India, 2015, 12: 43-49. DOI:10.13005/msri/120108 |
| [16] |
GIBSON L J, ASHBY M. Cellular solids: Structures and properties-second edition[M]. Cambridge: University Press, 1997.
|
| [17] |
刘欢.泡沫铝材料的吸能与防爆特性研究[D].沈阳: 东北大学, 2014. LIU Huan. Energy absorption and explosion proof ability of aluminum foam[D]. Shenyang: Northeastern University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10145-1015559750.htm |
| [18] |
杨旭东, 石建, 程洁, 等. 填加造孔剂法制备泡沫铝及其吸能性能[J]. 航空材料学报, 2017, 37(2): 55-62. YANG Xudong, SHI Jian, CHENG Jie, et al. Fabrication of aluminum foam by space-holder method and the energy absorption properties[J]. Journal of Aeronautical Materials, 2017, 37(2): 55-62. DOI:10.11868/j.issn.1005-5053.2016.000117 |
| [19] |
MILTZ J, GRUENBAUM G. Evaluation of cushion properties of plastic foams compressive measurements[J]. Polymer Engineering and Science, 1981, 21(15): 1010-1014. DOI:10.1002/pen.760211505 |
| [20] |
PAUL A, RAMAMURTY U. Strain rate sensitivity of a closed-cell aluminum foam[J]. Materials Science and Engineering A, 2000, 281(1): 1-7. |
 2019, Vol. 27
2019, Vol. 27


