2. 中南大学 机电工程学院,长沙 410083
2. School of Mechanical and Electronic Engineering, Central South University, Changsha 410083, China
金属材料加工制备过程中伴随着残余应力的产生,残余应力对材料的结构稳定、疲劳强度和零件的服役、寿命有着重要的影响[1-3].作为材料表面完整性关键指标的表面应力测试和评估一直受到国内外研究者关注,例如X-ray衍射技术广泛应用到应力测试中以评价材料表面应力状况[4],但是受专用设备和层深(10 μm)局限,使得其他方法得到极大发展,如钻孔法(ASTM E837-2001)、磁性法、超声法和压痕法(GB/T 24179—2009)[5-6].钻孔法属于准破坏力学方法,对材料损坏很小,但是其操作简便,测试精度也逐步提高,适合于零件的各部位和非均匀应力分布状况,其测试原理就是通过去除孔材料,而释放孔周围应力引起变形,通过应变反求区域内应力,Zhu和Blödorn等在文献[7-8]中有阐述,在表面应力测试中应用非常普遍.
目前,钻孔法已经发展到逐层细化,将表面应力层深描述由原来2 mm提高到500 μm以内,徐颖强、Magnier、Gaikhe等研究了逐层钻孔法在复合材料、有色金属和非金属材料领域的应用[9-12].随着钻孔技术的发展,钻孔产生的附加应力越来越小,测量结果越来越精确.Andreas等[13-14]用超短脉冲镭射技术在不锈钢材料上钻孔,通过控制脉冲能量、频率和数量,可以在30 μm到1 mm范围内生成高质量的小孔.Richert等[15-16]利用电子散斑干涉技术ESPI对0.5 mm孔深逐层应力释放直接测量,而无需进行应变测量,提高了测试时间和效率,但该技术对压应力和样本表面质量非常敏感,往往也会造成数据偏差.郑建毅等[17]采用有限元求取5阶应力释放校准系数,在工具钢表面分5层在2.5 mm深度描述了材料表面应力分布,但没有考虑材料各向异性.Schuster等[18]研究在各向异性材料上如果进行各向同性应力评估,将会导致显著应力偏差,并通过采用更多维校准系数来减小这种偏差,但计算和数据处理较复杂.Gibmeier等[19]则研究表明,使用特定校准系数可以较好完成对有明显织构的材料进行应力评估.
本文针对7075铝合金挤压板加工后表面应力测量,在考虑挤压材料各向异性条件下,利用ANSYS构建了试样的三维有限元模型,对中心圆直径为5.13 mm的B型应变花进行校准系数标定.最后利用力学计算模型,在100 μm表层深度上还原非均匀残余应力分布.
1 逐层钻孔法力学建模 1.1 逐层钻孔法原理逐层钻孔法是利用小孔周围应力释放后的应变来间接获取小孔处应力的微损方法.如图 1所示,该方法的原理是:材料内部存在应力场,在材料表面逐步钻一小孔时,每一步进给都会使得孔周围应力被释放,而原应力场失去平衡,这时小孔周围会产生释放变形(应变)来使得应力场重新达到平衡.每一步钻深进给都会使得当前不同深度的应力释放,而贴在构件表面的应变花将测得每次释放应变量.
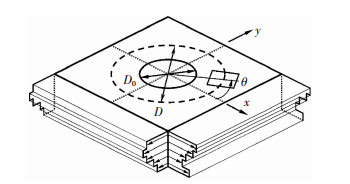
|
图 1 非均匀残余应力试样 Fig.1 Nonuniform residual stress profile in specimen |
如图 1所示非均匀应力情况,第j步钻孔后所测得的表面释放应变与之前1≦j≦n所有孔深材料内的残余应力相关,可按式(1)计算[20]:
| $ \begin{aligned} \varepsilon_{\mathrm{n}}=\frac{1+v}{E} & \sum\limits_{j=1}^{n} a_{n j}\left(\sigma_{x j}+\sigma_{y j}\right)+\frac{1}{E} \sum\limits_{j=1}^{n} b_{n j} \tau_{x y j} \sin 2 \theta+\\ & \frac{1}{E} \sum\limits_{j=1}^{n} b_{n j}\left(\sigma_{x j}-\sigma_{y j}\right) \cos 2 \theta \end{aligned} $ | (1) |
式中:εn为小孔应变;E为弹性模量;δxj为在第j步平面上X方向的应力;δyj为在第j步平面上Y方向的应力;τxyj为在第j步平面上X、Y方向的剪切应力.标定系数矩阵anj和bnj表示当钻进到第n步孔深时,由于受到第j步孔深处的残余应力影响所引起的释放应变的影响系数.
图 2列举了采用三步钻孔法时孔截面的一系列变化情况.标准应变花的标定系数采用有限元方法计算获得.
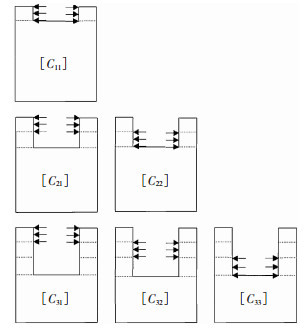
|
图 2 逐层三步钻孔原理 Fig.2 Drilling principle of the three-step IHDM |
本模型三向应变花的角度分别为0°、45°和90°,3个方向上的应变分别用εn1、εn2和εn3表示.挤压板坯沿挤压方向为应变花对应的0°,正交方向为应变花对应的90°.做了标准试验后进行材料拉伸实验,结果见图 3,计算后发现,材料弹性模量在挤压方向为85 GPa,正交方向为81 GPa,数值相差约5%.Schuster等[18]研究了在各向异性材料上如果以各向同性应力评估,将会导致显著应力偏差.鉴于此,由于实验材料为挤压板材,具有各向异性,因此需要对计算公式进行修正,以符合测试要求.

|
图 3 拉伸实验 Fig.3 Tensile experiments |
则式(1)转变为
| $ \left\{\begin{array}{l} {\varepsilon_{n 1}} &{=} {\frac{1+υ}{E_{1}} \sum\limits_{j=1}^{n} a_{n j}\left(\sigma_{x j}+\sigma_{y j}\right)+} \\ & {\frac{1}{E_{1}} \sum\limits_{j=1}^{n} b_{n j}\left(\sigma_{x j}+\sigma_{y j}\right)}, \\ {\varepsilon_{n 2}}&= {\frac{1+υ}{E_{2}} \sum\limits_{j=1}^{n} a_{n j}\left(\sigma_{x j}+\sigma_{y j}\right)+} \\ & {\frac{1}{E_{2}} \sum\limits_{j=1}^{n} b_{n j} \tau_{xy j}}, \\ {\varepsilon_{n 3}}&= {\frac{1+υ}{E_{3}} \sum\limits_{j=1}^{n} a_{n j}\left(\sigma_{x j}+\sigma_{y j}\right)}- \\ & {\frac{1}{E_{3}} \sum\limits_{j=1}^{n} b_{n j}\left(\sigma_{x j}-\sigma_{y j}\right)}. \end{array}\right. $ | (2) |
为了更好地表示应力和应变间的相互关系,引入矩阵Cnj,则
| $ \varepsilon_{n}=C_{n j} \sigma_{n}, $ | (3) |
| $ \begin{array}{c} \varepsilon_{n} =\left[\begin{array}{c} {\varepsilon_{n 1}} \\ {\varepsilon_{n 1}} \\ {\varepsilon_{n 2}} \end{array}\right], \\ \sigma_{n} =\left[\begin{array}{c} {\varepsilon_{x n}} \\ {\varepsilon_{y n}} \\ {\varepsilon_{x y m}} \end{array}\right], \\ C_{n j}=\left[\begin{array}{ccc} {\frac{(1+v) a_{n j}+b_{n j}}{E_{1}}} & {\frac{(1+v) a_{i j}-b_{n j}}{E_{1}}} & {0} \\ {E_{1}} & {E_{1}} & {} & {} \\ {\frac{(1+v) a_{n j}}{E_{2}}} & {\frac{(1+v) a_{n j}}{E_{2}}} & {\frac{b_{n j}}{E_{2}}} \\ {\frac{(1+v) a_{n j}-b_{n j}}{E_{3}}} & {\frac{(1+v) a_{n j}+b_{n j}}{E_{3}}} & {0} \end{array}\right]. \end{array} $ |
矩阵anj和bnj与构件、应变花和小孔的几何参数有关,对于不同的钻孔步数n,这些系数是不同的.这些系数需要应用有限元模拟来计算.
由式(2)可知:E和v是材料的常数,所以通过(εnj)1和(εnj)3就可以计算出第j层的应力对第n步钻孔释放应变的影响系数,即校准系数可以由下式计算.
| $ \left(\begin{array}{l} {a_{n j}} \\ {b_{n j}} \end{array}\right)=\\ \left(\begin{array}{c} {\left(\varepsilon_{n 1}\right)_{j}} \\ {\left(\varepsilon_{n 3}\right)_{j}} \end{array}\right)/\left(\begin{array}{cc} {\frac{1+v}{E_{1}}\left(\sigma_{x j}+\sigma_{y i}\right)} & {\frac{1+v}{E_{1}}\left(\sigma_{x j}+\sigma_{y i}\right)} \\ {\frac{1}{E_{3}}\left(\sigma_{x j}-\sigma_{y i}\right)} & {-\frac{1}{E_{3}}\left(\sigma_{x j}-\sigma_{y i}\right)} \end{array}\right). $ |
为了标定7075铝合金特定校准系数矩阵,以7075铝合金板坯淬火试件为研究对象,针对逐层钻孔法测试实验步骤用ANSYS有限元软件进行模拟仿真.淬火热应力由热-力准耦合计算方法获得,仿真步骤为先对构件进行温度场及应力场计算,再进行逐层钻孔仿真.试样温度场初始温度475°,环境温度20°,换热系数16 000.温度场计算结果作为其应力场模型的初始条件,将X坐标为0的平面上所有节点添加X方向的位移约束,同样约束Y、Z方向上坐标为0的所有节点.最后将应力计算的结果作为初始条件施加到逐层钻孔仿真计算中.为了使仿真计算精确,对模型网格划分进行必要处理:模型采用扫掠方式生成网格,使模型加载时更符合平面应力分布,同时,应变花周围的网格划分保持整齐,小孔周围的网格划分更精细,其余部分较稀疏,这样有助于仿真计算更加迅速.
试样淬火后,在中间表面区域进行逐层钻孔仿真,试样尺寸为500 mm(长)×200 mm(宽)×30 mm(厚).考虑到每个材料层施加的载荷和弹性特性,该模型使用三维20节点实体单元(Solid185).图 4为三维有限元模型和应变花位置.

|
图 4 逐层钻孔法的有限元模型 Fig.4 FEM of IHDM |
对中心圆直径为5.13 mm的B型应变花测量非均匀应力的校准矩阵进行校准系数标定.试样钻孔直径为1.8 mm,每一步进给深度为0.2 mm,标定载荷δn为温度场的计算结果.通过分层加载的方法,计算出5步逐层钻孔的校准系数矩阵如下:
| $ a_{n j}=\left\{\begin{array}{l} {0.0059} \\ {0.0085} \quad {0.0129} \\ {0.0080} \quad {0.0084 \quad 0.0185} \\ {0.0066} \quad {0.0070} \quad {0.0085} \quad {0.00223}\\ {0.0050} \quad {0.0054}\quad {0.0064}\quad {0.0084}\quad {0.025} \end{array}\right. $ |
| $ b_{n j}=\left\{\begin{array}{l} {-12.8203} \\ {-10.8114} \quad {-23.9270} \\ {-7.4792} \quad {-9.2233} \quad {-31.1448} \\ {-4.7764} \quad {-5.9582} \quad {-8.7249} \quad {-36.6989} \\ {-2.9288} \quad {-3.7381} \quad {-5.4840} \quad {-8.9803} \quad {-41.344} \end{array}\right. $ |
从标定出的校准系数矩阵anj和bnj可以看出:矩阵每一行系数是递减关系,说明当孔深度增加时,残余应力释放对表层应变释放影响越来越小.所以释放应变的大小主要受近表面残余应力影响,而随着钻孔深度增大,内部残余应力对近表面释放应变的影响会逐渐消失.
为了验证校准矩阵的正确性,借助2种不同尺寸板坯淬火仿真应力场,对表层应力进行计算结果对比.设置尺寸500 mm(长)×200 mm(宽)×30 mm(厚)板坯,换热系数为25 000和尺寸500 mm(长)×200 mm(宽)×50 mm(厚)板坯,换热系数为16 000的2种仿真参数.如图 5、6所示,模型计算的应力曲线与仿真计算的应力曲线非常接近,吻合度较高,平均偏差小于10 MPa,说明逐层钻孔法使用的校准矩阵正确.
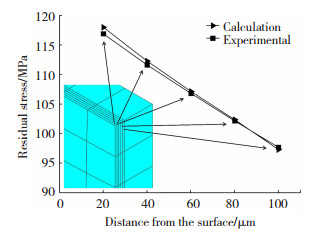
|
图 5 500 mm×200 mm×30 mm模型应力分布 Fig.5 Stress profile in 500 mm×200 mm×30 mm model |

|
图 6 500 mm×200 mm×50 mm模型应力分布 Fig.6 Stress profile in 500 mm×200 mm×50 mm model |
为了进一步验证钻孔法模型计算的正确性,需要将之与表面逐层腐蚀(每次腐蚀深度20±2 μm)后进行的XRD应力测试结果进行对比,这样就可以在表面一定深度上形成应力分布对照,其中XRD测试采用PROTO应力测试仪完成,实验流程可参考文献[21].实验试样为7075-T651铝合金挤压板坯,该材料经过固溶和预拉伸处理后,其材料力学性能参数见表 1,试样尺寸为500 mm(长)×200 mm(宽)×30 mm(厚).表面经过喷丸处理,丸粒直径0.5 mm,空气压力0.3 MPa,垂直喷射距离50 mm,喷射角度45°.喷丸目的是为了使材料表面出现加工应力.
| 表 1 试样材料力学性能参数 Table 1 Mechanical properties of materials |
根据钻孔法国际标准ASTM E 837-13a[20],实验采用的应变片是TML公司生产的FRS-2,该应变片灵敏度高,应变响应速度快,其尺寸为1.3 mm×1.5 mm,中心圆直径为5.14 mm.逐层钻孔实验采用如图 7所示的RS-200残余应力测试钻孔装置,其进给速度20 mm/s,主轴转速5 000 r/min.采用“倒锥型”的钻头,利于确保孔壁边缘的加工质量,减少钻头与孔壁的摩擦,并减小由此引起的切削应力.同时,利用温度补偿和延长空置时间来防止钻孔产生的热应变对测量释放应变造成影响.

|
图 7 钻孔所用的实验装置 Fig.7 Experimental device for drilling |
实验中,钻孔直径是1.8 mm,每步进给深度是(20±2) μm,每步钻孔时间是20 s,等待应变释放时间是40 s,在测量释放应变时收回钻头并关闭电源,应变波动 < ±2%,如表 2所示.
| 表 2 逐层钻孔测量结果 Table 2 Strain results of incremental hole-drilling |
表 2为逐层钻孔测量结果,εn1、εn2和εn3分别列出了第n步钻孔后,应变花测得3个方向释放应变量.根据测量结果,运用校准系数矩阵可以计算出各层应力.图 8为计算结果与X射线衍射应力测量结果,可以看出,XRD方法测试时测量精度在±20 MPa以内,测量实际偏差用误差棒标识.计算值均在X射线衍射(XRD)应力测量值偏差范围内,计算与实验结果偏差小于10 MPa,反映逐层钻孔法运用校准矩阵能较好描述实际应力.
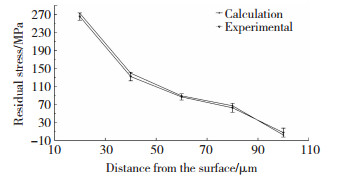
|
图 8 计算结果与X-ray结果对比 Fig.8 Comparison of X-ray results with calculation results |
为保证计算模型的准确性,需要考虑以下几个因素:1)合理选取系数矩阵阶次.文献[17]使用5阶矩阵,已经可以得到较好的仿真验证,再细分阶次意味着层深网格要更细,而加密网格对计算结果影响很小.因此,考虑到实验钻孔深度最小20 μm,并在100 μm表面深度内进行对比,最终选取5阶次矩阵; 2)计算模型中考虑了材料各向异性特征,使修正后计算的结果得以与实验结果吻合较好; 3)微观组织对力学测试的影响.实验材料为挤压板坯,铣削后表面喷丸,材料表面组织存在一定程度性状的变化,如晶粒大小、织构等.
Gibmeier等[19]研究认为,微观组织尤其是织构对模型中特定系数的影响很小,因此不会对结果产生影响.从理论分析来看,力学模型主要受弹性变形和弹性模量的影响,除非微观组织影响了宏观弹性模量,否则不会对计算形成影响.在应力测试方面,力学有损测试方法受材料宏观因素如弹性模量、各向异性特征影响较大,如钻孔法、层削法,环切法,而无损测试的XRD法则受微观组织的影响较大.逐层钻孔法属于微损力学测试方法,对微观组织变化不敏感,实验对比结果说明了这一点.
综上,该计算测试模型特点主要表现为:首先是针对性,以7075-T651铝合金为研究对象,其特定校准系数可以满足该材料应力评估需要;其次,该测试方法可以不受材料微观组织变化的影响,同时,还能够细化地描述材料表层应力分布,是应用于薄壁材料应力评估的有效方法.最后,考虑了材料各向异性特征,在理论分析中以弹性模量作为考虑各向异性计算的修正因素,完善了计算模型,并得到了实验验证,从而使得逐层钻孔法在实践中具有优越性.
4 结论1) 本文针对7075铝合金挤压板各向异性特征,通过有限元仿真模型计算非均匀应力场校准系数矩阵,完成了对力学模型计算解析函数的修正,最终获得较为完善的测试计算方法,较好地解决了铝合金材料表层应力测试问题.
2) 从有限元仿真标定的校准系数矩阵anj和bnj可以看出:矩阵每一行的系数呈递减关系,说明当孔深度增加时,残余应力的释放对表层释放应变影响越来越小.因此,逐层钻孔法并不适合材料内应力测量,但适合加工应力等这类浅层应力测试,而且不论应力分布是否均匀.
3) 运用逐层钻孔法力学模型计算的材料表层应力分布都在实验X-ray表面应力测试结果偏差范围内,计算与实验结果偏差小于10 MPa,说明该计算函数能较好描述材料表层应力分布情况.
| [1] |
何少杰, 杨文玉, 郭步鹏, 等. 机加工表面残余应力及其疲劳寿命评价的研究进展[J]. 表面技术, 2015, 44(26): 120-126+132. HE Shaojie, YANG Wenyu, GUO Bupeng, et al. Research progress on evaluation of surface residual stress and fatigue life of machined products[J]. Surface Technology, 2015, 44(26): 120-126+132. DOI:10.16490/j.cnki.issn.1001-3660.2015.06.023 |
| [2] |
王秋成, 柯映林. 航空高强度铝合金残余应力的抑制与消除[J]. 航空材料学报, 2002, 22(3): 59-62. WANG Qiucheng, KE Yinglin. Control and relief of residual stresses in high-strength aluminum alloy parts for aerospace industry[J]. Journal of Aeronautical Materials, 2002, 22(3): 59-62. DOI:10.3969/j.issn.1005-5053.2002.03.015 |
| [3] |
SINGH A, AGRAWAL A. Investigation of surface residual stress distribution in deformation machining process for aluminum alloy[J]. Journal of Materials Processing Technology, 2015, 225: 195-202. DOI:10.1016/j.jmatprotec.2015.05.025 |
| [4] |
THAIWATTHANA S, JANTAPING N, LIMTHONGKUL P. Residual stress measurement of low temperature plasma surface alloyed layer using X-ray diffraction techniques[J]. Surface Engineering, 2012, 28(4): 273-276. DOI:10.1179/1743294411Y.0000000060 |
| [5] |
杨吟飞, 张峥, 李亮, 等. 7085铝合金残余应力及加工变形的数值仿真与试验[J]. 航空学报, 2014, 35(2): 574-581. YANG Yinfei, ZHANG Zheng, LI Liang, et al. Numerical simulation and test of bulk residual stress and machining distortion in aluminum alloy 7085[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 574-581. DOI:10.7527/S1000-6893.2013.0469 |
| [6] |
李晨, 楼瑞祥, 王志刚, 等. 残余应力测试方法的研究进展[J]. 材料导报, 2014, S2: 153-158. LI Chen, LOU Ruixiang, WANG Zhigang, et al. Research progress of measuring residual stresses techniques[J]. Materials Review, 2014, S2: 153-158. DOI:10.3969/j.issn.1006.0308.2005.03.015 |
| [7] |
ZHU X, LANZA DI SCALEA F. Thermal stress measurement in continuous welded rails using the hole-drilling method[J]. Experimental Mechanics, 2017, 57(1): 165-178. DOI:10.1007/S11340-016-0204-8 |
| [8] |
BlÖDORN R, VIOTTI M R, SCHROETER R B, et al. Analysis of blind-holes applied in the hole-drilling method for residual stress measurements[J]. Experimental Mechanics, 2015, 55(9): 1745-1756. DOI:10.1007/S11340-015-0082-5 |
| [9] |
徐颖强, 李剑锋, 汪震隆. 逐层钻孔法测试多层材料残余应力数值研究[J]. 西北工业大学学报, 2009, 27(1): 39-42. XU Yingqiang, LI Jianfeng, WANG Zhenlong. Numerical analysis of incremental-step blind hole drilling method for studying relaxation coefficients A and B of residual stresses in thermal barrier coatings[J]. Journal of Northwestern Polytechnical University, 2009, 27(1): 39-42. DOI:10.3969/j.issn.1000-2758.2009.01.007 |
| [10] |
MAGNIER A, SCHOLTES B, NIENDORF T. Analysis of residual stress profiles in plastic materials using the hole drilling method-Influence factors and practical aspects[J]. Polymer Testing, 2017, 59: 29-37. DOI:10.1016/j.polymertesting.2016.12.025 |
| [11] |
SÁNCHEZ-BEITIA S, CRESPO DE ANTONIO M, ACUÑA L. Applicability of the hole-drilling procedure for stresses quantification in timber bending elements in service[J]. Construction and Building Materials, 2015, 93: 798-805. DOI:10.1016/j.conbuildmat.2015.05.091 |
| [12] |
PAWAR O A, GAIKHE Y S, TEWARI A, et al. Analysis of hole-quality in drilling GLARE fiber metal laminates[J]. Composite Structures, 2015, 123: 350-65. DOI:10.1016/j.compstruct.2014.12.056 |
| [13] |
GRUNER A, SCHILLE J, LOESCHNER U. Experimental study on micro hole drilling using ultrashot pulse laser radiation[J]. Physics Procedia, 2016, 83: 157-166. DOI:10.1016/j.phpro.2016.08.030 |
| [14] |
FINGER J, REININGHAUS M. Effect of pulse to pulse interactions on ultra-short pulse laser drilling of steel with repetition rates up to 10 MHz[J]. Optics Express, 2014, 22(15): 187900-187909. DOI:10.1364/oz.22.018790 |
| [15] |
RICKERT T. Residual stress measurement by ESPI hole-drilling[J]. Procedia CIRP, 2016, 45: 203-206. DOI:10.1016/j.procir.2016.02.256 |
| [16] |
STEINZIG M, UPSHAW D, RASTY J. Influence of drilling parameters on the accuracy of hole-drilling residual stress measurements[J]. Experimental Mechanics, 2014, 54: 1537-1543. DOI:10.1007/S.11340-014-9923-x |
| [17] |
郑建毅, 庄明凤, 郑高峰, 等. 用逐层钻孔的小孔法测量非均匀残余应力[J]. 振动、测试与诊断, 2014, 34(3): 420-427. ZHENG Jianyi, ZHUANG Mingfeng, ZHENG Gaofeng, et al. Measurement of non-uniform residual stresses by incremental hole-drilling method[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(3): 420-427. DOI:10.3969/j.issn.1004-6801.2014.03.003 |
| [18] |
SCHUSTER S, GIBMEIER J. Incremental hole drilling for residual stress analysis of strongly textured material states-A new calibration approach[J]. Experimental Mechanics, 2016, 56(3): 369-380. DOI:10.1007/S.11340-015-0104-3 |
| [19] |
GIBMEIER J, MROTZEK T, SIMON N. Reliable residual stress analysis for thin metal sheets by incremental hole drilling[J]. Materials Performance and Characterization, 2018, 7(4): 20170111. DOI:10.1520/MPC.20140111 |
| [20] |
ASTM E837-13a. Standard test method for determining residual stresses by the hole-drilling strain-gage method[S]. United States: ASTM International, West Conshohocken, PA, 2013.
|
| [21] |
廖凯, 张箫笛, 车兴飞, 等. 铝合金薄壁件加工变形的力学模型构建与分析[J]. 哈尔滨工业大学学报, 2018, 50(5): 166-172. LIAO Kai, ZHANG Xiaodi, CHE Xingfei, et al. Construction and analysis of mechanic model of deformation for Al alloy thin-walled component[J]. Journal of Harbin Institute of Technology, 2018, 50(5): 166-172. DOI:10.11918/j.issn.0367-6234.201709069 |
 2019, Vol. 27
2019, Vol. 27


