2. 天津力神动力电池系统有限公司,天津300384;
3. 上海交通大学 材料科学与工程学院,上海 200240
2. Tianjin Lishen Battery Joint-Stock Co. Ltd., Tianjin 300384, China;
3. School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
应力-应变关系即本构模型是材料控形与改性的理论基础,是利用数值模拟预报金属成形过程中缺陷、成形极限等的基本数据,因此,建立可靠和适用的本构模型是必要的。对于金属材料高温拉伸状态下本构模型的构建,关键是解决颈缩发生时与颈缩发生后应力-应变关系的问题,因为颈缩发生时颈缩处呈现三向应力状态,且颈缩截面会出现局部失稳现象。断裂过程伴随有应变、应力场多维化和不均匀化,截面形状发生改变等复杂因素[1-2],因此,仅通过单向拉伸实验无法获得材料发生颈缩后的真实应力、应变规律.
目前,从宏观、微观及宏微观角度出发建立的金属材料本构模型通常被分为3类[3]:1)基于实验数据的拟合和回归方法的现象逻辑学的模型,比如J-C模型[4]、V-K模型[5]、Arrhenius本构方程[6]、应变模型[7]和硬化模型[8]等.此类模型具有材料参数少、易验证、易于植入数值模拟中预测材料构件成形过程,但不能反映材料的物理本质,特别是在高应变速率和高温条件下.2)基于热动力学、热激活位错迁移和滑移动力学理论建立的反映物理本质的模型,比如Z-A模型[9]、PTW模型[10]、MLR模型[11-12]和考虑动态回复和动态再结晶的模型[13].3)基于人工神经网络模拟方法构建的模型(ANN模型)[14].通过对实验结果进行回归分析,基于现象逻辑学或物理的本构模型基础上获得材料常数.然而,在高温和非线性程度高的应变速率下,材料形变行为的反映和相关流动应力的许多因素也是非线性的,使得通过回归方法预测的流动应力的准确度低,因此,这类模型的应用被限制.
为准确描述材料的形变行为和断裂机制,常通过拉伸实验获得材料的本构模型.而在这类模型中,断裂应变是一个重要参数,它决定着整个形变历程中损伤累积的效果,也是衡量材料韧性的指标参数之一.因而,应变的准确测定尤为重要,特别是颈缩区域内呈非线性的应变.针对高温变形,颈缩后的应变测量方法有3种:1)直接测量法,如常用的延伸仪测量法和DIC法[15],该方法将颈缩阶段最小截面上的应变作均匀分布假设尚缺乏有效性验证.2)基于弹塑性理论,通过理论推导获得材料颈缩发生后的真实本构关系,Bridgman首次提出修正拉伸过程中的真应力、真应变的数学方程,在后期的文献中也大量运用此数学方程修正了真应力、真应变.然而,bridgman提出的修正方程不能准确描述金属热成形过程中真实的应力、应变变化,且很难测量颈缩处外轮廓的曲率,由于在热成形过程中颈缩区域处于三向应力状态,外轮廓并非呈椭球形.3)基于物理实验、有限元分析和弹塑性理论相结合的方法确定颈缩区真应力、真应变[11].Mirone[11-12]成功利用这种方法预测了材料拉伸过程中颈缩后的塑性行为,并与Bridgman模型预测值相比,平均误差低于1%,说明该方法能够准确预测颈缩后的应力应变值.
本文通过不同温度不同应变速率下高温单向拉伸实验,基于Mirone模型建立316LN不锈钢高温拉伸非线性行为的本构模型,为准确地进行数值模拟奠定基础及为制定合理的成形工艺参数提供科学依据.
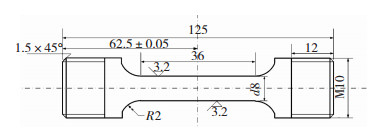
1 实验 1.1 实验材料实验材料为锻态的316LN奥氏体不锈钢,其化学成分如表 1所示,试样尺寸如图 1所示.
| 表 1 316LN奥氏体不锈钢化学成分 Table 1 Chemical composition of 316LN austenitic stainless steel (wt.%) |
|
图 1 拉伸试样尺寸图(单位:mm) Fig.1 Dimensions of the tensile specimen |
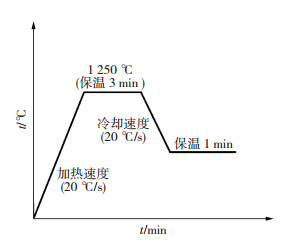
应变速率为0.001~1.0 s-1、温度为950~1 250 ℃时,在Glebble3800热模拟试验机上进行单轴拉伸实验.在拉伸试样前,先将试样以20 ℃/s加热到1 250 ℃,保温3 min,使得材料完全奥氏体化;然后将试样以20 ℃/s冷却至预设拉伸温度,保温1 min,以设定的应变速率进行拉伸至断裂为止.试样的热拉伸实验工艺如图 2所示.
|
图 2 热加工工艺图 Fig.2 Schematic diagram of hot working process |
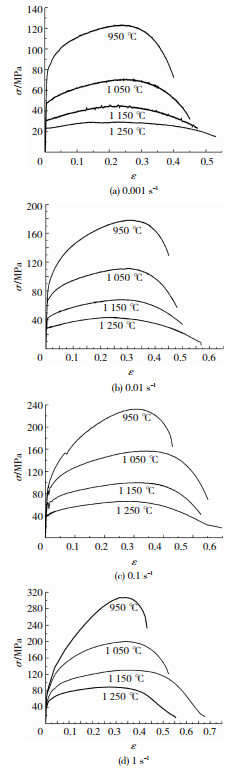
不同温度、不同应变速率条件下,316LN奥氏体不锈钢真应力-真应变曲线如图 3所示.
|
图 3 不同温度不同应变速率下316LN钢的真应力-真应变曲线 Fig.3 True stress-strain curves of 316LN steel obtained from tensile tests at different temperatures and strain rates |
由图 3可知:在同一应变速率下,峰值应力随着温度的升高而降低;当达到应力峰值时,试样标距范围内发生颈缩,处于三向应力状态;颈缩前,发生的变形量较小,应力随应变的增加迅速上升,真应力-真应变曲线随着温度的增加变化平缓,这是因为此阶段发生应变硬化;颈缩后在同一应变速率下,温度较低时应力随应变的增加急速下降并达到断裂应力,而在较高温度下应力随应变的增加缓慢下降,这是因为颈缩后发生动态再结晶软化.进一步由图 3可知,此阶段应变局部化引起非均匀变形,因此,实验所得颈缩后的真应力-真应变数据无法真实描述材料颈缩后的流变行为.本文基于Mirone提出的模型及有限元数值模拟修正颈缩后的真应力-真应变曲线.
2 316LN钢两阶段本构模型的建立 2.1 颈缩前阶段本构模型的构建颈缩前加工硬化起主导作用,且应力随应变呈幂指数形式,基于Hollomon方程(1)构建颈缩前阶段本构模型.
| $ \sigma=k \varepsilon^{n}. $ | (1) |
式中:σ是应力,ε是应变,k是强度因子,n是加工硬化指数.
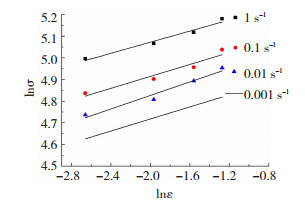
利用最小二乘法,针对图 3中颈缩前的应力、应变数据进行拟合,获得不同温度、不同应变速率下的n值(如图 4所示,以950 ℃下n值获取为例说明求n值的方法),且获得n的平均值为0.21.
|
图 4 温度为950 ℃不同应变速率下真应力与真应变间关系 Fig.4 Relationships between true stress and true strain at different strain rates and the temperature of 950 ℃ |
利用反算法获得k值为169.36.则颈缩前阶段本构模型为
| $ \sigma=169.36 \varepsilon^{0.21}. $ | (2) |
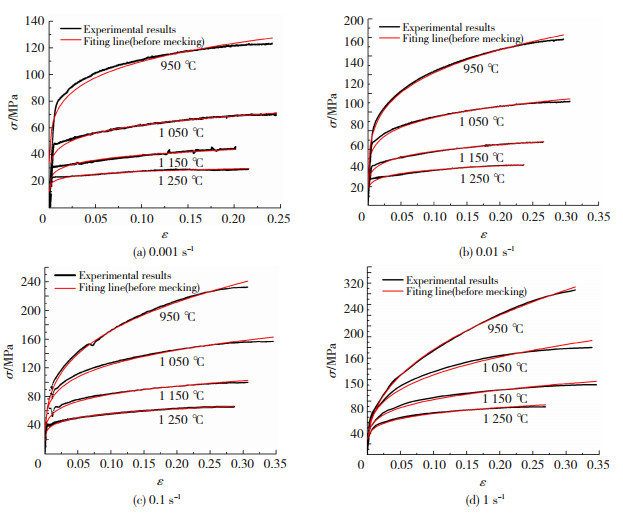
根据式(2)预测不同温度、不同应变速率下的应力-应变曲线,将其与实验获得的曲线相比,如图 5所示.由图 5可知,构建的本构模型能够准确地描述颈缩前阶段真应力-真应变关系,且平均相关度为0.963.
|
图 5 不同应变速率和温度下的颈缩前真应力真应变实验值与Hollomon模型预测值 Fig.5 Experimental values and obtained values by Hollomon model of true stress-strain before necking at different strain rates and temperatures |
颈缩前加工硬化起主导作用,且应力随应变呈幂指数形式,然而,颈缩的发生导致颈缩区处于非均匀且三轴应力状态,则颈缩后的真应力-真应变曲线偏离了真实材料的颈缩后阶段的曲线.因此,基于Mirone提出的修正颈缩发生后的真应力真应变法-MLR模型修正316LN钢的拉伸试样在拉伸过程中颈缩发生后的应力、应变.
MLR模型是利用修正应力因子MLRσ(εEq-εN)和应变因子MLRε(εEq-εN)分别乘以σTrue和σTrue获得颈缩发生后的真应力σ′和真应变ε′的函数,即:
| $ \left\{\begin{array}{l} {\sigma^{\prime}=\sigma_{\text {True }} \cdot \operatorname{MLR}_{\sigma}\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)}, \\ {\mathrm{MLR}_{\sigma}\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)=1-0.6058 \cdot\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)^{2}+\\0.6317 \cdot\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)^{3}-0.2107 \cdot\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)^{4}}, \\ {\varepsilon^{\prime}=\varepsilon_{\mathrm{True}} \cdot \operatorname{MLR}_{\varepsilon}\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)}, \\ {\operatorname{MLR}_{\varepsilon}\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)=1-0.265 \cdot\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)+\\0.241 \cdot\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)^{2}-0.074 \cdot\left(\varepsilon_{\mathrm{Eq}}-\varepsilon_{N}\right)^{3}}. \end{array}\right. $ | (3) |
式中:εN为最大载荷所对应的应变,即被认为是颈缩发生时的应变;σEq和εEq分别为实验获得的颈缩发生后瞬时真应力真应变;MLRσ(εeq, εN)表示颈缩发生后等效应力与应力之间的转换参数,MLRσ(εeq, εN)等同于颈缩后等效应变与应变之间的转换参数.
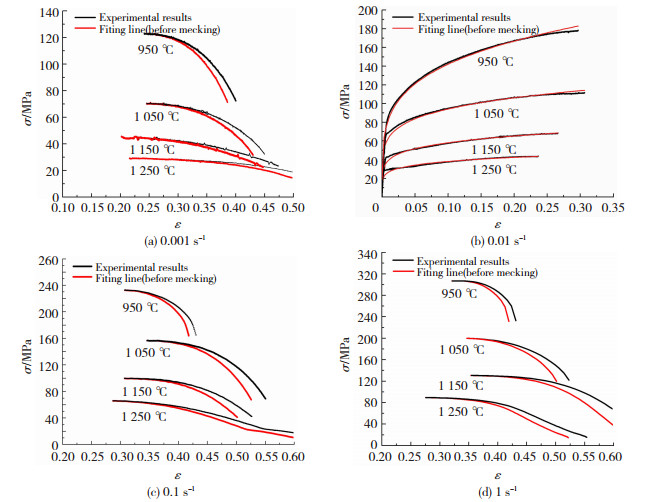
根据式(3)及不同温度不同应变速率下实验测得εN、σEq和εEq,利用直接代入法获得修正的颈缩后应力-应变曲线如图 6所示.由图 6可知:颈缩后应力随应变增加迅速下降,这是因为颈缩发生时材料内部韧窝产生;随着应变的增大,韧窝长大并链接成微裂纹,变形抗力降低[18].
|
图 6 不同应变速率不同温度下颈缩后的真应力真应变实验值与MLR模型预测值 Fig.6 Experimental and obtained values by MLR model of true stress-strain before necking at different strain rates and temperatures |
为验证所修正模型的准确性,将颈缩前与颈缩后的本构模型经Fortran语言编译后嵌入MSC. Marc有限元软件子程序中;同时,输入材料物理常数弹性模量、热膨胀系数、热容系数和导热系数,见表 2~5;泊松比为0.3.利用单元生死法,并选择Oyane判据进行温度为1 050 ℃和应变速率0.1 s-1下拉伸断裂的有限元数值模拟,如图 7所示.
| 表 2 316LN的弹性模量 Table 2 Elasticity modulus of 316LN |
| 表 3 316LN的热膨胀系数 Table 3 Coefficient of thermal expansion of 316LN |
| 表 4 316LN的单位体积热容 Table 4 Heat capacity of 316LN |
| 表 5 316 LN的导热系数 Table 5 Cofficient of thermal conductivity of 316 LN |

|
图 7 316LN颈缩区长度 Fig.7 Neck length of 316LN: (a) finite element simulation; (b) experiment |
由图 7可知,利用有限元模拟的拉伸颈缩区长度与实测值相比,相对偏差为4.73%(由式(4)可得).这说明所建立的高温本构模型(颈缩前与颈缩后两阶段集合本构模型)能够准确描述316LN的高温塑性行为.
| $ 相对偏差=\frac{L-L_{s}}{L}=\frac{21.36-20.35}{21.36} \times 100 \%=4.73 \% $ | (4) |
式中:Ls为颈缩区长度模拟值,L为颈缩区长度实测值.
3 结论1) 通过不同温度不同应变速率下高温拉伸实验,结果表明颈缩发生前真应力-真应变呈幂函数关系,而颈缩发生后,呈非线性函数关系.温度大于950 ℃,断裂应变都大于0.45,且当温度为1 150 ℃,应变速率为1 s-1时,抗拉强度达到了129.95 MPa,断裂应变达到了0.68,这说明在此工况下高温拉伸性能最优.
2) 综合物理实验和数值模拟方法,基于MLR模型修正了拉伸颈缩后真应力应变曲线,并通过Hollomon方程和MLR模型建立了316LN高温拉伸本构模型,模型描述了颈缩发生前与颈缩后的塑变行为;并将有限元模拟的拉伸颈缩区长度与实测值相对比,相对偏差为4.73%.这说明修正后的应力应变关系能够准确描述316LN的高温塑性行为.
| [1] |
VU V D, MIR A, NGUYEN G D, et al. A thermodynamics-based formulation for constitutive modelling using damage mechanics and plasticity theory[J]. Engineering Structures, 2017, 143: 22-39. DOI:10.1016/j.engstruct.2017.04.018 |
| [2] |
CISSE C, ZAKI W, ZINEB T B. A review of constitutive models and modeling techniques for shape memory alloys[J]. International Journal of Plasticity, 2016, 76: 244-284. DOI:10.1016/j.ijplas.2015.08.006 |
| [3] |
LIN Yongcheng, CHEN Xiaomin. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working[J]. Materials and Design, 2011, 32: 1733-1759. DOI:10.1016/j.matdes.2010.11.048 |
| [4] |
JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]//.Den Haag. Proceedings of the 7th International Symposium on Ballistics.The Netherlands: Hugue, 1983: 541-543.
|
| [5] |
VOCE E. The relationship between stress and strain for homogeneous deformation[J]. Journal of the Institute of Metals, 1948, 74: 537-562. |
| [6] |
YANG Xuemei, GUO Hongzhen, LIANG Houquan, et al. Flow behavior and constitutive equation of Ti-6.5Al-2Sn-4Zr-4Mo-1W-0.2Si titanium alloy[J]. Journal of Materials Engineering and Performance, 2016, 25(4): 1347-1359. DOI:10.1007/s11665-016-1963-1 |
| [7] |
ASHTIANI H R R, SHAHSAVARI P. Strain-dependent constitutive equations to predict high temperature flow behavior of AA2030 aluminum alloy[J]. Mechanics of Materials, 2016, 100: 209-218. DOI:10.1016/j.mechmat.2016.06.018 |
| [8] |
GERBIG D, BOWER A, SAVIC V, et al. Coupling digital image correlation and finite element analysis to determine constitutive parameters in necking tensile specimens[J]. International Journal of Solids and Structures, 2016(97-98): 496-509. DOI:10.1016/j.ijsolstr.2016.06.038 |
| [9] |
ZERILLI P J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations[J]. Journal of Applied Physics, 1987, 61: 1816-1825. DOI:10.1063/1.338024 |
| [10] |
PRESTON D L, TONKS D L, WALLACE D C. Model of plastic deformation for extreme loading conditions[J]. Journal of Applied Physics, 2003, 93: 211-220. DOI:10.1063/1.1524706 |
| [11] |
MIRONE G. A new model for the elastoplastic characterization and the stress-strain determination on the necking section of a tensile specimen[J]. International Journal of Solids Structures, 2004, 41(13): 3545-3564. DOI:10.1016/j.ijsolstr.2004.02.011 |
| [12] |
MIRONE G, CORALLO D. A local viewpoint for evaluating the influence of stress triaxiality and lode angle on ductile failure and hardening[J]. International Journal of Plasticity, 2010, 26(3): 348-371. DOI:10.1016/j.ijplas.2009.07.006 |
| [13] |
SAADATKIA S, MIRZADEH H, CABRERA J M. Hot deformation behavior, dynamic recrystallization, and physically-based constitutive modeling of plain carbon steels[J]. Materials Science and Engineering A, 2015, 636: 196-202. DOI:10.1016/j.msea.2015.03.104 |
| [14] |
GUPTA A K, SINGH S K, REDDY S, et al. Prediction of flow stress in dynamic strain aging regime of austenitic stainless steel 316 using artificial neural network[J]. Materials and Design, 2012, 35: 589-595. DOI:10.1016/j.matdes.2011.09.060 |
| [15] |
VALERI G, KOOHBOR B, KIDANE A, et al. Determining the tensile response of materials at high temperature using DIC and the virtual fields method[J]. Optics and Lasers in Engineering, 2017, 91: 53-61. DOI:10.1016/j.optlaseng.2016.11.004 |
 2019, Vol. 27
2019, Vol. 27


