由于内部介质和外部土壤环境的作用,管道易发生局部腐蚀使管壁减薄,从而使得管道修复成为管道工程的一项重要工作[1].在役焊接技术具有带压、不停输的特点,周期短,污染小,费用低,具有广阔的应用前景[2-3].然而,由于焊接电弧热的作用,使得管壁承载能力下降,有发生烧穿的风险[4-5].在役焊接烧穿的本质是,管壁材料在焊接热的作用下受管内介质压力影响而产生的失效损伤过程.由于材料中存在空位、微裂纹等缺陷,严重影响了材料的力学性能,因此,含微缺陷结构服役时的变形过程和失效机理引起了学者们的关注.李本等[6]利用分子动力学方法研究了镍基单晶合金在剪切载荷下的动态演化过程,揭示了温度和剪切应变率对裂纹扩展和微观结构演化的影响.何燕等[7]通过原子模拟钛中的微孔洞结构及其失效行为,揭示了微缺陷能够直接影响材料的物理和力学性能,同时提出空位团簇可以形成层错并对微裂纹的形核产生影响.
由于分子动力学模拟具有沟通宏观特性和微观结构的作用,因此,本文以在役焊接过程中熔池附近不同微区的服役条件为桥梁,采用有限元模拟和分子动力学模拟相结合的方法,研究空位、裂纹等微缺陷对失效过程的影响,从原子层次揭示烧穿失稳的微观机理.
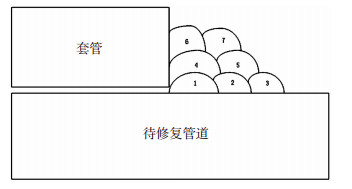
1 在役焊接有限元模拟 1.1 模型建立采用图 1所示的套管修复工艺进行在役焊接过程的数值模拟.由于烧穿一般发生在第1道焊缝[8],因此,研究焊接接头第1道焊缝的温度场、应力场分布.采用1/2管道外壁堆焊模型,如图 2所示.为降低运算量同时保证计算精度,焊缝及高温区网格划分较为稠密,而远离焊缝的区域较为稀疏[9].焊件初始温度为20 ℃,采用的材料为Q235,壁厚4.4 mm.
|
图 1 套管修复工艺示意图 Fig.1 Schematic diagram of sleeve repair process |

|
图 2 管道模型 Fig.2 Pipeline model |
Goldak等[10]提出的双椭球模型能够准确地描述在役焊接过程的热源特性,因此采用双椭球模型进行数值模拟,进行多次热源校核,直至模拟得到的熔池形貌与实际形貌相符,其校核参数如表 1所示, 其中af, ar为前后半椭球长度,b, c为宽度和深度.
| 表 1 热源校核参数 Table 1 Heat source fitting parameters |
管道外表面和空气的换热方式为辐射换热和空气的自然对流换热[11],总换热系数为
| $ \begin{array}{c} \alpha_{外}=0.8 \times 5.67 \times 10^{-8}\left[\left(T+T_{0}\right)\right] \times \\ \left[T_{0}^{2}+T^{2}\right]+25. \end{array} $ | (1) |
式中:T0和T分别为环境温度和焊接接头与空气接触表面的温度.管道内壁和气体间的换热为管内强迫对流换热,其换热系数为
| $ \alpha_{内}=0.027 \frac{\lambda}{d} R e^{0.8} P r^{1 / 3}\left(\frac{\mu}{\mu_{w}}\right)^{0.14}. $ | (2) |
式中:λ、Re、Pr、μ分别为气体的导热系数、雷诺数、普朗特数、动力粘度;d为管道的内径;μw为气体在室温时的动力粘度.
| $ \mu_{w}=\mu_{0}\left(\frac{273.15+T_{1}}{273.15}\right)^{0.76}. $ | (3) |
式中:T1为管道内壁的温度,μ0为气体0 ℃时的动力粘度.此外,模型两端的力学约束采用刚性约束.
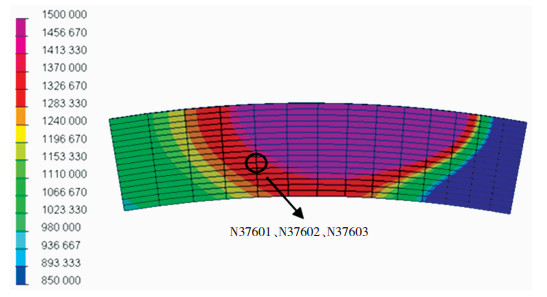
1.3 温度场和应力场计算结果与分析对在役焊接过程进行有限元数值模拟,得到焊接电弧经过该截面时(10.24 s)熔池附近区域的温度场分布,如图 3所示.
|
图 3 熔池区域的温度场分布 Fig.3 Temperature distribution around molten pool |
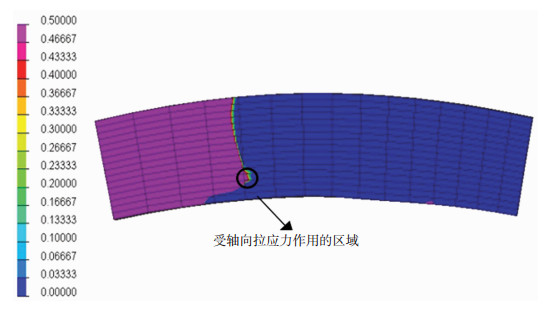
对于环焊缝,轴向应力是引起损伤失效的主要因素,图 4给出了熔池附近区域的轴向应力分布.由图 4可以看出,焊接电弧经过时,熔深最大处下方管壁的轴向应力表现为压应力,而其后方表现为拉应力,如图 4红色区域所示,因而烧穿更容易发生在熔深最大处后方.选取如图所示的节点,得到其瞬时的温度、应变率大小.所选取的网格节点从熔合线附近往下依次标记为N37601、N37602、N37603.
|
图 4 熔池区域的轴向应力分布 Fig.4 Axial stress distribution around molten pool area |
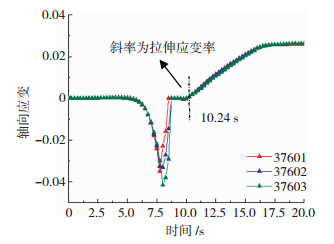
图 5和图 6分别给出了所选取网格节点的温度、轴向应变随时间的变化曲线.在焊接电弧经过该截面时(10.24 s),各节点的温度及拉伸应变率即为管壁材料此刻的服役条件,其具体大小如表 2所示.本文以各节点的服役条件作为沟通宏观、微观模拟的桥梁,进而从原子水平研究烧穿失稳的动态演化过程.

|
图 5 各节点的温度变化曲线 Fig.5 Temperature curves of selected nodes |
|
图 6 各节点的轴向应变变化曲线 Fig.6 Axial strain curves of selected nodes |
| 表 2 各节点在10.24 s时的温度与轴向应变率大小 Table 2 Temperature and axial strain rate of each node at 10.24 s |
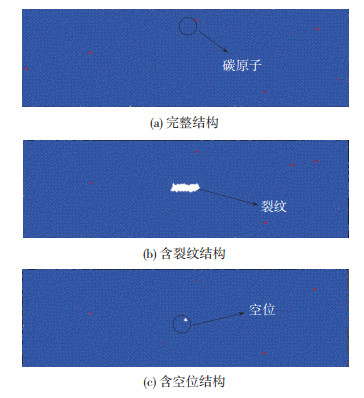
采用大型分子动力学计算软件LAMMPS[12]进行建模与模拟计算.为更直观地模拟材料失效过程中原子结构的动态演化过程,同时减少运算量,建立二维Fe-C合金模型,在X方向排列100个原子层,在Z方向上排列30个原子层.为研究微缺陷对材料力学性能的影响,分别建立完整合金结构、含裂纹结构、含空位结构,如图 7所示.
|
图 7 初始合金结构 Fig.7 Initial structure of alloy: (a)intact structure; (b)cracked structure; (c)vacancy structure |
以在役焊接接头不同微区的温度、应力状态作为分子动力学模拟的初始条件.首先,建模完成后,利用共轭梯度法对初始结构进行能量最小化处理,使得体系中原子按照能量最低状态分布;再利用速度标定法控制体系在指定的温度(1 536/1 519/1 501 K),使原子速度满足特定温度条件下的高斯分布,弛豫过程的加载时间步为10万步,时间积分步长取为0.001 ps.模拟过程中采用周期性边界条件,以减少体系粒子数小于真实系统粒子数而带来的表面效应.
同时,本文参考Hepburn和Ackland[13]提出的镶嵌原子势函数来描述原子之间的相互作用.在正则系综下,以所选取网格节点的瞬时应变率为加载条件,在X方向上对称地施加拉伸载荷,来模拟材料失效的过程.加载过程持续30万个时间步,每1 000步输出原子的坐标、势能、应力等.
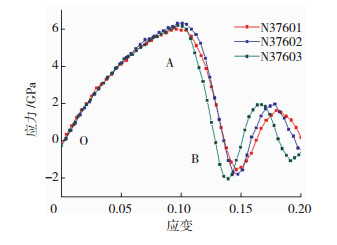
3 结果分析 3.1 力学性能分析图 8给出了N37601、N37602、N37603微区在高温下受拉伸载荷作用的应力-应变曲线,可将其分为3个阶段.第1阶段(OA)为线弹性变形阶段.随着应变的增加,应力急剧上升.当应力达到5.98 GPa时,N37601发生屈服,而对于N37602和N37603,其弹性极限均大于N37601.因此,靠近熔合线的微区强度较低,其力学性能较差.第2阶段(AB)为金属键断裂阶段.随着应变的增加,体系中部分金属键断裂,应力得到一定程度释放,从而应力急剧下降.第3阶段(B点以后),材料进入塑性变形阶段,随着应变进一步增加,原子间不断发生旧的金属键断裂和新的金属键生成,应力-应变曲线在一定范围内波动.波谷上升对应位错发射到表面的过程,而波峰下降对应于位错滑移面产生的过程.
|
图 8 各微区的应力-应变曲线 Fig.8 Stress-strain curves of each microregion |
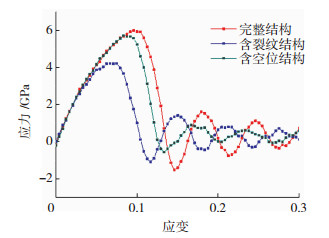
图 9为完整结构和含缺陷结构的应力-应变曲线.当应力达到4.2 GPa时,含裂纹结构达到弹性极限,对应的临界应变为6.7%,当应力达到5.7 GPa时,含空位结构发生屈服.而对于完整结构,当应力达到5.98 GPa时才发生屈服.随后材料进入塑性变形阶段,应力皆上下波动,曲线呈锯齿状.由于微缺陷的影响,材料的强度明显降低,而对塑性变形阶段的影响较小.
|
图 9 完整结构和含缺陷结构的应力-应变曲线 Fig.9 Stress-strain curves of intact structure and defective structure |
微观结构分析方法中,中心对称参数法能够很好地预测结构中存在的各种微缺陷,如孔洞、位错等[14],因此,本文采用中心对称参数法来研究失效过程中原子微观结构的动态演化过程.图 10~12分别给出了完整结构、含裂纹结构、含空位结构在几个典型时间步的中心对称参数分布、轴向应力分布以及体应变分布.分别用渐变色谱来表征中心对称参数、应力、应变的大小,其数值由小到大表现为由深蓝色到深红色的连续变化.当原子结构规则稳定时,中心对称参数值较小,表现为深蓝色.当原子结构遭到破坏时,中心对称参数变大,表现为绿色或红色,且数值越大颜色越鲜艳.

|
图 10 完整结构的微观结构变化图 Fig.10 Microstructural diagram of intact structure: (a) centrosymmetric parameter distribution; (b) stress distribution; (c) strain distribution |

|
图 11 含裂纹结构的微观结构变化图 Fig.11 Microstructural diagram of cracked structure: (a) centrosymmetric parameter distribution; (b) stress distribution; (c) strain distribution |
|
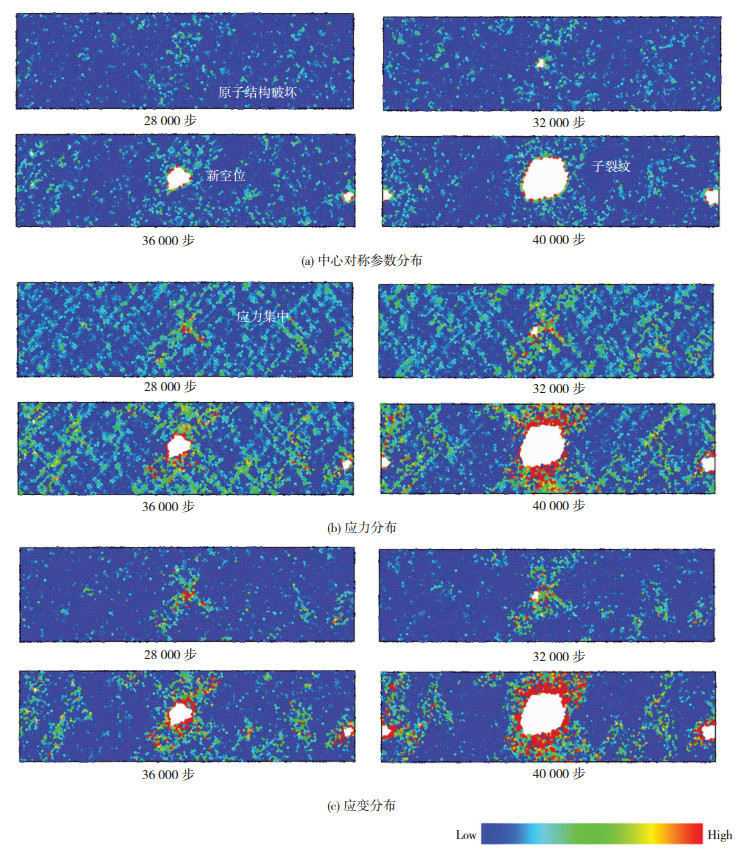
图 12 含空位结构的微观结构变化图 Fig.12 Microstructural diagram of vacancy structure: (a) centrosymmetric parameter distribution; (b) stress distribution; (c) strain distribution |
图 10给出了完整结构在拉伸失效的过程中的微观结构演化图.在22 000步时,在应力集中作用下,材料发生塑性变形,原子结构遭到破坏.随着加载过程中原子不断移动,原子间的相互作用遭到破坏,金属键断裂.到34 000步时,体系中出现空位等微缺陷结构.同时,在微缺陷形核处,原子应变较大,出现应力集中区域,与拉伸方向呈45°.由于拉伸载荷的持续作用,原子间隙不断增大,塑性变形加剧,空位发展成为裂纹.随后裂纹扩展,贯穿整个体系,导致结构失效.
图 11给出了含中心裂纹结构在拉伸过程的结构演化图.加载初期,裂纹面被拉开,但尚未发生裂纹的扩展,如22 000步的微观结构图所示,而在裂纹尖端出现了明显的应力集中区域.随着塑性变形加剧,裂尖区域原子间的相互作用无法抵消应力的作用,使得原子间金属键断裂,进而发生裂纹的扩展.由于拉伸载荷的持续作用,应力集中区域扩大,裂纹继续沿着滑移面发生塑性变形,到34 000步时,体系中形成贯穿性裂纹,最终结构失效.
而对于含空位的结构,如图 12所示,加载初期,空位周围应力集中,材料发生塑性变形,原子结构遭到破坏.随着时间步的推移,应变能积累,空位沿着{110}滑移面扩展,同时萌生新的空位.到40 000步时,结构的塑性变形增加到一定程度,形成贯穿整个体系的主裂纹,最终导致结构失效.裂纹、空位等微缺陷存在,大大加速了体系失效破坏的进程.
由分子动力学模拟结果可知,烧穿是由于高温和拉伸载荷的共同作用而导致结构失效的过程.管壁材料的失效经历了微缺陷的形核、积累及扩展.微缺陷的存在,降低了结构的稳定性,在应力集中的作用下,体系在缺陷处起裂,大大加速了结构破坏的进程.
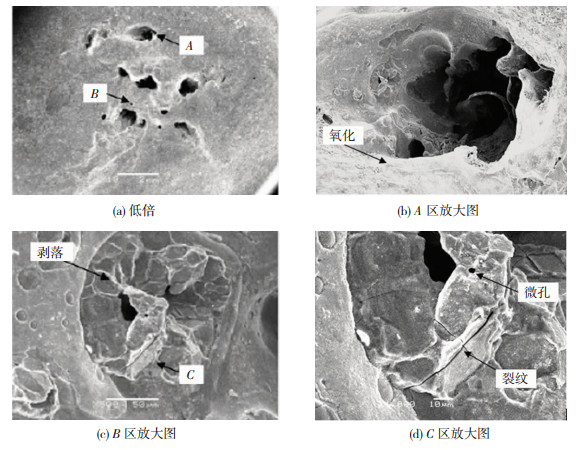
郭广飞等[15]对在役焊接烧穿失稳形貌分析发现,失效区存在纵横交错的微裂纹、微孔及明显的氧化痕迹,如图 13所示.因此,在役焊接烧穿失稳的本质,是在焊接热和内压作用下,微观结构发生永久性损伤,微裂纹和微孔洞等缺陷成核、扩展,形成贯穿性主裂纹,进而导致了宏观裂纹的形成与扩展,最终结构失稳或完全破坏导致烧穿.实验结果在一定程度上反映了模拟结果的可靠性,同时,分子动力学模拟的结果也进一步揭示了材料失效过程中原子层次的动力学行为,为烧穿机理的研究提供了科学的理论支撑.
|
图 13 在役焊接烧穿失稳微观形貌[17] Fig.13 Microscopic morphology of burn-through[17]: (a) low magnification; (b) enlargement of A; (c) enlargement of B; (d) enlargement of C |
1) 在役焊接烧穿是由于高温和拉伸载荷共同作用而导致的失效过程.焊接电弧经过时,烧穿失稳更易发生在熔深最大处后方.熔池下方的各微区中,熔合线附近力学性能较差,在焊接热和应力的作用下最先失效.
2) 微缺陷结构显著降低了管壁材料的强度,而对于材料的塑性影响不大.
3) 在役焊接烧穿是一个宏、微观结合的多层次过程,其本质是大量微观层次的微缺陷成核、长大、积累、连接最终导致宏观失效的过程.含微缺陷的管壁材料,在应力集中的作用下沿缺陷处起裂,大大降低了材料结构的稳定性,加快了失效的进程.
| [1] |
FARZADI A. Gas pipeline failure caused by in-service welding[J]. Journal of Pressure Vessel Technology, 2016, 138(1): 1-9. |
| [2] |
谷云龙, 丁雅萍, 袁代英, 等. 焊接顺序对管道在役焊接温度和应力场的影响[J]. 压力容器, 2018, 35(3): 44-50. GU Yunlong, DING Yaping, YUAN Daiying, et al. Effect of welding sequence on in-service welding temperature and stress field of natural gas pipeline[J]. Pressure Vessel Technology, 2018, 35(3): 44-50. DOI:10.3969/j.issn.1001-4837.2018.03.008 |
| [3] |
付威, 吕宇玲. 油气管道在役焊接修复技术综述[J]. 热加工工艺, 2017, 46(19): 15-18. FU Wei, LYU Yuling. Overview of in-service welding repair technology for oil and gas pipelines[J]. Hot Working Technology, 2017, 46(19): 15-18. DOI:10.14158/j.cnki.1001-3814.2017.19.004 |
| [4] |
俞树荣, 李建华, 李淑欣, 等. 埋地管道腐蚀剩余寿命预测概率模型[J]. 中国安全科学学报, 2008, 18(6): 11-15. YU Shurong, LI Jianhua, LI Shuxin, et al. Probability model for the prediction of corrosion remaining life of underground pipelines[J]. China Safety Science Journal, 2008, 18(6): 11-15. DOI:10.3969/j.issn.1003-3033.2008.06.002 |
| [5] |
郭广飞, 王勇, 韩涛. X70钢高压输气管线在役焊接剩余强度尺寸效应数值模拟[J]. 焊接学报, 2016, 37(9): 110-114. GUO Guangfei, WANG Yong, HAN Tao. Numerical simulation of residual strength size effect of X70 steel high pressure gas pipeline in-service welding[J]. Transactions of the China Welding Institution, 2016, 37(9): 110-114. |
| [6] |
李本, 张世明, ESSA F A, 等. 剪切载荷条件下镍基单晶合金裂纹扩展与微观结构演化行为研究[J]. 稀有金属材料与工程, 2018, 47(5): 1370-1376. LI Ben, ZHANG Shiming, ESSA F A, et al. Crack propagation and microstructural evolution of Ni-based single crystal alloy under shear loads[J]. Rare Metal Materials & Engineering, 2018, 47(5): 1370-1376. |
| [7] |
何燕, 刘艳侠, 王皞, 等. 原子模拟钛中微孔洞的结构及其失效行为[J]. 物理学报, 2018, 67(5): 27-33. HE Yan, LIU Yanxia, WANG Hao, et al. Atomistic simulation of microvoid formation and its influence on crack nucleation in hexagonal titanium[J]. Acta Physica Sinica, 2018, 67(5): 27-33. DOI:10.7498/aps.20171670 |
| [8] |
HUANG Z, TANG H, DING Y, et al. Numerical simulations of temperature for the in-service welding of gas pipeline[J]. Journal of Materials Processing Technology, 2017, 248: 72-78. DOI:10.1016/j.jmatprotec.2017.05.008 |
| [9] |
王勇, 孙启平, 韩涛, 等. 基于等效缺陷尺寸在役焊接安全性评价研究[J]. 中国石油大学学报(自然科学版), 2017, 41(1): 124-129. WANG Yong, SUN Qiping, HAN Tao, et al. Safety evaluation of service welding based on equivalent defect size[J]. Journal of China University of Petroleum(Edition of Natural Sciences), 2017, 41(1): 124-129. DOI:10.3969/j.issn.1673-5005.2017.01.016 |
| [10] |
JOHN G, ADITYA C, MALCOLM B. A new finite element model for welding heat sources[J]. Metallurgical Transactions B, 1984, 15(2): 299-305. DOI:10.1007/BF02667333 |
| [11] |
陈玉华, 王勇. 基于SYSWELD的运行管道在役焊接热循环数值模拟[J]. 焊接学报, 2007, 28(1): 85-88. CHEN Yuhua, WANG Yong. Numerical simulation of thermal cycle of in-service welding onto active pipeline based on SYSWELD[J]. Transactions of the China Welding Institution, 2007, 28(1): 85-88. DOI:10.3321/j.issn:0253-360X.2007.01.022 |
| [12] |
PLIMPTON S J. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19. |
| [13] |
HEPBURN D J, ACKLAND G J. Metallic-covalent interatomic potential for carbon in iron[J]. Physical Review B, 2008, 78(16): 1-6. |
| [14] |
郭永博, 梁迎春. 单晶铜纳米加工过程中热效应及缺陷结构的原子尺度模拟[J]. 中国有色金属学报(英文版), 2012, 22(11): 2762-2770. GUO Yongbo, LIANG Yingchun. Atomistic simulation of thermal effects and defect structures during nanomachining of copper[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(11): 2762-2770. |
| [15] |
郭广飞, 王勇, 黎超文, 等. 压力管道在役焊接烧穿失稳机制[J]. 材料科学与工艺, 2012, 20(3): 62-66. GUO Guangfei, WANG Yong, LI Chaowen, et al. Burn-through failure mechanism of in-service welding of pipeline[J]. Materials Science and Technology, 2012, 20(3): 62-66. |
 2019, Vol. 27
2019, Vol. 27


