2. 中国科学院金属研究所 非平衡金属材料研究部,沈阳 110016;
3. 辽宁石油化工大学 机械工程学院,辽宁 抚顺 113001
2. Unbalanced Metal Materials Research Department, Institute of Metal Research Chinese Academy of Sciences, Shenyang 110016, China;
3. School of Mechanical Engineering, Liaoning Shihua University, Fushun 113001, China
与传统金属材料相比,非晶材料具有完全不同的结构:原子排列长程无序、短程有序,表现出很多优良的材料性能,非常适合应用于涂层领域来保护基体材料[1-4]。目前,超音速火焰喷涂技术(HVOF)制备的Fe基非晶涂层以其相对低的成本和高性能而备受青睐,得到比较的广泛应用[5-6]。
涂层的孔隙率是评价涂层质量的重要性能指标。在不同喷涂工艺参数的影响下,喷涂粒子在喷涂过程中的物理化学状态有很大差别,因此,有些工艺参数难以保证涂层质量[7-8]。研究发现[9-11],喷涂距离是影响涂层孔隙形成的重要工艺参数。在热喷涂过程中,颗粒由枪管喷出,颗粒自身温度和速度发生剧烈变化。因此,颗粒撞击基板时的温度和速度,会直接影响涂层内部孔隙的数量及分布,进而影响涂层的质量。文献[12]的研究表明,当HVOF喷涂粉末的温度靠近粉末熔点,喷涂速度稍低时会形成高致密度的涂层,这成为研究喷涂工艺,制备高质量涂层的一个标准参照。综合上述研究成果,本文采用数值模拟与设计验证实验分析相结合的方式,对使用JP-8000型超音速火焰喷涂系统制备SAM2X5 Fe基非晶涂层(Fe49.7Cr18Mn1.9Mo7.4W1.6B15.2C3.8Si2.4,at.%),分析喷涂距离对非晶涂层内孔隙率的影响规律,寻找最佳的喷涂距离范围,以降低涂层内部的孔隙率,提高涂层质量。
1 有限元模型及实验 1.1 计算机流体力学(CFD)模型根据现有的计算模型,使用商用有限元计算软件Fluent,对喷涂过程的物理模型进行改进(图 1),增加了基板,便于更精确的模拟计算出颗粒整个飞行过程中的温度和速度变化。JP-8000煤油-氧气热喷涂系统喷枪的(Praxair, US)二维计算机计算网格模型如图 1所示,整个计算域由煤油-氧气的燃烧室,收敛汇聚的拉瓦尔喷嘴区、枪管区和自由喷射区域4个部分组成。为了使有限元数值计算结果更为准确,对拉瓦尔喷嘴和枪管区域进行了细化处理。

|
图 1 JP-8000喷枪有限元计算机模型 Fig.1 Finite element computer model of JP-8000 spray gun |
HVOF数值计算的CFD(计算机流体力学)模型主要包含流体模型、燃烧模型和离散相模型。
对于流体模型,通过分析喷涂过程和文献调研,得出喷涂火焰属于圆形枪管向外喷射的湍流可压缩流动,因此,选择能够精确预测平面和圆形射流扩散流动的可实现(Realizable)k-ε湍流模型,其二维控制方程如下[13]。
质量守恒方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = {S_{\text{m}}}, $ | (1) |
式中:ρ为流体密度;ui为流体速度;Sm是源项,为稀疏相添加到连续相中的质量,如液体蒸发变成气体等情况。
动量守恒方程:
| $ \begin{array}{l} \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial \rho }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}{\left( {{T_{ij}}} \right)_{{\rm{eff }}}} + \\ \frac{\partial }{{\partial {x_j}}}\left( { - \rho u_i^\prime u_j^\prime } \right). \end{array} $ | (2) |
式中:p为静压;τij为应力张量。
能量守恒方程:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}(\rho E) + \frac{\partial }{{\partial {x_i}}}\left[ {{u_i}(\rho E + p)} \right] = \\ \frac{\partial }{{\partial {x_j}}}\left( {{k_{{\rm{eff }}}}\frac{{\partial t}}{{\partial {x_i}}} + {u_i}{{\left( {{T_{ij}}} \right)}_{eff}}} \right) + {S_{\rm{h}}}, \end{array} $ | (3) |
| $ {\left( {{T_{ij}}} \right)_{{\rm{eff}}}} = {\mu _{{\rm{eff}}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_i}}} + \frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) - \frac{2}{3}{\mu _{{\rm{eff}}}}\frac{{\partial {u_i}}}{{\partial {x_i}}}{\delta _{ij}}. $ | (4) |
式中:keff为有效导热系数;Sh是包括化学反应热和其他体积热源的源项。
对于燃烧模型,JP-8000型HVOF喷涂系统的燃料为煤油和氧气,二者在燃烧室内充分混合并发生剧烈的化学反应——燃烧,产生高温高压火焰。煤油燃料是烷烃(CnH2n + 2)的混合物,其中碳数在9~17。因此,这种液体燃料没有确切的化学式。本文令C12H26用作煤油各个组分的代表性平均值。燃烧动力学由一个全局反应方案表示,用来描述燃烧室中的解离和中间反应。
| $ \begin{array}{l} {n_1}{{\rm{C}}_{12}}{{\rm{H}}_{26}} + {n_2}{{\rm{O}}_2} \to {n_3}{\rm{C}}{{\rm{O}}_2} + {n_4}{\rm{CO}} + {n_5}{{\rm{H}}_2}{\rm{O}} + \\ {n_6}{\rm{OH}} + {n_7}{{\rm{O}}_2} + {n_8}{\rm{O}} + {n_9}{{\rm{H}}_2} + {n_{10}}{\rm{H}}{\rm{.}} \end{array} $ | (5) |
式(5)中的系数n由燃烧室压力、燃料与氧气比率、质量流率或火焰几何形状等变量决定。为求得不同情况的反应系数,本文采用基于化学平衡模型的迭代方法——涡流耗散模型[14-15],该方法的解为基于物种质量分数的输运方程的解。通过这种方法确保求得的全局反应结果代表正确的压力水平和热流场。该方法假设反应速率由湍流控制,而不是Arrhenius化学动力学的计算。反应r中物种i的净生产率Ri, r由下面两个等式中较小的一个给出。
| $ {R_{i, r}} = {v_{i, r}}{M_{w, i}}A\rho \frac{\varepsilon }{k}\min \left( {\frac{{{Y_R}}}{{{v_{R, r}}{M_{\omega , R}}}}} \right), $ | (6) |
| $ {R_{i, r}} = {v_{i, r}}{M_{w, i}}AB\rho \frac{\varepsilon }{k}\left( {\frac{{\sum\nolimits_P {{Y_P}} }}{{\sum\nolimits_J^N {v_{j, r}^\prime } {M_{w, j}}}}} \right). $ | (7) |
式中:YR为反应物R的质量分数;YP为燃烧产物中组分为P的质量分数;经验常数A=4,B=0.5;vi, r为反应r中反应物i的化学计量系数;Mω, i为反应物i的分子量;Mω, R为反应物R的分子量;Mω, j为反应物j的分子量。
对于离散相模型(Discrete Phase Mode, DPM),根据喷枪结构,在拉瓦尔喷嘴末端之后一定距离注入喷涂粉末,此时喷枪内部流场包含两相,分别为连续的气体相和不连续的粉末颗粒相,因此选用Navier-Stokes方程,不仅计算进出气相的热量和质量传递,还计算这些离散相实体的轨迹,包括力平衡方程和能量方程[16-17]。
力平衡方程,描述粒子在x方向上的运动方程(使用笛卡尔坐标)可以描述为颗粒惯性力与作用在粒子上的力的力平衡方程,表达式为
| $ \frac{{{\rm{d}}{u_{\rm{P}}}}}{{{\rm{d}}t}} = \frac{{18u}}{{{\rho _{\rm{P}}}d_{\rm{P}}^2}}\frac{{{C_D}}}{{24}}\left( {u - {u_{\rm{P}}}} \right) + {F_x}. $ | (8) |
忽略通过热辐射传递的能量,能量方程为
| $ {m_{\rm{P}}}{c_{\rm{P}}}\frac{{{\rm{d}}{T_{\rm{P}}}}}{{{\rm{d}}t}} = h{A_{\rm{P}}}\left( {{T_g} - {T_{\rm{P}}}} \right). $ | (9) |
式中:u为连续相速度;uP为颗粒速度;AP为颗粒表面积;CD为阻力系数;cP为比热;ρP为流体的密度;dP为颗粒直径;mP为颗粒质量。
1.1.2 边界条件将工厂实际喷涂生产的经验工艺参数,如煤油流量、氧气流量和氮气流量等用作数值计算初始边界条件,见表 1。SAM2X5 Fe基非晶粉末用作喷涂粉末,实验测得其热物理性参数见表 2。
| 表 1 JP-8000超音速火焰喷涂系统喷涂工艺条件 Table 1 Spraying parameters of JP-8000 high velocity oxygen flame spraying system |
| 表 2 SAM2X5铁基非晶粉末热物理性能参数 Table 2 Thermophysical properties of SAM2X5 iron-based amorphous powder |
根据SAM2X5非晶粉末成分配比原材料,使用真空电弧炉熔炼成母材,用真空铜模吸铸法制备非晶条带,铜轮转速40 m/s。利用粉末真密度测试仪测得粉末密度。由DSC Q2000型差示扫描量热仪,使用MDSC调试法测得比热。导热系数由DXF500型氙灯导热仪测得。固相线和液相线温度采用高温DSC测得,样品质量10 mg,实验样品和标样的测量均采用Al2O3坩埚,氩气保护,升温速率为20 ℃/min。选用304不锈钢板(100 mm×40 mm×5 mm)作为基底,用JP-8000超音速火焰喷涂系统制备Fe基非晶粉末涂层。实验前对基体进行喷砂处理,粉末粒径和喷涂工艺条件如表 1所示。采用X射线衍射仪(Rigaku D / max 2400,单色Cu Kα射线源(λ=0.1542 nm),扫描速度4°/min,对SAM2X5 Fe基非晶粉末、所制备涂层和条带进行检测。使用扫描电子显微镜Quanta 600对涂层表面和截面的微观组织和形貌进行分析,选取不同喷涂距离下,涂层的多个(5个)局部位置,进行涂层截面SEM观察,通过Image-Pro-Plus软件进行孔隙率计算。
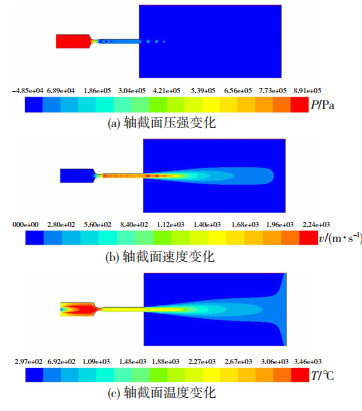
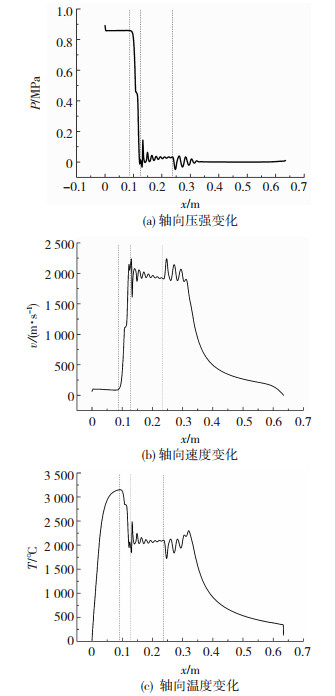
2 结果与讨论图 2(a),(b),(c)展示了加入喷涂粉末之前,采用CFD方法模拟计算的喷涂过程中火焰流场的压强(p)、速度(v)和(T)温度分布云图。液态煤油和氧气注入燃烧室中,经化学反应后转化为高温高压的气体。燃烧室中的气体速度较低,在收敛-扩散的拉瓦尔喷嘴中其急剧加速,产生超音速火焰流。图 3(a),(b),(c)显示了模型轴向的压强、速度和温度变化曲线,图中虚线将曲线分为4个部分,从左到右依次代表燃烧室、拉瓦尔喷嘴、枪管和空气域。
|
图 2 气体流场云图 Fig.2 Gas flow field map:(a) pressure change of axial cross section; (b) velocity change of axial cross section; (c) temperature change of axial cross section |
|
图 3 气体流场轴向变化曲线 Fig.3 Axial flow curve of gas flow field:(a) axial pressure change; (b) axial velocity change; (c) axial temperature change |
如图 3(a)所示燃烧室中的气体压力约为0.8~ 0.9 MPa,在枪管内的气体压力低于0.1 MPa,但在枪管出口附近有所波动。图 3(b)显示了相对于轴向距离绘制的中心线轴向上的气体速度。总体趋势是在拉瓦尔喷嘴的汇聚部分速度急剧增加,在枪管内火焰速度几乎保持一致,略有降低趋势,枪管内的速度为1 800~2 000 m/s。在枪管的出口处,由于膨胀-压缩波在喷管口外部急剧变化,火焰速度不断增加和减少,在空气域的轴线上出现4次马赫锥后经历缓慢衰减。喷枪出口处火焰压力的波动是由火焰周期性地过度膨胀产生的,然后在大气压力之上和之下重新收敛。气体温度的一般趋势(图 3(c))是在拉瓦尔喷嘴前急剧增加,并沿喷嘴长度急剧减小,在枪管内火焰温度几乎保持一致。值得注意的是,中心线上,最高温度为3 100 ℃左右。在喷枪出口处,温度为1 900~2 200 ℃,而后随喷涂距离急剧降低。
图 4和图 5为使用DPM模型计算加入非晶粉末颗粒后,不同喷涂距离下颗粒速度和温度的变化曲线。图中的虚线表示枪管出口位置,将颗粒飞行的温度和速度变化曲线分成喷枪内部和喷枪外部两个部分。由图 4和图 5可以看到,不同喷涂距离下,在喷枪内部,喷涂粒子的速度和温度急剧升高。喷枪管口处,5~45 μm的颗粒速度为300~1 100 m/s,温度为950~2 500 ℃,而后颗粒进入马赫锥部分进行缓慢的加热和加速,速度和温度分别到达最大值,随后在空气中降温降速,最后撞击基板冷却形成涂层。将不同粒径粉末在不同喷涂距离下颗粒撞击基板时的速度统计为图 4(d)。在图 4(d)中可以明显看到,当颗粒直径处于5~20 μm范围时,同一喷涂距离下,颗粒撞击基板时降温降速剧烈,工艺不容易控制,不适合作为制备涂层的粒径范围。当颗粒直径处于20~40 μm范围时,不同喷涂距离下,在撞击基板时,相同粒径的粉末颗粒撞击速度近似一致,说明喷涂距离对此粒径范围内颗粒的撞击速度影响不大。

|
图 4 粉末颗粒在气体流场中的速度变化曲线 Fig.4 Velocity curve of powder particle velocity in gas flow field |
|
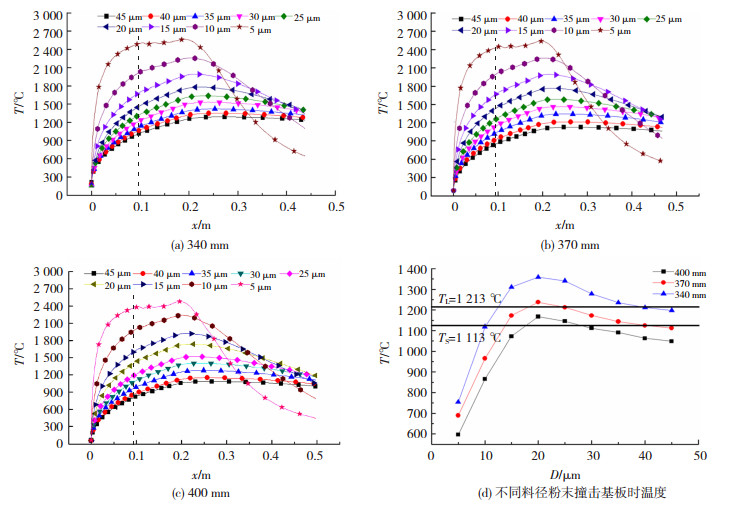
图 5 粉末颗粒在气体流场中的温度变化曲线 Fig.5 Temperature curve of powder particles in gas flow field |
图 5中的(a),(b),(c)分别是喷涂距离为340,370,400 mm时不同粒径颗粒的温度变化曲线,可以看到,不同粒径颗粒在喷涂过程中温度变化趋势一致,颗粒温度均为在喷枪内速度迅速升高,喷出喷枪后,在距离枪管口一定距离内温度缓慢上升,之后颗粒在空气中飞行,温度缓慢降低。值得注意的是,在颗粒撞击涂层之前的一小段距离,颗粒的温度降低幅度最低,这是因为基板对高温的火焰气流具有阻挡作用,气流撞击基板后折向两侧,在基板表面附近形成了一层保温层,颗粒进入保温层自身的温度降低减慢。将不同喷涂距离下颗粒撞击时温度整理为图 5(d),根据文献[12],颗粒沉积温度处于材料液相线和固相线之间的这种半固态状态时,颗粒的流动性最好,且能取得优质涂层。由图 5(d)可知,当喷涂距离为370 mm时,颗粒处于固液相线之间的点最多,为此本文提出,当喷涂距离处于360~380 mm范围内可获得优质涂层。
综合图 4(d)和图 5(d),相同喷涂距离条件下,5~20 μm范围内的颗粒撞击速度高,但粒子已经处于固态,不适合制备涂层。而不同喷涂距离条件下,粒径在20~40 μm范围内的颗粒撞击时速度差异不明显,颗粒撞击速度相对较高,能够形成致密涂层[19],且当喷涂距离为370 mm时,粒径在20~40 μm范围内,颗粒处于固液相线之间的点最多,此状态下制得涂层质量会更好。因此,本文认为:HVOF喷涂Fe基非晶粉末的粒径范围为20~40 μm时熔化状态最稳定;HVOF喷涂Fe基非晶涂层的最佳喷涂距离为360~380 mm。
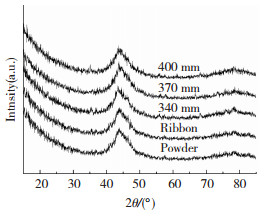
为验证数值模拟结果的准确性,采用图 6所示Fe基非晶粉末(20~40 μm)制备了Fe基非晶涂层,可以看出,大部分粉末颗粒是球形或接近球形的,尽管一些颗粒附着一些更小的颗粒,但大多数颗粒表现出光滑的表面,使其在喷涂过程中具有良好流动性。Fe基非晶粉末、条带和喷涂沉积涂层的XRD谱图见图 7,其中漫射图案表现出无任何与结晶相相关的晶化峰,表明它们是完全非晶的。

|
图 6 2X5Fe基非晶粉末 Fig.6 SAM2X5 Fe-based amorphous powder |
|
图 7 X射线衍射谱图 Fig.7 X-ray diffraction spectrum |
不同喷涂距离所制备的Fe基非晶涂层的表面形态(左侧)和截面形貌(右侧)如图 8所示。表面形态显示,喷涂距离为370 mm时,涂层表面光亮、致密,无未熔化颗粒,且截面孔隙少,证明粉末粒子处于半固态时,在基板上具有很好的流动性;喷涂距离为340 mm时,涂层表面与喷涂距离为370 mm所制备涂层表面相似,涂层表面无未熔化的颗粒,但涂层表面孔隙较多,这是因为粉末颗粒完全熔化,撞击基板时,急剧铺展并发生飞溅,容易产生孔隙,涂层截面层间的孔隙正是飞溅的堆积产生的;当喷涂距离为400 mm时,可以明显发现涂层表面存在未熔化的固态颗粒,当这些固态颗粒存在于前一层上,后一层的粉末会包裹在这些颗粒周围,并在这些未熔化颗粒周围形成孔隙,涂层截面形貌也证明了这一结论。

|
图 8 不同喷涂距离涂层样品表面和截面SEM形貌 Fig.8 SEM topography of the surface and cross section of the coating sample at different spraying distances |
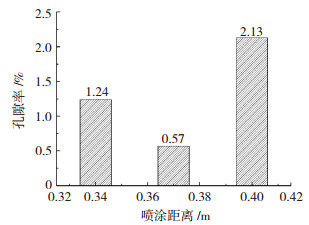
把Image-Pro-Plus软件计算的孔隙率结果进行数学处理,得出孔隙率平均值及其标准方差,见表 3。将非晶涂层孔隙率平均值制成图 9所示的柱状图。据表 3和图 9可知,喷涂距离为370 mm的涂层平均孔隙率为0.57%,孔隙率最低,且标准偏差最小,为0.1574%,处于可接受范围。故可以得出,随着喷涂距离的增加,从340~400 mm,涂层的孔隙率先降低后增加,喷涂距离大于400 mm后,喷涂距离越大孔隙率越高,验证了最佳喷涂距离范围。
| 表 3 Fe基非晶涂层孔隙率统计结果 Table 3 Statistical results of porosity of Fe-based amorphous coatings % |
|
图 9 不同喷涂距离涂层样品截面孔隙率 Fig.9 Cross-sectional porosity of coated samples at different spray distances |
1) 模拟结果表明,喷涂距离处于360~380 mm,非晶粉末颗粒在冲击基板时处于半融化状态,且冲击速度较高,颗粒在基板上具有良好的流动性,可取得优质涂层。
2) 验证实验结果表明,喷涂距离为370 mm时,涂层的孔隙率最低,为0.57%,验证了最佳喷涂距离范围。
3) 喷涂距离由340 mm增加到400 mm,涂层的孔隙率由高变低再增高,当喷涂距离处于360~380 mm范围内,Fe基非晶涂层孔隙率最低,涂层质量最好。
| [1] |
SHI M, PANG S, ZHANG T. Towards improved integrated properties in FeCrPCB bulk metallic glasses by Cr addition[J]. Intermetallics, 2015, 61: 16-20. DOI:10.1016/j.intermet.2015.02.010 |
| [2] |
MA H R, CHEN X Y, LI J W, et al. Fe-based amorphous coating with high corrosion and wear resistance[J]. Surface Engineering, 2016, 33(1): 56-62. DOI:10.1080/02670844.2016.1176718 |
| [3] |
ZHOU J, WALLESER J K, MEACHAM B E, et al. Novel in situ transformable coating for elevated-temperature applications[J]. Journal of Thermal Spray Technology, 2010, 19(5): 950-957. DOI:10.1007/s11666-010-9498-8 |
| [4] |
KUMAR P, SIDHU B S. Characterization and high-temperature erosion behavior of HVOF thermal spray cermet coatings[J]. Journal of Materials Engineering & Performance, 2015, 25(1): 1-9. DOI:10.1007/s11665-015-1818-1 |
| [5] |
ZHOU Z, WANG L, WANG F C, et al. Formation and corrosion behavior of Fe-based amorphous metallic coatings by HVOF thermal spraying[J]. Surface & Coatings Technology, 2009, 204(5): 563-570. DOI:10.1016/j.surfcoat.2009.08.025 |
| [6] |
ZHOU Z, WANG L, HE D Y, et al. Microstructure and wear resistance of Fe-based amorphous metallic coatings prepared by HVOF thermal spraying[J]. Journal of Thermal Spray Technology, 2010, 19(6): 1287-1293. DOI:10.1007/s11666-010-9556-2 |
| [7] |
HE J, ICE M, LAVERNE E. Particle melting behavior during high-velocity oxygen fuel thermal spraying[J]. Journal of Thermal Spray Technology, 2001, 10(1): 83-93. DOI:10.1361/105996301770349547 |
| [8] |
ZHANG S D, ZHANG W L, WANG S G, et al. Characterization of three-dimensional porosity in an Fe-based amorphous coating and its correlation with corrosion behavior[J]. Corrosion Science, 2015, 93: 211-221. DOI:10.1016/j.corsci.2015.01.022 |
| [9] |
CHENG Z M, LIU M, DENG C M, et al. Effects of spray distance on the microstructure and property of LT-HVOF Ti coating[J]. Surface Technology, 2014, 43(4): 11-16. |
| [10] |
BANG S S, PARK Y C, LEE J W, et al. Effect of the spray distance on the properties of high velocity oxygen-fuel (HVOF) sprayed WC-12Co coatings[J]. Journal of Nanoscience & Nanotechnology, 2018, 18(3): 1931-1934. DOI:10.1166/jnn.2018.14990 |
| [11] |
王刚, 陈静, 黄仲佳, 等. 喷涂距离对热喷涂非晶合金涂层组织和腐蚀性能的影响[J]. 功能材料, 2016, 47(6): 185-189. WANG Gang, CHEN Jing, HUANG Zhongjia, et al. Effect of spraying distance on microstructure and corrosion properties of thermal sprayed amorphous alloy coatings[J]. Functional Materials, 2016, 47(6): 185-189. DOI:10.3969/j.issn.1001-9731.2016.06.034 |
| [12] |
HANSON T C, SETTLES G S. Particle temperature and velocity effects on the porosity and oxidation of an HVOF corrosion-control coating[J]. Thermal Spray Technology, 2003, 12(3): 403-415. DOI:10.1361/105996303770348276 |
| [13] |
KAMNIS S, GU S. Numerical modelling of propane combustion in a high velocity oxygen-fuel thermal spray gun[J]. Chemical Engineering and Processing: Process Intensification, 2006, 45(4): 246-253. DOI:10.1016/j.cep.2005.06.011 |
| [14] |
LI M L, SHI D, CHRISTOFIDES P D. Diamond jet hybrid HVOF thermal spray: Gas-phase and particle behavior modeling and feedback control design[J]. Industrial & Engineering Chemistry Research, 2004, 43(14): 3632-3652. DOI:10.1021/ie030559i |
| [15] |
LI M L, CHRISTOFIDES P D. Feedback control of HVOF thermal spray process accounting for powder size distribution[J]. Journal of Thermal Spray Technology, 2004, 13(1): 108-120. DOI:10.1007/s11666-004-0055-1 |
| [16] |
TABBARA H, GU S. Computational simulation of liquid-fuelled HVOF thermal spraying[J]. Surface and Coatings Technology, 2009, 204(5): 676-684. DOI:10.1016/j.surfcoat.2009.09.005 |
| [17] |
KHAN M N, SHAMIM T. Investigation of a dual-stage high velocity oxygen fuel thermal spray system[J]. Applied Energy, 2014, 130: 853-862. DOI:10.1016/j.apenergy.2014.03.075 |
| [18] |
FARMER J, CHOI J S, CHENG S, et al. Iron-based amorphous-metals: High-performance corrosion-resistant materials (HPCRM) development final report[J]. Metallurgical & Materials Transactions A, 2009, 40(6): 1289-1305. DOI:10.1007/s11661-008-9779-8 |
| [19] |
GAONA M, LIMA R S, MARPLE B R. Influence of particle temperature and velocity on the microstructure and mechanical behaviour of high velocity oxy-fuel (HVOF)-sprayed nanostructured titania coatings[J]. Journal of Materials Processing Technology, 2008, 198(1-3): 426-435. DOI:10.1016/j.jmatprotec.2007.07.024 |
 2020, Vol. 28
2020, Vol. 28


