2. 南京南汽冲压件有限公司,南京,211100
2. Nanjing Automobile Stamping Parts Co., Ltd, Nanjing 211100, China
随着高强度、经济环保的高强钢在汽车行业中的广泛应用[1],有效解决了经济环保与安全的矛盾问题,但高强钢成形性差的特性一直都是困扰企业的难点[2]。虽然很多学者对汽车冲压件的成形优化已进行了很多研究,但在寻找最优的工艺参数方面仍存在不足:有的学者[3]在有限元基础上结合人工神经网络算法,这无疑提高了模拟的预测精度,但人工神经网络的权值和阈值是随机得到的,因此,对于网络训练的结果可能存在差别;还有学者提出了将试验设计和有限元结合,以多目标优化控制的方法来寻找最佳工艺参数,进而提高成形质量[4-5],这虽具有较好的效果,但无法从工艺参数区间得到更精确的解。
根据某冲压件厂的项目要求,对新材料DP-780高强钢车身侧围板的成形质量采用有限元结合人工神经网络和遗传算法的方法进行研究。首先对新材料进行室温拉伸试验,再根据冲压成形极限图,进一步提出质量评价指标;采用正交试验仿真分析建立试验数据库,并结合BP神经网络和遗传算法,开展高强钢车身侧围板成形质量的优化研究。
1 实验为了对高强钢进行更好的仿真模拟分析,提高预测精度,需要建立实际生产所需的DP-780高强钢的材料模型[6]。本文建立的DP-780高强钢材料模型是弹塑性材料,材料的力学性能通过拉伸试验得出。试验主要测定DP-780高强钢的屈服强度、抗拉强度、断后伸长率、硬化指数、厚向异性系数等性能指标,依据国家标准GB/T 228.1-2010金属材料室温拉伸试验方法进行试验。
厚向异性系数反映材料在厚度方向上的变形难易程度,是评价板料抗减薄能力的指标;当厚向异性系数的值大于1时,说明板料在厚度方向上不容易减薄。
| $ R=\frac{\varepsilon_{b}}{\varepsilon_{t}}=\frac{\ln b / b_{0}}{\ln t_{a} / t_{0}}. $ | (1) |
式中:εb、εt为试样宽度应变和厚度应变, b0、b为试样原宽和变形后宽度, t0、ta为试样原厚和变形后厚度。
考虑到材料的各向异性,在制备试样时一般需要沿材料轧制方向0°、45°、90°的方向分别取样,再经过加权平均的方法求值,得到最终厚向异性系数:
| $ \bar{R}=\frac{r_{0}+2 r_{45}+r_{90}}{4}. $ | (2) |
式中:R为厚向异性系数, r0、r45、r90为0°、45°、90°的方向试样的厚向异性系数。
硬化指数是描述材料变形均匀性的重要参数,应变硬化指数越大,说明材料变形越均匀,降低了零件的减薄风险。硬化指数是根据试样在均匀变形阶段的两点真实应力-应变求出的[7],具体公式如下:
| $ \sigma=K \varepsilon^{n}. $ | (3) |
式中:σ、ε为试样真实应力、应变, K为试样强度系数, n为试样硬化系数。
将式(3)两边分别取对数,进行线性化处理;取2个测试点相减得出应变指标:
| $ n=\frac{\ln \sigma_{1}-\ln \sigma_{2}}{\ln \varepsilon_{1}-\ln \varepsilon_{2}}. $ | (4) |
应变硬化指数也需要对沿材料轧制方向0°、45°、90°的试样应变硬化指数进行加权求均值:
| $ n=\frac{n_{0}+2 n_{45}+n_{90}}{4}. $ | (5) |
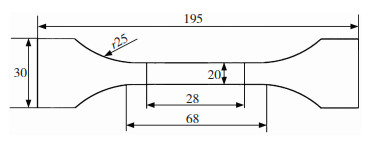
在拉伸试验中,试验所用试样的形状、尺寸、取样所在的板料位置和方向、表面粗糙度等都会对试验的结果产生影响[8]。本试验将DP-780板料制成标准试样[9],其具体尺寸如图 1所示。
|
图 1 标准拉伸试样尺寸图(mm) Fig.1 Standard tensile specimen size diagram(mm) |
试验中沿着高强板轧制方向0°、45°、90°的方向分别取3个试件,总计共9个试件。经拉伸试验机测得的材料力学性能参数如表 1所示。
| 表 1 DP-780试样材料参数 Table 1 Material parameters of DP-780 specimen |
前工程上依然采用成形极限图(FLD)来评价零件的成形质量,但这样的缺陷是不同工艺参数组合所得到成形质量无法定量的进行比较,也就无法准确地评价哪个工艺参数下的成形质量最优,所以本文根据成形极限图不同成形区域的意义,提出拉裂、起皱以及增厚-减薄的质量评价标准,这样可以定量的比较不同的成形质量结果。
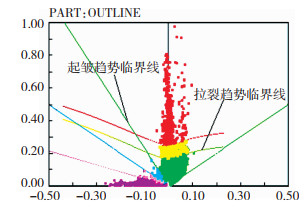
2.1 拉裂评价标准若仿真结果单元在拉裂趋势临界线以上时就具有发生拉裂的趋势,因此可用单元距离拉裂趋势临界线的远近来表示拉裂程度[10]。如图 2所示,当距离拉裂趋势临界线以上的评价单元达到一定数目时,就可准确地评价零件的拉裂质量,公式如下:
| $ F_{l}=\left(\frac{\sum _{1}^{n} \Delta f_{i}}{N}\right)^{\frac{1}{2}}. $ | (6) |
| $ \Delta f_{i}=\left\{\begin{array}{cc} \left(\varepsilon_{1}^{i}-f_{2}\left(\varepsilon_{2}^{i}\right)\right)^{2}, & \varepsilon_{1}^{i}>f_{2}\left(\varepsilon_{2}^{i}\right) \\ 0, & \varepsilon_{1}^{i} \leqslant f_{2}\left(\varepsilon_{2}^{i}\right) \end{array}\right.. $ | (7) |
|
图 2 有限元模拟成形极限图 Fig.2 Finite element simulation of forming limit diagram |
式中:N为选取的单元数, f2(x)为成形极限图上拉裂趋势曲线, ε1、ε2为主应变、次应变。
由式(6)和(7)可得,当主次应变所对应的单元处于拉裂趋势临界线以上,且距离临界线越远时,表示该单元发生拉裂的可能性越大;将这些单元进行数值统计,进而得到相应的拉裂评价标准值;显然值越小,拉裂可能性越小,成形质量越好。
2.2 起皱评价标准如图 2所示,位于起皱趋势临界线以下的仿真单元与临界线的距离也可以来表示零件发生起皱的程度[10],公式如下:
| $ W_{q}=\left(\frac{\sum _{1}^{n} \Delta w_{i}}{N}\right)^{\frac{1}{2}}. $ | (8) |
| $ \Delta w_{i}=\left\{\begin{array}{cc} \left(\varepsilon_{1}^{i}-w_{2}\left(\varepsilon_{2}^{i}\right)\right)^{2}, & \varepsilon_{1}^{i}>w_{2}\left(\varepsilon_{2}^{i}\right); \\ 0, & \varepsilon_{1}^{i} \leqslant w_{2}\left(\varepsilon_{2}^{i}\right). \end{array}\right. $ | (9) |
式中:w2(x)为成形极限图上起皱趋势曲线
由式(8)和(9)可得,当主次应变所对应的单元处于起皱趋势临界线以下,且距离临界线越远时,说明该单元发生起皱的程度越大;将这些单元进行数值统计,进而得出相应的起皱评价标准值;显然值越小,表明起皱的程度越小,成形质量越好。
2.3 减薄-增厚评价标准板料在冲压成形过程会发生塑形变形,从而引起厚度变化,若厚度变化越均匀,则说明板料的成形性越好;所以可根据成形后板料的增厚和减薄的变化率来表示零件厚度的均匀性[11],公式如下:
| $ T=\left(\frac{\sum _{1}^{n} \Delta t_{i}}{N}\right)^{\frac{1}{2}}. $ | (10) |
| $ \Delta t_{i}=\left(\frac{t_{i}-t_{p}}{t_{p}}\right). $ | (11) |
式中:ti为选取单元的厚度, tp为板料成形后的平均厚度。
由式(10)和(11)可得,板料厚度变化的均匀性取决于各个单元厚度的变化,当各单元厚度变化越接近于平均厚度时,说明成形质量越好。
3 有限元模拟设计正交试验建立数据库根据工厂要求,车身侧围板的工艺生产方案设定为拉延、翻边整形和切边冲孔。零件的成形质量贯穿整个制造工艺过程[12]。如图 3所示,在拉延工序中,选择冲压速度、压边力、摩擦系数和板料偏置尺寸作为研究的工艺参数,采用正交试验方法得到不同工艺参数下的成形质量数据库,这对工程上具有理论指导意义。

|
图 3 拉延工序仿真模型 Fig.3 Simulation model of drawing process |
冲压速度一方面影响着零件成形质量,另一方面直接影响生产效率。理论上应在不影响成形质量的基础上尽可能地提高冲压速度。但在实际板料成形过程中,冲压速度的改变反映为板料微观层面上应变速率的变化,而应变速率的变化又影响板料的塑形变形抗力[13],如式(12)所示:
| $ F_{k}=c v_{\varepsilon}^{m}. $ | (12) |
式中:Fk为板料的塑性变形抗力, Vε为应变速率, c为当Vε=1时的变形抗力, m为应变速率系数,反映冲压速度变化时板料的均匀变化能力,值越大则说明板料均匀变形能力越好。
从式(12)可得:板料的塑性变形抗力会随着板料应变速率的增加而增大,即塑性变形能力会随之减小,而不同的变形速度会使板料获得不同的成形极限[14],所以,研究冲压速度对成形性能的影响是十分必要的。
3.2 压边力在拉延过程中,若板料受到来自压边圈和凹模的压紧力十分合适,则会将工具体间产生的摩擦力增加板料的拉应力,限制板料向凹模内腔的流动速率,使材料成形充分,但过大压边力会增加进料阻力,容易使板料变薄,甚至拉裂[15]。根据式(13),需要不断地计算和调整压边力大小,使板料成形更好。
| $ F_{Q}=A q. $ | (13) |
式中:FQ为压边力(N), A为压边圈与板料的接触面积(mm2), q为单位面积上压边力(MPa)。
3.3 摩擦系数根据摩擦力公式可推导出摩擦系数:
| $ \mu=\frac{F}{F_{N}}. $ | (14) |
式中:F为摩擦力(N), FN为正压力(N)。
摩擦力直接影响板料的进料速率,影响成形质量的好坏;合理的摩擦系数使进料均匀,提高成形质量。摩擦力较大时,进料阻力相对较大,易发生应力集中现象,使零件出现划伤,甚至拉裂[16];摩擦力较小时,进料阻力相对较小,板料在压边圈和凹模之间的流动比较容易,易产生起皱等问题[17]。因此,选择合适的摩擦系数对零件的成形质量起着至关重要的作用,根据以往工程经验确定的摩擦系数如表 2所示。
| 表 2 正交试验各因子水平 Table 2 Level of each factor in orthogonal test |
合理的板料毛坯形状一方面可提高成形质量,改善成形过程中进料不均匀的问题;另一方面可减少切边时所浪费的板料,提高材料利用率,有效节约生产成本[18]。本文利用软件中的板料工程,对零件进行展开结算,得到板料的外轮廓,以轮廓为基础得出板料形状。其中,板料偏置尺寸即为在所得的板料形状轮廓线上向外偏置的尺寸。
3.5 模拟分析结果在有限元仿真模拟中,采用正交试验研究多因子对成形质量的影响是常用的方法之一[19]。由于不同工艺参数之间的匹配会得到不同的成形结果,而且不同的工艺参数水平之间的组合也会随着参数范围的变化而变化,所以设计如表 2所示正交试验来研究不同水平工艺参数对车身侧围板成形质量的影响。
根据正交试验设计共256种组合,经仿真并代入评价标准公式计算得到768个评价标准值。但工程上要求:
| $ F_{l} \leqslant 0.01, W_{a} \leqslant 0.05 $ |
因此去除其中不满足约束条件的值,得到如表 3所示的基于评价标准的部分正交试验数据库。其中A、B、C、D分别表示冲压速度、压边力、摩擦系数和板料偏置尺寸;1、2、3、4分别对应各因子水平。从得到的正交试验数据库中,依据各个标准值越小则成形质量就越好的标准,得到最佳工艺参数组合如表 4所示。
| 表 3 部分正交试验数据 Table 3 Partial orthogonal test data |
| 表 4 最佳工艺参数组合 Table 4 Optimal technological parameters combination |
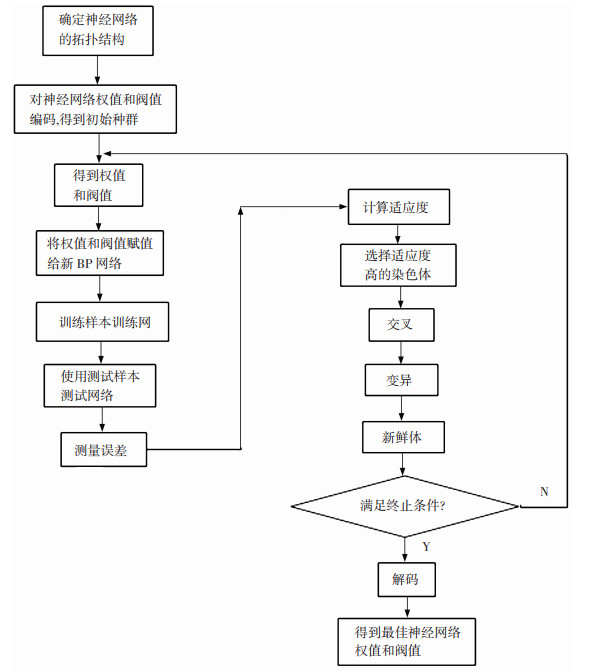
通过正交试验分析,只能得到已给的参数组合中的最佳参数,但无法更精确的获得不同工艺参数范围内的最优解[20-21],因此需要根据BP神经网络遗传优化算法,来进一步确定工艺参数范围内的最优工艺参数值,计算流程图如图 4所示。
|
图 4 神经算法流程图 Fig.4 Flow chart of neural algorithm |
BP神经网络是一类多层的前馈神经网络,结构较为简单,可进行调整的参数很多,提供的训练算法也很多,可操作性好;但存在易陷入局部极小值而得不到整体最优、训练易陷入瘫痪、收敛速度慢等缺点[22];其工作原理是在正向传播和逆向传播过程中,根据误差信号对神经元的权值和阀值不断进行优化,使误差缩小到规定的范围之内。本文采用的是BP神经网络在函数逼近上的应用,训练函数为动量梯度下降函数,即函数,在输入的样本数据与对应的输出样本数据之间建立函数关系。具体的网络设置参数和训练代码如下:
net.trainParam.epochs=200 000;
net.trainParam.goal=0.000 01;
net.trainParam.lr=0.05;
net=train(net,P,T);
Y=sim(net,P_test);
神经网络结构主要由输入层、隐含层和输出层构成。将四个工艺参数作为输入层,隐含层神经网络个数根据公式(15)确定:
| $ n_{1}=2 n_{2}+1. $ | (15) |
式中:n1为隐含层神经网络个数;n2为输入层神经元个数。
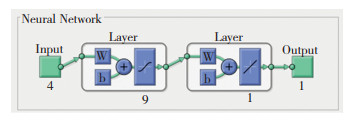
因此本文在Matlab中对应的BP神经网络结构如图 5所示,图中4代表四个工艺参数输入量;9代表隐含层神经网络个数;1代表一个输出量;W代表神经元的连接权值;b代表神经元的阀值。
|
图 5 神经网络结构图 Fig.5 Neural network structure diagram |
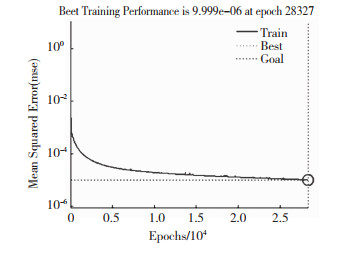
对神经网络结构开始进行训练,并不断修正权值和阈值,目的是使网络输出的误差越来越小。如图 6所示,经过28327次的迭代之后,样本误差测试达到目标值10-5。
|
图 6 神经网络训练误差图 Fig.6 Neural network training error map |
遗传算法是将问题参数编码成染色体,仿效生物界,在种群中进行选择、交叉、变异等方法交换染色体中的信息,经过不断的迭代运算,最终得到最优目标即目标染色体。对于规模较大的组合优化问题,其具有实用性高,求解效率快的优点,但随着问题规模的不断扩大,计算的步骤会变得很复杂,而且在求解过程中容易出现"早期收敛"和"遗传漂移"等现象[23]。
通过神经网络可对权值和阈值不断进行优化,但其初始值是随机得到的,通常不同的初始值得到的网络训练结果不同。所以,本文在神经网络的基础上又引入遗传算法,来进一步优化结果[24]。采用ranking适应度计算:
FitnV=ranking(ObjV)
ObjV为目标值输出,目的是使预测值更加接近于期望值。ObjV选择如下:
ObjV=zeros(M, 1);
for i=1:M
Obj(i)=Bpfun(X(i, :), P, T, hiddennum, P_test, T_test);
End
表 5为定义的遗传算法参数,则对应的代码为:
| 表 5 遗传算法运行参数 Table 5 Operation parameters of genetic algorithm |
NIND=50;
MAXGEN=50;
PRECI=10;
Px=0.95;
Pm=0.01;
GGAP=0.95
遗传算法主要是依据优胜劣汰原则来搜索运算,最后得到最优的工艺参数。对应的遗传算法的主程序为:
ObjV=Objfun(X(i, :), P, T, hiddennum, P_test);
Whlie gen < MAXGEN
Fprintf(‘%d\n’, gen)
FitnV=ranking(ObjV);
SelCh=select(‘sus’, Chrom, FitnV, GGAP)
SelCh=recombin(‘xovsp’, SelCh, Px);
SelCh=mut(SelCh, Pm);
X=bs2rv(SelCh, FieldD);
ObjVSel=Objfun(X, P, T, hiddennum, P_test, T_test);
[Chrom, ObjV]=reins(Chrom, SelCh, l, l, ObjV, ObjVSel);
X=bs2rv(Chrom, FieldD);
Gen=gen+1;
[Y, I]=min(Objv);
Trace(l:N, gen)=X(I, :);
Trace(end, gen)=Y;
End
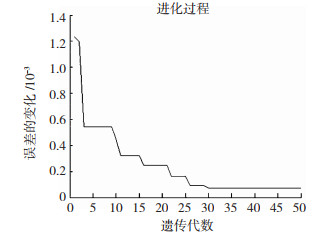
如图 7所示为50次迭代之后的目标函数误差变化曲线。
|
图 7 种群目标函数均值和最优解的变化 Fig.7 Variation of mean and optimal solution of the objective function of a population |
从图 7可知,迭代到30次时,误差就已经达到目标值0.73×10-4,此时目标函数输出最优解。最终经过数值取整得到最优的工艺参数见表 6。
| 表 6 最优工艺参数值 Table 6 Optimum process parameters |
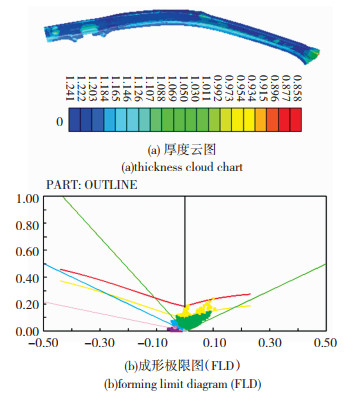
将表 6所得的最优工艺参数利用dynaform有限元软件进行仿真,得到车身侧围板最终的成形云图如图 8所示,则零件的最大减薄率和增厚率分别为28.5%和3.4%,都小于30%,满足工艺要求,成形性较好。
|
图 8 模拟分析结果 Fig.8 Simulation analysis results |
计算得到零件的拉裂、起皱和减薄-增厚的标准值分别为0.000 33、0.001 11和0.025 90;与正交试验得到结果的误差最大为0.39%,说明通过优化算法得到的结果准确。
4.4 实验结果验证在某冲压件厂的冲压模具上输入得到的最优参数值,则最终冲压成形件如图 9所示;经三坐标检测,厚度变形均匀,外观没有缺陷和毛刺,成形性好,验证了仿真分析以及优化计算的正确性。

|
图 9 最终实体图 Fig.9 Final entity diagram |
1) 依据国标对新材料DP-780板料进行室温拉伸试验,获得了材料的力学性能参数,并依据成形极限图,进一步提出冲压成形质量的评价指标;
2) 利用Dynaform仿真软件,选取工艺参数进行正交试验,得到了基于评价指标的正交试验数据库;
3) 结合BP神经网络和遗传算法来进一步求得最优解,最终获得最佳的工艺参数组合为:冲压速度4.230 m/s,压边力310 kN,摩擦系数0.13,板料偏置尺寸7.0 mm;最后经试验冲压,三坐标检测,发现成形性好,进而验证了仿真分析以及优化计算的正确性。
| [1] |
高文平.基于DYNAFORM的左后轮罩内板冲压成形过程模拟[D].长春: 吉林大学, 2014. GAO Wenping.Simulation of stamping process of inner plate of left rear wheel hood based on DYNAFORM[D]. Changchun: Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014297463.htm |
| [2] |
李贵.面向产品设计的回弹模拟与几何补偿方法研究[D].武汉: 华中科技大学, 2014. LI Gui.Research on springback simulation and geometric compensation for product design[D]. Wuhan: Huazhong University of Science and Technology, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D608932 |
| [3] |
KAZAN R, FIRAT M, TIRYAKI A E. Prediction of springback in wipe-bending process of sheet metal using neural network[J]. Materials and Design, 2009, 30(2): 418-423. DOI:10.1016/j.matdes.2008.05.033 |
| [4] |
CHEN Peng, KOC M. Simulation of variation in forming of advanced high strength steels[J]. Journal of Materials Processing Technology, 2007, 190(1/2/3): 189-198. DOI:10.1016/j.jmatprotec.2007.02.046 |
| [5] |
INGARAO G, LORENZO R D, MICARI F. Analysis of stamping performances of dual phase steels: a multi-objective approach to reduce springback and thinning failure[J]. Materials and Design, 2009, 30(10): 4421-4433. DOI:10.1016/j.matdes.2009.04.001 |
| [6] |
刘大海, 孟维金, 蒙骏鹏. DP780高强钢板材高应变率变形行为及本构模型[J]. 塑性工程学报, 2018, 25(1): 161-166. LIU Dahai, MENG Weijin, MENG Junpeng. Deformation behavior and constitutive model of DP780 high strength steel sheet with high strain rate[J]. Journal of Plastic Engineering, 2018, 25(1): 161-166. DOI:10.3969/j.issn.1007-2012.2018.01.024 |
| [7] |
金桩, 赵建平. 微载荷连续球压痕法评价金属材料的屈服强度和应变硬化指数[J]. 机械工程材料, 2018, 42(1): 72-77. JIN Zhuang, ZHAO Jianping. Evaluation of yield strength and strain hardening exponent of metal materials by micro load continuous ball indentation method[J]. Mechanical Engineering Materials, 2018, 42(1): 72-77. DOI:10.11973/jxgccl201801015 |
| [8] |
段丽霞, 刘瑜. 金属材料室温拉伸试验影响因素分析与控制要求[J]. 黑龙江科技信息, 2017(14): 102-102. DUAN Lixia, LIU Yu. Influencing factors analysis and control requirements for tensile test of metallic materials at room temperature[J]. Heilongjiang Science and Technology Information, 2017(14): 102-102. DOI:10.3969/j.issn.1673-1328.2017.14.095 |
| [9] |
高怡斐, 梁新帮, 邓星临. GB/T 228.1-2010《金属材料拉伸试验第1部分: 室温实验方法》实施指南[M].北京: 中国质检出版社, 2012. GAO Yifei, LIANG Xinbang, DENG Xinglin. GB/T 228.1-2010 Guide for the implementation of the first part tensile test of metallic materials: Laboratory method for room temperature[M]. Beijing: China Quality Inspection Publishing House, 2012. |
| [10] |
孙光永, 李光耀, 张勇, 等. 基于有限元的板料拉延成形质量评价准则及工艺参数优化研究[J]. 固体力学学报, 2009, 30(1): 70-78. SUN Guangyong, LI Guangyao, ZHANG Yong, et al. Study on quality evaluation criteria and process parameters optimization of sheet metal drawing based on finite element method[J]. Journal of Solid Mechanics, 2009, 30(1): 70-78. |
| [11] |
闫盖, 郑燕萍, 张文彦, 等. 基于正交试验的板料冲压成形工艺参数优化[J]. 热加工工艺, 2013, 42(17): 94-97. YAN Gai, ZHENG Yanping, ZHANG Wenyan, et al. Optimization of sheet metal stamping process parameters based on orthogonal test[J]. Hot Working Process, 2013, 42(17): 94-97. |
| [12] |
陆林.车身前翼子板成形质量控制与工艺参数优化[D].镇江: 江苏大学, 2016. LU Lin. Quality control and process parameters optimization of front wing panel forming[D]. Zhenjiang: Jiangsu University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10299-1016904922.htm |
| [13] |
CHENG T C, RONG S L. The influence of grain size and strain rate effects on formability of aluminium alloy sheet at high-speed forming[J]. Journal of Materials Processing Technology, 2018, 253: 134-159. DOI:10.1016/j.jmatprotec.2017.10.046 |
| [14] |
范泽.冲压速度对板料成形性能的影响研究[D].合肥: 合肥工业大学, 2015. FAN Ze. Influence of stamping speed on sheet metal formability[D]. Hefei : Hefei Polytechnic University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10359-1015669253.htm |
| [15] |
KITAYAMA S, YAMADA S. Simultaneous optimization of blank shape and variable blank holder force of front side member manufacturing by deep drawing[J]. International Journal of Advanced Manufacturing Technology, 2017, 91(1/2/3/4): 1381-1390. |
| [16] |
WANG C, MA R, ZHAO J, et al. Calculation method and experimental study of coulomb friction coefficient in sheet metal forming[J]. Journal of Manufacturing Processes, 2017, 27: 126-137. DOI:10.1016/j.jmapro.2017.02.016 |
| [17] |
DAI Longfei, XU Xuefeng, SUN Qianjiang, et al. Influence of friction coefficient on internal high pressure forming for thin-walled T-shaped tube[J]. Forging & Stamping Technology, 2018, 43(7): 159-164. |
| [18] |
HABIBI M, ADDA-BEDIA M, BONN D. Effect of the material properties on the crumpling of a thin sheet[J]. Soft Matter, 2017, 13(22): 4029-4034. DOI:10.1039/C6SM02817A |
| [19] |
王列亮.多因素对铝合金板冲压成形质量影响的研究[D].南京: 南京林业大学, 2015. WANG Lieliang. Study on the influence of multiple factors on the quality of aluminum alloy sheet forming[D]. Nanjing: Nanjing Forestry University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10298-1015809203.htm |
| [20] |
郭水军, 聂威, 杨旭静, 等. 基于冲压成形困难区域的拉延筋阻力稳健设计[J]. 现代制造工程, 2015(11): 106-112. GUO Shuijun, NIE Wei, YANG Xujing, et al. Robust design of drawbead resistance based on difficult stamping forming region[J]. Modern Manufacturing Engineering, 2015(11): 106-112. DOI:10.3969/j.issn.1671-3133.2015.11.023 |
| [21] |
DONG L, XING T, ZHOU S, et al. Optimization of forming process parameters for automobile engine cover based on orthogonal experiment[J]. Forging & Stamping Technology, 2016, 41(11): 62-64. DOI:10.13330/j.issn.1000-3940.2016.11.012 |
| [22] |
Y U BS, WANG S, YANG T, et al. BP neural netwok constitutive model based on optimization with genetic algorithm for SMA[J]. Acta Metallurgica Sinica, 2017, 53(2): 248-256. |
| [23] |
MADRASWALA H S. Modified genetic algorithm solution to unit commitment problem[C]// International Conference on Nascent Technologies in Engineering. Vashi, Navi Mumbai, India: IEEE, 2017: 1-6.
|
| [24] |
郁磊. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2015. YU Lei. 30 cases analysis of MATLAB intelligent algorithm[M]. Beijing: Beihang University Press, 2015. |
 2020, Vol. 28
2020, Vol. 28


