复合材料在先进民机上的运用越来越多,越来越普遍;尤其是机翼、机身壁板类组件[1]。壁板根据长桁的形式不同,通常有“工”形长桁壁板、帽形长桁壁板、“Z”形长桁壁板和“T”形长桁壁板[2]。对类似长桁壁板的承载研究较多,如:刘均等[3]对复合材料壁板中长桁的胶接应力进行了分析,提出节点力法计算胶接应力,在线弹性下得到胶接应力与长桁刚度突变的关系;刘衰财等[4]对复合材料壁板与钛合金接头连接的强度进行了实验和分析,得到混杂结构的载荷传递路径以及危险螺栓位置;孙启星等[5-6]对复合材料壁板筋条的斜削区失效进行分析,采用强度与能量准则预测脱层扩展与结构的失效载荷;吴承思等[6]对复合材料“T”形长桁壁板的破坏模式进行了研究,对长桁/蒙皮刚度比提出了设计建议; 还有多位学者对复合材料长桁的终止端进行了承载研究[7-11],对终止端的几何参数提出了优化建议。然而,目前多数研究都是针对局部结构的承载性能进行的,但对所采用的有限元方法的准确性与合理性鲜有分析。本文运用工程、有限元、试验3种方法对试验件承压性能进行研究,探讨工程方法和有限元方法的特点,并验证了有限元方法的合理性。
1 试验 1.1 试验件试验件的形式和参数来自某型号民用飞机的中央翼复合材料上壁板长桁。在选用长桁形式时,考虑到各种截面的长桁承载特性、国内复合材料结构成型工艺水平及装配的复杂程度等,最终选用“T”形长桁。以靠近前梁的第一根长桁的尺寸为参数,设计了复合材料“T”形长桁试验件。
试验件长桁材料为高温固化中模碳纤维增强M21E增韧环氧树脂复合材料。材料牌号为M21E/34%/UD194/IMA-12K/600 HLU,预浸料单层板的厚度为0.186 8 mm,材料参数见表 1。
| 表 1 M21E预浸料单层板的力学性能 Table 1 Mechanical properties of M21E prepreg monolayer |
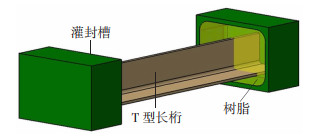
“T”形长桁试验件长度均为270 mm,两侧端头各35 mm,树脂封闭,长桁实际承载长度为200 mm。试验件承受压缩载荷,对两端面的平行度及试验件的垂直度要求较高。两端面之间的平行度要求为0.02,试验件与端面之间的垂直度要求为0.04。试验件结构形式如图 1所示。
|
图 1 “T”形长桁试验件示意图 Fig.1 Test part of "T" stringer |
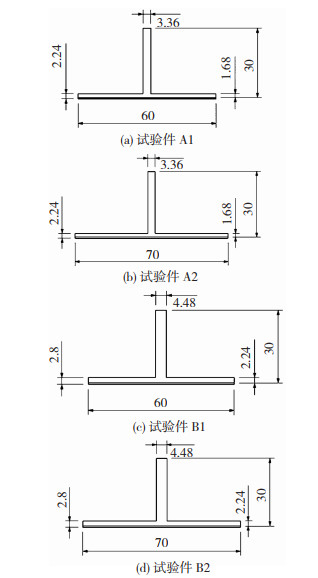
“T”形长桁由“L”形背靠背铺层和底部“一”形铺层共同组合而成,通过共胶接连接成一体。长桁缘条厚度等于“L”形铺层厚度加上“一”形铺层厚度;长桁腹板的厚度为“L”形铺层厚度乘以2。“L”形铺层有2种,“一”形铺层有1种,长桁缘条的宽度有2种,可以组成如表 2中4种试验件,即A1、A2、B1和B2。每种类型试验件3件,共计12件。“T”形长桁-蒙皮剖面形状及尺寸如图 2所示。
| 表 2 长桁铺层顺序 Table 2 Long truss layer sequence |
|
图 2 “T”形长桁-蒙皮剖面(单位:mm) Fig.2 Cross section of "T" stringer |
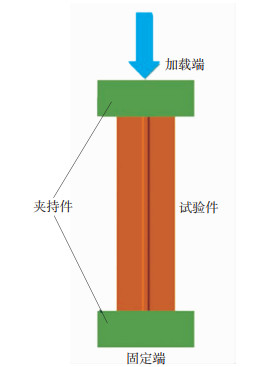
试验在INSTRON 8804试验机上进行,试验件垂直放置在试验机加载平台上直接进行端部压缩加载,加载方式如图 3示,载荷合力作用点(试验机加载中心)与长桁截面压心一致,加载速率为0.5 mm/min。图 4为试验件在试验机上的装夹状态图。
|
图 3 加载方式示意图 Fig.3 Loading mode |

|
图 4 试验件装夹 Fig.4 Test piece clamping |
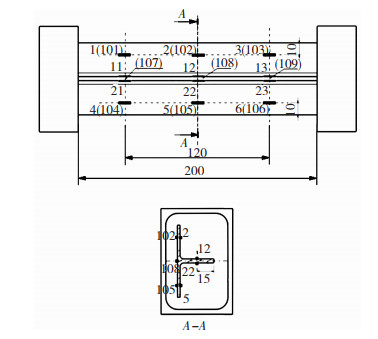
在试验件长桁缘条、长桁腹板上粘贴应变片, 以记录压缩过程中的应变随载荷的变化,应变片粘贴位置及编号如图 5所示。
|
图 5 贴片位置及标号示意图 Fig.5 Position and label of strain gauge |
“T”形长桁压缩试验中,12件试验件的试验现象较为相似,故选取A1试验件的第2件试验件(A1-2)为例进行详细分析。在载荷加载至25 kN时开始出现轻微响声,随着载荷逐级增加,轻微响声持续发生;当加载至约80 kN时,试验件产生巨大声响,试验件破坏,腹板断裂且缘条出现撕裂。试验件的破坏模式如图 6所示,该试验件的最终破坏位置为距端面约1/4处,破坏部位有大量的纤维断裂,部分纤维成碎片。

|
图 6 A1-2试验件最终破坏模式 Fig.6 Failure mode of A1-2 |
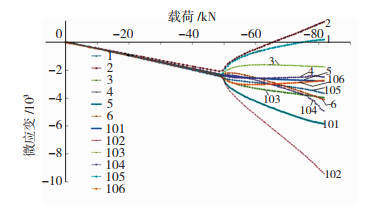
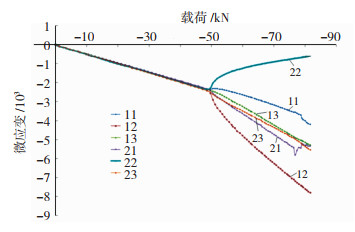
图 7、图 8分别为试验件A1-2长桁的缘条载荷-应变曲线和腹板载荷-应变曲线,可以看到:在加载初始阶段,载荷小于48 kN时,长桁缘条和腹板上载荷-应变曲线呈线性一致的变化趋势(压缩应变为负值),此阶段试验件在加载方向上呈均匀的压缩变形;当载荷大于48 kN后,长桁缘条和腹板上的载荷-应变同时开始呈现出一致的非线性,曲线出现明显的“分叉”现象,即产生了屈曲失稳,对应的屈曲载荷为48 kN。
|
图 7 A1-2长桁缘条的载荷-应变曲线 Fig.7 Load-strain curves of A1-2 flange |
|
图 8 A1-2长桁腹板的载荷-应变曲线 Fig.8 Load-strain curves of A1-2 web |
从应变片得到的应变数值也可以计算出单元产生局部屈曲时的载荷。根据A1试验件的铺层和单层板的力学性能,用有限元计算出长桁缘条的弹性模量为74.1 GPa。对A1-2试验件,局部屈曲发生在102号应变片处,屈曲微应变为2 212。可按下式计算局部屈曲载荷。
| $ F = SE\varepsilon . $ | (1) |
式中:S是长桁缘条的截面积;E是长桁缘条的弹性模量;ε是单元局部屈曲时应变片的应变值。经计算,A1-2试验件长桁缘条处局部屈曲载荷为367.1 N/mm。
其余11件试验件的载荷应变趋势与A1-2试验件呈现出较高的一致性,试验现象及破坏形式较为相似,对应的试验结果如表 3所示。
| 表 3 试验测试值、工程算法计算和有限元分析结果 Table 3 Test values, engineering algorithms, and finite element analysis results |
12件试验件中有11件的破坏发生在距离端面约1/4~1/3处,只有1件发生在中间位置,见图 9。这是因为试验加载难以达到理想状态,载荷无法完全集中在试验件中心线上,试验件会产生附加弯矩。

|
图 9 试验件从中间破坏示意图 Fig.9 Damage of test piece from the middle |
采用经典工程算法计算"T"形长桁的局部屈曲载荷和压损载荷[12-15]。
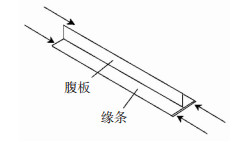
2.1 局部屈曲载荷计算方法长桁局部屈曲载荷的分析模型见图 10。计算步骤如下。对于开口薄壁剖面长桁的缘条,当作一长边自由,另一长边简支的长板处理,可按下式计算缘条的轴压局部屈曲载荷。
| $ {N_{{\rm{xcr}}}} = \frac{{{\rm{ }}12{D_{66}}}}{{{b_{\rm{t}}}^2}} + \frac{{{\pi ^2}{D_{11}}}}{{{L^2}}}. $ | (2) |
|
图 10 长桁中缘条和腹板 Fig.10 Flange and web of stringer |
式中:Nxcr为单位宽度上的轴压屈曲载荷;bt为缘条的宽度;L为长桁的长度;D11,D66为层压板的纵向弯曲刚度,扭转刚度。
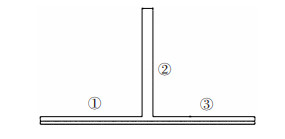
长桁包含2个底部缘条、1个腹板共3个单元(见图 11),计算得到到各个单元的屈曲载荷,将最小值作为长桁的局部屈曲载荷。
|
图 11 分析所对应的3个单元 Fig.11 Three analytical units |
以A1试验件为例,根据其铺层(见表 2)和单层板性能(见表 1),通过有限元计算出各个单元的弯扭刚度Dij,见表 4。
| 表 4 各单元弯扭刚度 Table 4 Flexural and torsional stiffness of each element |
A1、A2、B1、B2试验件按式(2)工程算法计算的长桁局部屈曲载荷如表 3所示。
2.2 压损载荷计算方法长桁压损载荷计算方法如下。
| ${{\sigma _{{\rm{cc}}}} = m \times {{\left( {\frac{{b\bar E}}{{t{E_{{\rm{xc}}}}}}\sqrt {\frac{{{\sigma _{{\rm{cu}}}}}}{{\sqrt {{E_{{\rm{xc}}}}{E_{{\rm{yc}}}}} }}} } \right)}^{\rm{e}}}\frac{{{\sigma _{{\rm{cu}}}}\bar E}}{{{E_{{\rm{xc}}}}}}, } $ | (3) |
| $ {{\sigma _{{\rm{cu}}}} = {\varepsilon _{{\rm{cr}}}}{E_{{\rm{xc}}}}, } $ | (4) |
| $ {\bar E = \frac{{12{D_{11}}}}{{{t^3}}}\left( {1 - {\mu _{{\rm{xy}}}}{\mu _{{\rm{yx}}}}} \right), } $ | (5) |
| $ {{\mu _{{\rm{yx}}}} = {\mu _{{\rm{xy}}}}\frac{{{E_{{\rm{yc}}}}}}{{{E_{{\rm{xc}}}}}}.} $ |
式中:σcc, σcu为压损许用值;b为单元宽度;t为单元厚度; εcr为层压板纤维方向的压缩许用值;Exc为层压板x方向的面内刚度;Eyc为层压板y方向的面内刚度;μxy、μyx为—层压板面内等效泊松比;对于单元①、单元②和单元③:m=0.575,e=-0.797。
取各组成单元(见图 11)的σcc和σcu中的最低值,求其加权平均值得到压损许用值。
| $ {\sigma _{{\rm{cc}}}} = \frac{{\sum\limits_{i = 1}^N {{\rm{min}}({\sigma _{{\rm{cc}}}}^i, {\sigma _{{\rm{cu}}}}^i){b_i}{t_i}} }}{{\sum\limits_{i = 1}^N {{b_i}{t_i}} }}. $ | (6) |
压损载荷Fcc计算公式为
| $ {F_{{\rm{cc}}}} = {\sigma _{{\rm{cc}}}}\sum\limits_{i = 1}^N {{b_i}{t_i}} . $ | (7) |
以A1试验件为例,该“T”形长桁的材料力学参数如表 5所示。
| 表 5 材料力学参数 Table 5 Mechanics parameters of materials |
A1、A2、B1、B2试验件按式(3)至式(7)工程算法计算的长桁压损载荷如表 3所示。
3 “T”形长桁受压承载有限元分析基于ABAQUS有限元分析平台,建立有限元模型计算“T”形长桁的屈曲载荷和压损载荷。
本文中,长桁缘条和长桁腹板采用S4R壳单元进行离散,单元数目满足计算精度要求。为了提高计算效率,模型中忽略层与层之间的粘接和R区填充的捻子条,因此,有限元模型未计及分层失效以及捻子条对长桁受压承载能力的影响[16]。材料的损伤判据采用ABAQUS内嵌的二维Hashin准则[17]和基于能量的损伤演化方法,具体参数由试验获得。
根据试验夹具及加载情况对模型进行简化。试验件两侧端头外的参考点位于长桁剖面压心连线上,两个参考点分别与长桁两侧端头(长度为35 mm)的6个自由度耦合约束。一侧的参考点上施加轴向压缩单位载荷,同时约束该参考点除轴向平动方向的另外5个自由度;另一侧的参考点进行固支约束。屈曲分析有限元模型如图 12所示,对其进行特征值屈曲分析。

|
图 12 “T”形长桁屈曲分析有限元模型 Fig.12 Buckling finite element model of "T" stringer |
“T”形长桁的压损分析有限元建模如图 13所示,建模方法与线性屈曲分析模型相同,只需在一端施加2 mm的轴向强迫压缩位移。同时,引入线性屈曲分析得到的位移变形的1%作为初始几何缺陷,进行非线性分析。

|
图 13 “T”形长桁压损有限元分析模型 Fig.13 Pressure loss finite element model of "T" stringer |
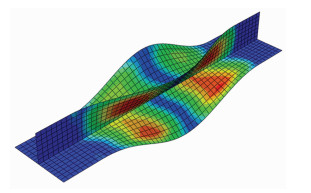
以A1试验件为例,进行有限元计算。“T”形长桁一阶屈曲振型图如图 14所示,在长桁腹板和底部缘条上均出现1个轴向屈曲波,长桁的屈曲载荷约为46.1 kN。图 14中出现的屈曲位置与试验结果屈曲位置相近。
|
图 14 “T”形长桁压缩一阶屈曲振型 Fig.14 Compression of first-order buckling modes of "T" stringer |
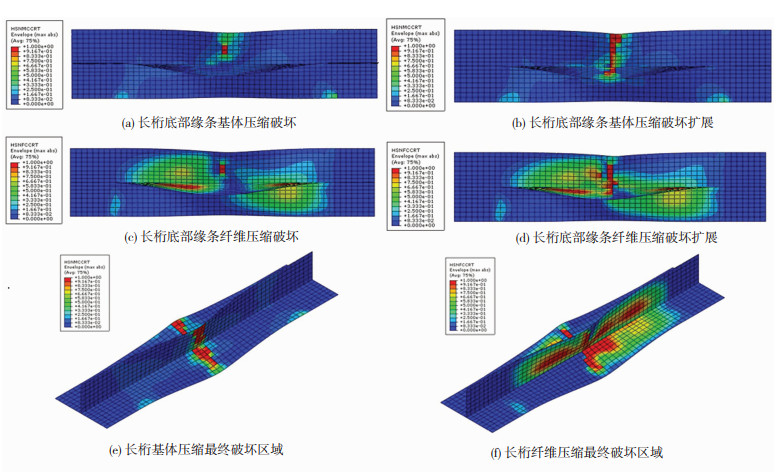
试验件在轴向压缩作用力下的破坏过程如图 15所示。首先在长桁底部缘条发生基体的压缩破坏(图 15(a));随着压缩载荷的增加,基体压缩破坏逐渐向缘条中间扩展(图 15(b)),接着长桁底部缘条的纤维发生压缩破坏(图 15(c))和破坏扩展(图 15(d));最终扩展至长桁腹板(图 15(e));而后,该处和长桁腹板发生纤维压缩破坏(图 15(f))。从整个破坏过程来看,基体压缩破坏、纤维压缩破坏模式均出现,纤维压缩破坏区域最大。
|
图 15 “T”形长桁受压破坏模拟 Fig.15 Compression failure simulation of "T" stringer |
通过图 15(f)与图 9对比可知,破坏发生在“T”形长桁的中间位置,说明仿真结果与试验最终破坏形貌相似。
长桁不同部位破坏形式见表 6。
| 表 6 长桁不同部位破坏形式 Table 6 Damage forms of different parts of stringer |
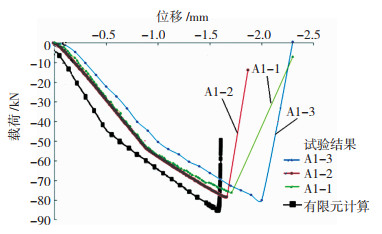
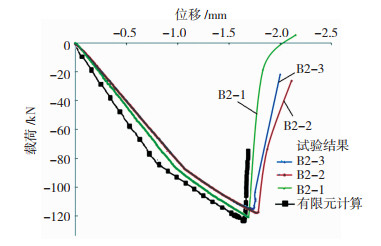
图 16和图 17是分别采用有限元计算和试验测试得到的两试验件的长桁载荷-位移曲线。A1件,B2件有限元计算所得压损载荷为86.7、121.2 kN。压损载荷计算结果高于试验值,经分析是因为有限元分析中未区别建立捻子条模型,而在真实试验过程中,长桁在屈曲之后,捻子条和长桁及蒙皮出现了脱粘,降低了整个长桁的轴向刚度。另外,计算所得的长桁压缩位移比试验值要小。计算存在误差,且试验件在受压过程中有些许弯曲,灌封槽里面的长桁端面在初始阶段可能未紧贴槽底,导致试验测得的位移偏大。有限元计算结果见表 3。
|
图 16 A1试验件载荷-位移曲线 Fig.16 Load-displacement curves of A1 |
|
图 17 B2试验件载荷-位移曲线 Fig.17 Load-displacement curves of B2 |
试验测试值、工程算法计算和有限元分析得到的结果均列于表 3。由表 3可知,“T”形长桁局部屈曲载荷工程计算值比试验值小8%~20%;压损载荷工程计算值比试验值小35%~50%。
“T”形长桁屈曲载荷有限元计算值在试验值附近,误差在10%以内;压损载荷有限元计算值均高于试验值,误差小于10%。原因可能是有限元模型中未区别建立捻子条模型,而在真实试验过程中,长桁在屈曲后,捻子条和长桁出现了脱粘,降低了整个长桁的轴向刚度。
对“T”形长桁,增加缘条宽度和腹板厚度均可提高承载能力,其中增加腹板厚度更能显著提高承载能力,但缘条的宽度厚度比过大, 屈曲载荷反而会减小。
5 结论1)“T”形长桁工程计算得到的局部屈曲载荷、压损载荷均小于试验值,计算结果分散性高,因此工程算法偏保守。
2) 有限元方法预测的屈曲载荷、压损载荷与试验值相比较,误差在10%以内,两者吻合较好。简化的有限元模型计算效率高,模型简单,计算精度满足工程要求,能够为设计人员提供设计依据。
3) 合理优化“T”形长桁缘条的宽度厚度比,有利提高长桁的结构效率。
| [1] |
唐见茂. 航空航天复合材料发展现状及前景[J]. 航天器环境工程, 2013, 30(4): 342-359. TANG Jianmao. Current status and trends of advanced composites in aerospace[J]. Spacecraft Environment Engineering, 2013, 30(4): 342-359. |
| [2] |
杨乃宾, 章怡宁. 复合材料飞机结构设计[M]. 北京: 航空工业出版社, 2002: 205-210. YANG Naibin, ZHANG Yining. Structure design of composite aircraft[M]. Beijing: Aviation Industry Press, 2002: 205-210. |
| [3] |
刘均, 黄宝宗. 复合材料壁板中长桁的胶接应力分析[J]. 辽宁工程技术大学学报, 2007(5): 35-37. LIU Jun, HUANG Baozong. Analysis of adhesive stresses of stiffeners in stiffened composite panels[J]. Journal of Liaoning Technical University, 2007(5): 35-37. |
| [4] |
刘衰财, 刘伟. 复合材料壁板与钛合金接头连接强度试验与分析[J]. 机械设计与制造工程, 2017(1): 55-58. LIU Shuaicai, LIU Wei. Analysis and experiment on connection strength between the composite panel and titanium joint[J]. Machine Design and Manufacturing Engineering, 2017(1): 55-58. |
| [5] |
孙启星, 陈普会. 复合材料壁板筋条斜削区失效分析[J]. 南京航空航天大学学报, 2008(4): 94-98. SUN Qixing, CHEN Puhui. Failure analysis of composite panels in stiffener runout region[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008(4): 94-98. |
| [6] |
REINOSO J, BLÁZQUEZ A, TÁVARA L. Damage tolerance of composite runout panels under tensile loading[J]. Composites Part B: Engineering, 2016(96): 85-91. |
| [7] |
吴承思, 李冬梅, 李庆飞. T型复合材料长桁承载能力设计研究[J]. 纤维复合材料, 2013, 30(2): 51-53. WU Chengsi, LI Dongmei, LI Qingfei. Research on load capacity design of composite T-joint[J]. Fiber Composites, 2013, 30(2): 51-53. |
| [8] |
中国航空研究院. 复合材料结构稳定性分析指南[M]. 北京: 航空工业出版社出版, 2002: 217-218. Chinese Aeronautics Research Institute. A guide for structural stability analysis of composite materials[M]. Beijing: Aviation Industry Press, 2002: 217-218. |
| [9] |
陈亚军. 复合材料加筋壁板长桁终止端失效分析[J]. 科学技术与工程, 2014(31): 102-111. CHEN Yajun. Numerical study on failure at stiffener runout of stiffened composite panel[J]. Science Technology and Engineering, 2014(31): 102-111. |
| [10] |
刘婷, 周凯华. 复合材料加筋板长桁终止端设计与分析[J]. 南京航空航天大学学报, 2013(3): 77-81. LIU Ting, ZHOU Kaihua. Design and analysis of laminated stiffened composite panels with stringer terminations[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013(3): 77-81. |
| [11] |
杜芳静, 王亮. 复合材料长桁终止端设计[J]. 沈阳航空航天大学学报, 2016(2): 24-28. DU Fangjing, WANG Liang. Composite stringer runout design[J]. Journal of Shenyang Aerospace University, 2016(2): 24-28. |
| [12] |
牛春匀. 实用飞机结构应力分析及尺寸设计[M]. 北京: 航空工业出版社, 2009: 641-655. NIU Chunyun. Airframe stress analysis and sizing[M]. Beijing: Aviation Industry Press, 2009: 641-655. |
| [13] |
邱志平, 王晓军. 飞机结构强度分析和设计基础[M]. 北京: 航空航天大学出版社, 2012: 136-139. QIU Zhiping, WANG Xiaojun. Structural strength analysis and design basis of aircraft[M]. Beijing: Beihang University Press, 2012: 136-139. |
| [14] |
杨静宁, 马连生. 复合材料力学[M]. 北京: 北京国防工业出版社, 2014: 179-181. YANG Jingning, MA Liansheng. Mechanics of composite materials[M]. Beijing: National Defense Industry Press, 2014: 179-181. |
| [15] |
赵美英. 复合材料结构力学与结构设计[M]. 西安: 西北工业大学出版社, 2007: 144-146. ZHAO Meiying. Structural mechanics and structural design of composite materials[M]. Xi'an: Northwestern Polytechnical University Press, 2007: 144-146. |
| [16] |
关玉璞, 陈伟. 航空航天结构有限元法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014: 162-174. GUAN Yupu, CHEN Wei. Finite element method for aeronautics and astronautics[M]. Harbin: Harbin Institute of Technology Press, 2014: 162-174. |
| [17] |
HASHIN Z. Fatigue failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics, 1980, 47(2): 329-334. DOI:10.1115/1.3153664 |
 2020, Vol. 28
2020, Vol. 28


