在钢结构领域中,Q235b工字钢梁具有加工方便、成本较低等优点,在房屋建筑和桥梁工程中得到了广泛应用,并且在结构设计中属于优先选用的构件形式[1]。但是在制造和使用过程中,钢梁构件由于受长期复杂荷载的作用,以及外界环境等因素的影响,其承载力、刚度、稳定性较设计时都有所下降,会产生微观损伤等,在一定情况下可能会引起结构的失效,造成严重的安全问题,这就使得对钢结构构件的检测成为必要[2]。因此,进行建筑钢结构中工字钢梁构件无损检测技术的研究至关重要。目前该检测技术已经被应用到了轨道、管道、压力容器,飞机起落架等铁磁性构件安全检测当中[3]。相比于其它方法,金属磁记忆法操作简单,灵敏度高,不用对构件进行检测前的处理。这种检测方法可对铁磁构件应力集中区域及存在隐性损伤的部位进行早期发现,并采取有效的预防措施,防止铁磁构件的突然破坏,有早期预警的作用[4]。金属磁记忆检测技术有望在建筑钢结构等工程中的早期健康检测得到广泛应用[5]。
金属磁记忆检测技术是一种新兴的磁无损检测方法,其基本原理是,在外加磁场和应力的作用下,铁磁材料内部将发生磁畴壁移动和磁矩转动,在构件表面出现磁场强度的改变,损伤区域产生自有漏磁场,并且存在“记忆”现象,宏观上表现在磁记忆信号的法向与切向两个分量上为:切向分量具有最大值,而法向分量改变符号且具有零值点[6-7]。围绕金属磁记忆技术的力-磁耦合效应国内外学者进行了许多数值模拟的研究,IVANOV[8]等曾利用ANSYS有限元软件进行了在球形压力载荷作用下铁磁性管道产生残余应力和大内凹形变后管件表面的漏磁通分布的模拟。任吉林等[9-10]对18CrNi4A钢的力-磁耦合过程进行了模拟,得到在不同载荷下的磁记忆信号变化规律。姚凯等[11-12]通过数值模拟的方式分析了45号钢弹塑性变形与磁记忆信号之间的关系,并且模拟研究了缺陷尺寸、提离值等对磁信号的影响。苏三庆等[13-15]进行了钢丝绳和建筑钢板件拉伸的力磁模拟。之前学者的模拟及试验研究,为金属磁记忆力-磁耦合关系的研究及提供了一定的参考和帮助,但之前的数值模拟大多是建筑领域之外小构件的研究,并且以单向均匀受力为主,且将金属磁记忆检测技术应用到建筑钢结构检测领域正处于理论研究阶段。
因此,选用建筑钢结构中常用的Q235b工字钢梁来进行受弯时复杂应力作用下磁记忆检测的力磁耦合效应的模拟,以实现从构件到结构的仿真研究。本文通过ANSYS有限元软件,对四点受弯作用下钢梁进行了模拟与试验的验证,并对框架中常见的均布荷载作用下两端固结钢梁进行了力磁耦合效应的模拟。得到均布荷载作用下钢梁的漏磁场信号和其梯度的分布情况,并提出用应力集中截面处平均磁信号和平均磁信号梯度值表征危险截面处应力变化情况和应力集中程度。为今后金属磁记忆检测技术在建筑钢结构领域的应用提供了基础。
1 力-磁耦合模拟 1.1 力磁耦合本构模型力磁耦合本构模型定义磁导率为应力的函数,将力场与磁场结合起来。应力的磁效应来源于应力的磁导率效应的理论可以很好的解释金属磁记忆现象,机械应力以及材料组织本身的不均匀性导致材料磁导率分布的不均匀性,进而在外界地球磁场的作用下引起漏磁场,漏磁场的大小取决于磁导率的不均匀程度。
铁磁性构件在外荷载和地磁场共同作用下,其内部应力能的变化会导致材料宏观磁特性(如磁导率、矫顽力等)的改变。结合现有的应力与磁导率模型应用条件以及多次试算,本文模拟采用的力磁本构为俄罗斯动力诊断公司采用经验数据提出的微磁场下铁磁构件的力磁耦合模型,如式(1)所示。
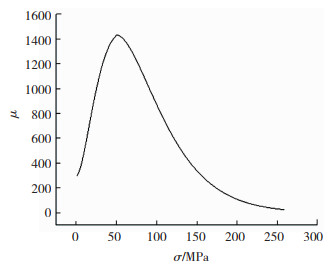
| $ \mu = {\mu _T}\left( {1 + \frac{{bH}}{{{\mu _T}}}} \right)[{a_0} + {a_1}|\sigma {|^m}\cdot{e^{n|\sigma |}}] $ | (1) |
式中:μ为施加应力后的磁导率;μT为初始磁导率;H=39.8 A/m为地磁场的大小,b=2.5为与材料本身性质相关的常数;a0,a1,m,n为与荷载方向和应力值有关的系数。当σ<50 MPa时,a0=0.768 04;a1=0.000 916;m=1.904 12;n=-0.033 53;当σ≥50 MPa时,a0=-0.004 47;a1=0.041 08;m=1.554 99;n=-0.031 48。
根据式(1)可得磁导率-应力本构关系,如图 1所示。
|
图 1 磁导率-应力耦合模型 Fig.1 ermeability-stress coupling model |
本文采用ANSYS软件,采用间接耦合的方式对受弯工字型钢梁进行了力-磁耦合的模拟。模拟构件为长度1.5米,14号热轧工字钢梁,本次模拟先在静力场中进行构件力学计算,求得钢梁的应力值,再通过应力与磁导率的关系模型求得每个单元的磁导率,然后在磁场中将磁导率赋予构件的每个单元,最终求得钢梁的磁场变化。
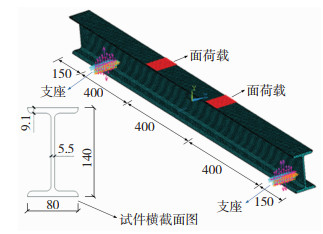
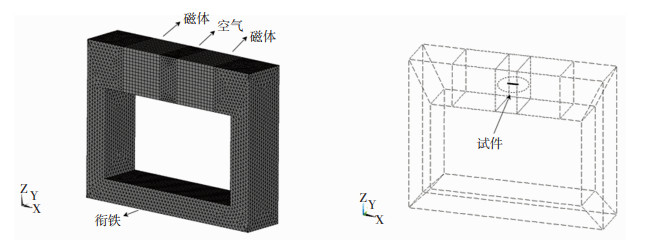
静力场中模型尺寸、加载与约束方式如图 2所示。磁场模拟的三维模型如图 3所示,模型分为试件、衔铁和空气3部分,设大地磁场强度约为40 A/m,衔铁两端设置永磁体用来模拟地磁场,其相对磁导率设置为1.08,空气和衔铁的相对磁导率分别设置为1和186 000,用以形成闭合磁力线,让试件所处的空间磁场形成一个均匀的大地磁场环境[16]。磁场采用三维磁标量法进行模拟,因此使用solid96单元,该单元为三维8节点六面体单元,节点自由度为磁标势MAG[17]。而静力场分析中为保证与静磁场中的单元契合,采用三维8节点六面体实体单元soild185,并且划分的单元大小与数量保持一致,保证力场与磁场在耦合时单元一一对应。
|
图 2 试件尺寸及加载方式图(单位: mm) Fig.2 Specimen size and loading mode |
|
图 3 磁场三维模型示意图 Fig.3 Three-dimensional model of magnetic field |
首先进行力场计算,加载时为和试验保持一致,将集中力换算为面荷载施加,由计算可得该梁屈服强度为110 kN,故设置加载等级为20、40、60、80、100、110 kN,每级荷载下静力计算完成后提取单元等效应力值,计算得到每个单元对应的磁导率。然后在ANSYS磁场中,通过数组和改写命令将得到的磁导率每个赋予单元,在磁场模拟中磁通量平行边界自动满足,只需要试件两端施加垂直边界条件。在试件中除了输入不同的磁导率之外还需要施加矫顽力,以此来模拟剩磁场作用。计算对应荷载下的磁信号特征值,静磁计算完成后,分别提取各等级荷载与地磁场组合作用下试件表面的漏磁场法向磁信号分量以分析应力作用下磁场分布情况。
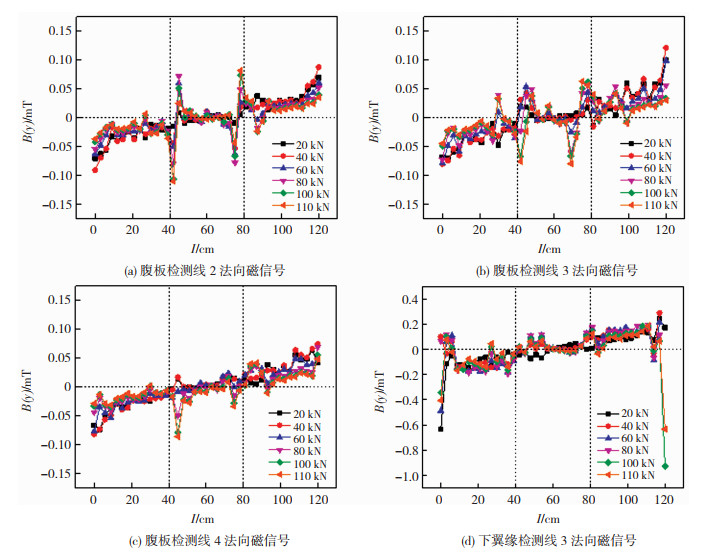
1.3 有限元模拟结果分析在磁场计算完成后提取翼缘和腹板指定路径上的磁感应强度法向分量B(y)如图 4所示。结果表明,磁信号法向分量整体曲线过零点,而且由于钢梁的加载方式为对称加载,磁信号曲线亦有一定的对称性。腹板在加载点40 cm和80 cm区域磁感应强度B出现过零点和波峰波谷现象,而翼缘在支座处则出现这一现象。翼缘加载点处的一定区域内出现轻微的波峰波谷现象,这是由于加载点和支座处出现了应力突变造成的。腹板中间纯弯段应力最小,磁信号法向分量在零点附近波动。
|
图 4 有限元模拟的磁信号法向分量曲线 Fig.4 The curve of the normal component of magnetic signal of the modeling:(a) web detection line 2 normal magnetic signal; (b) web detection line 4 normal magnetic signal; (c) web detection line 4 normal magnetic signal; (d) lower flange detection line 3 normal magnetic signal |
腹板中间三分之一区域内随着荷载的增加磁信号数值基本不变,在零点附近波动,近似呈现一条过零点的直线;两个加载点处磁信号峰值随着荷载的增加不断增大,到达屈服时有所减小;中间段以外的两边区域磁信号数值随着荷载的增加而减小;其整体磁信号曲线除加载点和支座处以外,其余可近似看作一条斜直线,其斜率随着荷载的增加而减小。翼缘磁信号曲线除支座处以外,在加载的初始阶段其斜率随荷载的增加而增大,接近屈服时斜率随着荷载的增加而减小;左边支座处磁信号峰值随荷载的增加而增大,接近屈服时减小;右边支座处磁信号峰值随荷载的增加而减小,接近屈服时增大。
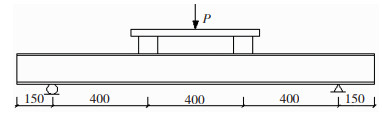
2 集中力作用下受弯工字型钢梁静载试验 2.1 试验过程本次试验为工字钢梁4点受弯试验,材料选用常用Q235B,14号热轧工字钢。其材料化学成分,基本力学参数与初始磁特性参数如表 1,表 2所示。试验中为测得每阶段的磁信号变化情况,采取分级加载,保载在线测量。试件尺寸、加载制度和模拟一致,检测线的布置如图 5所示,腹板等间距选取5条检测线,分别编号为1,2,3,4,5。翼缘选取3条检测线,分别编号为1,2,3。试验中采用在线点测方法,检测点间距为5 cm,检测时保持探头垂直紧贴于试件表面,读取表面漏磁场磁感应强度法向分量B(y)值。试件加载方式如图 6,在受力段的两个三分点翼缘板上方,居中各设置一个方钢垫块,作为转换构件。试验在YAW5000型液压伺服压剪试验机上进行,磁记忆信号检测设备选用高精度WT10B型数字高斯计,最大量程为200 mT,分辨率为0.01 mT。
| 表 1 Q235B钢材化学成分(质量百分数/%) Table 1 Q235b steel chemical composition(wt.%) |
| 表 2 Q235B钢材的力学和磁学参数 Table 2 Mechanics and magnetic parameters of Q235b steel |

|
图 5 腹板和翼缘板测线布置图 Fig.5 The packing of the abdominal plate and the flange plate |
|
图 6 试件加载方式示意图(单位:mm) Fig.6 Specimen loading mode |
试验得到不同检测线上磁信号法向分量B(y)的变化曲线如图 7所示。腹板在加载点处出现明显的波谷,检测线2、3在加载点附近出现过零点现象,并且左侧三分之一段磁信号小于零,右侧三分之一段磁信号大于零。翼缘磁信号在支座附近变化幅度较大,中间段呈现斜直线,变化幅度较小,磁信号整体小于零。

|
图 7 试验中钢梁磁信号法向分量曲线 Fig.7 The curve of the normal component of magnetic signalin the test:(a) magnetic signal curve of web detection line 2; (b) magnetic signal curve of web detection line 3;(c) magnetic signal curve of web detection line 4; (d) magnetic signal curve of lower flange detection line 3 |
腹板磁信号曲线在加载点处随着荷载的增加,数值不断减小;在右边三分之一区域随着荷载的增加磁信号数值不断减小;腹板检测线2、3磁信号曲线在中间段随着荷载的增大数值基本不变,检测线4磁信号曲线在中间段随着荷载的增加,初始阶段不断增大,接近屈服时减小。翼缘磁信号曲线在中间段近似斜直线,随着荷载的增加其数值不断增大,屈服时减小;右边支座处磁信号曲线随着荷载的增加而减小,屈服时有所增大。
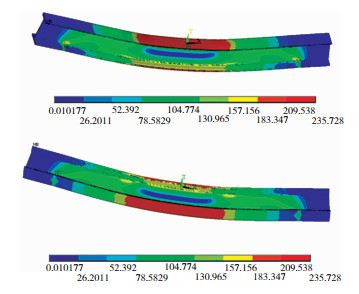
3 对有限元结果的验证分析试件加载局部进入塑性时Von Mises应力云图如图 8所示,上下翼缘纯弯段应力较大,腹板中间应力最小,翼缘加载点处出现最大应力,腹板在支座处出现最大应力。这是由于钢梁受力过程中翼缘主要承受弯矩,而中间纯弯段弯矩最大,腹板主要承受剪力,中间段剪力为零。因此模型计算符合钢梁理论受力情况,说明静力场计算正确,模型建立有效。
|
图 8 钢梁局部进入塑性时应力云图 Fig.8 The stress cloud map of the steel beam in the local plastic |
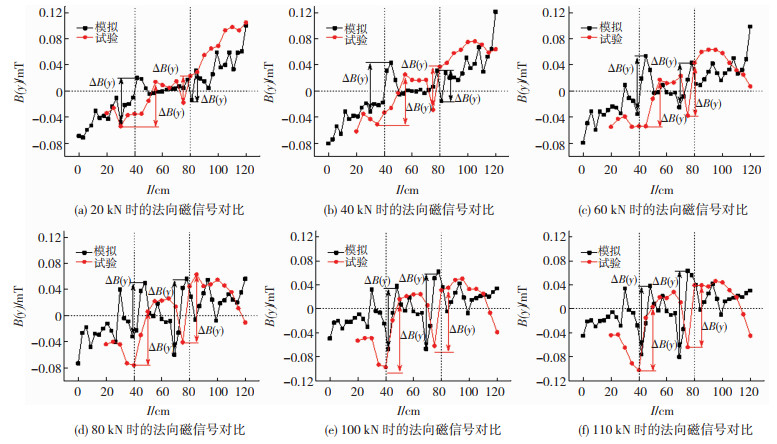
将模拟和试验中得到的磁信号曲线进行对比发现,试验中腹板检测线在加载点区域出现过零点和明显的波谷,翼缘在支座处磁信号变化较大,这和模拟可以很好的对应,但腹板加载处波峰不明显,翼缘磁信号全为负值。这是因为试验环境中加载仪器等都为铁磁材料,且试件与加载设备直接接触,加载设备体积远大于试件,因此对试件磁信号影响较大,还有试验时测点布置不够密集等引起的[13]。为了进一步说明模拟的可行性,选取钢梁腹板中间检测线3模拟与试验采集的磁信号分量数值进行分析。由于4点受弯钢梁在加载点处受力最大,出现应力突变,处于危险区域,磁信号在这一区域出现过零点和波峰波谷现象,峰峰值可作为特征量以实现利用磁性号对构件的应力集中区进行预测。故提取峰峰值ΔB(y)进行模拟和试验的对比。各加载等级下的试验与模拟磁信号法向分量对比如图 9所示,峰峰值ΔB(y)对比如表 3所示。由图 9和表 3可知,试验和模拟的磁信号曲线大体一致,钢梁控制截面即加载点区域磁信号峰峰值相差较小。
|
图 9 腹板检测线3试验和模拟的磁信号法向分量对比 Fig.9 The contrast of the normal component of magnetic signal of experiment and simulation on abdominal plate detection line 3:(a) comparison of normal magnetic signals at 20 kN; (b) comparison of normal magnetic signals at 40 kN; (c) comparison of normal magnetic signals at 60 kN; (d) comparison of normal magnetic signals at 80 kN; (e) comparison of normal magnetic signals at 100 kN; (f) comparison of normal magnetic signals at 110 kN |
| 表 3 腹板检测线3试验和模拟磁信号曲线峰峰值对比 Table 3 The contrast of the curve of magnetic signal value of peak of experiment and simulation on abdominal plate detection line 3 |
总体上,模拟的计算结果和试验数据的变化趋势相符合,证实了模拟结果的可靠性,本文有限元模型可用于建筑中钢梁的磁记忆有限元分析。磁记忆检测技术在结构中的应用在于通过建立应力与磁信号的关系,检测磁信号的变化来反映试件表面或内部的应力变化,从而对构件的损伤进行检测与预警。本文中虽然模拟和试验的数值不完全相同,但是误差在可控范围内,如表 3所示。变化规律和范围仍然相似,可以定性的说明钢梁损伤情况,对应力集中程度进行监测。
4 均布荷载作用下两端固结工字钢梁的模拟金属磁记忆检测技术在建筑钢结构领域的应用研究属于初步探索阶段,为了便于研究,采用从小构件到大构件,再到整体结构的思路,本次选用钢框架结构中的工字钢梁进行模拟,在实际工程中框架梁多承受均布荷载,产生固端弯矩。因此,基于上文中集中荷载作用下4点受弯钢梁模拟确实可行的基础上,对均布荷载作用下两端固结钢梁进行模拟分析。
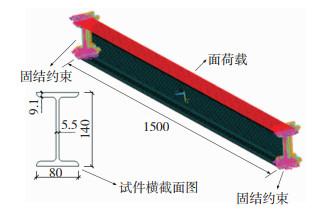
4.1 建模及加载构件模型仍采用长度为1.5米,14号热轧工字钢梁,模拟方法及思路与集中荷载作用下受弯钢梁相同,静力场计算时有限元模型及加载方式如图 10所示,磁场中计算时三维模型不变,如图 3所示。计算得到屈服荷载为110 N/mm,所以加载等级设置为20、40、60、80、100、110 N/mm,将线荷载换算为面荷载施加到整个梁上翼缘。力场和磁场计算完成后,分别提取各等级荷载作用下试件表面的漏磁场法向磁信号分量。
|
图 10 试件尺寸及有限元加载示意图(单位:mm) Fig.10 Specimen size and Finite element loading mode |
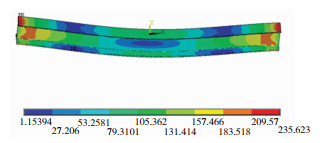
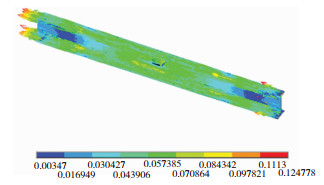
在每级荷载下分别进行静力场和磁场的计算,钢梁110 N/mm时Von Mises应力云图如图 11所示,最大应力区域在钢梁两端,翼缘五分之一处和腹板中间应力最小,符合理论受力情况。110 N/mm时钢梁表面磁感应强度矢量云图如图 12所示。
|
图 11 110 N/mm时钢梁应力云图 Fig.11 Steel beam stress cloud map in 110 N/mm |
|
图 12 110 N/mm时钢梁表面磁感应强度云图 Fig.12 The magnetic induction intensity cloud map of the steel beam surface in 110 N/mm |
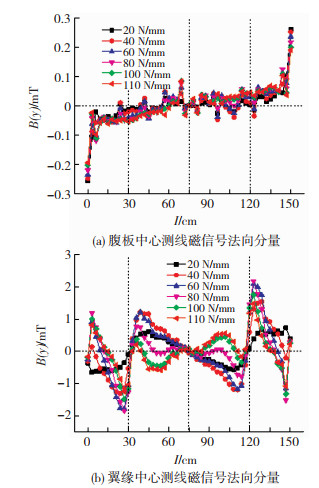
由于本次模拟考虑等效应力作用下磁场的变化,均布荷载作用时上下翼缘应力分布和大小相同,所以上下翼缘磁信号变化相同。每级加载完成后提取腹板和翼缘表面漏磁场磁感应强度法向分量如图 13所示。在应力和地磁场共同作用下,试件内部产生了很高的应力能,在试件内部的位错聚集处磁畴壁必将发生不可逆的重新取向,使原本均匀的磁力线出现畸变,从而在试件表面产生不等的自有漏磁场,随着应力的增大,试件内部逐渐达到磁饱和状态,磁信号的分布趋于稳定[18-19]。
|
图 13 钢梁磁信号法向分量曲线 Fig.13 The curve of the normal component of magnetic signal of the steel beam:(a) normal component of magnetic signal of web center line; (b) normal component of magnetic signal of the flange center line |
腹板磁信号整体曲线在试件中心处过零点,左侧在零点以下波动,右侧在零点以上波动,呈现中心对称。试件两端出现磁信号突变现象,在应力最大的6 cm和144 cm局部出现轻微的波峰波谷,两端应力集中处磁信号数值随应力增大而减小,而中间区域随应力增大而增大。
翼缘磁信号曲线在梁端和五分之一处出现过零点现象,并有较大的幅值,这是由于这两处出现应力突变,微观磁畴改变导致磁信号由负值变为正值,并且随着应力磁信号数值呈现先逐渐增大,到接近屈服时减小的趋势。当荷载大于20 N/mm时梁端磁信号开始出现正负变化,越接近屈服幅值越大。翼缘中间应力变化较均匀,磁信号刚开始加载呈现过零点的斜线,左边为正右边为负,随着接近屈服出现磁信号正负反转。
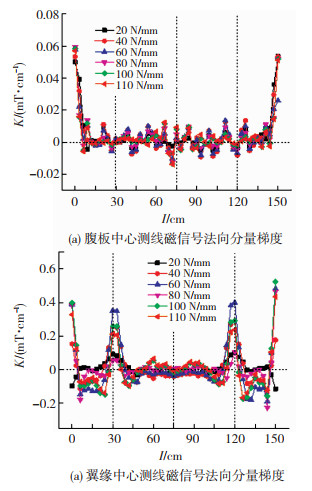
4.3 力与磁信号特征量分析磁信号梯度值K可以反应磁信号变化的快慢程度,K=dB(y)/dL,是表征磁场与应力关系的重要参量。作出钢梁表面漏磁场磁信号法向分量梯度曲线如图 14所示,只有在梁端和翼缘应力最小处出现磁信号梯度值突变,其他都在零点附近波动,这与应力变化有很好的对应关系。提取110 N/mm时的磁信号梯度值和应力进一步对比分析,如图 15所示,其他荷载等级下变化规律与此相似。当相邻应力增量增大时对应的磁信号梯度变化幅度随之增大。钢梁腹板的应力在两端到中间的数值由大到小呈现线性均匀变化,所对应的磁信号梯度值则在零点波动较小,而应力变化趋势改变时,磁信号也随之突变。翼缘磁信号梯度变化曲线与应力变化曲线相似,只是在应力最小处发生了翻转。因此磁信号梯度值能反应钢梁应力最大和最小处的应力变化幅值和趋势。
|
图 14 钢梁磁信号法向分量梯度曲线 Fig.14 The curve of the gradient of the normal component of magnetic signal of the steel beam:(a) normal component gradient of magnetic signal of web center line; (b) normal component gradient of the magnetic signal of the flange center line |

|
图 15 110 N/mm时钢梁磁信号法向分量梯度值和应力曲线 Fig.15 The curve of the gradient of the normal component of magnetic signal and stress of the steel beam in 110 N/mm:(a) agnetic signal gradient and stress curve of web intermediate line; (b) magnetic signal gradient and stress curve of the middle measuring line of the flange |
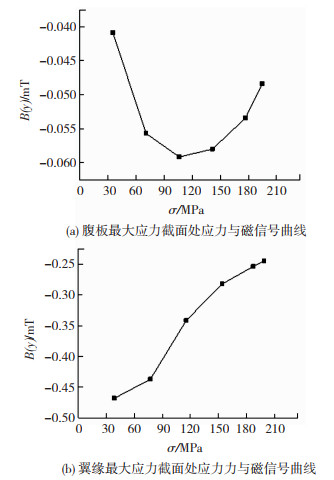
由于梁在受力过程中应力变化通常发生在某一截面而不是一点,且框架梁在受力过程中易在梁端出现塑性铰而失效。因此分别计算腹板和翼缘检测线在梁端应力集中处5条检测线的磁信号与磁信号梯度的算术平均值,作为特征量来表征危险截面处应力变化情况。建立应力与应力最大截面平均磁信号和平均梯度的关系曲线如图 16、17所示,腹板最大应力截面在6 cm处,翼缘在梁端0 cm处。
|
图 16 应力最大截面处应力与平均磁信号关系曲线 Fig.16 The curve of the relationship stress with average magnetic signal in maximum stress section:(a) stress and magnetic signal curve at maximum stress section of web; (b) stress force and magnetic signal curve at the maximum stress cross section of the flange |
|
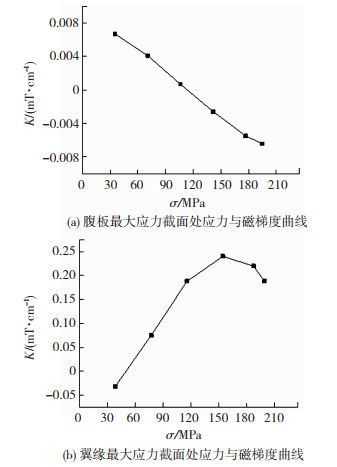
图 17 应力最大截面处应力与平均磁信号梯度关系曲线 Fig.17 The curve of the relationship stress with average the gradient of magnetic signal in maximum stress section:(a) stress and magnetic gradient curve at maximum stress section of web; (b) stress and magnetic gradient curve at the maximum stress section of the flange |
腹板在最大应力截面处磁信号均值B(y)avg在初始阶段随应力的增大数值增大明显,这是由于构件由最初的磁畴无规则变化到受力作用后重新统一取向,漏磁场增大所致。中间段增大幅度较小,接近屈服时随着力的增大呈现减小趋势,而磁信号梯度均值Kavg线性变化,为一条过零点的斜直线。接近屈服时,由有效场理论可知,应力作用下磁场已至饱和状态,试件内部磁畴重新取向已基本完成,磁畴壁的移动已达最大,最终向磁滞状态逼近,所以随着应力的增大磁记忆信号强度逐渐减小[20]。
翼缘在应力最大截面处磁信号均值B(y)avg的数值整体随力的增加而增大,在初始阶段接近屈服时随力的变化增长较缓。相应的磁信号梯度均值Kavg在初始阶段线性变化,接近屈服时随应力的增大而减小。可以得出均布荷载作用下钢梁应力集中截面处的磁信号和梯度的均值可以用来表征该截面的应力变化程度。
4.4 模拟结果分析模拟的磁信号能精确的表现应力集中出现的位置,由磁信号作出的梯度曲线变化情况和应力曲线变化也具有很好的对应性,磁信号曲线和梯度曲线都能反映钢梁的应力变化。由文章中集中力作用下钢梁的模拟和试验对比情况可知,试验中受到加载设备和外界条件的影响,模拟数值和试验有一定的误差,但变化趋势一致,仍然可以定性判断应力变化。且模拟情况对理论的发展和试验都具有指导意义。以后研究将进行该梁试验的验证,结合模拟结果精确得到磁记忆信号与应力之间的量化关系。
5 分析与讨论Jiles等[21-22]认为,力-磁效应的物理本质是应力和磁场作用的等效性,即应力和磁场分别对铁磁材料中磁畴壁的作用是等效的,应力引起的磁化与外磁场无关。通过沿着可逆的无滞后磁化曲线的系统能量A,可确定应力作用下的附加磁场Hσ[23]。
在应力和地磁场的共同作用下,铁磁试件所处的有效场He为式(2)[24]。
| $ {H_e} = H + \alpha M + {H_\sigma } $ | (2) |
式中:H为外加磁场;αM材料的磁化强度决定;Hσ来自磁畴间的磁弹性效应,为应力作用的等效磁场。
根据文献[23],铁磁性构件在外加应力和地磁场作用下的有效场为系统能量对磁化强度的导数,有效场He可表示为式(3)。
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {H_e} = \frac{1}{\mu }{{\left( {\frac{{\partial A}}{{\partial M}}} \right)}_T}}\\ {H + \alpha M + \frac{3}{2}\frac{\sigma }{{{\mu _0}}}{{\left( {\frac{{{\rm{d}}\lambda }}{{{\rm{d}}M}}} \right)}_T}} \end{array} $ | (3) |
式(2)与式(3)相比较,即可得到等效应力场的表达式如式(4)所示。
| $ {H_\sigma } = \frac{3}{2}\frac{\sigma }{{{\mu _0}}}{\left( {\frac{{{\rm{d}}\lambda }}{{{\rm{d}}M}}} \right)_T} $ | (4) |
由上式可以得出,对于某一特定材料,应力σ与等效应力场Hσ成正比,应力的磁效应与外磁场无关,即在零磁环境下应力同样可以使试件磁化,即可以检测到磁信号以表征应力。这是因为应力作用下铁磁材料的微观磁畴结构发生了改变,但是宏观上不显示磁性,虽然应力作用的自发磁化效应与外磁场无关,但能够在外磁场作用下得以表现和验证[25]。
将磁致伸缩系数λ确定为磁化强度M和应力σ的函数,采用泰勒级数展开的方式确定λ如式(5)所示[26]。
| $ \begin{array}{l} \lambda = [{\gamma _1}\left( 0 \right) + \gamma {\prime _1}\left( 0 \right)\sigma ]{M^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{\gamma _2}\left( 0 \right) + \gamma {\prime _2}\left( 0 \right)\sigma ]{M^4} \end{array} $ | (5) |
式中:由试验数据可得[27],γ1(0)=7×10-18m2/A2,γ′1(0)=1×10-25m2/A2,γ2(0)=-3.3×10-30m2/A2,γ′2(0)=2.1×10-38m2/A2。
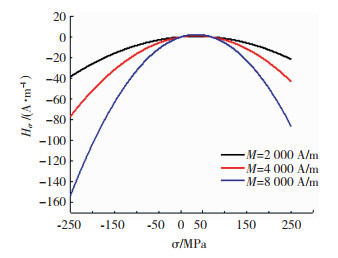
将式(4)带入式(5)可得式(6)。由式(6)可得地磁场下应力场Hσ随应力σ的变化,如图 18所示。
| $ \begin{array}{l} {H_\sigma }{\rm{ = }}\frac{{3\sigma }}{{{\mu _0}}}\left\{ {\left[ {{\gamma _1}\left( 0 \right) + \gamma {\prime _1}\left( 0 \right)\sigma } \right]} \right.M + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {{\gamma _2}\left( 0 \right) + \gamma {\prime _2}\left( 0 \right)\sigma } \right]\left. {{M^3}} \right\} \end{array} $ | (6) |
|
图 18 应力场Hσ随应力σ的变化曲线 Fig.18 The change curve of the stress field Hσ with the stress σ |
本文中钢梁属于复杂的应力状态,故采用Von Mises应力等效为简单应力进行分析。以上理论正好说明了文章中磁信号变化与等效应力相对应的情况。表明磁信号的变化趋势可以确定应力变化情况,以此为依据可以判定构件损伤情况。并且可以得到,应力磁效应是应力对材料微观结构和磁畴状态的影响产生的。
6 结论1) 本文应用有限元模拟的方法对集中荷载作用下四点受弯工字钢梁进行了力磁效应的模拟,发现试件表面漏磁场的磁信号分布趋势、幅值分布范围和变化情况与试验结果相吻合,即磁信号法向分量整体曲线过零点,并随着应力的增大而增加,磁信号曲线呈现一定的对称性。腹板在加载点区域磁信号出现过零点和明显的波谷,且幅值变化对应的曲线横坐标宽度与加载区域一致。翼缘在支座处磁信号发生突变。证明了该数值模拟方法可用于建筑结构中钢梁受弯的磁记忆有限元分析;
2) 通过对均布荷载作用下两端固结钢梁的有限元模拟,得到了钢梁表面漏磁场的磁信号法向分量及其梯度的变化曲线。发现均布荷载作用下漏磁场磁信号法向分量和磁信号法向分量梯度曲线都在应力最大和最小处发生突变,磁信号梯度曲线能反应出钢梁应力最大和最小的区域、应力变化幅度及趋势;
3) 分别定义了钢梁应力集中截面腹板和翼缘的平均磁信号B(y)avg和平均磁信号梯度Kavg,并给出了其与应力的变化关系,可以用来表征该截面的应力变化情况。为金属磁记忆检测技术定量评估提供参考。
| [1] |
陈绍蕃, 顾强. 钢结构.上册, 钢结构基础[M]. 第三版. 北京: 中国建筑工业出版社, 2014.
|
| [2] |
姚楠.在役桥梁钢结构损伤检测与安全评估相关方法的研究[D].北京: 清华大学, 2009.
|
| [3] |
邢海燕, 徐敏强, 李健伟. 磁记忆检测技术及工程应用[M]. 北京: 中国石化出版社, 2011.
|
| [4] |
徐滨士, 董丽红. 再制造质量控制中的金属磁记忆检测技术[M]. 北京: 国防工业出版社, 2015.
|
| [5] |
苏三庆, 王威. 建筑钢结构磁记忆无损检测[M]. 北京: 科学出版社, 2019.
|
| [6] |
BULTED D P, LANGMAN R A. Origins of the magnetomechanical effect[J]. Joural of Magetism and Magnetic Materials, 2000, 251(2): 229-243. DOI:10.1016/S0304-853(02)00588-7 |
| [7] |
DOUBOV A A. A study of metal peoperties using the method of magnetic memory[J]. Metal Science and Heat Treatment, 1997, 39(9): 401-405. DOI:10.1007/BF02469065 |
| [8] |
IVANOV P A. Magnetic flux leakage modeling for mechanical damage in transmission pipelines[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3020-3023. DOI:10.1109/20.717706 |
| [9] |
任吉林, 舒铭航, 伍家驹, 等. 18CrNi4A钢力-磁效应的ANSYS模拟[J]. 材料工程, 2001, 11: 40-44. REN Jiling, SHU Minhang, WU Jiaju, et al. Simulation of Stress-magnetization Effect on 18CrNi4A Steel by ANSYS[J]. Materials Engineering, 2001, 11: 40-44. |
| [10] |
REN Jilin, SHU Minghang, SONG Kai, et al. Simulation of Stress-magnetization Effect on 18CrNi4A Steel by ANSYS[C]//. 17th World Conference on Nondestructive Testing, 25-28 Oct 2008, Shanghai: 2008.
|
| [11] |
姚凯, 王正道, 邓博, 等. 金属磁记忆技术的数值研究[J]. 工程力学, 2011, 28(9): 218-222. YAO Kai, WANG Zhengdao, DENG Bo, et al. Numerical study on metal magnetic memory technioue[J]. Engineering Mechanics, 2011, 28(9): 218-222. |
| [12] |
YAO Kai, SHEN Kai, WANG Zhengdao, et al. Three-dimensional finite element analysis of residual magnetic field for ferromagnets under early damage[J]. Journal of Magnetism and Magnetic Materials, 2014, 354: 112-118. DOI:10.1016/j.jmmm.2013.10.047 |
| [13] |
苏三庆, 高波, 王威, 等. 建筑钢板件力磁效应的ANSYS有限元模拟研究[J]. 西安建筑科技大学学报(自然科学版), 2016, 48(6): 771-775. SU Sanqing, GAO Bo, WANG Wei, et al. Research on ANSYS finite element simulation of stress-magnetization effect on tensile steel plate[J]. Journal of Xi 'an University of Architecture and Technology (Natural Science edition), 2016, 48(6): 771-775. DOI:10.15986/J.1006-7930.2016.06.001 |
| [14] |
SU Sanqing, MA Xiaoping, WANG Wei, et al. Stress-dependent magnetic charge model for micro-defects of steel wire based on the magnetic memory method[J]. Research in Nondestructive Evaluation, 2019, 1: 1-24. DOI:10.1080/09349847.2019.1617914 |
| [15] |
苏三庆, 马小平, 王威, 等. 有关大地磁场对金属磁记忆信号影响的数值模拟[J]. 西安建筑科技大学学报(自然科学版), 2019, 51(4): 463-470. DOI:10.15986/j.1006-7930.2019.04.001 |
| [16] |
姚凯.基于金属磁记忆法的铁磁材料早期损伤检测与评价的实验研究[D].北京交通大学, 2012.
|
| [17] |
谢龙汉, 李杰鸿. ANSYS电磁场分析[M]. 北京: 电子工业出版社, 2015.
|
| [18] |
任吉林, 林俊明, 池永滨, 等. 金属磁记忆检测技术[M]. 北京: 中国电力出版社, 2000.
|
| [19] |
YAO Kai, WANG Zhengdao, DENG Bo, et al. Experimental research on metal magnetic memory method[J]. Experimental Mechanics, 2012, 52: 305-314. DOI:10.1007/s11340-011-9490-3 |
| [20] |
JILES D C. Introduction to Magnetism and Magnetic Materials[M]. 2nd edn. London: Chapman and Hall Press, 1998.
|
| [21] |
JILES D C, DEVINE M K. Recent developments in modeling of the stress derivative of magnetization in ferromagnetic materials[J]. Journal of Applied Physics, 1994, 76(10): 7015-7017. DOI:10.1063/1.358072 |
| [22] |
SABLIK M J, JILES D C, et al. Coupled Magnetoelastic Theory of Magnetic and Magnetostrictive Hysteresis[J]. IEEE Transactions on Magnetics, 1993, 29(3): 2113-2123. DOI:10.1109/20.221036 |
| [23] |
SABLIK M J, BURKHARDT G L, JILES D C, et al. A model for the effect of stress on the low-frequency harmonic content of the magnetic induction in ferromagnetic materials[J]. Journal of Applied Physics, 1988, 63(8): 3930-3932. DOI:10.1063/1.340609 |
| [24] |
SABLIK M J, KWU H, JILES D C, et al. Model for the effect of tensile and compressive stress on ferromagnetic hysteresis[J]. Journal of Applied Physics, 1987, 61(8): 3799-3801. DOI:10.1063/1.338650 |
| [25] |
李新蕾.金属磁记忆检测机理的试验研究与有限元仿真[D].南昌航空大学, 2010. LI Xin-lei. Basic Research on the Mechanism of Metal Magnetic Memory Testing and Finite Element Simulation [D].Nanchang: Nanchang Hangkong University, 2010. |
| [26] |
JILES D C. Theory of the magnetomechanical effect[J]. Journal of Applied Physics, 1995, 28: 1537-1546. |
| [27] |
CULLITY B D, GRAHAM C D. Introduction to Magnetic Materials[M]. 2nd edn. Wiley: Hoboken, 2011.
|
 2020, Vol. 28
2020, Vol. 28


