球头销是汽车主要零部件之一,广泛应用在汽车转向系统中,工作时受力复杂以及性能需求提高,对球头销成形的研究具有较大的社会价值。球头销的规格较多,目前主要加工方法有机加工、冷锻、楔横轧。机加工属于去除材料加工,具有材料利用率低、生产效率较低、机械性能不足等缺点,已无法满足日益增长的社会需求。楔横轧工艺主要是通过一副楔形模具轧制成形,是连续的局部成形,使工件产生径向压缩和轴向延伸[1]。多楔的合理分配,可以提高成形效率而广泛应用在轴类零件上[2]。而对于异形件与非对称件,会出现轴向受载不平衡、缩颈等不良缺陷[3]。冷锻工艺是利用模具将工件锻造成为所需要的形状。合理分配工序数是保证冷锻产品的质量与经济性的关键因素。多工位冷锻工艺具有节能减材料、高效率、高精度等优点,备受国内外企业与学者的关注。相对于楔横轧工艺,冷锻工艺工件材料流动更为简单、模具更为简易、通用性更好[4]。
对于本文六角球头销,其外形较小且为异形,采用冷锻成形更为合适。而冷镦锻作为冷锻的重要工序之一,其研究对冷锻成形具有很好的经济价值与推广意义。近年来,国内外很多学者利用有限元技术对冷镦锻成形进行工艺优化,大大增加了研发进程以及减少了研发成本。J. Landre[5]等学者利用韧性断裂准则结合有限元技术对冷镦锻成形过程中断裂进行预测,得到了断裂临界损伤值。Toshihiko Moria[6]等利用有限元方法研究了冷锻成形因素与载荷、应变、模具之间的关系。梁建平[7]等利用有限元软件模拟冷镦挤的成形过程,得到了成形过程中的流动速度场与温度场,获得了可行的成形工艺。张臻[8]等利用Deform-3D对阶梯轴成形过程进行数值仿真,得到了成形过程中的流动规律以及载荷变化规律,从而证明设计的合理性,并通过实验验证。为了能更加直观简便的对冷锻成形进行工艺优化,很多学者通过建立优化模型对工艺参数进行评估,得到直观的数据来评价成形工艺。Hu[9]等学者建立数学模型结合试验对冷锻成形工艺参数进行了优化,王可胜[10]等利用有限元软件对手机壳的冷挤压工艺进行研究,结合正交试验对坯料厚度、摩擦系数、变形速度等工艺参数进行了优化。潘小迎[11]等学者基于DEFORM软件,采用遗传算法对法兰滑套预成形的工艺参数进行优化,并得到了最优参数组合。吴先洋[12]等学者基于响应面法建立了设计变量与目标的响应面模型,通过响应面法与有限元模拟结合的方式对齿轮成形工艺进行了工艺优化。为冷镦锻成形的工艺优化、缺陷预测、有限元分析等提供了参考。
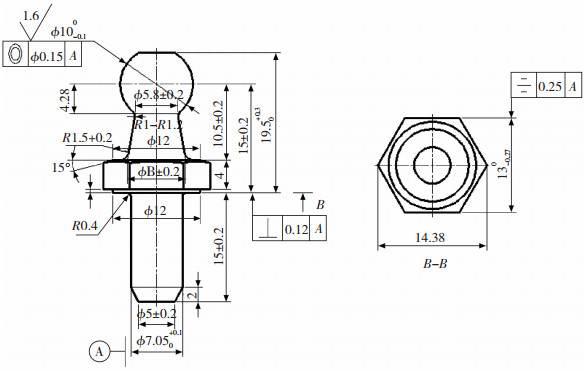
1 冷镦锻成形分析本文六角球头销的零件图,如图 1所示,材料为SWRCH35K,其力学性能见表 1。根据零件特性,零件成形主要分为六角头成形与球头成形。利用金属成形体积不变原理,得到六角头一次成形的高径比为5.47,远大于冷镦锻失稳极限2.5[13]。根据零件结构特点,考虑到六角头成形困难,先预成形再镦锻,对于预成形的形状成为成形质量的关键。
|
图 1 六角球头销零件图(单位:mm) Fig.1 Detail drawing of hex ball pin |
| 表 1 材料力学性能 Table 1 Mechanical properties of material |
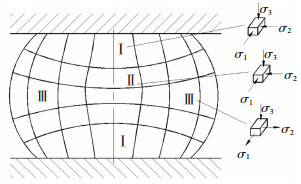
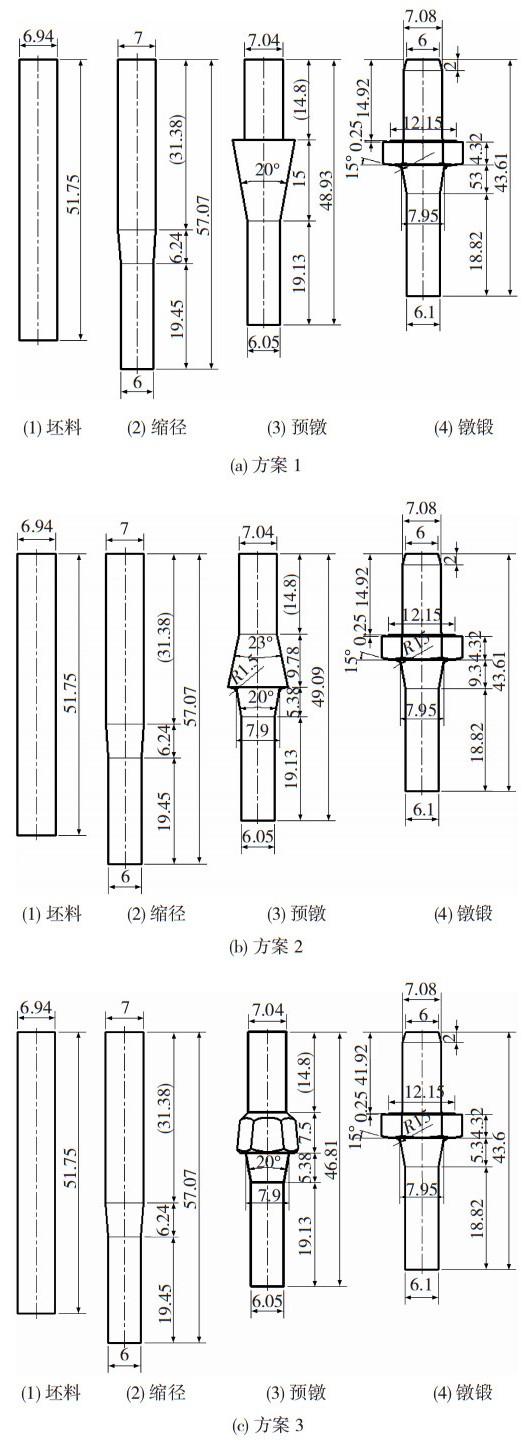
对镦锻成形进行分析,如图 2所示。Ⅰ区为难变形区,处于三向压应力状态,毛坯与模具相接触处的阻力要大于非接触处阻力,由金属塑性变形理论最小阻力定律可知,金属先沿最小阻力处成形。毛坯先向凹模的端面流动,随着冲头的下移与模具之间的相互作用,毛坯径向流动成锥形。Ⅱ区为大变形区,金属轴向变形的阻力要大于径向变形的阻力,轴向压力下产生压缩变形,逐渐向外扩展。Ⅲ区为小变形区,具有单向压应力、切向以及径向两向拉应力的三向应力状态,纵向易产生开裂。基于此,根据产品特点,制定了三种工艺方案,如图 3所示。
|
图 2 镦锻时的变形 Fig.2 Deformation during upsetting |
|
图 3 六角头成形方案(单位:mm) Fig.3 The forming scheme of hex head:(1) Blank (2) reducing diameter (3) pre upsetting (4) upsetting (a) Scheme 1; (1) Blank (2) reducing diameter (3) pre upsetting (4) upsetting (b) Scheme 2; (1) Blank (2) reducing diameter (3) pre upsetting (4) upsetting (c) Scheme 3 |
工艺优化通常采用正交试验、响应面法、最优化模型等对工艺参数进行优化,而正交试验是根据一个工艺选取多种因素与水平,需要做多种试验,再通过计算获得最优化参数,过程繁琐;响应面法是利用合理的试验设计方法,采用多元二次回归方程来拟合因素与响应值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变量问题的一种统计方法,而本文是多成形方案优化显然是不合适的;最优化模型是根据所求目标,建立合理的数学模型,得到最优的方案。本文采用林新波等[14]提出的评估数学模型,采用有限元仿真技术得到六角球头销的三个不同成形方案的应力、应变、成形载荷、损伤值,获得最佳工艺方案。数学模型如下:
| $ \begin{array}{l} {\rm{min}}{F_j}\left( n \right) = min\mathop \sum \limits_{k = 1, j = 1}^{k = 4, j = m} {w_k}{f_{{\rm{k}}, j(n)}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {k = 1, 2, 3, 4;j = 1, 2 \ldots m} \right) \end{array} $ | (1) |
式中:j为成形工艺方案的序号;k为目标函数的序号;n为成形方案中工序的数目;fk, j(n)为目标函数;wk为目标函数的权值;f1, j(n),f2, j(n),f3, j(n),f4, j(n)为分别为应力分布不均匀度、应变分布不均匀度、载荷分布不均匀度、损伤分布不均匀度。
| $ \begin{array}{l} {f_{{\rm{k}}, j(n)}} = \mathop \sum \limits_{i = 1}^n {\rm{ }}{\left[ {\frac{{{{\left( {{\varphi _{i, j}} - {\varphi _{j - ave}}} \right)}^2}}}{n}} \right]^{1/2}}\left( {k = 1, 2, 3, {\rm{ }}4;} \right.\\ \left. {i = 1, 2 \ldots n;j = 1, 2 \ldots m} \right) \end{array} $ | (2) |
式中:i为成形工艺方案的第i个工序;φi, j为成形工艺方案的某个参数的数值;φj-ave为成形工艺方案的某个参数的平均值。
3 有限元模型的建立根据成形方案建立简易模具,本文采用Solidworks三维软件建模。六角球头销为轴对称零件,为了提高仿真效率,取零件的1/6作为研究对象。在软件中确定冲棒、凸模、凹模、工件之间的装配关系,并分别另存为STL格式后再导入到有限元分析软件DEFORM中。
材料选择软件自带35号钢,设置其为塑形性体,在成形过程中不考虑模具的变形,设置其为刚体。采用剪切模型,划分网格为50 000个四面体单元,步长增量为0.05 mm,初始温度设为20 ℃,摩擦因子为0.12,冲棒速度为100 mm·s-1。
4 工艺优化与有限元分析有限元仿真技术的应用,为成形工艺方案的确定以及优化提供了便利与依据。由于3个方案中,第2工位都为缩径,不作为对比,主要对比工位3与工位4。
4.1 工艺优化表 2为三种成形方案所对应的结果对比,根据结果代入公式(1)优化数学模型,得到表 3所示参数值。
| 表 2 三种成形方案结果对比 Table 2 The results of three forming schemes are compared |
| 表 3 优化模型对应的参数值 Table 3 Optimize the corresponding parameter values of the model |
通过不同的权值计算得到表 4计算结果,可知方案2为最优方案,即锥形成形为六角为最优,其次为预六角形,大V锥形效果最差。
| 表 4 不同权值下的计算结果 Table 4 Calculation results under different weights |
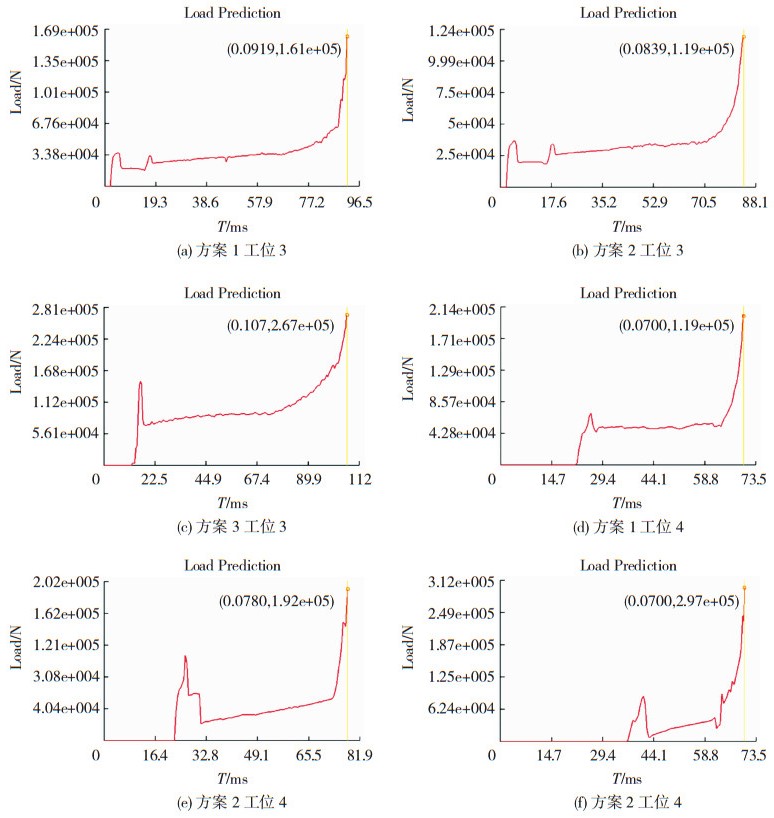
图 4是各方案成形的模具载荷-时间曲线图。从变化规律看可以分为三个阶段,模具与工件接触前阶段、模具与工件接触阶段、成形终了阶段。在接触前阶段由于不发生形变,载荷几乎为零;当开始接触时,载荷迅速上升,随着成形的进行,载荷平稳上升,随着成形终了阶段开始,载荷急剧上升,直到成形完成达到最高值,这与实际相符。
|
图 4 载荷分布 Fig.4 Load distribution:(a) Scheme 1 station 3; (b) scheme 2 Station 3; (c) scheme 3 station 3;(d) Scheme 1 station 4; (e) scheme 2 station 4; (f) scheme 2 station 4 |
图 4(a)、(b)、(c)分别为方案1、2、3的预镦的载荷分布,从图中可以看出,方案2的成形载荷119 kN最小,方案3的成形载荷267 kN最大。从行程来看,方案3所需行程最大,方案1次之,方案2最小。从成形形状来看,方案1成形为大倒锥型,在成形开始时在模具的作用下,载荷缓慢上升,形状缓慢变为锥鼓形,之后成形越来越困难,在锥角处易形成死角,成形困难;方案2成形为锥形,成形过程先在模具的作用下,缓慢由小锥形慢慢成形最后镦锻成形,金属流动合理;方案3成形为锥六角,由于型腔与工件在初期没有接触,所以先成形为锥鼓形,之后在型腔的作用下,成形为锥六角,所需行程较大,载荷也更大。
图 4(d)、(e)、(f)分别为方案1、2、3的镦锻的载荷分布,从图中可以看出,方案2的成形载荷192 kN最小,方案3的成形载荷297 kN最大。由于预成形的形状不一样,导致成形充填模具的过程不一样,成形质量也不一样。方案1由大倒锥型开始成形,先成形底部圆角,再不断往外扩展,当在型腔的作用下上部六角先成形,由于在闭合的型腔中,温度快速上升,载荷也上升,下部六角易产生充填不饱满。方案2由锥形开始成形,在凸模和上冲棒的作用下,工件不断往外伸展,先成形下部的六角,随着模具不断下行,材料由下往上不断填充,最后填充完成,材料流动合理,模具排气顺畅,使用寿命较高。方案3由于预先成形为六角,在开始成形时载荷较小,随着成形终了载荷急剧上升,在上部六角边缘易产生飞边,质量不稳定。
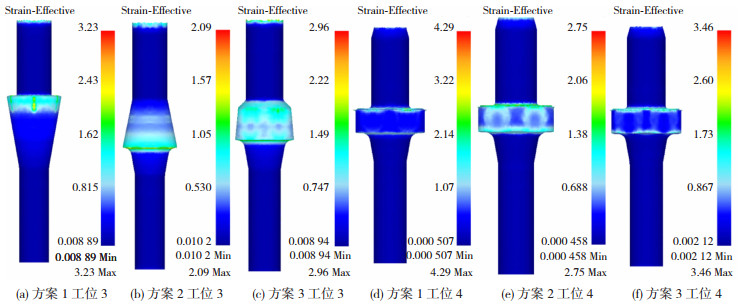
4.3 应变分析应变场是衡量金属塑性变形的重要参数,其可以直观的分析材料在变形中受到的不均匀程度,因此可以判断成形中各种缺陷的产生[15]。图 5为各方案工位的应变分布,从图 5(a)可以看出锥角处应变最大,最大为3.23;图 5(b)中凸模与凹模连接处应变最大,其值为2.09;图 5(c)中外六角处应变最大,其值为2.96;方案2的应变最小。六角成形,根据预成形的形状不同,应变不同,从图 5(d)看出,由大倒锥型成形六角头,应变最大,最大为4.29;由锥形成形六角头,应变最小,最大为2.75,选择方案2成形更为合适。
|
图 5 应变分布 Fig.5 Strain distribution:(a) Scheme 1 station 3; (b) scheme 2 Station 3; (c) scheme 3 station 3; (d) scheme 1 station 4; (e) scheme 2 station 4; (f) scheme 3 station 4 |
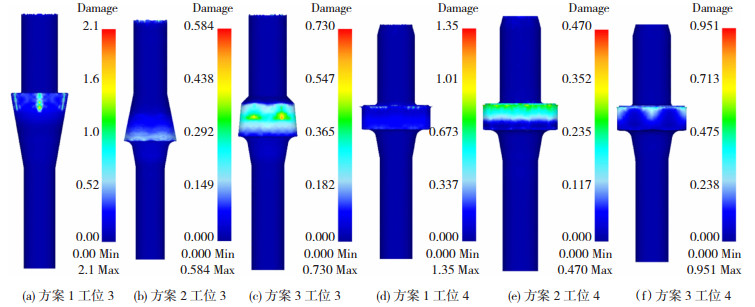
损伤值的大小是反应金属材料成形发生断裂以及破环程度的一个衡量标准[16-17]。图 6为各方案工位的损伤分布,对比工位3的损伤值,方案1损伤值最大为2.1,其次为方案3,方案2损伤值最小为0.584;对比工位4的损伤值,方案1损伤值最大为1.35,其次为方案3,方案2损伤值最小为0.470。
|
图 6 损伤分布 Fig.6 Damage distribution:(a) Scheme 1 station 3; (b) scheme 2 Station 3; (c) scheme 3 station 3; (d) scheme 1 station 4; (e) scheme 2 station 4; (f) scheme 3 station 4 |
工件在成形过程中,易产生死角时,材料不宜易流动,损伤值较大,这与实际生产相符。工位1在形成锥鼓形之后,继续成形,材料不易流动,填充困难,在生产时易产生裂纹、填充不饱满等缺陷。而方案2材料流动合理,损伤值较小,不易产生缺陷,加工质量更好。
综合工艺优化以及有限元模拟结果发现,方案2更为合适,其应力应变、成形载荷、损伤方面最小,不宜易产生成形缺陷,成形质量更为稳定,即采用方案2成形。
5 试验验证生产试验采用JBF-19B-4S冷锻机,如图 7所示,进行六角球头销的冷锻成形试验,采用参考方案2进行模具结构设计,材料为SWRCH35K,毛坯为宝钢Φ6.94的盘条线材,并经过热处理软化、磷化皂化处理。

|
图 7 冷锻机 Fig.7 Cold forging machine |
试验结果如图 8所示,六角头表面质量好、充填饱满、无不良缺陷,证明采用方案2的预锻锥形成形为六角头方案合理,流动流动合理,可指导相关产品生产。

|
图 8 产品图 Fig.8 Product figure |
根据产品结构,基于金属塑性成形理论,利用DEFORM-3D完成了汽车六角球头销六角头成形三种工艺方案的数值模拟,提取了三种方案的成形载荷、应变分布、应力分布、损伤分布,并结合数学优化模型,得到了最优方案,得到的若干结论如下:
1) 针对六角一次成形发生镦锻失稳问题,三种成形方案中采用预成形为锥形,可以得到更好的成形效果。
2) 将有限元模拟获得的数据代入数学优化模型得到方案2最优,与有限元成形效果以及各个方案获得的参数的最优方案相符合,为今后冷锻成形优化提供了参考。
3) 方案2成形载荷较小、材料成形损伤值较小、材料流动合理,成形质量更加稳定。经试验证明,方案2成形六角头充填饱满,无不良缺陷,适合企业生产。为六角头成形提供了一种可行方案,由预成形为锥形再成形为六角头较为合理;其预成形为大V形易生成死角,充填困难;预成形为锥六角形成形载荷大,易产生飞边。
| [1] |
ZHOU J, YU Y, ZENG Q. Analysis and experimental studies of internal voids in multi-wedge cross wedge rolling stepped shaft[J]. International Journal of Advanced Manufacturing Technology, 2014, 72(9-12): 1559-1566. DOI:10.1007/s00170-014-5768-9 |
| [2] |
YUAN W, WANG L, YUAN T.Experimental study on cross wedge rolling process of aluminum alloy material[C].in: 5th International Conference on Advanced Engineering Materials and Technology 5 (AEMT 2015), 2015, 415-422.
|
| [3] |
PATER Z, TOFIL A, TONCZAK J, et al. Numerical analysis of the cross wedge rolling process (CWR) for a stepped shaft[J]. Metalurgija, 2015(54): 177-180. |
| [4] |
WINIARSKI G, GONTARZ A, PATER Z. A new process for the forming of a triangular flange in hollow shafts from Ti6Al4V alloy[J]. Archives of Civil and Mechanical Engineering, 2015(15): 911-916. DOI:10.1016/j.acme.2015.01.001 |
| [5] |
LANDRE J, PERTENCE A, CETLIN P R. On the utilisation of ductile fracture criteria in cold forging[J]. Finite Elements in Analysis and Design, 2003, 39: 175-186. DOI:10.1016/S0168-874X(02)00065-3 |
| [6] |
TOSHIHIKO M, SUYANG L. A new definition of complexity factor of cold forging process[J]. Precision Engineering, 2009, 33: 44-49. DOI:10.1016/j.precisioneng.2008.03.006 |
| [7] |
梁建平, 程旺军. 基于数值模拟的锥形螺母冷镦挤成形分析及模具设计[J]. 锻压技术, 2015, 40(7): 151-155. LIANG Jianping, CHENG Wangjun. Deformation analysis and die design of cold heading extrusion for a conical nut based on numerical simulation[J]. Forging and Stamping Technology, 2015, 40(7): 151-155. DOI:10.13330/j.issn.1000-3940.2015.07.030 |
| [8] |
张臻, 刘三军. 基于Deform 3D的阶梯轴冷锻成形工艺有限元分析[J]. 热加工工艺, 2017, 46(7): 164-166. ZHANG Zhen, LIU Sanjun. Finite Element Analysis of Stepped Shaft Cold Forging Process Based on Deform 3D[J]. Hot Working Technology, 2017, 46(7): 164-166. DOI:10.14158/j.cnki.1001-3814.2017.07.044 |
| [9] |
HU Chengliang, YIN Qiang, ZHAO Zhen. A novel method for determining friction in cold forging of complex parts using a steady combined forward and backward extrusion test[J]. Journal of Materials Processing Tech, 2017, 249: 57-66. DOI:10.1016/j.jmatprotec.2017.06.001 |
| [10] |
王可胜, 陈勇章, 韩豫, 等. 铝合金手机壳冷挤压拉深复合成形工艺及优化[J]. 塑性工程学报, 2015(4): 30-34. WANG Kesheng, CHEN Yongzhang, HAN Yu, et al. Cold Extrusion-drawing composite forming process and optimization for aluminum alloy mobile telephone shell[J]. Journal of Plasticity Engineering, 2015(4): 30-34. DOI:10.3969/j.issn.1007-2012.2015.04.006 |
| [11] |
潘小迎, 汪建敏, 郭嘉晨. 基于微观遗传算法优化法兰滑套成形工艺[J]. 塑性工程学报, 2018, 25(2): 86-90. PAN Xiaoying, WANG Jianmin, GUO Jiachen. Optimization of flange sliding sleeve forming process based on micro-genetic algorithm[J]. Journal of Plasticity Engineering, 2018, 25(2): 86-90. DOI:10.3969/j.issn.1007-2012.2018.02.013 |
| [12] |
吴先洋. 基于响应面法的整体式结合齿齿轮温锻工艺优化[J]. 锻压技术, 2018, 43(8): 27-34. WU Xianyang. Optimization on warm forging process for monoblock combined tooth gear based on response surface method[J]. Forging and Stamping Technology, 2018, 43(8): 27-34. DOI:10.13330/j.issn.1000-3940.2018.08.006 |
| [13] |
陈剑, 张东民, 周伟民, 等. 锥鼓形冷镦成形球头的工艺参数优化[J]. 锻压技术, 2017, 42(10): 5-8, 12. CHEN Jian, ZHANG Dongmin, ZHOU Weimin, et al. Optimization of process parameters on cone-drum ball head in cold upsetting[J]. Forging and Stamping Technology, 2017, 42(10): 5-8, 12. DOI:10.13330/j.issn.1000-3940.2017.10.002 |
| [14] |
林新波, 李荣先, 柳百成, 等. 基于数值模拟的工艺评估与优化[J]. 塑性工程学报, 2005, 12(1): 58-63. LIN Xinbo, LI Rongxian, LIU Baicheng, et al. Process evaluation and optimization based on numerical simulation[J]. Journal of Plasticity Engineering, 2005, 12(1): 58-63. DOI:10.3969/j.issn.1007-2012.2005.01.014 |
| [15] |
张东民, 盛育东, 张金玉, 等. 六角开槽螺母的冷镦工艺优化及数值模拟[J]. 机械设计与制造, 2018(3): 191-194. ZHANG Dongmin, SHENG Yudong, ZHANG Jinyu, et al. Numerical simulation and optimization for cold heading of hexagonal slot nut[J]. Machinery Design & Manufacture, 2018(3): 191-194. DOI:10.19356/j.cnki.1001-3997.2018.03.057 |
| [16] |
陈学文, 王进, 陈军, 等. 基于最小损伤值的齿轮毛坯锻造成形过程工艺参数优化设计[J]. 上海交通大学学报, 2005(7): 1070-1072. CHEN Xuewen, WANG Jin, CHEN Jun, et al. The technological parameter optimization of gear billet hot forging process with damage minimization[J]. Journal of Shanghai Jiaotong University, 2005(7): 1070-1072. DOI:10.16183/j.cnki.jsjtu.2005.07.010 |
| [17] |
肖志玲, 刘百宣, 刘华, 等. 螺旋道钉多工位冷镦成形工艺优化及数值模拟[J]. 锻压技术, 2014, 39(2): 79-83. XIAO Zhiling, LIU Baixuan, LIU Hua, et al. Process optimization and numerical simulation of multi-stage cold heading for railway screw spike[J]. Forging and Stamping Technology, 2014, 39(2): 79-83. DOI:10.13330/j.issn.1000-3940.2014.02.016 |
 2020, Vol. 28
2020, Vol. 28


