非晶合金是由特定组分的熔融金属超急冷凝固形成的一种原子短程有序、长程无序的新型材料[1-3]。与晶态合金相比,非晶合金由于其内部没有位错、晶界等缺陷而具有高强度、高硬度、高弹性极限以及优异磁性、耐磨性和耐蚀性[4-6],可广泛应用于减震零件、磁性零件、体育用品、医疗器械等方面[7]。
非晶合金常温下为脆性材料,几乎不发生塑性变形,但将其加热至过冷液相区后(温度高于非晶合金的玻璃转变温度Tg,但低于晶化温度Tx),合金会从脆性状态转变为黏性状态,表现出良好的塑性变形能力。温度越高,非晶合金黏度越低,塑性越好,成形性能也越好,因此,非晶合金构件多采用热塑性成形[8-12]。为优化非晶合金热塑性成形工艺参数,对非晶合金在过冷液相区内的流变行为的研究就显得尤为重要。最初,Hey[13]研究了钯基非晶合金在过冷液相区内的应变速率与稳态流变应力的对应关系。Kato[14]基于此研究了动力学黏度与应变速率的关系,提出了应力弛豫本构模型(Stress Relaxation Function),但该模型只能描述应变速率与黏度之间的关系,局限性较大。随后,Johnson[15]系统地研究了锆基非晶合金在过冷液相区内(1.1Tg)的流变行为,根据Vogel-Fuleher-Tamrnan黏度流变方程与自由体积模型,建立了自恰动力学自由体积模型(Self-Consistent Dynamic Free Volume Model),该模型从理论层面分析了非晶合金变形过程中试样内部自由体积含量的变化,但该模型无法具体描述非晶合金的热塑性流变行为。Lu[16]基于经典的麦克斯韦粘弹性模型(Maxwell Viscoelastic Model)理论,提出虚应力模型(Fictive Stress Model),该模型可有效预测非晶合金在过冷液相区较低应变速率下的稳态流动应力。Wang[17]提出的Maxwell-Pulse本构模型描述了Zr基非晶合金在低应变速率下的流变行为,模型耦合了表征蠕变应力的Maxwell模型和表征应力过冲峰的Pulse双指数函数模型。上述模型大多基于低应变速率下(≤10-2/s)的实验数据建立。目前,由于低速变形时间较长,非晶合金构件成形时存在严重的氧化现象,严重影响表面质量,而且为了避免发生晶化,成形温度通常较低(1.1Tg),不利于发挥非晶合金的塑性能力。与之相反,非晶合金在更高应变速率下成形,可大幅缩短成形时间,使材料在更高温度下成形,展现出较好的塑性能力,并仍能保持非晶态,因此,非晶合金在较高速率下成形日益受到关注[18-23]。然而,目前的研究主要是针对非晶合金在应变速率为(10-5~10-2)/s时的流变行为进行的,而对于更高温度和更高应变速率下非晶合金的流变行为与本构模型的研究尚未见报道。
本文将针对Zr35Ti30Cu8.25Be26.75非晶合金在过冷液相区内较高温度(1.2Tg)和较高应变速率((10-2~100)/s)下的流变行为进行系统研究,并探索建立可同时准确描述其牛顿流变及非牛顿流变行为的本构模型,以期为Zr35Ti30Cu8.25Be26.75合金高速成形的有限元模拟及工艺参数选取提供基础数学模型。
1 实验采用真空电弧炉熔炼法制备成分为Zr35Ti30Cu8.25Be26.75的母合金。熔炼前,熔炼室抽真空至真空度达到6×10-3 Pa后,向炉内充入高纯氩气,而后开始熔炼。首先将炉内的海绵钛反复熔炼数次以保证炉内氧气耗尽,然后开始熔炼试样,将试样在电磁搅拌的辅助下反复熔炼5次,以确保合金成分的均匀性和准确性。随后将炼好的母合金放入试管内,在感应炉中熔化后喷入铜模中急冷成形得到直径3 mm的圆柱形棒材。采用X射线衍射仪(XRD-7000)和差示扫描量热仪(NETZSCH STA449F3)进行非晶合金结构和热性能的表征,确定试样为完全非晶态结构,其玻璃转变温度为581 K,晶化温度为723 K,过冷液相区宽度为142 K。
根据ASTM E9-89a(2000)金属材料压缩实验标准中的推荐值,本文选择1.5 :1的高径比,用切片机将试样切成Φ3 mm×4.5 mm的圆柱形试样。为确保试样两端面平行度良好且表面光滑,切削过程在冷却液辅助下进行。采用Zwick/Roell力学性能实验机进行压缩实验,温度波动范围为±2 K。实验温度选择为633、653、673、683、693 K,应变速率选择为2×10-2、5×10-2、2×10-1、5×10-1、2×102、3×102 s-1,变形量为60%。实验设备加热至设定温度后保温2 h,以确保模具温度均匀,然后将试样放于模具上,保温5 min后开始压缩实验。为保证实验结果的准确性和可重复性,每组实验至少重复3次。
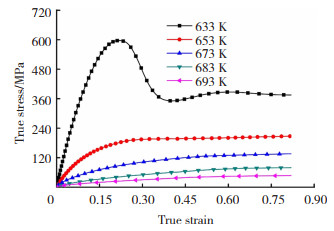
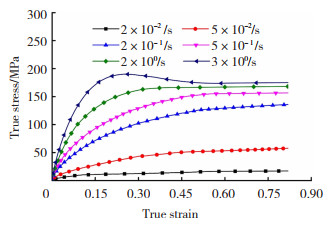
2 结果与讨论 2.1 实验结果Zr35Ti30Cu8.25Be26.75非晶合金在过冷液相区内的应力-应变曲线如图 1、2所示。由图 1可见,材料的流变应力随温度的升高而减小。当变形温度较低时,应力-应变曲线在变形起始阶段出现峰值应力现象[24](Stress Overshoot)。当流变应力达到峰值后迅速下降并进入一个平缓的稳定阶段,流变应力不再随应变的增加而变化。而当变形温度较高时,流变应力随应变的增加逐渐增加,直至到达稳态应力。在633 K以2×10-1/s的速率压缩时的曲线,在应力过冲峰后并未直接下降到稳态应力,而是出现了低于稳态应力的现象,然后才逐渐趋于稳态。在更高温度或更低应变速率下的曲线均未出现这一现象。文献[25]指出,应力-应变曲线出现振荡主要与应变速率软化相关,即随着应变速率的增加,非晶合金达到稳态流动的时间比非晶合金内部自由体积完成弛豫所需时间短,此时会出现应变速率软化和振荡现象。图 2中,在恒定温度下,随着应变速率的增加,试样的流变应力单调增加。应变速率较低时表现为牛顿流变,当应变速率增至(2×100~3×100)/s后,非晶合金变形由牛顿流变转变为非牛顿流变。
|
图 1 Zr35Ti30Cu8.25Be26.75非晶合金在应变速率为2×10-1/s时,不同温度下的应力-应变曲线 Fig.1 Stress-strain curve of Zr35Ti30Cu8.25Be26.75 amorphous alloy at different temperatures at a strain rate of 2×10-1/s |
|
图 2 Zr35Ti30Cu8.25Be26.75非晶合金在673 K时,不同应变速率下的应力-应变曲线 Fig.2 Stress-strain curve of Zr35Ti30Cu8.25Be26.75 amorphous alloy at different strain rates at 673 K |
根据实验所得非晶合金试样的应力-应变曲线,用式(1)计算Zr35Ti30Cu8.25Be26.75非晶合金试样在不同温度下压缩变形的黏度。
| $ \eta = {\sigma _{{\rm{flow}}}}/3\dot \varepsilon $ | (1) |
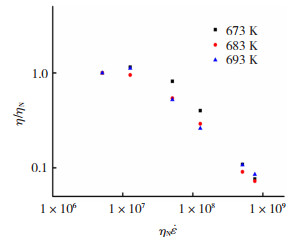
非晶合金在过冷液相区内不同温度和应变速率下的黏度可表示为一条通用曲线,以每一温度下牛顿黏度ηN(即低应变速率条件下的η)为基准,将压缩实验测出的表观黏度进行归一化处理,即η/ηN,如图 3所示。在实验温度范围内的牛顿黏度与Arrhenius型方程吻合得很好,可表示为
| $ {\eta _{\rm{N}}} = B{\rm{exp}} (H/RT) $ | (2) |
|
图 3 Zr35Ti30Cu8.25Be26.75非晶合金在不同温度下的黏度归一化曲线 Fig.3 Normalized curve of viscosity of Zr35Ti30Cu8.25Be26.75 amorphous alloy at different temperatures |
式中:H为进入粘滞流变状态的激活能;B为结构因子;R为气体常数。通过对平衡黏度公式的计算得到:H=205.56 kJ/mol,B=2.23×10-8。
由图 3可知,不同温度的黏度归一化曲线形成一条折线,拐点就是牛顿流变和非牛顿流变的转折点。在较高温度较低应变速率下,试样的黏度值随应变速率的变化很小,表现为牛顿流变,其主要原因为:在较高温度较低应变速率下,试样内部流动单元由热平衡时的单个运动到相互关联成集体的时间长于结构弛豫时间,并且流动单元开动的时间间隔也长于焓弛豫时间,此时变形软化的效果低于压应力导致的致密化,因此,黏度几乎不发生变化,试样随着流动单元的开动达到稳态流动。而应变速率较高时黏度值随应变速率的变化出现较大变化,表现为非牛顿流变,其主要原因为:变形过程中试样的焓弛豫时间长于流动单元开动的时间间隔,此时变形软化效应大于压应力导致的致密化,流动单元浓度增加,因此,过冷液体黏度降低。
2.3 虚应力本构建模Lu[16]在对锆基非晶合金的高温变形研究中提出了虚应力模型,该模型在较低应变速率(≤10-2/s)下能较好地拟合非晶合金在过冷液相区内的稳态流动,模型预测结果与实验结果一致性良好,且模型参数少,有效简化了计算过程。但该模型对非晶合金在过冷液相区内较高应变速率下(>10-2/s)的流变行为的预测效果尚不明确,因此,本文将对Zr35Ti30Cu8.25Be26.75非晶合金在过冷液相区内的高速压缩实验数据进行虚应力本构的拟合。
图 3所示不同温度的黏度归一化曲线在非牛顿流变阶段并不重合,需要乘以一个转移因子,使不同温度下的黏度归一化曲线重新合成一条曲线,该转移因子为αT,其计算公式如式(3)所示。
| $ {\alpha _{\rm{T}}} = {\dot \varepsilon _m}/\dot \varepsilon $ | (3) |
式中:
| $ {\alpha _{\rm{T}}} = C{\rm{exp}} \left( {\frac{{{H^*}}}{{RT}}} \right) $ | (4) |
式中:H*为进入粘滞流变状态的激活能;C为结构因子;R为气体常数。归一化后的主曲线可以表示为
| $ \frac{\eta }{{{\eta _{\rm{N}}}}} = 1 - {\rm{exp}}\left( {\frac{{ - 1}}{{t{\eta _{\rm{N}}}{{\dot \varepsilon }_{\rm{m}}}}}} \right) $ | (5) |
式中:ηN为牛顿黏度;t为与应变速率有关的常数。结合式(1),虚应力本构模型可以表示为
| $ {\sigma _{{\rm{flow}}}} = 3\dot \varepsilon B{\rm{exp }}\left( {\frac{H}{{RT}}} \right)\left\{ {1 - {\rm{exp}}\left[ {\frac{{ - 1}}{{tC{\rm{exp}} \left( {\frac{{{H^*}}}{{RT}}} \right)\dot \varepsilon }}} \right]} \right\} $ | (6) |
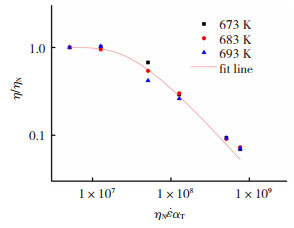
图 4是经过归一化后利用转移因子转换得到的数值点。利用式(5)对图中数值点进行拟合,可得到式(5)中参数的数值,如表 1所示。从图 4可以看到,拟合曲线可较好地吻合数值点。
|
图 4 Zr35Ti30Cu8.25Be26.75非晶合金归一化后的拟合主曲线 Fig.4 The fitted main curve of Zr35Ti30Cu8.25Be26.75 bulk amorphous alloy after normalization |
| 表 1 虚应力模型各参数的拟合数值 Table 1 The parameters of the Fictive Stress Model |
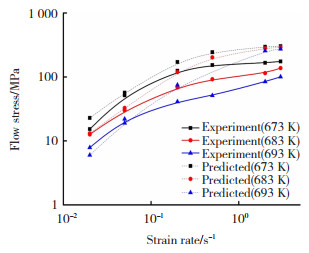
根据模拟方程计算试样在不同温度和应变速率下的稳态流动应力。计算结果如图 5所示,可见,采用虚应力模型表征时,材料的稳态流变应力在低应变速率下(< 10-1/s)拟合效果较好,随着应变速率的增加(>10-1/s),拟合结果与实际结果偏差变大(>50%),模型预测效果较差,且该模型无法反映材料的非牛顿流变现象,因此,不能准确表征Zr35Ti30Cu8.25Be26.75非晶合金在较高应变速率下的流变行为。
|
图 5 Zr35Ti30Cu8.25Be26.75非晶合金在不同温度和应变速率下的稳态流动应力模型预测结果与实验结果对比 Fig.5 Comparison of prediction results and experiment results of steady-state flow stress model of Zr35Ti30Cu8.25Be26.75 amorphous alloy at different temperatures and strain rates |
Wang[17]通过耦合蠕变应力函数模型和脉冲函数模型提出了Maxwell-Pulse模型。其中蠕变应力函数模型(Maxwell)模型可有效描述非晶合金在过冷液相区内的稳态流变行为,双指数型Pulse模型可有效描述非晶合金在过冷液相区的应力过冲现象。但该模型目前主要用于表征非晶合金在过冷液相区内较低应变速率下(≤10-2/s)的变形行为,其对非晶合金在过冷液相区内高温高速变形过程的表征效果尚待研究。
Maxwell-Pulse完整的本构方程表达式为
| $ \begin{array}{*{20}{l}} {\sigma = {\sigma _{\rm{f}}}\left[ {1 - \exp \left( {\frac{{ - \varepsilon }}{{{\tau _{\rm{f}}}\dot \varepsilon }}} \right)} \right] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\sigma _{\rm{p}}}{{\left[ {1 - \exp \left( { - \frac{\varepsilon }{{{t_1}}}} \right)} \right]}^p}\exp \left( { - \frac{\varepsilon }{{{t_2}}}} \right)} \end{array} $ | (7) |
式中:σf为稳态流动应力;σp为过冲峰值应力;τf为应力弛豫时间;t1和t2分别是前沿半高宽和后沿半高宽,其具体表达式如下。
| $ {{\sigma _{\rm{f}}} = 3\dot \varepsilon B{\rm{exp}}\left( {\frac{H}{{RT}}} \right)\left\{ {1 - \exp \left[ {\frac{{ - 1}}{{tC\exp \left( {\frac{{{H^*}}}{{RT}}} \right)\dot \varepsilon }}} \right]} \right\}} $ | (8) |
| $ {{\sigma _{\rm{p}}} = K\dot \varepsilon \exp \left( {\frac{{{H^\prime }}}{{RT}}} \right)} $ | (9) |
| $ {\tau _{\rm{f}}} = \frac{{{\sigma _{\rm{f}}}}}{{3E\dot \varepsilon }} $ | (10) |
根据Zr35Ti30Cu8.25Be26.75非晶合金在不同温度和不同应变速率下的压缩实验结果,进行应力-应变曲线数据回归分析,得到式(7)中各参数的拟合值,代入后式(7)可表示为
| $ \begin{array}{l} \sigma = 3.24 \times {10^{ - 8}}\dot \varepsilon \exp \left( {\frac{{213.21}}{{RT}}} \right)\left\{ {1 - \exp \left[ {\frac{{ - 1}}{{1.64 \times {{10}^{ - 16}}\exp \left( {\frac{{213.21}}{{RT}}} \right)\dot \varepsilon )}}} \right]} \right\}\left[ {1 - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \exp \left( { - 9.24 \times {{10}^{ - 8}}E\varepsilon \dot \varepsilon \exp \left( {\frac{{213.21}}{{RT}}} \right)\left\{ {1 - \exp \left[ {\frac{{ - 1}}{{1.64 \times {{10}^{ - 16}}\exp \left( {\frac{{213.21}}{{RT}}} \right)\dot \varepsilon }}} \right]} \right\}} \right)} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.786 \times {10^{ - 5}}\dot \varepsilon \exp \left( {\frac{{77.417}}{{RT}}} \right){[1 - \exp ( - 48.077\varepsilon )]^{45.99}}\exp ( - 71.43\varepsilon ) \end{array} $ | (11) |
表 2列出了Zr35Ti30Cu8.25Be26.75块体非晶合金Maxwell-Pulse本构模型的基本材料参数的具体拟合结果,各参数的拟合相关性系数均在0.92以上。
| 表 2 Zr35Ti30Cu8.25Be26.75非晶合金Maxwell-Pulse本构模型的基本材料参数 Table 2 Basic material parameters of the Maxwell-Pulse constitutive model of Zr35Ti30Cu8.25Be26.75 amorphous alloy |
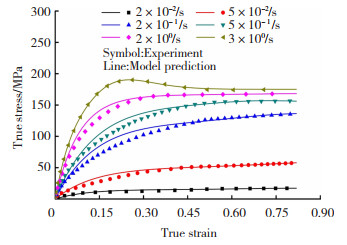
将Maxwell-Pulse本构模型预测的应力-应变曲线与实验应力-应变曲线进行对比,结果如图 6、7所示,图中离散点表示实验结果,实线为拟合结果。
|
图 6 Zr35Ti30Cu8.25Be26.75非晶合金在673 K不同应变速率下的实验曲线与模型预测曲线 Fig.6 Experimental curves and model prediction curves of Zr35Ti30Cu8.25Be26.75 amorphous alloy at different strain rates and 673 K |

|
图 7 Zr35Ti30Cu8.25Be26.75非晶合金在2×10-1/s不同温度下的实验曲线与模型预测曲线 Fig.7 Experimental curves and model prediction curves of Zr35Ti30Cu8.25Be26.75 amorphous alloy at different temperatures and 2×10-1/s |
从图 6和图 7可以发现:图 6中673 K时所有应变速率对应的曲线及图 7中633 K温度以上的所有曲线,其拟合值与实验值的一致性良好,经统计其偏差均在10%以内;仅633 K下2×10-1/s对应的曲线,由于出现了振荡,在应力峰值后的振荡区域拟合值与实验值出现稍大偏差(≤15.5%),但对于峰值应力和稳态应力等特征值的预测效果仍较好(偏差 < 3%)。可见,Maxwell-Pulse本构模型对应力-应变曲线的的整体预测效果较好,且能反映Zr35Ti30Cu8.25Be26.75非晶合金在不同条件下呈现的不同的变形行为,包括牛顿流变和非牛顿流变。研究结果表明,Maxwell-Pulse模型在Zr35Ti30Cu8.25Be26.75非晶合金高温和较高应变速率变形条件下适用性较好。
3 结论1) Zr35Ti30Cu8.25Be26.75非晶合金的稳态流变应力在过冷液相区内随温度的升高而减小,随应变速率的升高而增大。
2) 随着温度的降低或应变速率的增大,Zr35Ti30Cu8.25Be26.75非晶合金的变形机制会由牛顿流变转变为非牛顿流变。
3) 在高温较高应变速率变形条件下,Maxwell-Pulse本构模型能够准确表征Zr35Ti30Cu8.25Be26.75非晶合金的应力应变关系,较好地反映材料在压缩变形过程中的应力过冲现象。
| [1] |
SHAMLAYE K F, LAWS K J, LÖFFLER J F. Exceptionally broad bulk metallic glass formation in the Mg-Cu-Yb system[J]. Acta Materialia, 2017, 128: 188-196. DOI:10.1016/j.actamat.2017.02.013 |
| [2] |
HUFNAGEL T C, SCHUH C A, FALK M L. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments[J]. Acta Materialia, 2016, 109: 375-393. DOI:10.1016/j.actamat.2016.01.049 |
| [3] |
BORDEENITHIKASEM P, LIU J, KUBE S A, et al. Determination of critical cooling rates in metallic glass forming alloy libraries through laser spike annealing[J]. Scientific Reports, 2017, 7(1): 7155. DOI:10.1038/s41598-017-07719-2 |
| [4] |
INOUE A, TAKEUCHI A. Recentdevelopment and application products of bulk glassy alloys[J]. Acta Materialia, 2011, 59(6): 2243-2267. DOI:10.1016/j.actamat.2010.11.027 |
| [5] |
SUN Y, CONCUSTELL A, GREER A L. Thermomechanical processing of metallic glasses: extending the range of the glassy state[J]. Nature Reviews Materials, 2016, 1(9): 16039. DOI:10.1038/natrevmats.2016.39 |
| [6] |
李锐阳, 袁子洲, 康健, 等. 冷却速率对(Zr56Co28Al16)98Y2非晶合金显微结构和力学性能的影响[J]. 机械工程材料, 2016, 40(5): 20-24. LI Ruiyang, YUAN Zizhou, KANG Jian, et al. Effect of cooling rate on microstructure and mechanical properties of amorphous alloy (Zr56Co28Al16)98Y2[J]. Mechanical Engineering Materials, 2016, 40(5): 20-24. DOI:10.11973/jxgccl201605003 |
| [7] |
GHIDELLI M, IDRISSI H, GRAVIER S, et al. Homogeneous flow and size dependent mechanical behavior in highly ductile Zr65Ni35 metallic glass films[J]. Acta Materialia, 2017, 131: 246-259. DOI:10.1016/j.actamat.2017.03.072 |
| [8] |
雷现奇, 魏宇杰. 金属非晶的强度和变形特性[J]. 固体力学学报, 2016, 37(4): 312-339. LEI Xianqi, WEI Yujie. Strength and deformation properties of metallic amorphous[J]. Journal of Solid Mechanics, 2016, 37(4): 312-339. |
| [9] |
WANG J Q, SHEN Y, PEREPEZKO J H, et al. Increasing the kinetic stability of bulk metallic glasses[J]. Acta Materialia, 2016, 104: 25-32. DOI:10.1016/j.actamat.2015.11.048 |
| [10] |
LI N, CHEN W, LIU L. Thermoplastic micro-forming of bulk metallic glasses: areview[J]. JOM, 2016, 68(4): 1246-1261. DOI:10.1007/s11837-016-1844-y |
| [11] |
ZHANG Q, WANG L, ZHAO Y, et al. Remarkable improving plasticity of a brittle Zr-based bulk metallic glass by a high rheological rate forming method in centesimal seconds[J]. Materials Letters, 2016, 164: 348-352. DOI:10.1016/j.matlet.2015.11.017 |
| [12] |
YAO Z F, QIAO J C, PELLETIER J M, et al. High temperature deformation behaviors of the Zr63.36Cu14.52Ni10.12Al12 bulk metallic glass[J]. Journal of Materials Science, 2016, 51(8): 4079-4087. DOI:10.1007/s10853-016-9729-6 |
| [13] |
HEY P D, SIETSMA J, BEUKEL A V D. Structural disordering in amorphous Pd40Ni40P20 induced by high temperature deformation[J]. Acta Materialia, 1998, 46(16): 5873-5882. DOI:10.1016/s1359-6454(98)00234-1 |
| [14] |
KATO H, KAWAMURA Y, INOUE A, et al. Newtonian to non-Newtonian master flow curves of a bulk glass alloy Pd40Ni10Cu30P20[J]. Applied Physics Letters, 1998, 73(25): 3665-3667. DOI:10.1063/1.122856 |
| [15] |
JOHNSON W L, LU J, DEMETRIOU M D. Deformation and flow in bulk metallic glasses and deeply undercooled glass forming liquids-a self consistent dynamic free volume model[J]. Intermetallics, 2002, 10(11-12): 1039-1046. DOI:10.1016/s0966-9795(02)00160-7 |
| [16] |
LU J, RAVICHANDRAN G, JOHNSON W L. Deformation behavior of the Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass over a wide range of strain-rates and temperatures[J]. Acta Materialia, 2003, 51(12): 3429-3443. DOI:10.1016/s1359-6454(03)00164-2 |
| [17] |
WANG X, TANG N, ZHENG Z, et al. A Maxwell-pulse constitutive model of Zr55Cu30Al10Ni5 bulk metallic glasses in supercooled liquid region[J]. Journal of Alloys and Compounds, 2011, 509(5): 2518-2522. DOI:10.1016/j.jallcom.2010.11.070 |
| [18] |
VIVEK A, TABER G A, JOHNSON J R, et al.Vaporizing foil actuator: a tool for creating high-pressure impulses for metalworking[M].60 Excellent Inventions in Metal Forming. Springer Berlin Heidelberg, 2015. DOI: 10.1007/978-3-662-46312-3_12
|
| [19] |
VIVEK A, PRESLEY M, FLORES K M, et al. Solid state impact welding of BMG and copper by vaporizing foil actuator welding[J]. Materials Science and Engineering: A, 2015, 634: 14-19. DOI:10.1016/j.msea.2015.03.012 |
| [20] |
KALTENBOECK G, DEMETRIOU M D, ROBERTS S, et al. Shaping metallic glasses by electromagnetic pulsing[J]. Nature Communications, 2016, 7: 10576. DOI:10.1038/ncomms10576 |
| [21] |
XIAO Wu, LI Jianjun, ZHENG Zhizhen, et al. The effect of forming speed on the formability of a Zr-based bulk metallic glass[J]. Advanced Materials Research, 2015, 1088: 265-271. DOI:10.4028/www.scientific.net/AMR.1088.265 |
| [22] |
JUN H. Temperature effects on mechanical properties, deformation behavior and formability of Zr-Ti-Cu-Ni-Be-Nb bulk metallic glass composite[J]. Metals and Materials International, 2008, 14(3): 297-306. DOI:10.3365/met.mat.2008.06.297 |
| [23] |
JOHNSON W L, KALTENBOECK G, DEMETRIOU M D, et al. Beating crystallization in glass-forming metals by millisecond heating and processing[J]. Science, 2011, 332(6031): 828-833. DOI:10.1126/science.1201362 |
| [24] |
KAWAMURA Y, SHIBATA T, INOUE A, et al. Stress overshoot in stress-strain curves of Zr65Al10Ni10Cu15 metallic glass[J]. Applied Physics Letters, 1997, 71(6): 779-781. DOI:10.1063/1.119643 |
| [25] |
ZHANG Meng, LIU Lin, WU Yue. Facilitation and correlation of flow in metallic supercooled liquid[J]. The Journal of Chemical Physics, 2013, 139(16): 164508. DOI:10.1063/1.4826318 |
 2020, Vol. 28
2020, Vol. 28


