2. 四川建筑职业技术学院 交通与市政工程系,成都 610500
2. Department of Transport and Municipal Engineering, Sichuan College of Architectural Technology, Chengdu 610399, China
Q345钢因其良好的焊接性能和力学性能,在建筑业、制造业以及特种加工等方面被广泛应用。而平板焊接也是常用的钢结构连接方式,具有连接简单、适用广泛、焊缝强度高、密封性能好等工业特点[1]。在Q345钢平板焊接作业中,焊接接头受热易发生内部组织变化,不可避免地有内部应力残余[2]。残余应力过大会导致构件尺寸形状变形以及脆性增大,在实际应用中存在较大的承载失稳风险[3],因此,减小焊接残余应力是焊接工程中的重要课题。
焊接工艺参数指影响焊接结果的各物理量,直接影响焊接残余应力,因此,可通过考察焊接工艺参数对焊接残余应力的影响情况,选取焊接工艺参数范围以减小焊接残余应力,提高平板结构构件的承载能力,消减工程隐患以及事故发生几率。目前,国内外学者已开展了诸多不同焊接工艺参数与平板焊接残余应力的关系研究。Rybicki等[4]发现焊道数与焊接残余应力之间存在影响关系,设计出相关的计算模型,但在焊道数过多时计算应力会有较大偏差。钱海盛等[5]研究发现,平板焊接残余应力与焊接电压、焊接电流之间均成正比关系,但其分析时仅采用了单因素分析,关系不准确。Wang[6]等研究了焊接速度对焊接接头组织和力学性能的影响,结果显示,随着焊接速度的增加,焊接接头的晶界偏析程度增大,残余应力增大,而拉伸强度会在一定范围内降低,但并未给出焊接速度与残余应力的具体关系规律。Balakrishnan等[7]开展了不同焊接方法对焊接残余应力分布的影响研究,通过仿真计算得出,在一定的焊接速度条件下,埋弧焊的纵向残余应力峰值要低于氩弧焊的应力峰值,但涉及的焊接方法尚有欠缺。蒲晓薇[8]运用有限元算法研究了焊接热输入对Q345钢平板焊接接头应力场的影响,分析表明,焊接热输入的增加导致最大残余应力小范围增大。现有的研究还涉及焊接顺序、焊接层间温度等多项焊接工艺参数[9-12],虽然已有研究通过数值模拟预测了平板焊接残余应力的分布情况,但未对平板焊接残余应力与焊接工艺参数之间的规律进行较细致的定义,且缺乏复数项工艺参数综合影响的分析。
为实现多项焊接工艺参数对Q345钢平板焊接残余应力的综合影响规律研究,得到更简洁、准确的关系模型,本文进行了焊接模拟分析,研究了焊接速度和焊接层间温度与平板横向残余应力和厚度方向残余应力的关系。通过考察多因素分析方法,采用精度较高的二元回归分析法得出焊接残余应力拟合函数,并按照拟合模型中横向和厚度方向残余应力的综合变化趋势优化焊接工艺参数,以期对Q345钢平板焊接作业起到一定的指导作用。
1 Q345钢平板焊接模型 1.1 平板焊接热源与本构模型平板焊接过程中温度场的变化会导致热影响区的力学性能改变,因此,研究平板焊接残余应力必须对焊接热过程进行分析。根据文献调研,平板焊接时在焊缝形成的温度场可由Goldak等[13]提出的双椭球热源模型进行模拟,双椭球模型由前后两部分组成,不同的温度梯度与焊接时的焊丝前后温度场分布情况相符合,热源模型沿z轴运移焊丝,产生的前、后椭球热源模型数学表达式为
| $ q_{1}(x, y, z)=\frac{6 \sqrt{3} f_{1} q_{0}}{a b c_{1} \pi^{3 / 2}} \exp \left[-3\left(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c_{1}^{2}}\right)\right] $ | (1) |
| $ q_{2}(x, y, z)=\frac{6 \sqrt{3} f_{2} q_{0}}{a b c_{2} \pi^{3 / 2}} \exp \left[-3\left(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c_{2}^{2}}\right)\right] $ | (2) |
式中:q1、q2分别为前、后椭球热源模型的内部焊接热流密度,W/mm2; f1、f2为双椭球热源模型函数前后部分的能量分布系数; q0为焊接热输入,J/mm; a、b、c1、c2为热源模型的几何参数,mm。
在实际现场中,Q345钢的平板焊接作业主要为药芯焊丝半自动焊(FCAW-S),焊接电弧的热传导过程可由以下数学式表达[14]。
| $ \rho_{T} c_{T} \frac{\partial T}{\partial t}-\lambda_{T}\left[\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}}\right)\right]=\frac{\partial Q}{\partial t} $ | (3) |
式中:T为t时刻(x, y, z)点处的温度,K; Q为单位体积的热源,J/m3; ρT为密度,kg/m3; λT为导热系数,W/(m2·K); cT为比热容,J/(kg·K)。
平板焊接在热传导过程发生组织变化,局部塑性变形导致应力应变的产生,运用广义胡克定律给出平板焊接的应力-应变关系[15],其本构方程为
| $ \begin{array}{l} \mathrm{d} \sigma_{k k}=\frac{E}{(1-2 v)}\left(\mathrm{d} \varepsilon_{k k}-3 \mathrm{~d} \varepsilon^{t h}\right)+\frac{\mathrm{d} E}{E} \sigma_{k k} \\ \mathrm{~d} s_{i j}=\frac{E}{(1+v)} \mathrm{d} e_{i j}^{\mathrm{e}}+\frac{\mathrm{d} E}{E} s_{i j} \\ \mathrm{~d} \varepsilon^{t h}=\frac{\mathrm{d} \varepsilon^{t h}}{\mathrm{~d} T} \mathrm{~d} T=\alpha_{t} \mathrm{~d} T \end{array} $ | (4) |
式中:σkk为应力张量,MPa; sij为应力偏张量,MPa; E为杨氏模量,GPa; υ为泊松比; εkk为总体应变; εth为热应变; eije为弹性应变偏张量; αt为热应变系数。
1.2 Q345钢平板焊接有限元模型选取8 mm厚Q345钢板进行焊接实验,将两对接的平板用夹具固定两边界四角的区域,在焊接过程中逐渐变为一端固定一端游动,避免板材发生大变形影响焊缝质量[16]。若采用大平板进行焊接实验,为避免焊接产生过大变形,须将平板均分成若干段,每一段进行多层多道焊接[17]。根据焊接接头的实际焊缝结构模拟焊缝区和热影响区的结构,如图 1(a)所示,并据此建立平板多层多道焊接的有限元模型,总体尺寸为300 mm×200 mm×8 mm,模型见图 1(b)。焊接产生的残余应力集中在平板焊接接头处,热影响区主要在焊缝中心距离10 mm范围内。

|
图 1 平板焊接焊缝结构与焊接模型 Fig.1 Plate welded joint structure and welding model: (a) plate welded joint structure; (b) plate welding model |
Q345钢平板焊接现场作业以药芯焊丝半自动焊为主,试验平板的焊缝结构由1道根焊、2道填充焊以及1道盖面焊组成,焊接工艺参数如表 1所示。
| 表 1 焊接工艺参数 Table 1 The welding parameters |
焊接工艺参数中焊接线能量和焊接层间温度是影响焊接残余应力的重要参数。不同焊接线能量造成焊缝和热影响区的热输入变化,影响金属的组织性能,焊接线能量的数学表达式为
| $ Q=60 \eta U I / v $ | (3) |
式中:η为焊接热效率; U为焊接电压,V; I为焊接电流,A; v为焊接速度,mm/min。
分析式(3)可知,焊接线能量主要与焊接电压、焊接电流和焊接速度相关,同等数值变化梯度下焊接速度对焊接线能量的影响与焊接电压和焊接电流作用效果相反。在以焊接速度为参量的前提下,可通过调整前后两次焊道之间间隔时间实现不同焊接层间温度,以分析焊接速度、焊接层间温度与焊接残余应力之间的规律。
参考表 1数据,对不同焊层焊接工艺参数中的焊接电压和焊接电流进行合理取值,以焊接层间温度和焊接速度为自变量分别选取4组数值,如表 2所示,运用仿真分析Q345钢平板焊接残余应力的分布情况。
| 表 2 焊接层间温度和焊接速度计算数值 Table 2 The calculated values of the welding interpass temperature and welding speed |
分析Q345钢平板构件垂直于焊缝方向的横向焊接残余应力,沿x轴方向测量,不同焊接速度下残余应力分布情况如图 2所示。
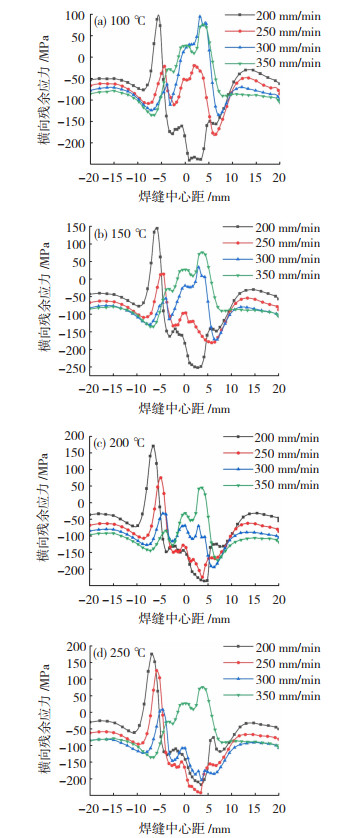
|
图 2 相同焊接层间温度下不同焊接速度的横向残余应力分布规律 Fig.2 The distribution of transverse residual stress at different welding speeds under the same welding interpass temperature |
分析图 2可知,焊接接头的横向残余应力在距离焊缝中心-6~6 mm区间变化大、分布集中,远离焊缝中心处应力逐渐降低,在焊缝中心距-6~-5 mm和4~6 mm的区间主要为不同焊接速度下的焊接残余应力峰值点分布域。横向残余应力均存在拉压两个方向的连续应力变化,仅在焊接层间温度100 ℃、焊接速度250 mm/min和焊接层间温度200 ℃、焊接速度300 mm/min时的横向残余应力为压应力。焊接层间温度在200 ℃及以下时,焊缝横向残余应力的拉压峰值应力波动范围随着焊接层间温度数值增大而急速增大,在250 ℃时横向应力范围的增量放缓。
在相同的焊接层间温度条件下,焊接速度增大时,-6~-5 mm区间的应力峰值减小,4~6 mm区间的应力峰值先减后增,焊接速度在350 mm/min时该区间始终为拉应力峰值点分布域。此外,焊接速度增大,最大横向残余应力值逐渐减小,最小横向残余应力主要为零值,两应力的分布位置均为焊缝区两侧的热影响区。
2.1.2 焊接速度对厚度方向残余应力的影响规律分析Q345钢平板构件的厚度方向焊接残余应力,从平板下底面开始沿y轴方向测量,焊接速度与残余应力分布的关系如图 3所示。
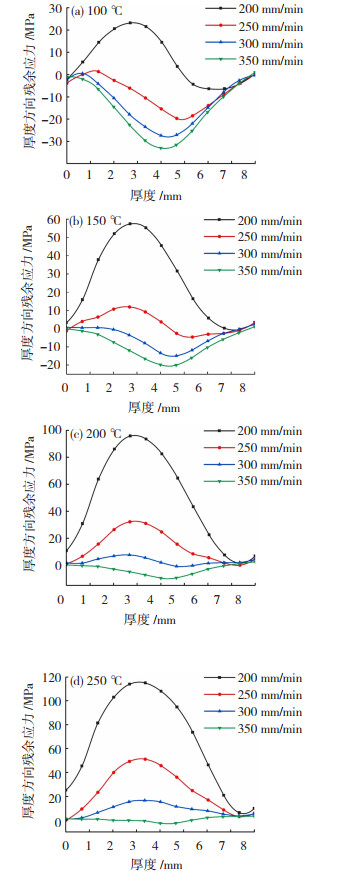
|
图 3 相同焊接层间温度下不同焊接速度的厚度方向残余应力分布规律 Fig.3 The distribution of thickness residual stress at different welding speeds under the same welding interpass temperature |
分析图 3可知,相同条件下厚度方向残余应力的峰值远小于横向残余应力峰值,随着焊接层间温度的增大,厚度方向残余应力的峰值区间逐渐扩大,拉应力的峰值区间大于压应力峰值区间,且在焊接层间温度较大时峰值区间的变化趋于平缓。
随着平板厚度增大,相同焊接层间温度不同焊接速度下残余应力变化梯度均呈现先增后减的变化趋势。焊接速度增加时,厚度方向残余应力逐渐由拉应力变为压应力,其峰值应力位置自平板厚度侧的中间层逐渐向平板上表面偏移。焊接层间温度大于150 ℃、焊接速度200 mm/min时残余应力值最大。
2.2 焊接层间温度影响分析 2.2.1 焊接层间温度对横向残余应力的影响规律不同焊接层间温度下Q345钢平板构件横向残余应力分布情况如图 4所示。
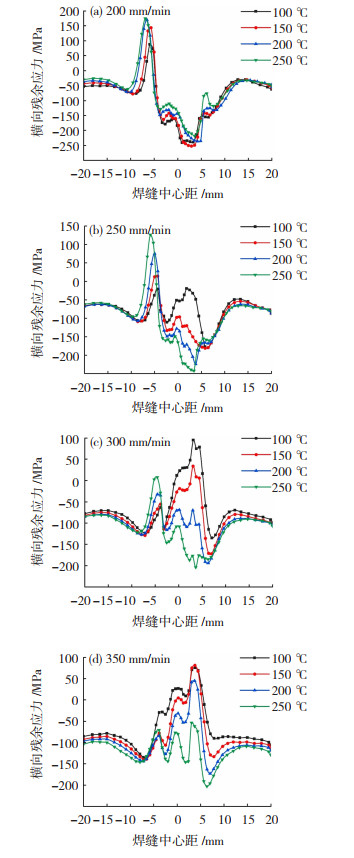
|
图 4 相同焊接速度下不同焊接层间温度的横向残余应力分布规律 Fig.4 The distribution of transverse residual stress at different welding interpass temperatures under the same welding speed |
由图 4可知,焊接速度为200 mm/min时,不同焊接层间温度下横向残余应力分布情况基本一致。焊接速度自250 mm/min增大时,分布均匀的横向残余应力对应的焊接层间温度也逐渐升高。
相同焊接速度,横向残余应力值在熔合区均小于热影响区,焊接速度大于200 mm/min且焊接层间温度增大时,熔合区与热影响区的最大横向残余应力值均逐渐增大,在250 ℃时达到最大值。
2.2.2 焊接层间温度对厚度方向残余应力的影响规律不同焊接层间温度下Q345钢平板构件厚度方向残余应力分布情况如图 5所示。
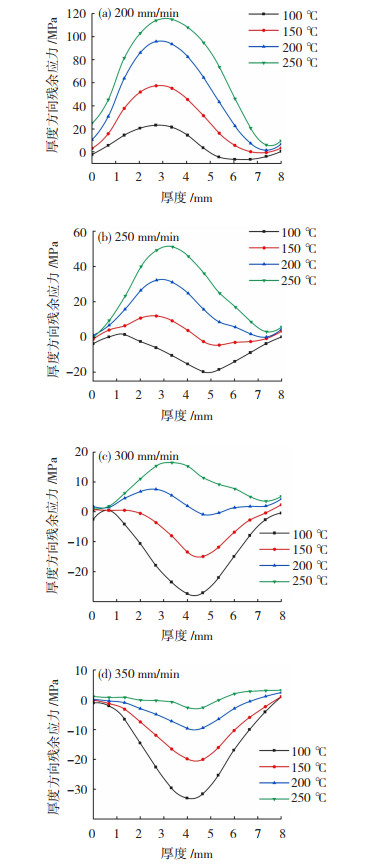
|
图 5 相同焊接速度下不同焊接层间温度的厚度方向残余应力分布规律 Fig.5 The distribution of thickness residual stress at different welding interpass temperatures under the same welding speed |
分析图 5可知,相同焊接速度且小于300 mm/min时,焊接层间温度升高,厚度方向残余应力先减小后增大。焊接速度350 mm/min时,厚度方向残余应力值随层间温度的升高而增大,最大应力值在平板中间层范围。
3 焊接残余应力数学模型与工艺参数优化 3.1 最大焊接残余应力数学模型通过测量残余应力的峰值,分析横向和厚度方向的最大残余应力与焊接速度和焊接层间温度之间的关系,数据如表 3所示。由表 3可以看到,最大横向残余应力值均大于最大厚度方向残余应力值,且随焊接速度加快而减小,随焊接层间温度升高而增大。最大厚度方向残余应力值随焊接速度加快而先减后增,在焊接速度350 mm/min、焊接层间温度250 ℃时最小。
| 表 3 不同焊接层间温度和焊接速度下的最大残余应力值 Table 3 The maximum residual stress values of different welding interpass temperatures and welding speeds |
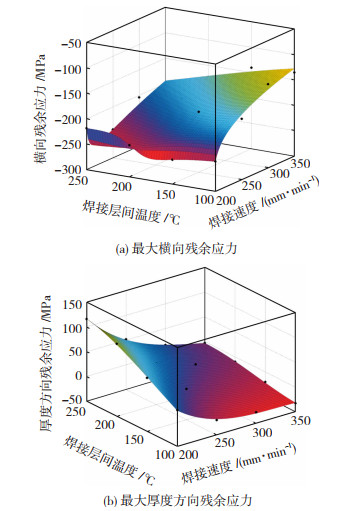
对焊接速度和焊接层间温度两类参数关于横向和厚度方向的最大焊接残余应力进行二元回归分析,拟合模型如图 6所示。
|
图 6 最大横向与厚度方向残余应力的二元回归模型 Fig.6 Binary regression model of maximum transverse and thickness residual stresses: (a) maximum transverse residual stresses; (b) maximum thickness residual stresses |
最大横向残余应力拟合模型的相关系数R值为0.983,最大厚度方向残余应力拟合模型的R值为0.998,拟合模型T与测量数值基本贴合,其数学表达式为
| $ \begin{array}{l} \sigma_{x}=(-269776.7145+3589.8983 v- \\ 10441.3643 T+11.5222 T^{2}+ \\ 29.7901 v T)(1+14.8621 v+23.1446 T- \\ \left.0.122 v^{2}-0.0503 T^{2}-0.0191 v T\right)^{-1} \\ \sigma_{y}=673.3673-7.3014 v+1.5278 T+ \\ 0.0241 v^{2}-0.0083 v T+0.0036 T^{2}- \\ 2.519 \times 10^{-5} v^{3}+5.04 \times 10^{-6} v^{2} T+ \\ 7.512 \times 10^{-6} v T^{2}-1.266 \times 10^{-5} T^{3} \end{array} $ | (4) |
式中:σx为最大横向残余应力,MPa; σy为最大厚度方向残余应力,MPa; T为焊接层间温度,℃。
3.2 数学模型验证为验证式(4)中拟合函数,取焊接速度为250 mm/min,焊接层间温度在100~250 ℃中取若干值,运用仿真计算Q345钢焊接平板在横向和厚度方向的残余应力分布,得到的最大残余应力作为验证模型的仿真值。所取工艺参数值带入式(4)计算,得到的横向与厚度方向的最大残余应力值作为计算值,计算结果与对比误差见表 4。
| 表 4 数学模型仿真值与计算值 Table 4 Simulation values and calculated values of mathematical models |
由表 4可知,横向和厚度方向最大残余应力仿真运算的仿真值与公式计算的计算值偏差较小,数据对比的误差不超过4%,所产生的应力变化基本一致,能够正确反映横向和厚度方向最大残余应力的趋势走向。
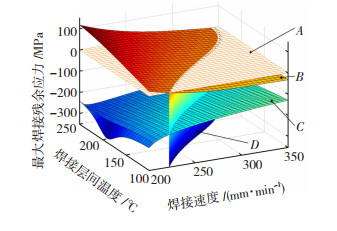
3.3 模型对比与焊接工艺参数优化将最大横向和厚度方向残余应力的拟合模型对比分析,优化焊接工艺参数对焊接残余应力在横向和厚度方向的综合影响,如图 7所示。图 7中:A平面为残余应力为零值的零平面; B、C曲面分别为最大横向和厚度方向残余应力的拟合模型; D曲面为A、B平面交线沿应力坐标轴方向投影的投影面。
|
图 7 焊接最大横向和厚度方向残余应力的拟合模型对比 Fig.7 Comparison of fitting models of maximum transverse and thickness residual stresses |
图 7中,D曲面将B、C两模型分为两部分,沿着焊接速度减小、焊接层间温度升高方向的部分,即D面左侧时,B、C两模型的应力数值均逐渐增大。沿着焊接速度增大、焊接层间温度降低方向的部分,即D面右侧时,B、C两模型的应力数值一增一减, 且均为负值。
由D面右侧和B、C面构成的面域为最大焊接残余应力在横向和厚度方向对焊接接头的综合影响最小的区域,该范围内对焊接速度和焊接层间温度取值,可实现焊接残余应力的优化,为实际焊接作业提供一定指导作用。
4 结论1) Q345钢平板焊接的横向残余应力峰值主要分布在热影响区,焊缝区的应力值较小; 最大厚度方向残余应力分布在平板厚度中心,应力值远小于最大横向残余应力。
2) 焊接速度增大、焊接层间温度降低均使横向残余应力降低,而厚度方向残余应力先减后增; 焊接速度为350 mm/min时,厚度方向残余应力随焊接层间温度升高而增大; 焊接速度和焊接层间温度对横向残余应力的影响大于厚度方向残余应力。
3) 最大横向和厚度方向残余应力拟合模型的梯度关于两焊接工艺参数变化呈相反趋势。依据工艺参数对残余应力的影响程度,可优先考虑减小横向残余应力,即在C、D两曲面交线的基础上向右侧取值,适当增大焊接速度,降低焊接层间温度,减小焊接残余应力对钢构件的影响。
| [1] |
赵阳.高强度结构钢不同焊接接头残余应力分析[D].北京: 华北电力大学, 2018.
|
| [2] |
QIANG B, LI Y, YAO C, et al. Through-thickness welding residual stress and its effect on stress intensity factors for semi-elliptical surface cracks in a butt-welded steel plate[J]. Engineering Fracture Mechanics, 2018, 193: 17-31. DOI:10.1016/j.engfracmech.2018.02.016 |
| [3] |
陈双建.GH3535合金焊接热影响区组织演变及性能研究[D].上海: 中国科学院研究生院(上海应用物理研究所), 2017.
|
| [4] |
RYBICKI E F, STONESIFER R B. Computation of residual stresses due to multipass welds in piping systems[J]. Journal of Pressure Vessel Technology, 1979, 101(2): 149-154. DOI:10.1115/1.3454614 |
| [5] |
钱海盛, 张宇, 邓红川, 等. 焊接工艺参数对Q235钢焊接残余应力的影响[J]. 热加工工艺, 2015(5): 169-171. QIAN Haisheng, ZHANG Yu, DENG Hongchuan, et al. Effect of welding process parameters on welding residual stress of Q235 steel[J]. Hot Working Technology, 2015(5): 169-171. DOI:10.14158/j.cnki.1001-3814.2015.05.052 |
| [6] |
WANG T, LI N, ZHANG Y, et al. Influence of welding speed on microstructures and mechanical properties of vacuum electron beam welded TZM alloy joints[J]. Vacuum, 2018, 149: 29-35. DOI:10.1016/j.vacuum.2017.12.007 |
| [7] |
BALAKRISHNAN J, VASILEIOU A N, FRANCIS J A, et al. Residual stress distributions in arc, laser and electron-beam welds in 30 mm thick SA508 steel: A cross-process comparison[J]. International Journal of Pressure Vessels and Piping, 2018, 162: 59-70. DOI:10.1016/j.ijpvp.2018.03.004 |
| [8] |
蒲晓薇.高强钢厚板结构件焊接接头残余应力与变形的理论预测[D].重庆: 重庆大学, 2017.
|
| [9] |
LIU X M, GAO Y P, WEI Z G, et al. Welding defects of SUPER304H steel and their countermeasures[M]. Singapore: World Scientific, 2016.
|
| [10] |
吕加鹏.铣刨机升降支腿27SiMn合金钢焊接工艺研究[D].长沙: 湖南大学, 2017.
|
| [11] |
王龙.波形腹板H形钢梁的焊接残余应力对性能的影响[D].重庆: 重庆交通大学, 2017.
|
| [12] |
曹现雷, 沈浩, 徐勇, 等. Q800高强钢焊接工字形截面残余应力试验分析[J]. 焊接学报, 2018, 39(3): 36-41. CAO Xianlei, SHEN Hao, XU Yong, et al. Experimental investigation of residual stress in welded Q800 high strength steel I-shaped cross-section[J]. Transactions of the China Welding Institution, 2018, 39(3): 36-41. DOI:10.12073/j.hjxb.2018390064 |
| [13] |
GUANGMING F, JIJUN G, LOURENCO M I, et al. Parameter determination of double-ellipsoidal heat source model and its application in the multi-pass welding process[J]. Ships and Offshore Structures, 2015, 10(2): 204-217. DOI:10.1080/17445302.2014.937059 |
| [14] |
刘晓占.固态相变对P92钢多层多道焊接残余应力影响的研究[D].重庆: 重庆大学, 2015.
|
| [15] |
MENGJIA H, KEJIAN L, ZHIPENG C, et al. A new weld material model used in welding analysis of narrow gap thick-walled welded rotor[J]. Journal of Manufacturing Processes, 2018, 34: 614-624. DOI:10.1016/j.jmapro.2018.06.036 |
| [16] |
ABDELNASSER Y, MA N, RASHED S, et al. Impact strength analysis of plate panels with welding-induced residual stress and deformation[J]. World Journal of Mechanics, 2016, 6(1): 8-17. DOI:10.4236/wjm.2016.61002 |
| [17] |
程家元. 分段焊法在船舶行业大薄板拼接变形控制中的应用[J]. 科学技术创新, 2017(23): 74-75. CHENG Jiayuan. Application of sectional welding method in the control of large thin plate splicing deformation in shipbuilding industry[J]. Scientific and Technological Innovation, 2017(23): 74-75. DOI:10.3969/j.issn.1673-1328.2017.23.046 |
 2020, Vol. 28
2020, Vol. 28


