冲蚀磨损是现代工业生产中常见的一种磨损形式,可以描述为固体表面同含有颗粒的流体接触时表面材料所发生的损耗[1-2],常见于许多工业场合,如锅炉管道外部、石油管道内部和航空航天飞行器表面等[3-5]。冲蚀磨损不仅降低了材料的使用寿命,而且还会导致系统故障。传统的防磨手段主要是开发新型复合材料以及表面的涂层处理技术,这些方法虽然有一定效果,但存在受温度限制严重或者强度性能差等问题[6-9]。因此,寻求一种优异的抗冲蚀磨损新技术已经成为科学研究的热点。
受益于仿生学的启发,学者们针对不同生物进行仿生减磨研究。仿生减磨技术是将某种生物的特殊体表结构应用于材料表面,以增加材料的耐磨性。杨明康[10]以黑粗尾蝎为研究对象,采用显微分析手段分析其体表的不同复合结构,并通过实验表明V型槽结构减磨效果最佳,另外凸包以及六边形凹坑也有一定的减磨效果;戈超[11]以黄肥尾沙漠蝎为研究对象,验证了凹槽结构的优异性,探究了尺寸参数的影响,并将其应用于离心风机叶片。此外,学者们对多种动植物也做了相关研究,孙鸿志[12]、Huang[13]和Han[14]等人分别以贝壳、沙漠蜥蜴和红柳为研究对象,都证明了这些生物体表的结构具有一定的抗冲蚀磨损特性。
学者们多以实验的方法研究仿生结构的减磨特性,颗粒源来自于小直径喷管,且颗粒入射角度比较单一。而在工业的冲蚀磨损场景中,如电厂锅炉受热面和航空航天飞行器大表面,受磨表面暴露在自由冲刷的两相流中,在边界层的影响下,磨损规律与传统的射流实验有所不同。因此,本文重点研究不同颗粒入射角度下仿生表面在大面积两相流下的减磨特性。以沙漠蝎仿生表面为研究对象,提取其凹槽和凸包为仿生结构,确定凹槽、凸包和凹槽+凸包3种仿生表面样本,并以光滑表面作为对照样本。采取CFD数值计算方法对比各工况下的磨损率大小,并从流场和颗粒场两方面详细探讨各仿生结构的减磨特性,以期为仿生结构在工业材料中的进一步应用提供指导。
1 物理模型及数值求解方法 1.1 物理模型沙漠蝎常年受到风沙的冲蚀,通过长期自然选择进化形成特殊的体表形态,在体表结构及其组成材料的协同作用下,表现出优异的抗冲蚀磨损特性。作为仿生减磨最经典的研究对象之一,学者们针对其进行仿生减磨研究时,多是涉及了凸包和凹槽结构,图 1给出了某种典型沙漠蝎的背部表面结构示意图。本文将以这两个结构为基础确定凹槽、凸包和凹槽+凸包3种仿生表面样本,并以光滑表面作为对照样本。

|
图 1 沙漠蝎背部表面结构 Fig.1 Rear structure of the desert scorpion |
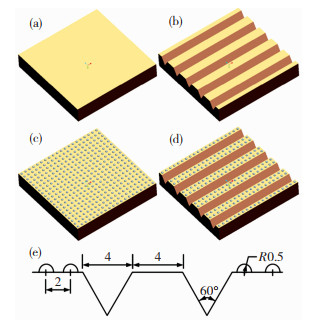
在确定仿生表面结构及尺寸时,考虑到计算的便利性,对形态及尺寸做适当修整。将蝎子背板表面简化为平板,长度和宽度为40 mm,厚度为6 mm。有研究[10, 14]已经验证了V型凹槽的优异减磨特性,因此,确定凹槽结构为V型槽,截面为正三角形,边长和凹槽间距皆为4 mm;凸包为半球状,直径为1 mm,凸包间距为2 mm。图 2给出了4种表面的模型图及其几何模型,其中图 2(a)为光滑表面(A1),图 2(b)为凹槽表面(A2),图 2(c)为凸包表面(A3),图 2(d)为凹槽+凸包表面(A4),图 2(e)为凹槽和凸包结构的几何关系。
|
图 2 4种表面模型及几何模型(单位:mm) Fig.2 Schematic diagrams of four surfaces model |
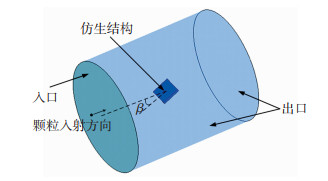
图 3给出了计算流域示意图,为颗粒入射角,即颗粒入射方向与表面的夹角。计算流域为长度300 mm、直径250 mm的管道,为使入口处流场充分发展,将4种表面放置在距离入口150 mm处的截面中心处。其中,凸包和凹槽结构的方向正对气流方向。
|
图 3 计算流域 Fig.3 Calculation basin |
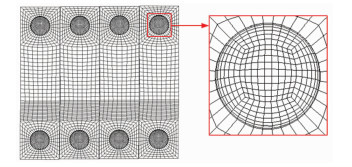
本文采用ICEM对上述4种表面的计算流域进行网格划分。由于结构网格生成速度快且质量更高,因此,采用结构网格进行网格划分。由于3个仿生表面包含微小结构,因此,进行局部网格加密,以充分捕捉仿生表面的流场结构,凹槽+凸包表面的局部网格如图 4所示。
|
图 4 凹槽+凸包表面局部网格 Fig.4 The local grids of bump-groove plate |
为了确定合适的网格数量,以出入口压力波动幅值为指标,进行网格的无关性验证。以光滑表面为例,分别做了50万~250万共5组网格数的模拟,结果如图 5所示,N代表网格数。模拟结果显示,当网格数量大于200万时,指标量的误差为0.8%,计算结果变化幅度在允许的范围内,满足无关性要求。因此,本文网格数确定为200万左右。

|
图 5 网格无关性验证 Fig.5 Independence verification of grids |
颗粒冲蚀表面过程包括流体相运动、颗粒相运动、颗粒碰撞壁面以及磨损等过程,涉及到颗粒碰撞模型和磨损模型。本文选取的表面材料为304不锈钢,颗粒材料选取石英砂,选取的冲蚀模型如下。
1.3.1 颗粒碰撞模型颗粒碰撞包含颗粒-颗粒碰撞和颗粒-壁面碰撞,而文中选用的颗粒浓度相对较低,可忽略颗粒-颗粒碰撞,只考虑颗粒-壁面碰撞。通过fluent自带的UDF功能添加颗粒碰撞模型,文中选用Grant[15-16]给出的通用颗粒碰撞通用模型:
| $ {\frac{{{V_{{{\rm{n}}_2}}}}}{{{V_{{{\rm{n}}_1}}}}} = 1 - 0.4159{\beta _{\rm{p}}} - 0.4994\beta _{\rm{p}}^2 + 0.292\beta _{\rm{p}}^3} $ | (1) |
| $ {\frac{{{V_{{{\rm{t}}_2}}}}}{{{V_{{{\rm{t}}_1}}}}} = 1 - 2.12{\beta _{\rm{p}}} + 3.0775\beta _{\rm{p}}^2 = 1.1\beta _{\rm{p}}^3} $ | (2) |
式中:Vn和Vt分别为颗粒撞击壁面时法向和切向速度,下标1代表颗粒撞击前速度,下标2代表颗粒撞击后速度;βp为颗粒撞击壁面时的碰撞角。
1.3.2 磨损模型在靶材料和颗粒属性确定的情况下,冲蚀磨损率主要取决于颗粒的碰撞速度和碰撞角度。通过Fluent自带的UDF功能添加磨损模型,文中选用Grant和Tabak off[17-18]通过磨损试验结果拟合出的半经验公式如下:
| $ \begin{array}{l} \varepsilon = {K_1}{\left[ {1 + {C_{\rm{k}}}\left( {{K_{12}}\sin \left( {\frac{{90}}{{{\beta _0}}}{\beta _{\rm{p}}}} \right)} \right)} \right]^2}\\ V_{\rm{p}}^2{\cos ^2}{\beta _{\rm{p}}}\left( {1 - R_T^2} \right) + {K_3}{\left( {{V_{\rm{p}}}\sin {\beta _{\rm{p}}}} \right)^4} \end{array} $ | (3) |
| $ {V_{\rm{p}}^2{{\cos }^2}{\beta _{\rm{p}}}\left( {1 - R_T^2} \right) + {K_3}{{\left( {{V_{\rm{p}}}\sin {\beta _{\rm{p}}}} \right)}^4}} $ | (4) |
| $ {{C_{\rm{k}}} = \left\{ {\begin{array}{*{20}{l}} {1, {\beta _{\rm{p}}} \le 2{\beta _0}}\\ {0, {\beta _{\rm{p}}} > 2{\beta _0}} \end{array}} \right.} $ | (5) |
式中:ε为单位质量磨粒引起的重量磨损;β0为产生最大磨损率的碰撞角度;Vp为颗粒碰撞速度;RT为切向恢复比;Ck、K1、K12和K3为系数。
针对颗粒为石英砂,靶材料为不锈钢而言,实验结果拟合得到式(3)中的经验常数取值β0=25°,K1=0.522 5×10-5, K12=0.266 799, K3=0.549×10-12。
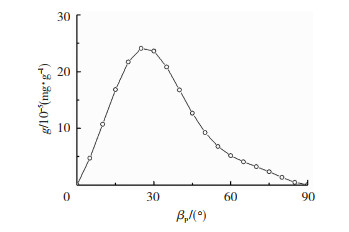
根据上述的冲蚀磨损模型以及石英砂对不锈钢的相关系数,图 6给出了速度为30 m/s时磨损量与碰撞角度的关系。由图 6可以看出,随着碰撞角度增大,磨损量呈现先增大后减小的趋势,在25°附近达到峰值。
|
图 6 磨损量与碰撞角度关系 Fig.6 Relationship between erosion rate and impact angle |
网格面的磨损率定义为单位面积上所有与之碰撞的颗粒产生的冲蚀量的累加,
| $ {E_0} = \sum\limits_{p = 1}^N {\frac{{{m_{\rm{p}}}{\varepsilon _{\rm{p}}}}}{{{A_{{\rm{face}}}}}}} $ | (6) |
式中:E0为网格面的磨损率;N为与网格面发生碰撞的颗粒数;mp为颗粒的质量流量;εp为利用式(3)计算的某一颗粒对网格面的磨损率;Aface为网格面的面积。
1.4 边界条件采用速度入口边界条件,空气入口速度为30 m/s,湍流参数采用水力直径和湍流强度定义。出口采用压力出口边界条件。颗粒入射源均匀分布在整个入射面,颗粒总数78万左右,颗粒入射速度和流体速度一致。入射颗粒粒径为50 μm,密度为2 650 kg/m3,颗粒质量流量为0.025 kg/s。湍流模型采用标准k-ε模型,近壁区采用标准壁面函数法,壁面采用无滑移边界条件。速度-压力耦合采用SIMPLEC算法,收敛标准为所有监测变量的残差小于10-5。
1.5 数值计算流程本文首先确定这4种几何模型的构造及尺寸,并分别构建各样本在颗粒入射角为15°、30°、45°、60°和90°下的几何模型,共计20个模型。再进行各模型的网格划分,最后设置相关模型和边界条件。在数值计算时,先进行流场计算,待流场计算稳定后,导入颗粒场进行耦合计算,待颗粒场计算稳定后结束整个计算过程。其中壁面设置为反射边界条件,采用式(1)和式(2)的反弹模型,磨损率计算模型采用式(3)中石英砂对不锈钢的磨损率计算模型。
2 模型验证为验证数值模拟的准确性,本文针对文献[10]所做的颗粒入射角为30°的仿生表面磨损实验结果进行数值模拟对比。选取其中的光滑表面、凹槽表面和凹槽+凸包表面在小粒径石英砂颗粒冲撞的工况下进行对比,构建相同几何模型及贴近实验条件的计算流域,选取一致的颗粒以及靶材料特性参数,设置上述的边界条件、颗粒碰撞模型和颗粒反弹模型。
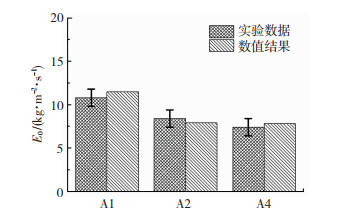
图 7给出了冲蚀磨损实验与数值模拟的结果对比,结果表明,数值模拟的计算结果与该实验数据存在小部分误差,这主要是由于实验的某些条件与数值模拟时无法完全一致所致,且数值模拟采取平均粒径代替其实际的粒径分布情况。但误差在允许范围,且不同结构磨损率的相对比例较为一致,这表明本文使用的边界条件以及相关模型是适用的。
|
图 7 磨损实验与数值模拟的结果对比 Fig.7 Comparison between results of experiment and simulation |
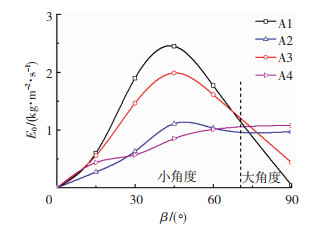
图 8给出了4种表面随颗粒入射角变化的磨损率曲线。从图 8可以看出,光滑表面和凸包表面的磨损率曲线呈“拱形”,即磨损率随颗粒入射角的增加先增大后减小。其曲线趋势与图 6的一致,但达到磨损率峰值的角度从25°附近变成45°附近,主要是因为改变颗粒入射角度时碰撞的颗粒数也改变,且边界层对颗粒场的影响不同,在3.3节将进一步阐述这一现象。凹槽表面和凹槽+凸包表面的磨损率随颗粒入射角的增加先增大后趋于平缓,相对于光滑表面而言,整体磨损率较小,但在颗粒入射角为90°时磨损率较大。在颗粒入射角小于70°时,3种仿生表面的磨损率均低于光滑表面,因此以70°作为大小角度的分界线。
|
图 8 4种表面磨损率曲线 Fig.8 Erosion rate curve of the four plates |
当颗粒入射角为小角度时,3种仿生表面均表现出一定的减磨效果,其中凹槽表面和凹槽+凸包表面效果更佳,即凹槽结构表现出较好的减磨效果。当入射角为大角度时,3种仿生表面的磨损率均大于光滑表面,带有凹槽结构的表面磨损率较大。对比各仿生表面的相对磨损率可知,凹槽+凸包表面仿生表面在颗粒入射角为45°时减磨效果最好,相比于光滑表面,磨损率降低65.3%左右。
当颗粒入射角为小角度时,相较于光滑表面,3种仿生表面的磨损率都有所减小,在颗粒入射角为45°时减磨效果尤为显著。图 9给出了颗粒入射角为45°时4种表面的局部磨损率云图。

|
图 9 45°入射角4种表面的磨损率云图:(a)A1;(b)A2;(c)A3;(d)A4 Fig.9 Contour plot of the erosion rate at 45°: (a)A1;(b)A2;(c)A3;(d)A4 |
由图 9(a)可以看出,光滑表面磨损率分布比较均匀,整体磨损率较大。由图 9(b)可以看出,相较于光滑表面,凹槽表面槽内磨损率大幅度减小,但凹槽表面两侧磨损率略有增大,区域1的磨损率增大了5%。由图 9(c)可以看出,凸包表面各凸包结构正面磨损率分布不均且小部分位置磨损率较大,但由于正面的遮挡作用,磨损率大幅度减小,即背面形成了遮蔽区域,整体磨损率略微减小。由上述分析可知,凹槽表面减磨效果好,针对凹槽两侧的平面磨损率略有增大的问题,凸包结构又能起到一定的减磨效果,在凹槽表面两侧加入凸包结构后,图 9(d)区域2磨损率比图 9(b)区域1减小了21%。因此,凹槽+凸包表面结合了两种仿生结构的优点,整体磨损率最小。
当颗粒入射角为大角度时,相较于光滑表面,3种仿生表面的磨损率都增大。磨损率增大的原因主要是仿生结构将颗粒撞击角度从90°改变到磨损率更大的小角度。针对凹槽结构,由于截面为正三角形的结构,因此,颗粒碰撞角度几乎都在磨损率最大的30°左右。针对凸包结构,颗粒碰撞角则从中心的90°向四周逐渐变化到接近0°。
仿生结构改变了表面的边界层,使流场发生改变,进而改变了颗粒场的相关参数,最终影响磨损率的分布情况及数值大小。本文进一步从流场和颗粒场两方面对仿生表面的减磨机理进行了研究。
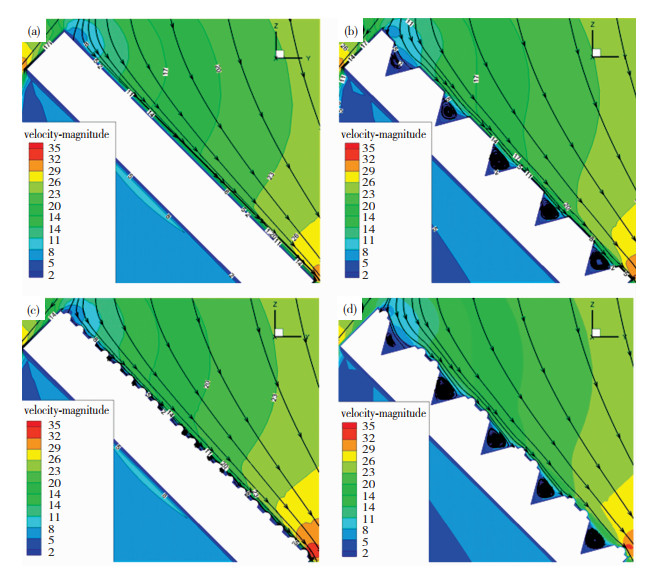
3.2 流场分析为进一步解释磨损率分布规律,先研究仿生结构对边界层流场的具体影响,以颗粒入射角45°为例,图 10给出了中间截面上4种表面的速度场和流线图。对比速度场云图可以看出,光滑表面的流体速度大于凸包和凹槽结构附近。对于凸包结构,表面流体速度略有减小,凸包间流体的速度减小程度大于凸包表面;对于凹槽结构,槽内流场速度明显小于其他结构附近,因此,凹槽对速度流场的影响最大。对比流线图可以看出,光滑表面流体顺利流过表面;凸包间流线出现弯曲,且部分凸包附近出现涡结构,但涡结构尺度较小,即凸包对流体起到一定的扰动作用;而所有凹槽结构内流体均旋转流动,出现了尺度较大的涡结构,因此对流体起到了较大的扰动作用。
|
图 10 4种表面中间截面速度场和流线图:(a)A1;(b)A2;(c)A3;(d)A4 Fig.10 Velocity field and streamline diagram of the four surfaces: (a)A1;(b)A2;(c)A3;(d)A4 |
结合速度场云图和流线图可知,凸包结构对流场的影响有限,除了使流线略微的弯曲之外,部分区域产生的小尺度涡结构也一定程度影响流体的速度;凹槽结构则每个模块内部均形成较为稳定的大尺度涡结构,湍流强度较高,流体速度较低。
3.3 颗粒场分析图 11和图 12分别给出了不同颗粒入射角度下各表面的平均碰撞角度和平均碰撞速度。由图 11可以看出,与颗粒入射角相比,光滑表面的颗粒碰撞角度略有减小,且变化幅度很小。针对仿生表面而言,在颗粒入射角较小时,各仿生表面整体的碰撞角度变化很小,其值略有降低;在颗粒入射角较大时,各仿生表面整体的碰撞角度变化幅度增大,特别是在颗粒入射角为90°时,各仿生表面碰撞角度下降约30%,这也解释了仿生表面在颗粒入射角为大角度时磨损率反而增加的原因。相较于光滑表面,凸包表面整体的碰撞角度改变幅度最大。

|
图 11 不同模型下的颗粒平均碰撞角度 Fig.11 The average impact angle of every model |
|
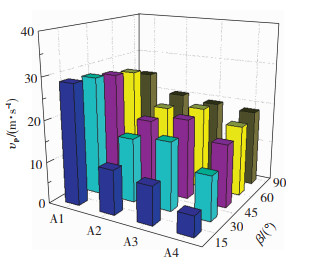
图 12 不同模型下的颗粒平均碰撞速度 Fig.12 The average impact velocity of every model |
由图 12可以看出,与颗粒原始入射速度30 m/s相比,光滑表面的颗粒碰撞速度略有减小,且减小幅度随颗粒入射角增大而增大。针对仿生表面,颗粒碰撞速度均有较大幅度降低,减小幅度随颗粒入射角增大而减小,即在小角度下仿生表面的边界层对颗粒碰撞速度影响更大,减磨效果更好。相较于光滑表面,凹槽+凸包表面整体的碰撞速度下降幅度最大。
关于磨损率随颗粒入射角度的变化曲线峰值与理论不一致的问题,主要有两方面的原因。一方面是当颗粒入射角度改变时,各表面在颗粒入射方向的投影面积发生改变,颗粒入射角度越大,撞击的颗粒数量也越大。另一方面是颗粒碰撞的角度和速度发生变化,对比颗粒入射角为30°和45°的情况可知,两者颗粒碰撞角度均在理论磨损率较大的35°左右,而后者的颗粒碰撞速度是前者的1.4倍。总之,颗粒入射角为45°时颗粒碰撞数量更多,碰撞速度更大,而碰撞角度也处于磨损率较大的位置,因此,磨损率更大。
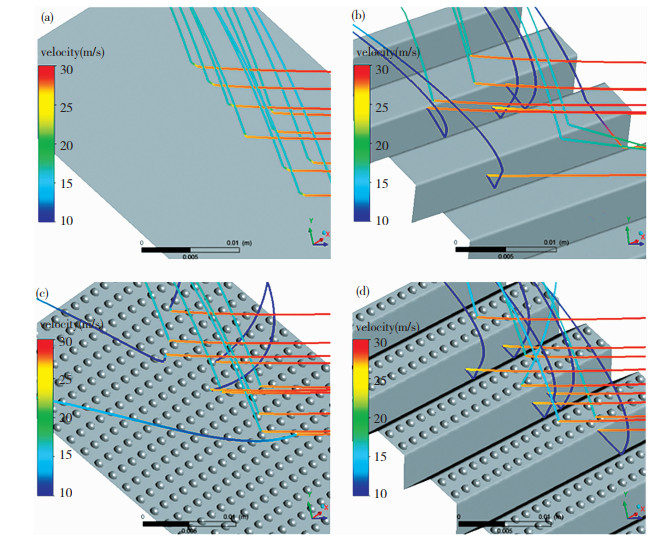
接下来以45°颗粒入射角为例,具体分析颗粒的碰撞轨迹,图 13给出了该角度下4种表面的局部颗粒碰撞轨迹图。由颗粒轨迹的速度线可以看出,颗粒在碰撞4种表面前,颗粒速度在边界层附近迅速降低。由图 13(a)可以看出,当颗粒与光滑表面碰撞时,颗粒反弹角度均一致,且颗粒撞击后速度也相同。由图 13(b)可以看出当颗粒与凹槽结构碰撞时,进入槽内的颗粒速度有较为明显的降低,碰撞后均发生二次碰撞且碰撞后颗粒速度较低,部分颗粒在进入凹槽时动能已被大部分消耗,有的在涡结构的作用下甚至未与表面碰撞便直接离开表面。由图 13(c)可以看出,当颗粒与凸包结构碰撞时,由于曲面形状不规则,颗粒的反射方向和角度都各不相同,存在一些二次碰撞,碰撞后的速度也明显低于光滑表面。由图 13(d)可以看出,凹槽+凸包表面上的颗粒碰撞轨迹包含了图 13(b)和图 13(c)中存在的各种情况。
|
图 13 4种表面局部颗粒碰撞轨迹图:(a)A1;(b)A2;(c)A3;(d)A4 Fig.13 Plot of particles impact track of the four surfaces: (a)A1;(b)A2;(c)A3;(d)A4 |
结合上述可知,颗粒碰撞角度和碰撞速度的改变是减磨的主要因素,虽然仿生结构存在颗粒多次碰撞的现象,但颗粒在第一次碰撞后动能已基本被消耗完毕,后续碰撞造成的磨损率可忽略。值得注意的是,颗粒多次碰撞虽然不影响整体磨损大小,但一定程度降低了图 12中的仿生结构的颗粒碰撞平均速度,即仿生结构首次颗粒碰撞速度应略大于图中的数值,但具体数值难以捕获。
4 结论1) 颗粒入射角小于70°时,各仿生表面均有减磨效果。凹槽结构的减磨效果优于凸包结构,凹槽+凸包表面结合两种结构的优点,在入射角为45°时达到最佳减磨效果,磨损率降低65.3%。
2) 部分凸包结构间形成小尺度涡结构,而每个凹槽结构内均形成稳定的大尺度涡结构。涡结构影响了流体方向并降低了流体速度,进而改变了颗粒场相关参数。
3) 各仿生表面的碰撞角度均降低,其中凸包表面的改变幅度最大。各仿生表面的碰撞速度均明显降低,降低幅度随颗粒入射角度的增大而减小,其中凹槽+凸包表面的下降幅度最大。
4) 对比颗粒入射角为30°和45°的颗粒碰撞角度和颗粒碰撞速度,二者碰撞角度均在35°左右,而后者的碰撞速度是前者的1.4倍。
| [1] |
赵宪萍, 叶桂林, 朱崇武, 等. 不同温度工况下飞灰磨损速度指数特性的试验研究[J]. 上海电力学院学报, 2016, 32(1): 1-4. ZHAO Xianping, YE Guilin, ZHU Chongwu, et al. Experimental study on the characteristic of velocity index for flying-ash erosion at different temperature conditions[J]. Journal of Shanghai University of Electric Power, 2016, 32(1): 1-4. DOI:10.3969/j.issn.1006-4729.2016.01.001 |
| [2] |
BOUSSER E, MARTINU L, KLEMBERG S J E. Solid particle erosion mechanisms of protective coatings for aerospace applications[J]. Surface & Coatings Technology, 2014, 257: 165-181. DOI:10.1016/j.surfcoat.2014.08.037 |
| [3] |
KANG Rong, LIU Haixiao. A unified explicit correlation of predicting the sand erosion in elbows for gas and annular flows based on probability analysis[J]. Wear, 2019, 428-429: 279-292. DOI:10.1016/j.wear.2019.03.023 |
| [4] |
LI Mingjia, TANG Songzhen, WANG Feilong, et al. Gas-side fouling, erosion and corrosion of heat exchangers for middle/low temperature waste heat utilization: A review on simulation and experiment[J]. Applied Thermal Engineering, 2017, 126: 737-761. DOI:10.1016/j.applthermaleng.2017.07.095 |
| [5] |
SZYMAÑSKI K, HERNAS A, MOSKAL G, et al. Thermally sprayed coatings resistant to erosion and corrosion for power plant boilers-A review[J]. Surface & Coatings Technology, 2015, 268: 153-164. DOI:10.1016/j.surfcoat.2014.10.046 |
| [6] |
斯松华, 姜闪闪, 王妍妍. Ti对等离子堆焊Ni基Cr3C2涂层组织与性能的影响[J]. 材料科学与工艺, 2019, 27(3): 66-70. SI Songhua, JIANG Shanshan, WANG Yanyan. Effect of Ti on microstructure and properties of Ni-base Cr3C2 coating prepared by a plasma surfacing[J]. Materials Science and Technology, 2019, 27(3): 66-70. DOI:10.11951/j.issn.1005-0299.20170253 |
| [7] |
代礼葵, 孙耀宁, 王国建. 紫外辐照对玻纤增强树脂基复合材料冲蚀性能的影响[J]. 材料科学与工艺, 2019, 277(5): 52-58. DAI Likui, SUN Yaoning, WANG Jianguo. Effects of UV irradiation on the erosion performance of glass fiber reinforced resin-based composites[J]. Materials Science and Technology, 2019, 277(5): 52-58. DOI:10.11951/j.issn.1005-0299.20180162 |
| [8] |
EVANS A G, GULDEN M E, ROSENBLATT M. Impact damage in brittle materials in the elastic-plastic response regime[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1978, 361(1706): 343-365. DOI:10.1098/rspa.1978.0106 |
| [9] |
HUTCHINGS I M. A model for the erosion of metals by spherical particles at normal incidence[J]. Wear, 1981, 70(3): 269-281. DOI:10.1016/0043-1648(81)90347-1 |
| [10] |
杨明康. 不同生境下蝎子体表抗冲蚀特性的比较仿生研究[D]. 长春: 吉林大学, 2017. YANG Mingkang. Comparative bionic research on erosion resistance of scorpions cuticle in different habitates[D]. Changchun: Jilin University, 2017. |
| [11] |
戈超. 离心风机叶片抗冲蚀磨损仿生研究[D]. 长春: 吉林大学, 2011. GE Chao. Bionic investigation on erosion resistance of centrifugal fan blades[D]. Changchun: Jilin University, 2011. |
| [12] |
孙鸿志. 管道弯头仿生表面耐冲蚀磨损性能及机理研究[D]. 长春: 吉林大学, 2017. SUN Hongzhi. Research on anti-erosion performance and mechanism of a pipe bend with the bio-inspired internal surface[D]. Changchun: Jilin University, 2017. |
| [13] |
HUANG He, ZHANG Yan, REN Luquan. Particle erosion resistance of bionic samples inspired from skin structure of desert lizard, laudakin stoliczkana[J]. Journal of Bionic Engineering, 2012, 9(4): 465-469. DOI:10.1016/S1672-6529(11)60141-8 |
| [14] |
HAN Z W, YIN W, ZHANG J Q, et al. Erosion-resistant surfaces inspired by Tamarisk[J]. Journal of Bionic Engineering, 2013, 10(4): 479-487. DOI:10.1016/S1672-6529(13)60238-3 |
| [15] |
WANG Z L, FAN J R, LUO K. Numerical study of solid particle erosion on the tubes near the side walls in a duct with flow past an aligned tube bank[J]. AIChE Journal, 2010, 56(1): 66-78. DOI:10.1002/aic.11971 |
| [16] |
FAN J R, YAO J, ZHANG X Y, et al. Experimental and numerical investigation of a new method for protecting bends from erosion in gas-particle flows[J]. Wear, 2001, 251(1-12): 853-860. DOI:10.1016/S0043-1648(01)00742-6 |
| [17] |
YAO J, ZHANG B Z, FAN J R. An experimental investigation of a new method for protecting bends from erosion in gas-particle flows[J]. Wear, 2000, 240(1-2): 215-222. DOI:10.1016/S0043-1648(00)00359-8 |
| [18] |
GRANT G, TABAKOFF W. Erosion prediction in turbomachinery resulting from environmental solid particles[J]. Journal of Aircraft, 1975, 12: 471-479. DOI:10.2514/3.598 |
 2021, Vol. 29
2021, Vol. 29


