微束等离子弧焊是一种小电流焊接工艺,适用于汽车制造、航空航天等领域的薄壁件电弧修复及增材制造[1]。由于薄壁特征及制造过程中的往复热累积,堆焊层将出现向两侧“下塌”的现象,导致成形精度降低、综合性能变差。本文提出采用外加横向稳态磁场辅助焊接过程的方法,利用非接触电磁力调控电弧对熔池的热、力输入,达到改善堆焊层形貌与提高堆焊层性能的目的。
由于电弧反应过程极为复杂,难以对外加磁场后电弧特性及电弧对工件的热输入和力输入进行直接测量,因此,通常借助数值模拟的方法进行分析。目前,已有利用数值模拟方法对焊接电弧进行研究的报道[2-3]。陈树君等[4]建立了变极性等离子电弧的三维模型,对EN、EP两种情况下的温度场、电弧压力、电流密度分布特征进行了分析。刘政军等[5]建立了GTAW电弧二维轴对称模型,得到纵向磁场作用下电弧形态、温度、流速、电流、阳极热流密度等变化情况。周祥曼等[6-7]建立了基于GMAW电弧和熔池的弱耦合数值模型,分析了有无外加横向磁场作用下熔池电磁力分布、电弧和熔池传热传质的差异。但国内外对微束等离子电弧研究较少,特别是外加磁场对微束等离子特性影响的研究。
本文依据微束等离子焊枪尺寸建立电弧物理模型,考虑到压缩喷嘴对电弧的约束与钨针尖端损耗,使用COMSOL软件进行电-磁-热-流四场耦合计算,得到了有无外加磁场作用下微束等离子电弧的特性,利用CCD拍摄电弧轮廓对仿真结果进行验证,并在薄壁件上进行多层堆焊试验,以期为薄壁件的磁场辅助电弧增材制造技术提供一定的理论依据。
1 模型建立 1.1 模型假设为了简化模型且得到合理的计算结果,做出如下假设:
1) 电弧等离子体满足局部热力学平衡状态;
2) 电弧等离子体是连续的,层流的,忽略重力;
3) 等离子气为纯氩气,其电导率、热导率仅为温度的函数;
4) 电弧中无位移电流;
5) 外加磁场为均匀的稳态磁场。
1.2 控制方程组基于以上假设,控制方程组如下。
质量守恒方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho \nu ) = 0 $ | (1) |
动量守恒方程:
| $ \begin{array}{*{20}{c}} {\rho \left( {\frac{{\partial \nu }}{{\partial t}} + \nu \cdot \nabla \nu } \right) = \nabla \cdot [ - p\mathit{\boldsymbol{I}} + }\\ {\left. {\mu \left( {\nabla \nu + {{(\nabla \nu )}^T}} \right) - \frac{2}{3}\mu (\nabla \cdot \nu )\mathit{\boldsymbol{I}}} \right] + {S_\Phi }} \end{array} $ | (2) |
式(1)、(2)是对流场进行描述。
能量守恒方程:
| $ \rho {C_p}\left( {\frac{{\partial T}}{{\partial t}} + v \cdot \nabla T} \right) = \nabla \cdot (k\nabla T) + S $ | (3) |
式中:ρ为密度;υ为速度矢量;p为压力;μ为粘度;T为温度;Cp为比热容;k为热传导系数。
式(3)是对流体传热进行描述。
SФ为动量守恒方程源项,并施加y方向磁场,表达式为
| $ {S_\Phi } = \mathit{\boldsymbol{J}} \times \mathit{\boldsymbol{B}} = \left\{ {\begin{array}{*{20}{l}} {{B_z} \times {J_y} - \left( {{B_y} + {B_{ - y}}} \right) \times {J_z}}\\ {{B_x} \times {J_z} - {B_z} \times {J_x}}\\ {\left( {{B_y} + {B_{ - y}} \times {J_x} - {B_x} \times {J_y}} \right)} \end{array}} \right. $ | (4) |
式中:Bx、By、Bz为电弧自身磁场,By为外加磁场,文中取30 mT。
S为能量守恒方程源项,表达式为
| $ S = \mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{E}} + \frac{{5{k_{\rm{B}}}}}{{2e}}j \cdot \nabla T - {Q_{{\rm{rad}}}} $ | (5) |
式中:为J·E焦耳加热项;
为计算上述电磁力与焦耳热,需要计算出电流密度J与磁通量B,用电流连续性方程与安培定律计算电势V与磁失势A。
| $ {\nabla \cdot \left( {\sigma \nabla V - \sigma \frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial t}}} \right) = 0} $ | (6) |
| $ {\sigma \frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial t}} + \nabla \times \left( {\frac{1}{{{u_0}}}\nabla \times \mathit{\boldsymbol{A}}} \right) + \sigma \nabla V = 0} $ | (7) |
式(6)、(7)是对电磁场进行描述。
根据V与A计算电流密度、电场与磁通量为
| $ {\mathit{\boldsymbol{J}} = - \sigma \nabla V - \sigma \frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial t}}} $ | (8) |
| $ {\mathit{\boldsymbol{E}} = - \nabla V - \frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial t}}} $ | (9) |
| $ {\mathit{\boldsymbol{B}} = \nabla \times \mathit{\boldsymbol{A}}} $ | (10) |
建立微束等离子弧焊电弧三维模型如图 1所示,该模型包括钨针、压缩喷嘴、空气域、电弧计算域及工件。其中钨针直径1.0 mm,考虑钨针在高温下耗损,将钨针简化为直径0.1 mm且带有60°倾角的尖端,喷嘴口径1.0 mm,钨针内缩2 mm,喷嘴距工件3 mm,焊接电流14 A,等离子气流量0.3 L/min,保护气流量10 L/min。其中,A为钨针侧面;B为等离子气气入口;C为钨针上端面;D为保护气入口;E为电弧计算域;F为保护气出口;G为焊件上表面;H为焊件侧面;I为压缩喷嘴内壁,边界条件见表 1。

|
图 1 电弧物理模型 Fig.1 Physical model of arc |
| 表 1 边界条件 Table 1 Boundary conditions |
保护气速度与气流量大小、保护气喷嘴内径、压缩喷嘴尺寸等相关,计算公式如下[8-9]。
| $ v(r) = \frac{{2Q}}{{\rm{ \mathsf{ π} }}}\frac{{\left\{ {R_{\rm{n}}^2 - {r^2} + \left( {R_{\rm{n}}^2 - R_{\rm{w}}^2} \right)\frac{{\ln \left( {r/{R_{\rm{n}}}} \right)}}{{\ln \left( {r/{R_{\rm{w}}}} \right)}}} \right\}}}{{\left\{ {R_{\rm{n}}^4 - R_{\rm{w}}^4 + \frac{{\left( {R_{\rm{n}}^4 - R_{\rm{w}}^4} \right)}}{{\ln \left( {{R_{\rm{n}}}/{R_{\rm{w}}}} \right)}}} \right\}}} $ | (11) |
式中:Q为保护气流量;Rn为保护气喷嘴内径;Rw为压缩喷嘴尺寸。
等离子气速度与气流量大小、压缩喷嘴内径相关,计算公式为
| $ v\left( {{r_1}} \right) = \frac{{{Q_1}}}{{{\rm{ \mathsf{ π} }}{r^2}}}, r = \sqrt {{x^2} + {y^2}} $ | (12) |
式中: Q1为等离子气流量.
在阴极和阳极表面,即电极鞘层上有几个平均自由程长度的边界层,这些边界层不处于局部热力学平衡状态,却对电弧与熔池的传热传质有着重要的影响,因此,需要对其能量通量进行计算[10-11]。
阴极:
| $ - \mathit{\boldsymbol{n}} \cdot ( - k\nabla T) = \left| {{\mathit{\boldsymbol{J}}_{\rm{i}}}} \right|{V_{\rm{i}}} - \left| {{\mathit{\boldsymbol{J}}_{\rm{e}}}} \right|{\phi _{\rm{c}}} - \varepsilon {\sigma _{\rm{B}}}{T^4} $ | (13) |
阳极:
| $ - \mathit{\boldsymbol{n}} \cdot ( - k\nabla T) = \left| {\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{n}}} \right.{\phi _{\rm{a}}} - \varepsilon {\sigma _{\rm{B}}}{T^4} $ | (14) |
式中:|Ji|Vi代表氩电离产生离子加热,|Je|φc代表电子发射消耗能量;εσBT4代表辐射损失能量;|J·n|φa代表从电子转移到阳极的能量;Ji为离子电流;Je为电子电流;Vi为氩气电离电位;φc为阴极功函数;φa为阳极功函数。
Ji与Je计算如下:
| $ {{\mathit{\boldsymbol{J}}_{\rm{e}}} = {\mathit{\boldsymbol{J}}_{\rm{r}}}\left[ {\left( {|\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{n}}| - {\mathit{\boldsymbol{J}}_{\rm{r}}}} \right) > 0} \right] + // |\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{n}}|\left[ {\left( {|\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{n}}| - {\mathit{\boldsymbol{J}}_{\rm{r}}}} \right) < 0} \right]} $ | (15) |
| $ {{\mathit{\boldsymbol{J}}_{\rm{i}}} = |\mathit{\boldsymbol{J}} \cdot \mathit{\boldsymbol{n}}| - {\mathit{\boldsymbol{J}}_{\rm{e}}}} $ | (16) |
| $ {{\mathit{\boldsymbol{J}}_{\rm{r}}} = {A_{\rm{r}}}{T^2}\exp \left( {\frac{{ - e{\phi _{\rm{e}}}}}{{{k_{\rm{B}}}T}}} \right)} $ | (17) |
式中:Ar为理查森常数;Je热离子发射的有效功函数;e为电荷量.
工件与空气接触的部分为对流边界条件,其热通量表示为
| $ - {q_0} = h\left( {{T_{{\rm{ext}}}} - T} \right) $ | (18) |
式中:h为对流换热系数;Text为外部温度。
保护气与等离子气均使用纯氩气,工件使用AISI304不锈钢,其热物理参数见参考文献[10, 12]。以COMSOL中物理场控制网格进行细化网格划分,共划分207 842个四面体单元,其中包括13 718个边界元和1 152个边单元,最小单元0.024 71,求解的自由度数为716 884,为缩短计算时间,提高计算精度,模型采用以上一次计算得到的解为初始值进行参数化扫描计算。
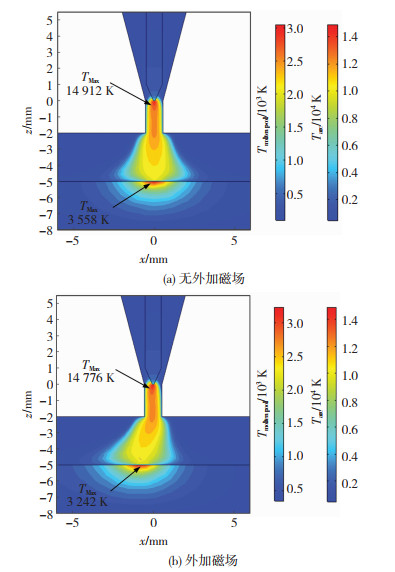
2 仿真结果分析 2.1 温度场计算结果与分析图 2为有/无外加稳态磁场作用下电弧与熔池温度场计算结果。无外加磁场时,由于喷嘴的机械压缩作用,喷嘴内部电弧温度较高且分布集中[13],温度梯度较小,最高温度为14 912 K。在喷嘴下方,由于未受到喷嘴限制,且处于自身产生的磁场中,电弧温度分布较分散,整体形状以电极轴线为中心呈“钟罩”形分布。熔池位于焊件中心位置,最高温度为3 558 K;当施加横向磁场后,电弧等离子体不只是处于自身产生环形对称的洛伦兹力中,在外加电磁力作用下,由于喷嘴的限制作用,喷嘴内部未发生明显变化,最高温度为14 776 K。喷嘴下方的电弧等离子体向x负方向移动,导致电弧形态向x负方向发生偏转。熔池随电弧偏转而向x负方向移动,最高温度降低为3 242 K。
|
图 2 电弧与熔池温度场分布 Fig.2 Temperature field distribution of arc and molten pool: (a) without external magnetic field; (b) with external magnetic field |
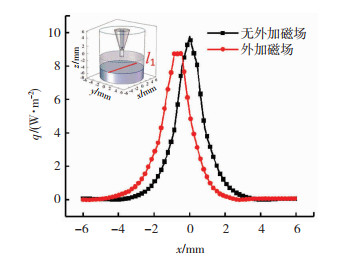
图 3为工件上表面截线l1上的热通量分布曲线,可见,无外加磁场时,工件上表面热通量符合高斯分布特征,在工件中心位置达到最大值9.76×106 W/m2;外加磁场后,最大热通量位置远离工件中心,位于x负半轴,在x=-0.857 mm处取得最大值8.74×106 W/m2,热通量最大值减小,降幅约为10.5%。这是由于电弧偏转增加了电弧长度,电弧与外界接触面积增大,电弧散热增加,导致电弧最大热通量减小,电弧对熔池热输入降低。
|
图 3 l1上热通量分布曲线 Fig.3 Heat flux distribution curve on l1 |
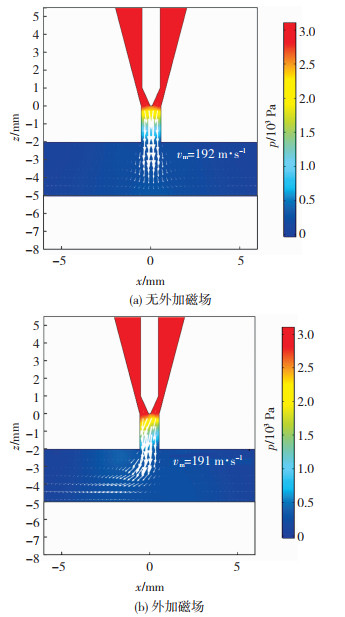
图 4为电弧流场计算结果,其中云图代表压力分布,箭头描述电弧等离子体流动。无外加磁场时,电弧等离子体流速在喷嘴内部较大,约为192 m/s,压力在钨针附近较大,最大约为3 120 Pa,从钨针至工件逐渐减小,从云图中可见,在钨针下端压力云图有明显的平行分层;当施加横向磁场后,由于等离子体流速与压力最大值都位于喷嘴内部,因此最大值无明显变化,但在钨针下端压力分布出现明显变化,在喷嘴内部的同一水平线上,x负半轴侧压力大于正半轴侧压力。
|
图 4 电弧流场分布 Fig.4 Flow field distribution of arc: (a) without external magnetic field; (b) with external magnetic field |
外加磁场对电弧等离子体流动方向影响较大,无外加磁场时直接向下,到达工件上表面后再均匀的向四周流动;外加磁场后,电弧等离子体流动方向改变为离开喷嘴后直接向x负方向流动。这是由于在外加磁场作用下,电弧等离子体受到向x负方向的洛伦兹力,使得电弧等离子体向x负方向移动,最终造成压力与流动方向发生改变。
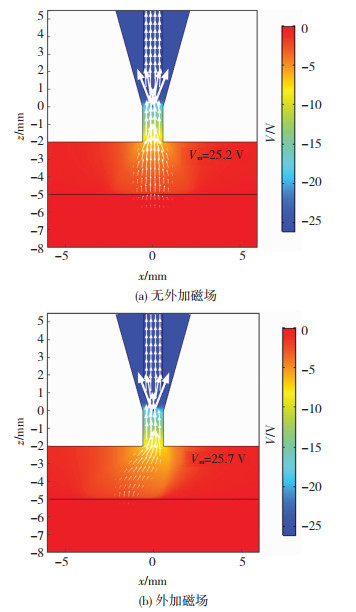
2.3 电场计算结果与分析图 5为电弧电场计算结果,其中云图代表电势分布,箭头描述电流密度。无外加磁场时,电流由工件流出,经电弧计算域流至钨针,在钨针下端面取得最大值4.52×108 A/m2;外加磁场后,钨针尖端电流密度最大值减小,但减小幅度较小,约为4.37×108 A/m2,这是由于钨针下端面面积较小,导致电流密度在此处较大。电势分布与温度场类似,但外加磁场后,由于电弧长度增加,电弧计算域内电压变大,由无外加磁场时的25.2 V增加至25.7 V。
|
图 5 电弧电场分布 Fig.5 Electric field distribution of arc: (a) without external magnetic field; (b) with external magnetic field |
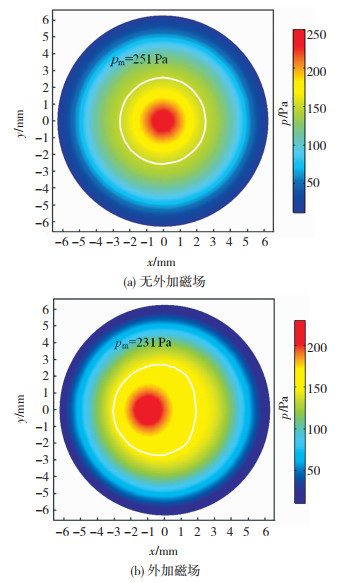
图 6为工件上表面电弧压力(p)计算结果,图中以p=150 Pa的等值线为例,对电弧压力的变化进行分析。无外加磁场时,电弧压力区域为圆形分布,压力峰值位于焊件中心;外加磁场后,电弧压力区域相应的向电弧偏转方向凹陷,电弧峰值向x负方向移动,形成向左侧凹陷的不规则形状,压力较大区域位于x负半轴。这是由于外加磁场后,电弧长度增加,造成单位长度内轴向压力差减小,导致电弧等离子体达到工件上表面的速度减小,因此,对工件表面冲击力减小[14]。
|
图 6 工件表面电弧压力分布 Fig.6 Arc pressure distribution on the workpiece surface: (a) without external magnetic field; (b) with external magnetic field |
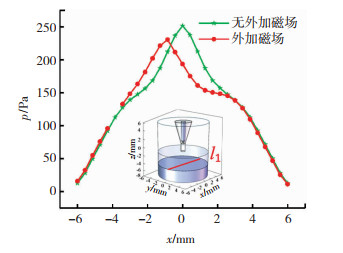
图 7为工件上表面截线l1上电弧压力的分布曲线。
|
图 7 l1上电弧压力分布曲线 Fig.7 Arc pressure distribution curve on l1 |
从图 7可以看到,无外加磁场时,在x=0处取得最大值251 Pa;外加磁场时,在x=-0.86 mm处取得最大值231 Pa。从图中曲线可以看出外加磁场使工件表面电弧压力减小,最大值降幅约为7.97%。
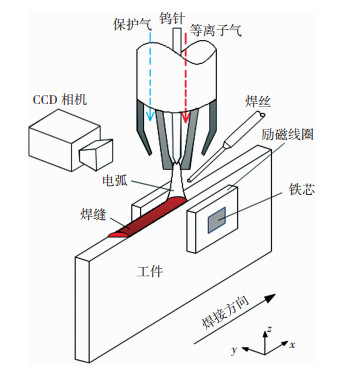
3 试验验证文中试验使用微束等离子焊接系统,选择焊接电流14 A,等离子气0.3 L/min,保护气10 L/min,堆焊时送丝速度0.13 m/min,在长宽分别为170 mm与50 mm,厚为4 mm的304不锈钢上进行焊接试验,其化学成分见文献[15]。外加稳态磁场强度为30 mT,当焊枪行至线圈边缘处打开励磁电源,离开线圈后关闭励磁电源,并使用CCD相机对焊接过程的电弧进行拍摄,试验装置示意图如图 8所示。
|
图 8 试验装置示意图 Fig.8 Schematic diagram of test device |
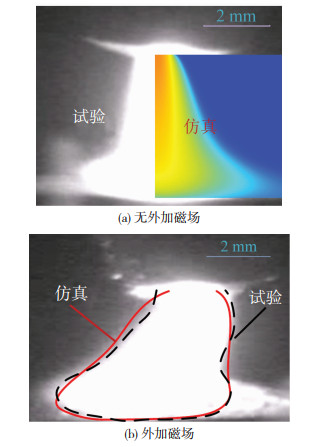
为对仿真结果加以验证,首先进行不填丝熔焊试验。电弧温度越高,释放光辐射越强,因此其光学图像可在一定程度上代表温度分布。图 9给出了试验拍摄的电弧轮廓与仿真温度场的对比,可以看到,无外加磁场时,靠近喷嘴处电弧非常集中,远离喷嘴处电弧较分散,与仿真结果基本一致;外加磁场后,喷嘴下方电弧发生与焊接方向相反(x负方向)的偏转,但由于线圈对相机角度的影响,导致拍摄到的电弧右侧工件上出现反光区域,其余轮廓与仿真结果吻合较好。
|
图 9 试验与仿真电弧轮廓对比 Fig.9 Comparison of test and simulation arc profiles: (a) without external magnetic field; (b) with external magnetic field |
按上述方法进行3层堆焊试验,并截取焊缝截面,如图 10所示,图中①为无磁场焊缝截面,②为添加磁场焊缝截面。结果表明:加磁前后堆焊层存在较大差别,无磁区域焊缝无明显分层,余高较小,熔宽较大,由截面①可见焊缝向两侧“下塌”;加磁区域焊缝存在明显分层,余高增加,熔宽减小,由截面②可见焊缝“下塌”现象消失。根据上述分析可知,外加磁场作用下电弧对焊件的热输入减小,对熔池的压力降低,使得熔池没有向两侧“下淌”,因此,焊缝“下塌”现象消失,焊缝余高增加,熔宽减小,有利于多层堆焊成形。

|
图 10 加磁前后堆焊层形貌 Fig.10 Morphologies of cladding before and after magnetization |
1) 外加横向稳态磁场后,由于喷嘴的限制,喷嘴内部电弧等离子体未发生明显变化,喷嘴下方电弧等离子体因受到洛伦兹力向x负方向移动,相应的电弧形态、电弧等离子体流速、电流密度等均发生相应的偏转。在加磁前后,电弧最高温度由14 912 K减至14 776 K,焊件表面最高温度由3 558 K降低至3 242 K;电弧等离子体流速大小无明显变化,约为192 m/s;两极之间电压由25.2 V增加至25.7 V。
2) 外加30 mT横向稳态磁场后,工件表面电弧热输入减小,最大值减小幅度约为10.5%;电弧压力降低, 最大值降幅约为7.97%。
3) 在长宽分别为170 mm与50 mm,厚为4 mm的304薄板上进行熔焊与堆焊试验,熔焊试验过程中拍摄电弧轮廓与仿真得到的电弧形态吻合度较好;堆焊层有磁区域较无磁区域焊缝余高增加、熔宽减小,且焊缝没有向两侧“下塌”,有利于多层堆焊成形。
| [1] |
KATOU M, OH J, MIYAMOTO Y, et al. Freeform fabrication of titanium metal and intermetallic alloys by three-dimensional micro welding[J]. Materials & Design, 2007, 28(7): 2093-2098. DOI:10.1016/j.matdes.2006.05.024 |
| [2] |
CHEN T, WANG C, LIAO M R, et al. Diffuse and spot mode of cathode arc attachments in an atmospheric magnetically rotating argon arc[J]. Journal of Physics D, 2016, 49(8): 085202. DOI:10.1088/0022-3727/49/8/085202 |
| [3] |
TRELLES, PABLO J. Finite element methods for arc discharge simulation[J]. Plasma Processes and Polymers, 2016, 14(1-2): 1600092. DOI:10.1002/ppap.201600092 |
| [4] |
陈树君, 徐斌, 蒋凡. 变极性等离子弧焊电弧物理特性的数值模拟[J]. 金属学报, 2017, 53(5): 631-640. CHEN Shujun, XU Bin, JIANG Fan. Numerical simulation of physical characteristics of variable polarity plasma arc welding[J]. Acta metallurgica sinica, 2017, 53(5): 631-640. DOI:10.11900/0412.1961.2016.00263 |
| [5] |
LIU Z J, LI Y H, SU Y H. Simulation and analysis of heat transfer and fluid flow characteristics of arc plasma in longitudinal magnetic field-tungsten inert gas hybrid welding[J]. The International Journal of Advanced Manufacturing Technology, 2018, 98(5-8): 2015-2030. DOI:10.1007/s00170-018-2320-3 |
| [6] |
周祥曼, 田启华, 杜义贤, 等. 外加横向磁场作用电弧增材成形过程中的传热传质仿真[J]. 机械工程学报, 2018, 54(12): 193-206. ZHOU Xiangman, TIAN Qihua, DU Yixian, et al. Simulation of heat and mass transfer in arc welding based additive forming process with external transverse magnetic Field[J]. Journal of Mechanical Engineering, 2018, 54(12): 193-206. DOI:10.13433/j.cnki.1003-8728.20180124 |
| [7] |
周祥曼, 田启华, 杜义贤, 等. 外加稳态磁场作用下的焊接电弧数值仿真[J]. 机械科学与技术, 2018, 37(7): 1068-1075. ZHOU Xiangman, TIAN Qihua, DU Yixian, et al. Numerical simulation of welding arc under external static magnetic field[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(7): 1068-1075. DOI:10.3901/JME.2018.12.193 |
| [8] |
HU J, TSAI H L. Heat and mass transfer in gas metal arc welding. Part Ⅰ: The arc[J]. International Journal of Heat and Mass Transfer, 2007, 50(5-6): 833-846. DOI:10.1016/j.ijheatmasstransfer.2006.08.025 |
| [9] |
WANG Z, YAN F, ZHAO P. Numerical simulation of the dynamic behaviors of a gas tungsten welding arc for joining magnesium alloy AZ61A[J]. Acta Metallurgica Sinica, 2013, 26(5): 588-596. DOI:10.1007/s40195-012-0187-0 |
| [10] |
KOU S, WANG Y H. Three-dimensional convection in laser melted pools[J]. Metallurgical Transactions A, 1986, 17(12): 2265-2270. DOI:10.1007/BF02645924 |
| [11] |
TANAKA M, TERASAKI H, Ushio M, et al. A unified numerical modeling of stationary tungsten-inert-gas welding process[J]. Metallurgical and Materials Transactions A, 2002, 33(7): 2043-2052. DOI:10.1007/s11661-002-0036-2 |
| [12] |
BOULOS M I, FAUCHAIS P, PFENDER E. Thermal Plasmas[M]. New York: Plenum Press, 1994: 452. DOI:10.1007/978-1-4899-1337-1
|
| [13] |
王宗杰. 熔焊方法及设备[M]. 北京: 机械工业出版社, 2007.
|
| [14] |
代大山, 宋永伦, 张慧, 等. 等离子电弧力的研究[J]. 焊接学报, 2002, 23(2): 51-54. DAI Dashan, SONG Yonglun, ZHANG Hui, et al. Study on arc force in plasma welding[J]. Transactions of the china welding institution, 2002, 23(2): 51-54. |
| [15] |
王引真, 冯雅, 孙永兴, 等. 表面纳米化与离子渗氮对304不锈钢的影响[J]. 材料科学与工艺, 2019, 27(1): 59-64. WANG Yinzhen, FENG Ya, SUN Yongxing, et al. Effect of surface nanocrystallization and plasma nitriding parameters on 304 stainless steel[J]. Materials Science and Technology, 2019, 27(1): 59-64. DOI:10.11951/j.issn.1005-0299.20170300 |
 2021, Vol. 29
2021, Vol. 29


