2. 河北工业大学 机械工程学院,天津 300401
2. School of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, China
在振动控制领域,变阻尼和变刚度是当前实现振动半主动控制的两种主要途径,力学性能可变、可调的智能材料在振动降噪领域得到了广泛的应用[1-3]。目前已用于振动控制装置设计的智能流体材料有磁流变液、电流变液、剪切增稠液等,它们均可以通过黏度的变化来实现阻尼的调控,以适应不同的外界加载情况[4-5]。电/磁流变液装置工作时在外部激励下,通过改变电场或磁场来改变材料的黏度特性[6-7]。与电/磁流变液相比,剪切增稠液的流变力学特性随所受到外载荷的剪切速率的变化而变化,不需要外部激励。
剪切增稠液是一种纳米颗粒悬浮液,通常情况下处于流体状态,在一定的外载作用下其黏度会迅速增大甚至达到类固态,当撤去外力时,其又能恢复到流体状态[8-9]。在剪切增稠过程中,其黏度能迅速发生几个量级的改变,从而耗散大量的能量。剪切增稠液显著的能量耗散特性以及无源、自适性等特点,使得其在阻尼器、减振和振动控制装置等方面有着广阔的应用前景[10-11]。
通常剪切增稠液振动控制装置的工作模式有阀模式、剪切模式、挤压模式三种[12-14]。与阀模式和剪切模式相比,在挤压模式下智能流体材料能够产生更大的阻尼力,且具有小位移大阻尼的特点[15-16]。研究剪切增稠液的挤压流动力学性能有助于开发挤压模式下基于剪切增稠液的高性能装置。Gong等人[17]制备了不同体积分数的基于SiO2颗粒的剪切增稠液,并研究了体积分数、挤压速度等对其挤压流动行为的影响,发现随着体积分数的增大或挤压速度的增大,法向应力显著增大。
当前的研究均是以纯剪切增稠液为研究对象,开发具有更高性能的剪切增稠液可为提升振动控制装置性能提供材料基础。最近,研究人员通过在纯剪切增稠液中添加不同类型的微/纳米颗粒添加剂的方法来制备具有更高剪切增稠效应的新型剪切增稠液[18-20]。Laha等人[18]的研究结果表明,与纯剪切增稠液相比,Kevlar织物在用含埃洛石纳米管添加剂的SiO2基剪切增稠液浸渍后,抗冲击性能有了明显的改善。Tan等人[19-20]研究了高应变率下SiC纳米线增强后的剪切增稠液和石墨烯增强后的剪切增稠液的动态力学响应,结果表明增强后的剪切增稠液可以承受比纯剪切增稠液更大的动态载荷。
随着高性能振动控制装置的开发,对剪切增稠液的力学性能提出了更高的要求,因此有必要开发和制备高性能的新型剪切增稠液。本文采用石墨烯增强纯二氧化硅纳米颗粒剪切增稠液,并利用旋转流变仪对不同的剪切增稠液开展了挤压流动实验,研究了石墨烯对剪切增稠液的流变性能和挤压流动力学性能的影响,分析了石墨烯体积分数对法向应力、临界间隙和承载能力的影响,为剪切增稠液在振动控制领域的应用提供基础。
1 实验测试分析 1.1 材料制备本文中以纳米二氧化硅颗粒作为分散相,聚乙二醇400(PEG400) 作为分散介质来制备剪切增稠液。纳米级二氧化硅球形颗粒由Stober方法制备,直径约为300 nm,如图 1(a) 所示。利用球磨的方法将纳米二氧化硅颗粒分散入PEG400中,制备得到体积分数为56%剪切增稠液样品。多层石墨烯(厚度为10~15层,长度或宽度约为800 nm,由南京先丰纳米材料有限公司生产,如图 1(b) 所示)以超声分散的方式分散到纯剪切增稠液中,以改变其流变性能。为了分析石墨烯体积分数对剪切增稠液挤压流动力学性能的影响,制备了不同体积分数石墨烯增强的剪切增稠液,剪切增稠液中固相的体积分数为56%,如表 1所示。

|
图 1 分散相颗粒扫描电子显微镜图 Fig.1 SEM images of solid phase in STFs: (a) SiO2 nanoparticle; (b) grapheme |
| 表 1 不同剪切增稠液中分散相含量(体积分数/%) Table 1 Content of the solid phase in different STFs |
实验中采用旋转流变仪(Anton-Paar MCR 302)与CP25-2锥形板测试附件、PP50平行板测试附件(见图 2)测试剪切增稠液的流变性能和挤压流动力学性能。

|
图 2 旋转流变仪和平行板测试附件 Fig.2 Rotary rheometer and parallel plate accessory |
作为典型的非牛顿流体,通常采用平行圆板匀速挤压等体积样品的方式来研究剪切增稠液的挤压流动力学性能,如图 3所示。这种挤压形式常出现在阻尼器和隔振器的服役过程中。在测试中,样品的直径始终小于平行圆板的直径,平行圆板之间的剪切增稠液样品体积保持不变。

|
图 3 等体积挤压流动示意图 Fig.3 Squeeze flow with constant volume of sample between the plates |
通过稳态剪切实验来测试剪切增稠液的流变性能,剪切速率范围为0.01~100 s-1。采用等体积挤压的方式对不同的剪切增稠液进行挤压流动实验,样品体积为0.4 mL,平行板初始间隙设定为1.2 mm。如图 3所示,在测试中,下平板固定,上平板以恒定的速度向下挤压剪切增稠液,当法向力达到50 N(流变仪可承受的最大法向力)时,上平板开始以相同的速度向上拉伸剪切增稠液,直至回到初始位置,测试过程分为挤压和拉伸两个阶段,流变仪记录挤压-拉伸过程中法向力随着板间距的变化。
测试之前对剪切增稠液样品进行预剪切处理,以使其内部颗粒达到均匀稳定的状态,从而消除加载过程对剪切增稠液流变性能的影响,保证测试结果的可靠性。本文通过恒定剪切速率的稳态剪切来实现剪切增稠液样品的预剪切处理,剪切速率1 s-1,预剪切时间60 s。
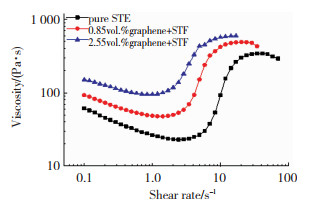
2 结果与讨论 2.1 石墨烯对剪切增稠液流变性能的影响对3种不同的剪切增稠液(表 1中)进行了流变性能测试,其黏度曲线如图 4所示。从图 4中可以看出不同剪切增稠液的黏度曲线具有相似的变化趋势,均包含剪切变稀和剪切增稠两个阶段。但石墨烯增强剪切增稠液的黏度大于纯剪切增稠液,且随着石墨烯体积分数的增加,剪切增稠液的黏度变大。在初始阶段,体积分数为0.85%和2.55%的石墨烯增强剪切增稠液的初始黏度分别为92.771 Pa·s和150.98 Pa·s,分别是纯剪切增稠液的初始黏度61.181 Pa·s的1.52倍、2.47倍。在剪切增稠阶段,石墨烯增强剪切增稠液的黏度峰值分别为492.12 Pa·s、599.42 Pa·s,比纯剪切增稠液的黏度峰值344.24 Pa·s最多增加了74%。
|
图 4 不同剪切增稠液的黏度曲线 Fig.4 The viscosity curves of different STFs |
在初始阶段,由于纳米颗粒的存在使得剪切增稠液具有一定的黏度。随着剪切速率的增加,纳米颗粒之间的流体润滑力增大,这使得纳米颗粒逐渐排列成最有利于其相互运动的层状结构,剪切增稠液的黏度降低。随着剪切速率继续增加,逐渐增大的流体润滑力使剪切增稠液中形成粒子簇,进而导致剪切增稠现象的发生[21]。而在增强剪切增稠液中,石墨烯可等效为板状,因此在石墨烯增强剪切增稠液中,流体动力润滑力存在于SiO2纳米颗粒之间、SiO2纳米颗粒与石墨烯之间以及石墨烯之间,三种润滑力的共同作用显著提高了剪切增稠液的黏度。
2.2 挤压速度对法向应力的影响在挤压模式下,法向力作为剪切增稠液弹性性能的重要体现,对于评价剪切增稠液的挤压流动力学性能和理解剪切增稠液的微观结构变化有
着重要的作用;此外对剪切增稠液法向力的研究有着重要的工程应用价值,利用法向力设计的新型剪切增稠液装置具有更小的尺寸。因此在挤压流动实验中,法向力被重点关注且被用于表征剪切增稠液的挤压流动力学性能[17, 22]。
在等体积挤压过程中,剪切增稠液试样的横截面积逐渐增大,因此法向应力比法向力更适合用来描述挤压模式下剪切增稠液的流动行为。因此本文通过法向应力与平行板间隙的关系来表征剪切增稠液的挤压流动力学性能。法向应力的计算公式为
| $ \sigma = \frac{{{F_{\rm{N}}}}}{{V/h}} $ | (1) |
式中: σ为法向应力,kPa;FN为法向力,N;V为试样品的体积,mL;h为平行板的间距,mm。
根据挤压流动理论可知,挤压过程中法向的压缩和径向的流动使得剪切增稠液中产生法向应力和剪切应力,而剪切增稠液中的剪切应力和法向应力源自于纳米颗粒之间的流体动力润滑力[23]。球状SiO2纳米颗之间的流体润滑力可以表示为[24]
| $ {F_{{\rm{sphere - sphere }}}} = \frac{{6\pi \eta U{r^2}}}{h} $ | (2) |
式中: Fsphere-sphere为两个球状颗粒之间的流体润滑力,N;r为球状颗粒的半径,m;h为球状颗粒之间的距离,m;U为球状颗粒之间的相对速度,m/s,η为颗粒间隙中流体的黏度,Pa·s。
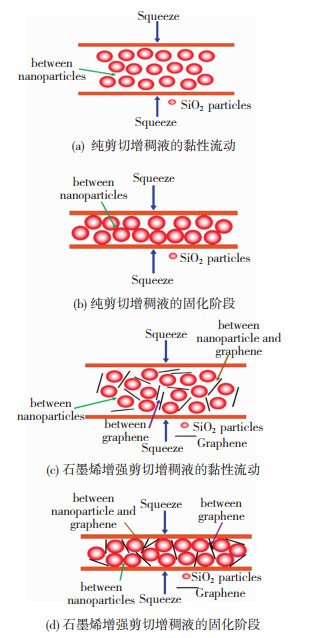
图 5为剪切增稠液的典型挤压流动曲线,测试样品为纯剪切增稠液,挤压速度为90 μm/s。从图 5中可以看出在挤压模式下,剪切增稠液要经历自由扩散、黏性流动和固化3个阶段。定义挤压速率为挤压速度与板间隙的比值。在自由扩散阶段,挤压速率较慢,剪切增稠液处于自由流动状态,法向应力几乎不变。在黏性流动阶段,随着平板间隙的减小,挤压速率逐渐增大,剪切增稠液中纳米颗粒的分布开始发生变化,颗粒之间的距离逐渐变小。由式(2)可知,挤压速率的增大和颗粒间距的减小共同导致纳米颗粒之间的流体动力润滑力增大,进而使得法向应力开始上升,如图 6(a)所示。在固化阶段,快速的压缩作用使得颗粒间距迅速变小,颗粒逐渐接触并产生接触力,随着平板间隙的继续减小,相互接触的颗粒形成网状结构,剪切增稠液的扩散受到阻碍,当网状结构与上下板边界接触时,剪切增稠液中发生阻塞现象,法向应力迅速增加,如图 6(b)所示。

|
图 5 剪切增稠液的典型挤压流动曲线 Fig.5 A typical squeeze curve of STF |
|
图 6 挤压模式下不同的剪切增稠液内部的颗粒结构变化示意图 Fig.6 Schematic illustrations of the structure evolution under squeeze: (a)viscous flow of Pure STF; (b) curing stage of Pure STF; (c)viscous flow of graphene reinforced STF; (d)curing stage of graphene reinforced STF |
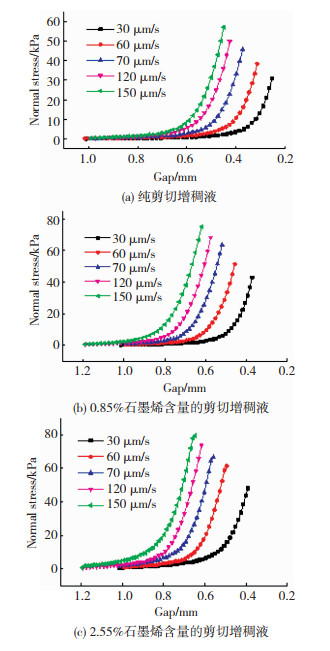
图 7为不同挤压速度下3种剪切增稠液的挤压流动曲线,可以看出,在不同的挤压速度下,其挤压流动曲线具有相似的变化趋势:随着挤压速度的增大,临界间隙、法向应力和极限间隙均呈上升的趋势。随着挤压速度的增大,相同间隙处的挤压速率增大,挤压速率的快速变化导致纳米颗粒的分布迅速发生变化,挤压过程提前进入黏性流动阶段,临界间隙增大;此外挤压速率的增大导致颗粒间相互作用增强,流体动力润滑力和接触力增大,进而使得法向应力增大,与此同时,挤压力达到极限值50 N时只需更短的挤压行程,极限间隙增大。
|
图 7 不同挤压速度下法向应力随板间距的变化 Fig.7 The change in normal stress with gap distance for different squeeze velocities: (a) pure STF; (b) STF with 0.85vol.% graphene; (c) STF with 2.55vol.% graphene |
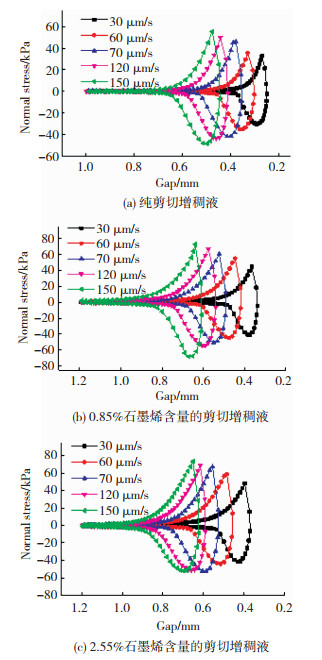
图 8为不同挤压速度下3种剪切增稠液的挤压-拉伸流动曲线,可以看出,在不同速度下,3种剪切增稠液的挤压-拉伸流动曲线均是近似对称的。在拉伸过程中,随着板间距的增大,剪切增稠液中的网状结构逐渐消失,颗粒之间的相互作用逐渐降低直至恢复到初始状态,此时拉伸可以看做是挤压的卸载过程,剪切增稠液经历固化、黏性流动恢复到自由流动状态。此外,在挤压-拉伸过程中,3种剪切增稠液的挤压应力峰值均略高于拉伸应力峰值。这主要归因于在平行板与剪切增稠液界面上存在一个极限拉伸应力,当界面应力达到极限拉伸应力时,平行板局部会出现“拉伸滑脱”现象。
|
图 8 不同速度下三种剪切增稠液的挤压-拉伸流动曲线 Fig.8 The squeeze-tensile flow curves of three STFS at different velocities: (a) pure STF; (b) STF with 0.85vol.% graphene; (c) STF with 2.55vol.% grapheme |
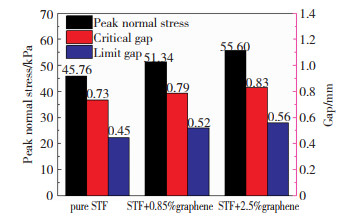
图 9显示了挤压模式下含有不同体积分数石墨烯的3种剪切增稠液的法向应力、临界间隙和极限间隙,挤压速度为90 μm/s。从图 9中可以发现,石墨烯对剪切增稠液的挤压流动力学性能有显著的影响,与纯剪切增稠液相比,石墨烯增强剪切增稠液的法向应力、临界间隙和极限间隙明显增大,且随着石墨烯体积分数的增大而增大。
|
图 9 不同剪切增稠液的法向力峰值、临界间隙和极限间隙 Fig.9 The peak normal stress, critical gap, limit gao of different STFs |
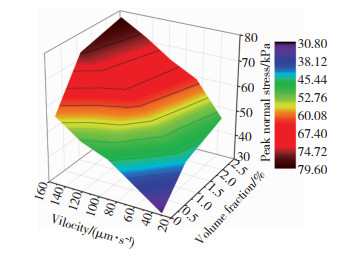
图 10显示了挤压速度和石墨烯体积分数对剪切增稠液法向应力峰值的综合效应,在较高挤压速度和较大石墨烯体积分数的挤压工况下,剪切增稠液的法向应力峰值明显增大。当挤压速度为150 μm/s、石墨烯体积分数为2.55%时,法向应力峰值可达79.6 kPa,是Gong等[18]报道的纯剪切增稠液的法向应力峰值38.48 kPa的2.07倍。这表明,与纯剪切增稠液相比,石墨烯增强剪切增稠液在挤压模式下的承载能力得到显著提高。
|
图 10 挤压速度和石墨烯体积分数对剪切增稠液法向应力峰值的综合效应 Fig.10 Combined effect of squeeze velocity and graphene volume fraction on the normal stress |
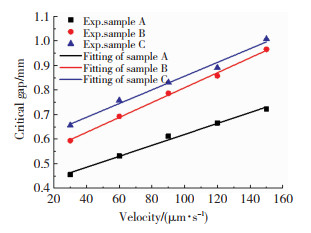
图 11显示了不同挤压速度下3种剪切增稠液的临界间隙。从图 11中可以发现,临界间隙d随着挤压速度v的增大而线性增大,因此二者的关系可表示为
| $ d = \alpha v + {d_0} $ | (3) |
|
图 11 不同挤压速度下3种剪切增稠液的临界间隙 Fig.11 The critical gap of three STFS at different velocities |
式中: d0为挤压速度极小时的临界间隙,mm;α为挤压速度对临界间隙的影响系数。
利用式(3)对实验结果进行拟合,由拟合结果可知,石墨烯增强剪切增稠液的影响系数比纯剪切增稠液的大,纯剪切增稠液的影响系数α1为0.002 23,石墨烯体积分数为0.85% 和2.55%的影响系数α2、α3分别为0.003 03、0.002 79。这表明,相比于纯剪切增稠液,石墨烯增强剪切增稠液的挤压流动行为对挤压速度的变化更加敏感。
2.4 石墨烯体积分数对挤压流动力学性能影响的机理分析本文所有测试中均控制最大法向力不变,因此不同测试工况下的挤压行程不同。而衡量材料的能量吸收性能,应以相同挤压行程中材料吸收的能量值为标准。所以,本文定义平均能量吸收值E为:
| $ \bar E = \frac{{\int {{F_{\rm{N}}}} {\rm{d}}s}}{s} $ | (4) |
| $ {F_{\rm{N}}}{\rm{ = }}\sigma V/h $ | (5) |
式中,E为平均能量吸收值,10-3 J/mm;FN为法向力,N;s为挤压行程,mm;V为剪切增稠液的体积,mL;h为平行板的间隙,mm。
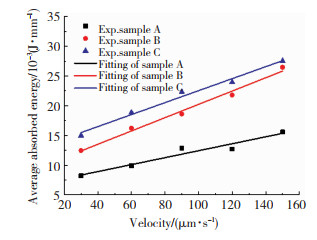
图 12显示了不同挤压速度下3种剪切增稠液的平均能量吸收值,在相同挤压速度下,石墨烯增强剪切增稠液的平均能量吸收值大于纯剪切增稠液,且随着石墨烯体积分数的增加而增大。这表明石墨烯显著提升了剪切增稠液的能量吸收性能。此外剪切增稠液的平均能量吸收值E随着挤压速度v的增大而线性增大,二者的关系可表示为:
| $ \bar E = Bv + \overline {{E_0}} $ | (6) |
|
图 12 不同挤压速度下3种剪切增稠液的平均能量吸收值 Fig.12 The average absorbed energy of three STFS at different velocities |
式中:
利用式(6)对实验结果进行拟合,由拟合结果可知,石墨烯增强剪切增稠液的影响系数比纯剪切增稠液的大,纯剪切增稠液的影响系数β1为0.058 51,体积分数为0.85% 和2.55%的石墨烯增强剪切增稠液的影响系数β2、β3分别为0.111 93、0.100 8。这表明与纯剪切增稠液相比,石墨烯增强剪切增稠液有更强的速度敏感性。
在石墨烯增强剪切增稠液中,板状石墨烯均匀分散在球状SiO2纳米颗粒之间,石墨烯能够有效地阻碍纳米颗粒的滑动,使得纳米颗粒在径向扩散缓慢,因此挤压过程进入黏性流动阶段只需更短的挤压行程,临界间隙增大。此外,如图 6(c)所示,石墨烯增强剪切增稠液的流体润滑力分别存在于纳米颗粒之间、纳米颗粒与石墨烯之间以及石墨烯之间。而纳米颗粒之间的流体润滑力如式(2)所示,纳米颗粒与石墨烯之间、石墨烯与石墨烯之间的流体润滑力分别可以表示为[24-25]:
| $ {F_{{\rm{sphere - plate }}}} = \frac{{6{\rm{ \mathsf{ π} }}\eta Ur}}{h}(h + r) $ | (7) |
| $ {F_{{\rm{plate - plate }}}} = \frac{{6{\rm{ \mathsf{ π} }}\eta U{r^2}}}{h}{\left( {\frac{r}{{4h}}} \right)^2} $ | (8) |
式中: Fsphere-plate、Fplate-plate分别为球状颗粒与平板之间、两个平板之间的流体润滑力,N;r为球体颗粒或平板的半径,m;h为球体颗粒或平板之间的距离,m;U为颗粒或平板之间的相对速度,m/s;η为间隙中流体的黏度,Pa·s。
在挤压流实验中,h≥r,对比式(2)、式(7)和式(8),3种流体动力润滑力的大小顺序为:Fplate-plate>Fsphere-plate>Fsphere-sphere,因此石墨烯可以增大剪切增稠液的流体动力润滑力,进而使得法向应力增大。在固化阶段,如图 6(d)所示,由于石墨烯对纳米颗粒滑动的限制,石墨烯增大了网状结构的紧密性和稳定性,其能够有效地防止网状结构的断裂与滑移,从而使得石墨烯增强剪切增稠液中纳米颗粒之间的接触力增大,法向应力增大。这意味着石墨烯能够显著影响剪切增稠液的挤压流动性能,因此当挤压速度发生变化时,石墨烯增强剪切增稠液的力学响应比纯剪切增稠液更加明显,即石墨烯增强剪切增稠液对挤压速度的变化更加敏感。
3 结论1) 石墨烯显著影响了剪切增稠液的流变性能,石墨烯增强剪切增稠液的黏度峰值为599.42 Pa·s,与纯剪切增稠液相比提高了74%。
2) 石墨烯增强剪切增稠液在挤压模式下的承载能力得到显著提高,其法向应力峰为纯剪切增稠液的2.07倍。这主要归因于石墨烯能有效地阻碍纳米颗粒的滑动以及石墨烯与石墨烯之间、石墨烯与颗粒之间所存在的流体润滑力。
3) 在挤压速度增大或石墨烯体积分数增大的挤压工况下,剪切增稠液的法向应力和临界间隙均明显增大。相较于挤压速度30 μm/s下的纯剪切增稠液,挤压速度90 μm/s下石墨烯增强剪切增稠液的法向应力峰值增大了158%,临界间隙增大了122%。
| [1] |
TANG H, ZHAO X P, LIU S. Design and performance research of an adaptive damper composed of electrorheological fluids and piezoelectric ceramics[J]. Smart Materials and Structures, 2003, 12(3): 347-354. DOI:10.1088/0964-1726/12/3/305 |
| [2] |
ZHU X, JING X, CHENG L. Magnetorheological fluid dampers: a review on structure design and analysis[J]. Journal of Intelligent Material Systems and Structures, 2012, 23(8): 839-873. DOI:10.1177/1045389X12436735 |
| [3] |
吕宏展, 梁锡昌, 王家序, 等. 新型稳定磁流变体材料-磁胶的性能实验研究[J]. 材料科学与工艺, 2011, 19(1): 139-143. LU Hongzhan, LIANG Jiachang, WANG Jiaxu, et al. Performance test study on a new type of magnetorheological material-magnetic colloid[J]. Materials Science & Technology, 2011, 19(1): 139-143. DOI:10.11951/j.issn.1005-0299.20110128 |
| [4] |
张永亮, 于骏, 王茂华. 电流变液减振器及其在切削颤振控制中应用的研究现状[J]. 振动与冲击, 2003, 22(2): 14-17. ZHANG Yongliang, YU Jun, WANG Junhua. Electrorheological vibtation damper and their applications in machining chatter control: a survey[J]. Journal of Vibration and Shock, 2003, 22(2): 14-17. DOI:10.13465/j.cnki.jvs.2003.02.005 |
| [5] |
LI W H, DU H. Design and Experimental Evaluation of a Magnetorheological Brake[J]. International Journal of Advanced Manufacturing Technology, 2003, 21(7): 508-515. DOI:10.1007/s001700300060 |
| [6] |
WERELEY N M, LINDLER J, ROSENFELD N, et al. Biviscous damping behavior in electrorheological shock absorbers[J]. Smart Materials and Structures, 2004, 13(4): 743-752. DOI:10.1088/0964-1726/13/4/012 |
| [7] |
ZHANG X, LI W, GONG X L. Study on magnetorheological shear thickening fluid[J]. Smart Materials and Structures, 2008, 17(1): 015051. DOI:10.1088/0964-1726/17/1/015051 |
| [8] |
FALL A, BERTRAND F, OVARLEZ G, et al. Shear thickening of cornstarch suspensions[J]. Journal of Rheology, 2012, 56(3): 575-0. DOI:10.1122/1.3696875 |
| [9] |
SWARNA, PATTANAYEK S K, GHOSH A K. Dynamic shear rheology of colloidal suspensions of surface-modified silica nanoparticles in PEG[J]. Journal of Nanoparticle Research, 2018, 20(3): 53-59. DOI:10.1007/s11051-017-4121-2 |
| [10] |
周鸿, 郭朝阳, 宗路航, 等. 剪切增稠液及阻尼器性能研究[J]. 振动与冲击, 2013, 32(18): 15-20. ZHOU Hong, GUO Chaoyang, ZONG Luhang, et al. Performance of shear thickening fluid and a damper as its application[J]. Journal of Vibration and Shock, 2013, 32(18): 15-20. DOI:10.13465/j.cnki.jvs.2013.18.007 |
| [11] |
QIAN Z, YONG H H, HONG L Y, et al. Dynamic performance and mechanical model analysis of a shear thickening fluid damper[J]. Smart Materials and Structures, 2018, 27(7): 075021. DOI:10.1088/1361-665X/aac23f |
| [12] |
SEE H. Field dependence of the response of a magnetorheological suspension under steady shear flow and squeezing flow[J]. Rheologica Acta, 2003, 42(1-2): 86-92. DOI:10.1007/s00397-002-0258-7 |
| [13] |
ZHU X C, JING X J, CHENG L. Magnetorheological fluid dampers: a review on structure design and analysis[J]. Journal of Intelligent Material Systems and Structures Intell, 2012, 23(8): 839-873. DOI:10.1177/1045389X12436735 |
| [14] |
YAZID I I M, MAZLAN S A, KIKUCHI T, et al. Design of magnetorheological damper with a combination of shear and squeeze modes[J]. Materials & Design, 2014, 54(54): 87-95. DOI:10.1016/j.matdes.2013.07.090 |
| [15] |
TIAN Y, MENG Y, MAO H, et al. Electrorheological fluid under elongation, compression, and shearing[J]. Physical Review E, 2002, 65(3): 031507. DOI:10.1103/PhysRevE.65.031507 |
| [16] |
DE VICENTE J, KLINGENBERG D J, HIDALGO-ALVAREZ R. Magnetorheological fluids: a review[J]. Soft Matter, 2011, 7(8): 3701-3710. DOI:10.1039/c0sm01221a |
| [17] |
GONG X L, CHEN Q, LIU M, et al. Squeeze flow behavior of shear thickening fluid under constant volume[J]. Smart Materials and Structures, 2017, 26(6): 065017. DOI:10.1088/1361-665X/aa6ef0 |
| [18] |
LAHA A, MAJUMDAR A. Shear thickening fluids using silica-halloysite nanotubes to improve the impact resistance of p-aramid fabrics[J]. Applied Clay Science, 2016, 132: 468-474. DOI:10.1016/j.clay.2016.07.017 |
| [19] |
TAN Z H, GE J H, ZHANG H, et al. Dynamic response of shear thickening fluid reinforced with SiC nanowires under high strain rates[J]. Applied Physics Letters, 2017, 111(3): 031902. DOI:10.1063/1.4994066 |
| [20] |
TAN Z H, MA H Q, ZHOU H, et al. The influence of graphene on the dynamic mechanical behaviour of shear thickening fluids[J]. Advanced Powder Technology, 2019, 30(10): 2416-2421. DOI:10.1016/j.apt.2019.07.025 |
| [21] |
WAGNER N J, BRADY J F. Shear thickening in colloidal dispersions[J]. Physics Today, 2009, 62(10): 27-32. DOI:10.1063/1.3248476 |
| [22] |
SELIM G, KUSHAN M C, LI W H. Shear thickening fluids in protective applications: A review[J]. Progress in Polymer Science, 2017, 75: 48-72. DOI:10.1016/j.compositesa.2016.06.006 |
| [23] |
COLLYER A A, CLEGG D W. Rheological measurement[M]. London: Chapman & Hall, 1998: 550-592. DOI:10.1007/978-94-011-4934-1_9
|
| [24] |
BARNOCKY G, DAVIS R H. The lubrication force between spherical drops, bubbles and rigid particles in a viscous fluid[J]. International Journal of Multiphase Flow, 1989, 15(4): 627-638. DOI:10.1016/0301-9322(89)90057-8 |
| [25] |
KAVEH F, ALLY J, KAPPL M, et al. Hydrodynamic force between a sphere and a soft, elastic surface[J]. Langmuir, 2014, 30(39): 11619-11624. DOI:10.1021/la502328u |
 2021, Vol. 29
2021, Vol. 29


