油气管道在国家经济运行和人们日常生活中发挥着极其重要的作用。统计发现,油气管道的破坏主要源于各种微观和宏观的应力集中[1]。其中,塑性变形被认为是材料在破坏前必经的一个特殊阶段,可以看作是材料在应力作用下的一种早期损伤状态。因此,进行管道的塑性变形检测,可以实现对管道损伤的早期预警,以保证油气运输管道高效安全的运行。
20世纪末兴起的金属磁记忆检测技术,是一种通过检测铁磁性材料在地磁场和应力作用下的磁记忆信号,来发现应力集中和缺陷损伤的无损检测方法[2-3]。利用磁记忆检测实现塑性变形诊断是一项新技术,目前对这一技术的研究还很有限。在试验研究方面,由于采用的检测设备不同,磁记忆信号在不同变形阶段的表现特征存在许多差异,磁场分量的选择也有不同观点。Dong等[4]研究了18CrNiWA钢在弹塑性变形阶段的磁记忆信号法向分量的变化规律,发现斜率在屈服极限时达到最大值;易术春等[5]通过对Q345B钢静载拉伸实验研究,建立了法向磁场梯度指数与应力的量化关系;李云飞等[6]研究了X80管线钢拉伸载荷下的磁记忆信号的法向和切向分量特征,以及与塑性损伤程度之间的关系。目前,多数研究工作集中在拉伸载荷作用下法向磁场分量的特征研究,但对切向分量的研究鲜有报道。在磁记忆机理研究方面,利用J-A理论模型来描述弹性变形已得到广泛认可,但由于塑性变形对磁化的影响因素非常复杂,不同学者也提出了不同的理论模型。Sablik等[7]利用残余应力来替换作用应力,对J-A模型进行了改进;Wang等[8]提出了磁有效场的塑性变形分量,得到非滞后磁化强度与塑性应变之间的定量关系;刘清友等[9]在对比分析多种塑性变形磁化模型表达式的基础上,推导出塑性变形的修正磁化模型。可见,塑性阶段的力-磁定量关系目前尚无统一定论。
针对以上问题,本文通过X80管线钢的静载拉伸试验,得到在弹塑性变形状态下试件表面的磁信号变化规律,研究了相应的力磁耦合机理,建立了特征参数与应力的量化关系,以期为塑性变形损伤的诊断和预测提供一定的理论基础。
1 金属磁记忆检测原理金属磁记忆检测是以地磁场作为励磁源的一种弱磁检测技术,其基本原理是:在地磁场和外应力的共同作用下,铁磁构件应力集中区的内部磁畴,发生具有磁致伸缩现象的磁畴晶格组织定向和不可逆的重新取向,并在应力与变形集中区形成附加磁极[10], 宏观显示为构件周围磁场的异常,即应力集中区的磁信号切向分量出现极值,法向分量改变符号且在异常区具有零值[11], 如图 1所示。由于金属内部存在内耗效应(粘弹性,位错内耗等), 使得外应力消除后,这种磁状态的不可逆变化继续保留。因此,通过对构件表面磁场的检测,可以对其应力集中情况进行定位和评价,从而达到早期诊断的目的。
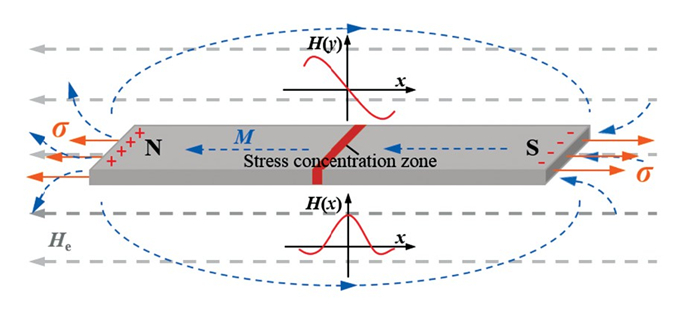
|
图 1 磁记忆检测原理图 Fig.1 Schematic diagram of magnetic memory testing |
试验采用国内某钢厂生产的X80管线钢,其主要化学成分如表 1所示。通过拉伸性能测试,得到材料的力学性能参数如表 2所示。根据GB/T228.1-2010加工的标准板状试件尺寸如图 2所示。为减少测量路径和提离值对磁记忆信号的影响,在标准板状试件上布置限位块和扫描线。
| 表 1 X80管线钢的化学成分(质量分数/%) Table 1 Chemical composition of X80 pipeline steel (wt.%) |
| 表 2 X80管线钢的力学性能 Table 2 Mechanical parameters of X80 pipeline steel |
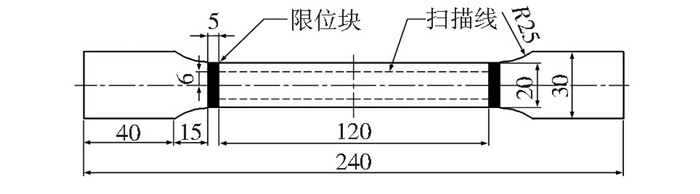
|
图 2 检测试件示意图(单位: mm) Fig.2 Schematic diagram of the test specimen |
为避免试件在加工过程中造成的应力集中对试验结果产生影响,采用TC-3台式退磁器对试件进行退磁处理。静载拉伸试验在MTS-809.25疲劳试验机上完成,采用逐级加载的方式进行施载,达到预定值后,保载10 s再取下试件,用TSC-2M-8磁记忆检测仪进行试件表面磁场强度扫描,测试提离值保持2 mm不变,测试方向和地磁南北极方向垂直。依此重复,直至试件被拉断。
3 试验结果为了消除测试误差,选用3组相同试样,在相同测试条件下进行了重复试验。通过数据分析发现,各试件的磁场分量信号,以及同一试件两条扫描线上的磁场分量值均具有很高的相似度。因此,选取其中一个试件作为研究对象,其检测结果取两条扫描线上磁场分量值的平均值。
3.1 载荷与变形阶段的关系拉伸试件的载荷应变曲线如图 3所示。在加载过程中,试样经历了弹性变形-屈服-塑性变形的不同阶段。根据载荷(F)-应变(ε)曲线,可以初步确定拉伸载荷与变形阶段的对应关系。但在逐级加载试验中,反复加载将导致试件疲劳积累,使得屈服载荷发生变化,而无法准确划分变形阶段。通过记录拉伸试件加载时和卸载后的位移,可得到试件的载荷(F)-伸长量(ΔL)曲线,如图 4所示。
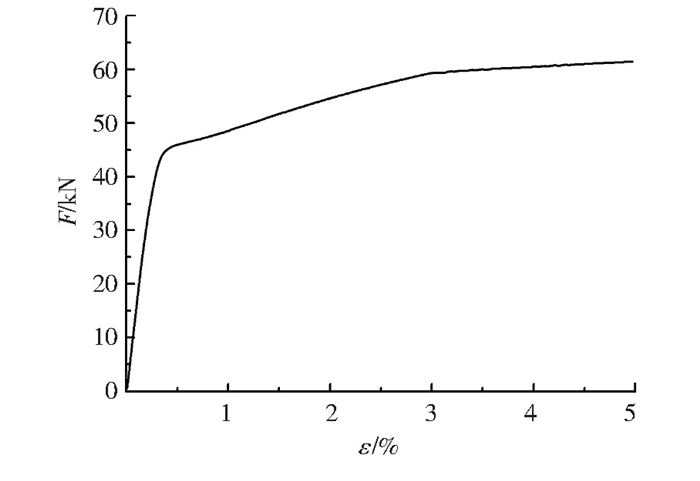
|
图 3 试件的载荷-应变曲线 Fig.3 Load-strain curve of specimen |
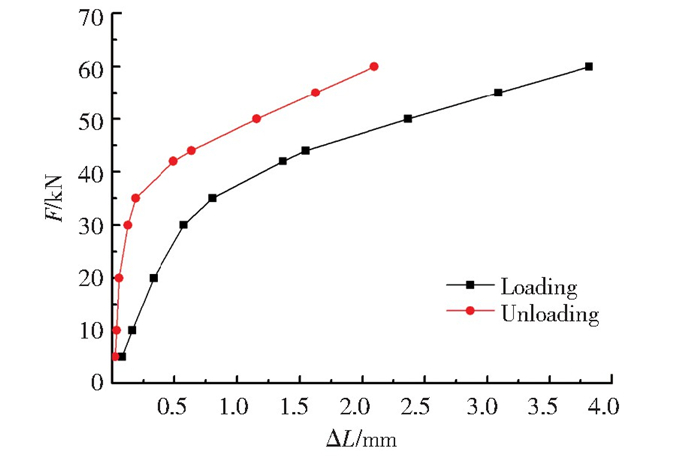
|
图 4 试件的载荷-伸长量曲线 Fig.4 Load-elongation curve of specimen |
试件伸长量随载荷变化的过程明显分成两个阶段:当载荷F≤35 kN时,试件的总伸长量较小,卸载后的残余伸长量几乎为零,表现出弹性变形特征;当载荷F≥42 kN时,试件的总伸长量和残余伸长量均随载荷的增加而显著增大,表现出塑性变形特征。结合图 3和图 4的检测结果,在弹性变形阶段选取的拉伸载荷分别为5、10、20、30和35 kN; 在塑性变形阶段选取的拉伸载荷分别为42、44、50和55 kN。
3.2 载荷对磁场分量的影响 3.2.1 弹性阶段对试件逐级加载至预定载荷,卸载后进行磁记忆检测,获得了不同载荷下试件表面的磁场强度分布曲线。如图 5所示,在弹性变形阶段,随扫描位移量Lx的增加,磁记忆信号的法向分量H(y)和切向分量H(x)均表现为线性程度较好的直线。由于材料内部应力分布相对均匀,因此,各载荷作用下的磁场强度分布曲线具有相似特征。其中,法向分量H(y)表现为倾斜的直线,随载荷的增加逆时针偏转,逐渐变陡;切向分量H(x)表现为水平直线,随载荷的增加逐渐下移。
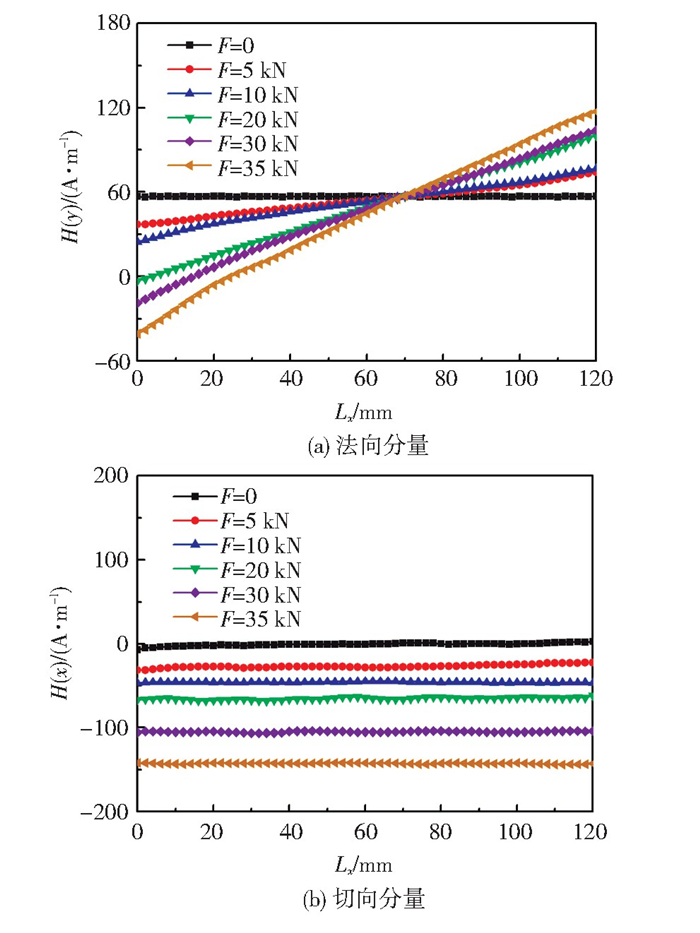
|
图 5 弹性变形阶段载荷对磁信号的影响 Fig.5 Effect of load on magnetic signal in elastic deformation stage: (a) normal component; (b) tangential component |
为进一步研究X80管线钢在塑性变形状态下的磁记忆信号变化规律,分别检测了试件逐级加载后的表面磁场强度。如图 6(a)所示,各载荷作用下的H(y)曲线团聚在一起,随着拉伸载荷的增加,其斜率略微减小,相比于弹性阶段的磁信号出现了反转现象;H(y)曲线在Lx=10~30 mm区域内出现了不同程度的波动。进一步研究法向分量的梯度K(y)(图 6(b)), 发现在该区域存在明显的不均匀变化,说明此处存在磁场强度的畸变。如图 6(c)所示,切向分量H(x)在各载荷作用下的曲线近似于水平直线,随着拉伸载荷的增加而逐渐上移,并在Lx=10~30 mm区域内出现明显弯曲,其变形程度随载荷的增加而增大。切向分量的梯度K(x)曲线在此范围内表现出过零点特征(图 6(d))。由Doubov教授的判据[3-11]可知,试件出现了明显的应力集中情况。观察试件表面发现,在Lx=10~30 mm区域内出现明显的滑移线,这是塑性变形的应变痕迹。上述试验现象说明,磁场强度分布曲线的畸变区域与试件的塑性变形区相对应。
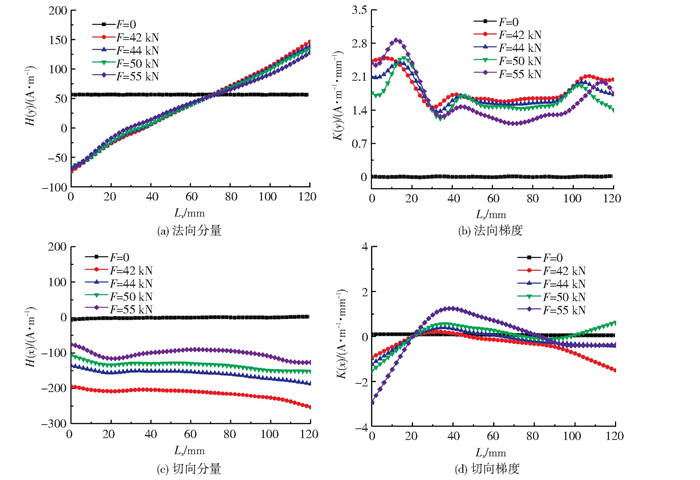
|
图 6 塑性变形阶段载荷对磁信号及其梯度的影响 Fig.6 Effect of load on magnetic signal and gradient in plastic deformation stage: (a) normal component; (b) normal gradient; (c) tangential component; (d) tangential gradient |
根据3组重复试验的检测结果,分别提取磁场强度法向分量的斜率Ks(y)和切向分量的绝对值|H(x)|, 绘制两特征参数与拉应力σ的关系曲线,结果如图 7、图 8所示。由图 7、图 8可以看出,Ks(y)和|H(x)|随拉应力σ的变化规律表现出相似的特征:弹性变形阶段,两个特征参数随应力的增加而快速增大;达到屈服强度时,二者均出现最大值;塑性变形阶段,Ks(y)随应力的增加缓慢降低,而|H(x)|则随应力的变化急剧减小。其中,参数Ks(y)在弹塑性变形阶段发生反转的现象,与董世运课题组[12]的研究结果一致。
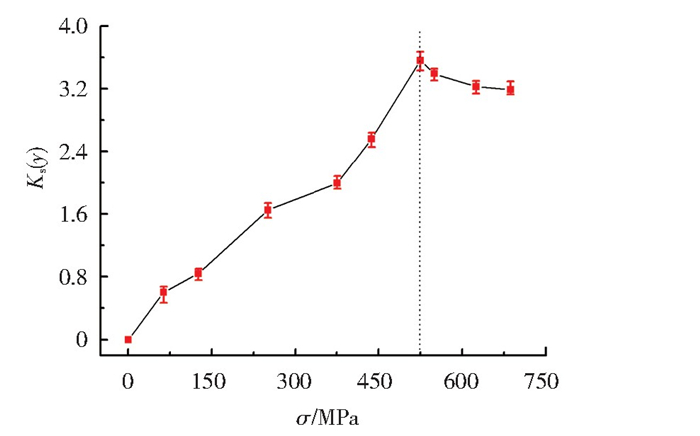
|
图 7 Ks(y)与拉应力的关系曲线 Fig.7 Relation between Ks(y) and tensile stress |
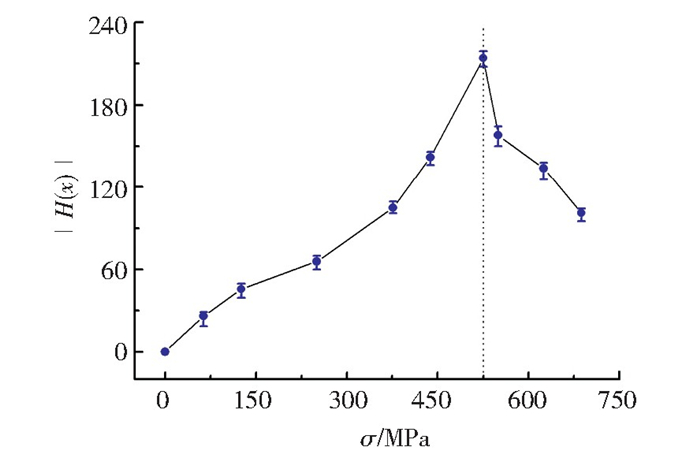
|
图 8 |H(x)|与拉应力的关系曲线 Fig.8 Relation between |H(x)| and tensile stress |
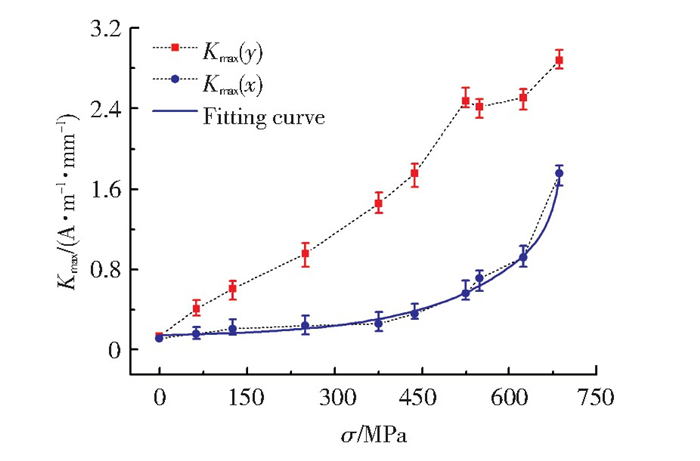
通过对磁记忆信号试验数据的分析,建立了塑性变形损伤区Lx=10~30 mm范围内磁场分量梯度最大值Kmax与应力σ的关系曲线,如图 9所示。
|
图 9 Kmax与拉应力的关系曲线 Fig.9 Relation between Kmax and tensile stress |
| ${K_{\max }} = \max (\left| {{K_i}} \right|)$ | (1) |
式中,Ki为第i个测试点的磁场分量梯度值。
由图 9可知,法向分量的Kmax(y)在弹性阶段随应力的增加而快速增大;进入塑性阶段后,Kmax(y)的增大趋势变缓;随着应力的进一步增加,试件的应力集中和变形程度加剧,Kmax(y)快速增大。这一变化趋势与文献[5]的检测结果相似。切向分量的Kmax(x)在弹性阶段随应力的增加而缓慢增大;进入塑性阶段后,Kmax(x)急剧增大。
4 分析与讨论由上述试验现象可以发现,在不同载荷作用下,磁记忆信号的变化趋势具有明显的不同,应力对试件内部磁畴和磁化矢量的变化情况影响如图 10所示。

|
图 10 应力对磁畴的影响示意图 Fig.10 Schematic diagram of the effect of stress on magnetic domains |
在弹性变形阶段,拉应力将促使铁磁材料内磁畴组织重新排列和磁化矢量转向,见图 10, 表现为试件在应力轴线方向上的均匀磁化,在地磁场作用下对外显示磁性。因此,沿轴线方向检测时,磁场强度法向分量H(y)过零点,表现为倾斜的直线,而切向分量H(x)为水平直线。
基于磁畴理论和畴壁运动建立的J-A模型认为,单轴拉应力对铁磁性材料表面磁化强度的影响,相当于对其内部的磁畴结构施加一个等效磁场[13]。弹性变形阶段材料表面的有效磁场Htotal可表示为
| ${H_{{\rm{total}}}} = H + \alpha M + {H_\sigma }$ | (2) |
式中:H为外磁场;α为磁畴耦合系数;M为材料的实际磁化强度;Hσ为应力产生的等效磁场,可表示为
| ${H_\sigma } = \frac{3}{2}\frac{\sigma }{{{\mu _0}}}\frac{{{\rm{d}}\lambda }}{{{\rm{dM}}}}({\cos ^2}\theta - v{\sin ^2}\theta )$ | (3) |
式中:σ为外应力;μ0为真空磁导率;λ为磁致伸缩系数,由于λ是M的偶函数[14], 所以当M较小时,可令λ=bM2, b为材料的相关系数;θ为外应力σ与外磁场H间的夹角;ν为泊松比。
令l2=cos2θ-νsin2θ, 将式(3)带入式(2)可得
| ${H_{{\rm{total}}}} = H + \alpha M + 3b\frac{{\sigma M}}{{{\mu _0}}}{l^2}$ | (4) |
由式(4)可知,在一定磁化强度下,外应力越大,有效场越大,其磁记忆信号也越强。因此,当拉伸载荷增加时,法向分量的斜率Ks(y)和切向分量的绝对值|H(x)|均增大。
4.2 塑性阶段分析管线钢在制造过程中,其内部难免存在杂质和缺陷。在较大的塑性变形状态下,这些缺陷区域内原有的磁畴组织将发生部分破坏和分割,形成高磁阻区,使原本均匀的磁力线发生畸变。因此,磁记忆信号的法向和切向分量在局部塑性变形区均出现了异常波动。另一方面,随着塑性变形量增大,试件内部的残余应力增加,位错密度迅速积累,阻碍了磁畴的有序化运动;同时,塑性变形卸载后的残余压缩应力,将驱使磁化矢量沿着压应力的垂直方向转动,见图 10。这些微观结构上的变化都将导致试件表面的磁场强度降低。
根据畴壁运动和位错钉扎理论,铁磁性材料发生塑性变形后,其表面的有效场应包括:外加磁场、残余应力场、塑性应变场和退磁场4部分[15]。因此,塑性变形阶段材料表面的有效磁场Htotal可表示为
| ${H_{{\rm{total}}}} = H + \alpha M + H_\sigma ^{\rm{r}} + H_\sigma ^{\rm{p}} - {D_\sigma }M$ | (5) |
在塑性阶段卸载后,将会有残余应力留存,其磁性响应特性与外加应力等同,由式(3)得残余应力对有效场的影响,
| $H_\sigma ^{\rm{r}} = 3b\frac{{{\sigma _{\rm{r}}}M}}{{{\mu _0}}}{l^2}$ | (6) |
式中σr为应力卸载后,由于晶粒的各向异性、晶粒内外的塑性变形等因素引起的残余应力。
试样经过塑性变形卸载后,材料内部留存的塑性能也会产生一定的等效场分量,而这一部分能量可以和钉扎作用相联系[16]。塑性变形产生的等效磁场为
| $H_\sigma ^{\rm{p}} = - k\left| {{\varepsilon _{\rm{p}}}} \right|$ | (7) |
式中:εp为塑性应变量;系数k=b < ∈π > /2μ0m; ∈π为畴壁上的钉扎能,与材料属性有关;m为磁畴磁矩。
残余压缩应力作用下的磁化矢量方向与外加磁场方向相反,将导致明显的退磁效应。基于这种现象,Schneider提出了应力退磁因子[17], 表示为
| ${D_\sigma } = 3\frac{{{\lambda _{\rm{s}}}{\sigma _{\rm{r}}}}}{{{M_{\rm{s}}}{B_{\rm{s}}}}}$ | (8) |
式中:λs为饱和磁滞伸缩系数;Ms为饱和磁化强度;Bs为饱和磁感应强度。
将式(6)、(7)、(8)带入式(5)中得
| $\begin{array}{l}{H_{{\rm{total}}}} = H + \alpha M + 3b\frac{{{\sigma _{\rm{r}}}M{l^2}}}{{{\mu _0}}} - \\ k\left| {{\varepsilon _{\rm{p}}}} \right| - 3\frac{{{\lambda _{\rm{s}}}{\sigma _{\rm{r}}}}}{{{M_{\rm{s}}}{B_{\rm{s}}}}}M \end{array}$ | (9) |
式(9)表明,随着塑性变形量的增加,残余应力增大,有效场逐渐减小,磁记忆信号由强变弱。因此,随着拉伸载荷的增加,法向分量斜率Ks(y)和切向分量的绝对值|H(x)|均减小。
4.3 特征参数分析由上述的力磁耦合模型分析可得,当材料由弹性变形向塑性变形转变时,磁化强度由大变小,出现反转现象。特征参数Ks(y)和|H(x|)随应力的增加先增大后减小,其变化情况直观地表现了材料的弹塑性转变过程。但|H(x)|的极值特征更加明显,随应力的变化更加显著,说明|H(x)|与变形状态之间存在较好的相关性。因此,可以利用|H(x)|的极大值,来判断试件是否进入塑性变形状态。
随着应力的增加,磁场分量梯度最大值Kmax(y)和Kmax(x)分阶段持续增大,其数值大小直接反映了试件的应力集中状态和塑性变形程度。特别是切向分量Kmax(x)在塑性阶段随应力的增加而急剧增大,表明其对应力的变化比法向分量更敏感。采用指数拟合法得到图 9中曲线Kmax(x)与应力σ的量化关系.
| ${K_{\max }}(x) = 0.164 + 0.003\exp ( - \sigma /112.248)$ | (10) |
| ${R^2} = 0.989\;54$ | (11) |
式中R为拟合相关系数。
由式(10)可以看出,在试验条件下,X80管线钢的应力状态与磁场切向分量梯度呈非线性的定量关系。这种关系在一定程度上可为X80管线钢构件塑性损伤的无损评价提供参考依据。
5 结论1) 弹性阶段磁场法向分量H(y)曲线近似为斜直线,切线分量H(x)为水平直线,随着应力的增加,H(y)的斜率和H(x)的绝对值均增大;塑性阶段,两者均减小。
2) 建立了弹性阶段的有效场力磁耦合模型,在此基础上引入塑性应变场和退磁场,建立了塑性阶段的有效场力磁耦合模型。这些模型可以解释磁信号发生反转的现象。
3) 切向分量对局部塑性变形的表征比法向分量更为敏感。以切向分量的绝对值H(x)为特征参数,其随应力变化的反转变化趋势,可作为识别弹塑性变形状态的依据。
4) 建立了切向磁场梯度最大值Kmax(x)与应力σ的量化关系,利用Kmax(x)值可以表征试件的应力集中程度。
| [1] |
梁永宽, 杨馥铭, 尹哲祺, 等. 油气管道事故统计与风险分析[J]. 油气储运, 2017, 36(4): 472-476. LIANG Yongkuan, YANG Fuming, YIN Zheqi, et al. Accident statistics and risk analysis of oil and gas pipelines[J]. Oil & Gas Storage and Transportation, 2017, 36(4): 472-476. DOI:10.6047/j.issn.1000-8241.2017.04.020 |
| [2] |
任吉林, 林俊明. 金属磁记忆检测技术[M]. 北京: 中国电力出版社, 2000: 74-75. REN Jilin, LIN Junming. Metal magnetic memory testing technology[M]. Beijing: China Electric Power Press, 2000: 74-75. |
| [3] |
DOUBOV A A. Diagnostics of equipment and constructions strength with usage of magnetic memory[J]. Inspection Diagnostics, 2001, 35(6): 19-29. |
| [4] |
DONG L H, XU B S, DONG S Y, et al. Stress dependence of the spontaneous stray field signals of ferromagnetic steel[J]. NDT and E International, 2009, 42(4): 323-327. DOI:10.1016/j.ndteint.2008.12.005 |
| [5] |
易术春, 王威, 苏三庆, 等. 利用磁记忆信号特征参数表征拉伸应力状态[J]. 振动、测试与诊断, 2017, 37(4): 667-672. YI Shuchun, WANG Wei, SU Sanqing, et al. Using the characteristic parameters of magnetic memory signal to evaluate the tensile stress state[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(4): 667-672. DOI:10.16450/j.cnki.issn.1004-6801.2017.04.005 |
| [6] |
李云飞, 韦利明, 万强. X80管线钢不同缺陷类型的磁记忆检测试验研究[J]. 材料科学与工艺, 2019, 27(1): 53-58. LI Yunfei, WEI Liming, WANG Qiang. Experimental investigation on metal magnetic memory testing of different defects of X80 pipeline steel[J]. Materials Science and Technology, 2019, 27(1): 53-58. DOI:10.11951/j.issn.1005-0299.20170299 |
| [7] |
SABLIK M J, RIOS S, LANDGRAF F J G, et al. Modeling of sharp change in magnetic hysteresis behavior of electrical steel at small plastic deformation[J]. Journal of Applied Physics, 2005, 97: 10E518-1-3. DOI:10.1063/1.1856191 |
| [8] |
WANG Z D, DENG B, YAO K. Physical model of plastic deformation on magnetization in ferromagnetic materials[J]. Journal of Applied Physics, 2011, 109(8): 083928. DOI:10.1063/1.3574923 |
| [9] |
刘清友, 罗旭, 朱海燕, 等. 基于Jiles-Atherton理论的铁磁材料塑性变形磁化模型修正[J]. 物理学报, 2017, 66(10): 107501. LIU Qingyou, LUO Xu, ZHU Haiyan, et al. Modeling plastic deformation effect on the hysteresis loops of ferromagnetic materials based on modified Jiles-Atherton model[J]. Acta Physica Sinica, 2017, 66(10): 107501. DOI:10.7498/aps.66.107501 |
| [10] |
宛德福, 马兴隆. 磁性物理学[M]. 北京: 电子工业出版社, 1999: 205-211. WAN Defu, MA Xinglong. Magnetic physics[M]. Beijing: Publishing House of Electronics Industry, 1999: 205-211. |
| [11] |
DOUBOV A A. Diagnostics of metal items and equipment by means of metal magnetic memory[C]// Proceeding of the 7th Conference on NDT and International Research Symposium. [S. l. ]: [S. n. ], 1999: 181-187.
|
| [12] |
王丹, 董世运, 徐滨士, 等. 静载拉伸45钢材料的金属磁记忆信号分析[J]. 材料工程, 2008, 8: 77-80. WANG Dan, DONG Shiyun, XU Binshi, et al. Metal magnetic memory testing signals of 45 carbon steel during static tension process[J]. Journal of Materials Engineering, 2008, 8: 77-80. |
| [13] |
JILES D C, ATHERTON D L. Theory of ferromagnetic hysteresis[J]. Journal of Magnetization and Magnetic materials, 1986, 61(1-2): 48-60. DOI:10.1016/0304-8853(86)90066-1 |
| [14] |
JILES D C. Theory of the magnetomechanical effect[J]. Journal of Physics D, 1995, 28(8): 1537-1546. DOI:10.1088/0022-3727/28/8/001 |
| [15] |
LI J W, XU M Q, LENG J C, et al. Modeling plastic deformation effect on magnetization in ferromagnetic materials[J]. Journal of Applied Physics, 2012, 111(6): 063909. DOI:10.1063/1.3695460 |
| [16] |
LENG J C, LI L, GAO Y T, et al. Modelling dependence of magnetic memory effect on plastic deformation in ferromagnetic materials[J]. Materials Science and Technology, 2014, 30(1): 81-85. DOI:10.1179/1743284713Y.0000000307 |
| [17] |
SCHNEIDER C S, CANNELL P Y. Magnetoelasticity for large stresses[J]. IEEE Transactions on Magnetics, 1992, 28(5): 2626-2631. DOI:10.1109/20.179578 |
 2021, Vol. 29
2021, Vol. 29


