NiCrMo系低合金钢SA508Gr.4N相比于目前广泛应用于核岛压力容器用MnMoNi系低合金钢SA508Gr.3,由于增加了Ni和Cr元素含量,使其具有更高强度和低温韧性,是核岛压力容器大型化、一体化发展的首选材料之一,国内通用牌号为R17Cr1Ni3Mo[1-3]。大锻件的成型是长时间,多火次,多道次的过程,由于大锻件厚截面、大体积的特点,容易造成心部达到所需温度时,表层已长时间处于高温状态,导致截面方向晶粒尺寸差异较大,因此,每一火次前的加热工艺对锻件锻造前的初始晶粒度及均匀化程度具有重要影响[4-6]。国内外许多学者已对晶粒长大机制和数学模型的建立进行了大量的研究。研究表明:晶粒长大过程实质上是晶界迁移的过程[7-9],研究者还通过对实验数据的分析建立了包含保温温度和保温时间的晶粒长大模型,如Beck模型[10-11]、Arrhenius模型[12]、Sellar模型[13]、Sellar-Anelli模型[14]等。此外,钢中第二相颗粒在晶界处析出,对晶粒长大产生较强的钉扎作用,阻碍晶界迁移,使得奥氏体粗化温度升高[15-16]。
目前,针对SA508Gr.4N钢奥氏体晶粒长大行为研究甚少。因此,本文将较为系统地研究SA508Gr.4N钢的奥氏体晶粒与保温温度和加热时间的关系,采用最小二乘法非线性拟合的方法,构建SA508Gr.4N钢的奥氏体晶粒长大模型,并验证模型的准确性,以期为SA508Gr.4N钢大锻件锻前加热工艺的制定提供参考。此外,还将通过高温激光共聚焦显微镜研究SA508Gr.4N钢的晶粒长大机制。
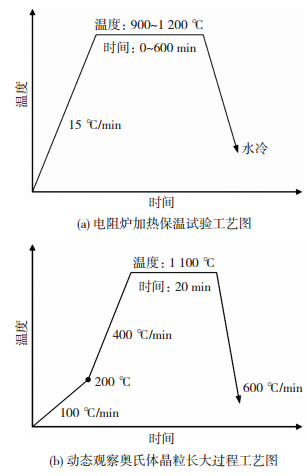
1 试验试验用SA508Gr.4N钢的化学成分如表 1所示。试验钢为Φ2 000 mm×700 mm饼型锻件心部解剖料。将试样线切割成15 mm×15 mm×15 mm的块状料,采用精密自动温控的箱式电阻炉进行加热保温实验,具体过程如下。将试样以15 ℃/min的升温速度加热至900、950、1 000、1 050、1 100、1 150和1 200 ℃,分别保温0、30、60、120、240、360、480和600 min,出炉水冷,工艺如图 1(a)所示,其中,保温时间不包括试样从室温升高至指定温度的时间,试样从室温升至指定温度时即为保温0 min。试样经砂纸研磨、机械抛光后,采用过饱和苦味酸溶液与洗涤剂10 ∶1的混合溶液,侵蚀大约10 min,浸蚀后的试样在Zeiss 40MAT数字金相显微镜上观察其显微组织。
| 表 1 SA508Gr.4N钢化学成分(质量分数/%) Table 1 Chemical composition of SA508Gr.4N steel (wt.%) |
|
图 1 实验工艺图 Fig.1 Test process diagram: (a)heat insulation test process diagram of resistance furnace; (b) process diagram for dynamic observation of austenite grain growth process |
为动态观察SA508Gr.4N钢奥氏体晶粒的长大过程,将试样加工成Φ6 mm×3 mm的圆柱,将试样上表面经砂纸研磨、机械抛光后放入氧化铝坩埚中,放置在VL2000DX-SVF17SP型高温激光共聚焦显微镜内,加热前将设备抽至10-2 Pa的真空状态并通入保护气体(氩气),以防止试样表面氧化。将试样先以100 ℃/min的速度升温到200 ℃,然后以400 ℃/min的速度升温到1 100 ℃保温20 min,而后以600 ℃/min的速度降温至室温,如图 1(b)所示。实验过程中以5帧/s的速度进行动态观察。所有试样均采用ASTM E112-10标准对晶粒度进行测定。
2 结果与分析 2.1 保温温度对奥氏体晶粒尺寸的影响图 2为保温60 min时,不同保温温度下奥氏体晶粒的微观组织,可以看出,随着温度的增加晶粒形状由不规则,晶界弯曲的状态(900 ℃)转变为晶粒形状近似六边形,晶界平直的状态(≥1 050 ℃)。随着温度的升高,奥氏体平均晶粒尺寸(D)逐渐增加。当温度不高于1 000 ℃时,晶粒尺寸变化较小,晶粒尺寸由900 ℃时的33.87 μm,增加到1 000 ℃的65.23 μm,如图 2(a)~(c)所示;温度高于1 000 ℃时,晶粒尺寸迅速增大,由1 050 ℃时的125.51 μm增加到1 200 ℃的890.12 μm,即晶粒严重粗化,如图 2(d)~(f)所示。

|
图 2 保温60 min不同保温温度下奥氏体晶粒微观形貌 Fig.2 Microscopic morphology of austenite grains at different holding temperatures for 60 min: (a)900 ℃; (b)950 ℃; (c)1 000 ℃; (d)1 050 ℃; (e)1 100 ℃; (f)1 200 ℃ |
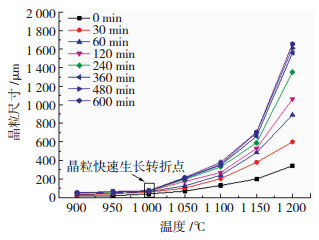
图 3为不同保温时间下奥氏体晶粒平均尺寸随保温温度的变化规律。在相同保温时间下,保温温度越高,奥氏体晶粒尺寸越大。当加热温度不高于1 000 ℃时,奥氏体晶粒尺寸增加缓慢,曲线呈扁平状;当加热温度高于1 000 ℃时,奥氏体晶粒尺寸迅速增大,且变化趋势逐渐近似于指数函数状。从图 3中的转折点位置能够看到,当保温时间为240 min,保温温度为900、950、1 000、1 050、1 100、1 150、1 200 ℃时,平均晶粒尺寸分别为46.02、60.21、72.89、194.83、330.43、590.17和1 353.24 μm,表明此实验钢在1 000 ℃以下具有较强的抗粗化能力。就锻件控制晶粒尺寸的角度而言,锻前保温温度最高不应超过1 000 ℃。
|
图 3 奥氏体晶粒尺寸随保温温度的变化规律 Fig.3 Variation of austenite grain size with holding temperature |
从动力学和热力学角度综合分析,奥氏体晶粒的生长是一种热激活、扩散与界面反应控制的物理冶金过程,主要表现为晶界的迁移[17-18]。正常晶粒长大速度与晶界的迁移速率和驱动力有关,其表达式为
| $ v = MF $ | (1) |
| $ M = {M_0}{\rm{ex}}{{\rm{p}}^{ - \frac{{{Q_1}}}{{{k_{\rm{B}}}T}}}} $ | (2) |
式中:v为晶粒长大速度;M为晶界迁移速率;M0为常数;kB为玻尔兹曼常数;Q1为热激活能;T为温度;F为驱动力, 相当于晶界相对位移的自由能变化。
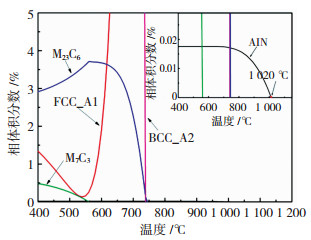
从式(1)和(2)可以看出,正常晶粒长大的速度主要受温度的影响,温度越高晶粒长大速度越快。影响晶粒长大的另一因素为钢中未溶的第二相颗粒,如钢中添加Al元素,主要作用是形成细小弥散的AlN钉扎晶界[19-20]。钢中的Al原子尺寸大于Fe原子,在应力作用下,Al原子易在晶界处偏聚,形成AlN颗粒,减缓了晶界的迁移速度。为了进一步研究第二相AlN颗粒对奥氏体晶粒长大的影响,通过Thermo-Calc软件计算此实验钢的平衡相图,如图 4所示,可以发现随着温度的升高,第二相AlN颗粒含量(质量分数)逐渐下降,至1 020 ℃全部溶解,Al原子以固溶的形式全部溶解到基体中。
|
图 4 实验钢热动力学计算图 Fig.4 Thermodynamic calculation diagram of experimental steel |
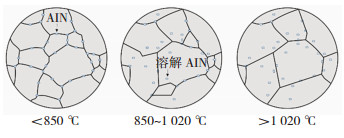
图 5为奥氏体晶粒粗化和混晶组织的发展过程。从850到1 020 ℃,AlN颗粒开始溶解,失去原始的钉扎作用,这意味着溶解的AlN不再阻碍该区域奥氏体晶界的运动。从图 2和图 4可知,900 ℃时,溶解的33.7%的AlN颗粒失去了对该区域的奥氏体晶界运动的阻碍作用,使得部分晶粒异常长大,造成混晶现象;超过1 020 ℃时,AlN颗粒全部溶解,奥氏体晶界生长不再有阻碍作用,奥氏体晶粒生长只受加热温度的影响,混晶组织转变为均匀的晶粒组织。1 200 ℃保温过程中晶粒急剧长大,主要是由于钢中AlN颗粒被完全溶解,且温度过高,导致晶界迁移速率加大,使得SA508Gr.4N钢出现过热现象。
|
图 5 奥氏体粗化和混晶示意图 Fig.5 Austenite coarsening and mixed grain diagram |
图 6为保温温度为1 050 ℃时不同保温时间下的奥氏体晶粒形貌。由图 6可知,随着保温时间的增加,奥氏体晶粒尺寸先迅速增大,而后逐渐趋势稳定。奥氏体晶粒尺寸由保温时间为0 min的69.35 μm增加到保温时间为240 min的194.83 μm,当保温时间为480 min时,奥氏体晶粒尺寸为207.06 μm,相较于保温时间为240 min时,晶粒尺寸仅增加了16.23 μm,表现出随保温时间延长奥氏体晶粒尺寸增幅逐渐下降的趋势。

|
图 6 温度1 050 ℃不同保温时间下奥氏体晶粒微观形貌 Fig.6 Microstructure of austenite grain at 1 050 ℃ for different holding time: (a)0 min; (b)30 min; (c)60 min; (d)120 min; (e)240 min; (f)480 min |
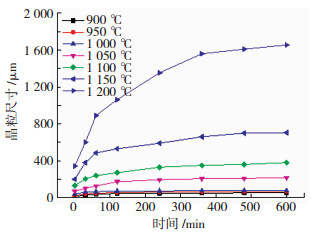
图 7为不同保温温度下奥氏体晶粒平均尺寸随保温时间的变化规律。由图 7可知,在相同保温温度下,保温时间越长,奥氏体晶粒尺寸越大,且随着保温时间的增加,晶粒的生长速度逐渐趋缓;在温度不高于1 000 ℃时,随保温温度和保温时间的延长,晶粒尺寸的增幅不明显;但当保温温度为1 050~1 200 ℃时,随着保温时间的延长,奥氏体晶粒尺寸呈现出快速增长的变化趋势,尤其是在保温温度为1 200 ℃情况下。综上所述,为了控制锻件的晶粒尺寸,应采用以心部加热到所需温度后直接出炉,进行锻造即可。
|
图 7 奥氏体晶粒尺寸随保温时间的变化规律 Fig.7 Variation of austenite grain size with holding time |
研究表明,保温温度越高,原子的迁移能力越强,晶粒生长越快,奥氏体晶粒尺寸越大[10, 15, 18]。此外,当保温温度低于钢中第二相粒子(AlN、Ti(CN)、Nb(CN)等)的溶解温度时,第二相粒子对晶界的迁移起到钉扎作用,阻碍奥氏体晶粒的长大[19-21]。
为了进一步研究SA508Gr.4N钢晶粒演变规律,采用高温激光共聚焦显微镜对晶粒生长过程进行动态观察。晶粒长大的实质是晶界的迁移过程,迁移方式主要有以下几种。
1) 角隅的迁移、合并及消失过程。图 8中A区域中黑色箭头所指的角隅沿着红色箭头方向迁移,角隅的移动激发临近一条晶界的迁移,如图 8(b)所示。可能原因是由于晶粒内部第二相钉扎力较弱,角隅沿着晶界向晶粒内部或晶界另一端开始生长,伴随着临近晶界也向晶粒内部或晶界另一端移动、缩小,直至达到一个较为稳定的状态,如图 8(d)所示。

|
图 8 奥氏体晶界迁移动过程 Fig.8 Process of austenite grain boundary migration |
2) 如图 8中区域B所示,几个角隅同时向着一个晶粒内部分批协同式的移动,直至小晶粒被周围大晶粒吞并,形成图 8(d)中B区域的大晶粒。
3) 图 8中C区域中两个比较稳定的大晶粒之间的弯曲晶界沿着曲率中心方向(箭头)移动,出现平直化现象,这是由于弯曲晶界的界面能较高,平直晶界的界面能较低,必然会发生这种向低界面能晶界迁移的现象。
3 晶粒长大动力学模型上述研究表明,保温温度和保温时间对奥氏体晶粒尺寸的影响是呈正相关的关系。当加热温度为1 020 ℃时,由于钢中阻碍晶界运动的AlN颗粒完全溶解,导致晶粒尺寸急剧增加,因此,在建立奥氏体晶粒长大模型时应以1 000 ℃为分界点,建立900~1 020 ℃和1 020~1 200 ℃两阶段晶粒长大模型。目前考虑晶粒生长过程与保温温度和保温时间关系的模型有Sellars(式(3))、Anelli[22](式(4))和Sellars-Anelli(式(5))3种模型。
| $ {D^n} = D_0^n + At{\rm{exp}}\left( { - \frac{Q}{{RT}}} \right) $ | (3) |
| $ D = B{t^m}{\rm{exp}}\left( { - \frac{Q}{{RT}}} \right) $ | (4) |
| $ {D^n} = D_0^n + A{t^m}{\rm{exp}}\left( { - \frac{Q}{{RT}}} \right) $ | (5) |
式中:D为奥氏体晶粒尺寸,μm;D0为初始奥氏体晶粒尺寸,μm;T为保温温度,℃;t为保温时间,s;Q为晶粒长大激活能,J/mol;R为摩尔气体常数,8.314 J/(mol·K);A,B,n,m均为常数。
相较于式(4),式(3)考虑了初始晶粒尺寸的影响,但并未引用时间指数,而式(5)相较于前两者既考虑了初始晶粒尺寸的影响,又考虑了时间指数的影响,对奥氏体晶粒尺寸的预测更加合理。
基于实验数据,采用最小二乘法对Sellars模型(式(3))和Sellars-Anelli模型(式(5))进行非线性拟合,拟合后的公式分别为式(6)和(7)。
| $ \left\{ {\begin{array}{*{20}{c}} {{D^{4.13}} = D_0^{4.13} + 2.94 \times {{10}^6} \times t \times {\rm{exp}}\left( { - \frac{{12\;525.62}}{{RT}}} \right)}\\ {900\;{\rm{℃}} \le T \le 1\;020\;{\rm{℃}}}\\ {{D^{1.32}} = D_0^{1.32} + 1.07 \times {{10}^{10}} \times t \times {\rm{exp}}\left( { - \frac{{29\;108.93}}{{RT}}} \right)}\\ {1\;020\;{\rm{℃}} < T \le 1\;200\;{\rm{℃}}} \end{array}} \right. $ | (6) |
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{D^{2.74}} = D_0^{2.74} + 5.29 \times {{10}^8} \times {t^{0.36}} \times {\rm{exp}}\left( { - \frac{{127\;355.94}}{{RT}}} \right)}\\ {900\;℃ \le T \le 1\;020\;℃}\\ {{D^{0.57}} = D_0^{0.57} + 3.89 \times {{10}^6} \times {t^{0.37}} \times {\rm{exp}}\left( { - \frac{{186\;539.01}}{{RT}}} \right)}\\ {1\;020\;℃ < T \le 1\;200\;℃} \end{array}} \right.\\ \end{array} $ | (7) |
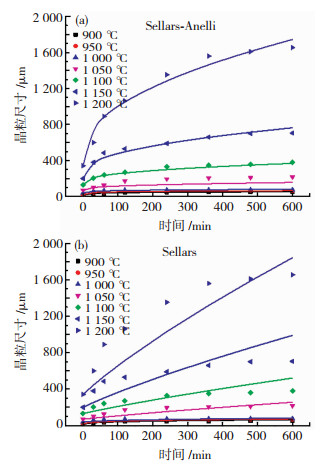
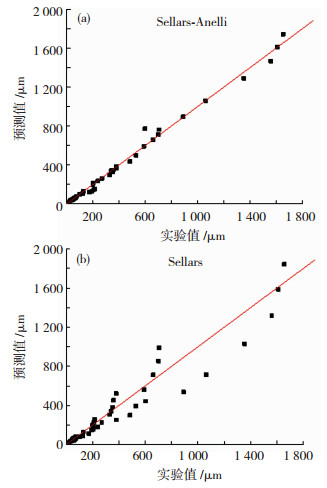
为了验证建立的SA508Gr.4N钢奥氏体晶粒长大模型的准确性,将不同保温工艺条件下的奥氏体晶粒尺寸的实验值和预测值作比较,如图 9所示,图中实线为预测值,散点为实验值。由图 9可知,采用Sellars-Anelli模型建立奥氏体晶粒长大模型,可更为准确地描述SA508Gr.4N钢在不同保温温度和时间下的奥氏体晶粒长大行为。同时,采用统计学评价指标(决定系数(R2)和平均绝对百分比误差(SMAPE))来评价模型的准确性,如式(8)和(9)所示。由式(6)和式(7)所建立的奥氏体晶粒长大模型的预测值与实验值的相关性如图 10所示,R2分别为0.99和0.92,SMAPE分别为6.75%和15.90%,由此可知,Sellars-Anelli模型建立的奥氏体晶粒长大模型更为准确。
| $ {R^2} = \frac{{\sum {{\left( {y - \bar x} \right)}^2}}}{{\sum {{\left( {x - \bar x} \right)}^2}}} $ | (8) |
| $ {\rm{SMAPE}} = \frac{1}{{{n_1}}} \times \sum \frac{{\left| {{\rm{ }}y - x} \right|}}{{\frac{{\left| {{\rm{ }}y{\rm{ }}} \right| + \left| {{\rm{ }}x{\rm{ }}} \right|}}{2}}} \times 100\% $ | (9) |
|
图 9 模型预测值和实验值对比 Fig.9 Comparison of predicted and experimental values of the model |
|
图 10 模型预测值和实验值相关性 Fig.10 Correlation between predicted and experimental values of the model |
式中:x,y分别是实验值和预测值;x是实验值的平均值;n1是此统计计算中使用的数据总数。
4 结论1) 在保温过程中,SA508Gr.4N钢的晶粒长大速度与保温温度、保温时间和钢中第二相密切相关。温度低于1 000 ℃时,由于钢中AlN的钉扎作用使得部分晶粒长大缓慢,出现混晶现象;温度高于1 000 ℃时,钢中AlN全部溶解,晶粒长大速度急剧增加;当保温温度一定时,随着保温时间的增加,奥氏体晶粒尺寸增幅逐渐下降;就晶粒尺寸而言,大锻件锻前保温温度不应超过1 000 ℃,保温时间为心部到温即可出炉。
2) SA508Gr.4N钢的奥氏体晶粒长大实质为晶界迁移过程,具体表现为:角隅的迁移、合并及消失过程和弯曲晶界平直化过程。
3) 采用Sellars-Anelli模型建立了SA508Gr.4N钢在不同保温温度和时间下的奥氏体晶粒长大模型,模型的相关系数较高,模型的计算值与实测值吻合较好。
| [1] |
YANG Zhiqiang, LIU Zhengdong, HE Xikou, et al. Effect of microstructure on the impact toughness and temper embrittlement of SA508Gr.4N steel for advanced pressure vessel materials[J]. Scientific Reports, 2018, 8(1): 207-218. DOI:10.1038/s41598-017-18434-3 |
| [2] |
李云良, 张汉谦, 彭碧草, 等. 核电压力容器用钢的发展及研究现状[J]. 压力容器, 2010(5): 36-43. LI Yunliang, ZHANG Hanqian, PENG Bicao, et al. Development and recent research of nuclear reactor pressure vessel steels[J]. Pressure Vessel Technology, 2010(5): 36-43. DOI:10.3969/j.issn.1001-4837.2010.05.008 |
| [3] |
LIU Ning, LIU Zhengdong, HE Xikou, et al. Structure inheritance removing of SA508Gr.4N steel for nuclear reactor pressure vessels[J]. Journal of Iron & Steel Research, 2017, 29(5): 402-410. DOI:10.13228/j.boyuan.issn1001-0963.20170015 |
| [4] |
董定乾. 核电用钢SA508-3热锻全流程晶粒演变数学模型及其在封头成形中的应用[D]. 上海: 上海交通大学, 2016. DONG Dingqian. Mathematical model of grain evolution for nuclear power SA508-3 steel during hot forging process and its application in the development of heavy pressure vessel head forming[D]. Shanghai: Shanghai Jiao Tong University, 2016. |
| [5] |
秦尚武, 党淑娥, 侯微, 等. 多次降梯加热对30Cr2Ni4MoV钢晶粒大小的影响[J]. 大型铸锻件, 2017(1): 15-20. QIN Shangwu, DANG Shu'e, HOU Wei, et al. Effect of multiple descending heating on grain size of 30Cr2Ni4MoV steel[J]. Heavy Castings and Forgings, 2017(1): 15-20. |
| [6] |
赵石岩, 李光磊, 郭宝峰, 等. 大型轴类锻件锻前加热的热透时间研究[J]. 金属热处理, 2012, 37(5): 118-121. ZHAO Shiyan, LI Guanglei, GUO Baofeng, et al. Investigation on through heating time of large shaft-forgings in pre-forging heating process[J]. Heat Treatment of Metals, 2012, 37(5): 118-121. |
| [7] |
胡海江, 徐光, 张玉龙, 等. 先进贝氏体钢奥氏体晶粒长大行为的动态观察[J]. 材料热处理学报, 2014, 35(1): 83-87. HU Haijiang, XU Guang, ZHANG Yulong, et al. Dynamic observation of austenite grain growth behavior of an advanced bainite steel[J]. Transactions of Materials and Heat Treatment, 2014, 35(1): 83-87. |
| [8] |
CHEN R C, HONG C, LI J J, et al. Austenite grain growth and grain size distribution in isothermal heat-treatment of 300M steel[J]. Procedia Engineering, 2017, 207: 663-668. DOI:10.1016/j.proeng.2017.10.1038 |
| [9] |
胡德林, 刘智恩. 奥氏体晶界迁移过程的研究[J]. 金属学报, 1986, 22(4): 56-152. HU Delin, LIU Zhien. Study on austenite grain boundary migration process[J]. Acta Metallurgica Sinica, 1986, 22(4): 56-152. |
| [10] |
龚虎, 郭桢, 刘建生. 锻态12%Cr超超临界转子钢的奥氏体晶粒长大行为[J]. 金属热处理, 2017, 42(10): 215-219. GONG Hu, GUO Zhen, LIU Jiansheng. Growth behavior of austenite grain of forged 12%Cr ultra-supercritical rotor steel[J]. Heat Treatment of Metals, 2017, 42(10): 215-219. |
| [11] |
陈磊, 闫洪, 郑志强, 等. 盾构刀具用5Cr5MoSiV1钢的奥氏体晶粒长大规律研究[J]. 材料科学与工艺, 2012, 20(4): 140-143. CHEN Lei, YAN Hong, ZHENG Zhiqiang, et al. Study on austenite grain growth behavior of 5Cr5MoSiV1 steel for shield tools[J]. Materials Science and Technology, 2012, 20(4): 140-143. |
| [12] |
温余远, 鲁世强, 刘俊伟, 等. 基于Matlab的300M钢奥氏体晶粒的长大规律[J]. 材料热处理学报, 2012, 33(9): 75-79. WEN Yuyuan, LU Shiqiang, LIU Junwei, et al. Austenite grain growth behavior of 300 M alloy steel based on Matlab[J]. Transactions of Materials and Heat Treatment, 2012, 33(9): 75-79. |
| [13] |
梁博. 结构钢加热过程中奥氏体晶粒长大模型及应用[J]. 热加工工艺, 2013, 42(22): 80-82. LIANG Bo. Austenite grain growth model and application in heating process of structural steel[J]. Hot Working Technology, 2013, 42(22): 80-82. |
| [14] |
DONG Dingqian, CHEN Fei, CUI Zhenshan. Modeling of austenite grain growth during austenitization in a low alloy steel[J]. Journal of Materials Engineering and Performance, 2016, 25(1): 152-164. DOI:10.1007/s11665-015-1810-9 |
| [15] |
汪杨鑫, 赵秀明, 毛向阳, 等. SCr420H钢奥氏体晶粒长大动力学[J]. 钢铁, 2018, 53(7): 86-90, 110. WANG Yangxin, ZHAO Xiuming, MAO Xiangyang, et al. Kinetics of austenite grain growth in SCr420H steel[J]. Iron and Steel, 2018, 53(7): 86-90, 110. |
| [16] |
ZHANG Yan, LI Xiaohua, LIU Yongchang, et al. Study of the kinetics of austenite grain growth by dynamic Ti-rich and Nb-rich carbonitride dissolution in HSLA steel: in-situ observation and modelingl[J]. Materials Characterization, 2020, 169: 110612. DOI:10.1016/j.matchar.2020.110612 |
| [17] |
GLEITER H. Theory of grain boundary migration rate[J]. Acta Metallurgica, 1969, 17(7): 853-862. DOI:10.1016/0001-6160(69)90105-9 |
| [18] |
CHEN K, HAN J, SROLOVITZ D J. On the temperature dependence of grain boundary mobility[J]. Acta Materialia, 2020, 194: 412-421. DOI:10.1016/j.actamat.2020.04.057 |
| [19] |
POUS-ROMERO H, LONARDELLI I, COGSWELL D, et al. Austenite grain growth in a nuclear pressure vessel steel[J]. Materials Science & Engineering A, 2013, 567: 72-79. DOI:10.1016/j.msea.2013.01.005 |
| [20] |
LIU Ziyi, BAO Yanping, WANG Min, et al. Austenite grain growth of medium-carbon alloy steel with aluminum additions during heating process[J]. International Journal of Minerals Metallurgy & Materials, 2019, 26(3): 282-290. DOI:10.1007/s12613-019-1736-6 |
| [21] |
王猛, 王晓晨, 程四华, 等. 含Nb高碳钢的奥氏体晶粒长大模型[J]. 材料热处理学报, 2016, 37(4): 243-248. WANG Meng, WANG Xiaochen, CHENG Sihua, et al. Grain growth model of austenite in a Nb-microalloyed high carbon steel[J]. Transactions of Materials and Heat Treatment, 2016, 37(4): 243-248. |
| [22] |
ANELLI E. Application of mathematical modelling to hot rolling and controlled cooling of wire rods and bars[J]. ISIJ International, 1992, 32(3): 440-449. DOI:10.2355/isijinternational.32.440 |
 2021, Vol. 29
2021, Vol. 29


