随着“国六”标准的公布,汽车行业面临着加速转型,氢燃料电池汽车备受关注。供氢系统是氢燃料电池汽车的核心系统之一,而储氢气瓶则是供氢系统的主要部件。
目前,储氢气瓶主要是铝内胆碳纤维缠绕气瓶,即Ⅲ型气瓶。各国标准对Ⅲ型气瓶的设计流程和参考公式无明确规定,主要采用有限元分析与破坏性试验相结合的方式来验证设计及产品质量。缐永兴[1]验证了环/螺交替缠绕能更好发挥纤维强度。林松等人[2]研究了聚酰亚胺纤维在复合材料气瓶上的应用。付敏等人[3]用数值模拟方法分析金属内衬的屈曲模态,与试验结果相符。李地红等人[4]开发了纤维缠绕过程模拟软件。HARADA等人[5]提出考虑纤维体积分数影响的气瓶爆破压力预测方法。ZU等人[6]基于非测地线缠绕设计缠绕参数,并通过有限元分析了爆破压力。ZHANG等人[7]提出了预测储氢瓶封头厚度和设计内衬气压的方法。FERNANDES等人[8]用有限元法设计了船用自给式呼吸器气瓶并测试合格。MOHAMMAD等人[9]基于遗传算法优化了气瓶的屈曲载荷和重量并验证。CAMARA等人[10]类比单向增强板与纤维缠绕压力容器的失效并确定强度和失效概率。LIU等人[11]用迭代算法优化缠绕角和缠绕张力,提高容器承载能力。
现有的研究主要关注对具体气瓶的性能预测及优化,而对气瓶铺层的初步设计关注较少。目前,气瓶设计主要依赖有限元方法的多次试算,效率不高。因此,有必要研究既便捷又能满足要求的铺层设计新方法。
本文对工作压力p=35 MPa的Ⅲ型气瓶铺层及自紧力设计、性能验证展开研究。主要参考标准为GB/T 35544-2017[12]。基于该标准对气瓶疲劳性能的要求,利用网格理论和铝合金S-N曲线设计铺层厚度,构建有限元模型,求解自紧力的合理取值,分析自紧效果及气瓶的综合性能,结合试验数据预测气瓶的爆破强度、破坏形式。
通常金属材料的疲劳极限是拉伸强度的40%~50%,碳纤维复合材料为拉伸强度的70%~90%[13]。缠绕层的抗疲劳能力远优于内胆,因此铺层设计只考虑铝内胆的疲劳。
1 气瓶结构与铺层设计 1.1 内胆结构气瓶的内胆结构见图 1。内胆总长1 820 mm,内径347 mm,筒身壁厚6 mm。

|
图 1 气瓶内胆结构(单位:mm) Fig.1 Cylinder structure |
气瓶内胆材料为6061-T6铝合金,弹性模量E=71 GPa,泊松比υ=0.33,屈服强度RP0.2为318 MPa,断裂延伸率14%,符合GB/T 35544标准6.1.4.2小项的要求。
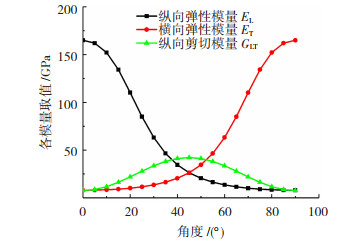
碳纤维为T700S,断裂延伸率A=2%,制得的树脂基复合材料弹性常数见表 1。依据层合板理论[14]可得螺旋缠绕层弹性常数与角度的关系如图 2所示。
| 表 1 T700S复合材料正轴工程弹性常数 Table 1 Engineering elastic constants of T700S composite |
|
图 2 螺旋缠绕层弹性常数与铺层角度关系 Fig.2 Spiral elastic constant under lay angle |
经典网格理论[15]给出了网络分析公式:
| $ {\alpha _0} = \arcsin (\frac{r}{R}) $ | (1) |
| $ {\lambda _{{\rm{ \mathsf{ θ} }}\alpha }} = (\eta + 1){\cos ^2}{\alpha _0} - 1 $ | (2) |
| $ {t_{{\rm{f \mathsf{ θ} }}}} \ge \frac{{R \bullet {p_{\rm{B}}}}}{{2{R_{\rm{m}}}}}(2 - {\tan ^2}{\alpha _0}) $ | (3) |
| $ {t_{{\rm{f \mathsf{ α} }}}} \ge \frac{{{t_{{\rm{f \mathsf{ θ} }}}}}}{{{\lambda _{{\rm{ \mathsf{ θ} \mathsf{ α} }}}}}} $ | (4) |
式中: r为瓶口半径;R为内胆筒身段半径;λθα为环螺厚度比;η为内力比,均匀内压作用下η=2;tfa为螺旋层厚度;tfθ为环向层厚度;pB为爆破压力;α0为螺旋缠绕角;Rm为碳纤维复合材料许用强度。
基于给定的内胆尺寸,一般通过上式计算满足爆破强度要求的最小铺层厚度。但该方法未考虑GB/T 35544标准对气瓶疲劳性能的要求,由于疲劳是更为危险的失效形式,故上述最小厚度低于合格气瓶所需的铺层厚度,不能适应铺层设计的需要。
为此,需要研究基于疲劳性能而非爆破强度的设计铺层厚度的方法。将式(3)中的爆破压力pB=2.25 p改为疲劳试验压力pf=1.25 p,许用强度Rm相应改为疲劳载荷下的复合材料应力σf,即为式(5)。只需获得σf,即可计算满足疲劳性能要求的环向铺层最小厚度。
| $ {t_{{\rm{f \mathsf{ θ} }}}} \ge \frac{1}{2}R(2 - {\tan ^2}{\alpha _0}) \bullet \frac{{{p_{\rm{f}}}}}{{{\sigma _{\rm{f}}}}} $ | (5) |
Ⅲ型气瓶必须经过自紧,原理如图 3所示。该过程通过施加内压使铝内胆产生塑性变形,从而使零压力下铝内胆承受压应力、碳纤维承受拉应力。自紧增大了铝合金的弹性工作区域,有利于提高疲劳性能,也增加了复合材料分担的载荷,有利于充分利用碳纤维的力学性能。

|
图 3 气瓶自紧原理 Fig.3 Autofrettage principle |
通常自紧力>1.5倍工作压力,因此在后续的疲劳压力循环中铝合金和碳纤维复合材料均为弹性状态,应力-应变为线性关系。铝合金与复合材料可视作薄壳,忽略沿厚度方向的压缩应变。又由于外层模量高,内层模量低,承受内压时铝合金的变形将受到复合材料的限制,铝合金应变与复合材料相等。由铝合金环向应变可得σf,该应变通过铝合金环向应力计算。
自紧力过高会使卸载后内胆因复合材料收缩的压力而失稳。根据DOT-CFFC标准[16],自紧后气瓶内胆的残余等效应力应为屈服强度的60%~95%。此时内胆环向和轴向受压,在数值上等效应力略小于环向,因此可将卸载状态对应的内胆环向应力近似为等效应力。该处理将导致式(5)所得铺层厚度偏大,但符合压力容器保守设计原则,在一定范围内可以接受。
疲劳载荷为1.25倍工作压力时对应的环向应力可以根据铝的S-N曲线计算。
1.3.3 铝合金S-N曲线YAHR[17]基于疲劳试验总结了6061-T6合金的S-N曲线,由式(6)得到
| $ S = \frac{{14479}}{{\sqrt N }} + 96.5 $ | (6) |
式中:N为应力循环次数;S为名义应力,应变振幅与弹性模量之积,单位MPa。
依据GB/T 35544标准,公称压力为35 MPa的气瓶,设计循环次数Nd为11 000次。由式(6)可得N=11 000,S=235 MPa。若在疲劳载荷下,铝内胆的名义应力低于S,可认为气瓶的疲劳寿命满足对应的循环次数N。
1.3.4 铺层厚度计算基于上述理论和公式计算铺层参数。由式(1)可得测地线缠绕角为14.18°,考虑扩孔的影响,实际取15°;由式(2)计算得到环螺厚度比λθα=1.8。设计疲劳寿命N=11 000,则S=235 MPa (此时内胆环向受拉);设自紧力卸载后内胆的残余等效应力为屈服强度的80%(此时内胆环向受压),则疲劳压力循环下铝内胆的弹性应变区间长度为
| $ \varepsilon = \frac{{[S - ( - 0.8{R_{{\rm{p0}}{\rm{.2}}}})]}}{E} = 6.88 \times {10^{ - 3}} $ | (7) |
依据1.3.2,上式0.8Rp0.2为环向应力的近似。
碳纤维复合材料的最大应力为
| $ {\sigma _{\rm{f}}} = \varepsilon {E_{\rm{L}}}{\rm{ = }}1136\;{\rm{MPa}} $ | (8) |
带入式(4)和(5),可得环向层厚为6.4 mm,螺旋层厚为3.6 mm。
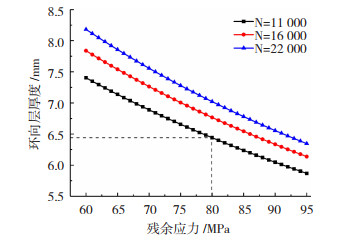
按上述过程可计算不同设计疲劳寿命和内胆残余应力条件所需的环向缠绕层最小厚度,如图 4所示(缠绕角均为15°),横轴表示残余应力相当于铝合金屈服强度的比例。由图 4可得在不同的设计要求下环向缠绕层的最小厚度值。
|
图 4 不同设计条件下的环向层厚度 Fig.4 Circumferential layer thickness under different design conditions |
采用ANSYS软件分析。由于气瓶结构及承载的对称性,可以简化为平面模型。网格单元为plane183;表征铝内胆与复合材料界面的接触单元为targe169和conta172。筒身复合材料单元按环/螺交替缠绕设置。
内胆为理想非线性模型,理由是:1)气瓶大部分载荷被复合材料承担,内胆非线性对结果的影响有限;2)自紧后,在疲劳载荷范围内铝合金为弹性状态,不受非线性的影响;3)在高压爆破中,理想非线性相当于令复合材料承担更多载荷,预期爆破压力将偏低,结果倾向保守,可以接受。
本模型可计算不同载荷顺序的气瓶应力-应变分布情况。
2.2 载荷与计算流程压力载荷作用在铝内胆内壁。为计算合理的自紧力取值,设置载荷流程如表 2所示,循环压力的上下限按照GB/T 35544标准6.2.6.1小项的规定选取。载荷步1表示自紧力值,当其为43.75 MPa时,气瓶不自紧。载荷步2为GB/T 35544标准规定的疲劳循环压力下限,载荷步3为压力上限。随着自紧力的变化,自紧效果不同,载荷步2、3的铝内胆应力场也随之变化。依据前述设计准则,对比数据得出自紧力的合理取值。
| 表 2 自紧力求解流程 Table 2 Autofrettagepressure solving process |
自紧后铝内胆在循环压力上限、下限时的等效应力分布如图 5所示,可知看到,最大等效应力出现在筒身。

|
图 5 内胆等效应力 Fig.5 Von mises stress of liner: (a) load pL=43.75 MPa; (b) load pL=1 MPa |
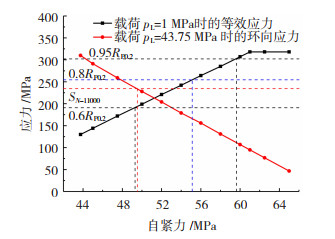
不同的自紧力取值下,铝内胆在压力循环中的等效应力、环向应力最大值曲线如图 6所示。由图可知:随自紧力增加,卸载时的应力增加,承载时的应力下降,合适的自紧力有利于提高气瓶的疲劳性能。
|
图 6 内胆应力-自紧力关系 Fig.6 Stress under autofrettage pressure |
根据DOT-CFFC标准及铝合金S-N曲线,自紧力的取值范围是49.6~59.6 MPa。
1.3.4节假设内胆残余应力可达80%屈服强度,对照图 6可知应取自紧力55.1 MPa。此时内胆在43.75 MPa载荷下的等效应力为209 MPa<SN=11 000,满足设计标准。
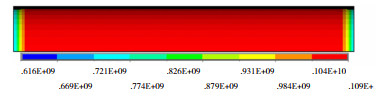
已确定铺层厚度及自紧力,为进一步验证该设计的合理性,将模拟数据与1.3节的公式计算值相比较,结果见表 3,复合材料环向应力的模拟值比计算值低4%,该偏差量在数值模拟的允许误差之内,可以认为二者吻合。自紧后循环压力上限的环向缠绕层应力如图 7所示,为1 090 MPa。
| 表 3 计算值与模拟值的比较 Table 3 Formula value compared with simulation value |
|
图 7 自紧后的环向层应力(43.75 MPa) Fig.7 Circumferential stress(43.75 MPa) |
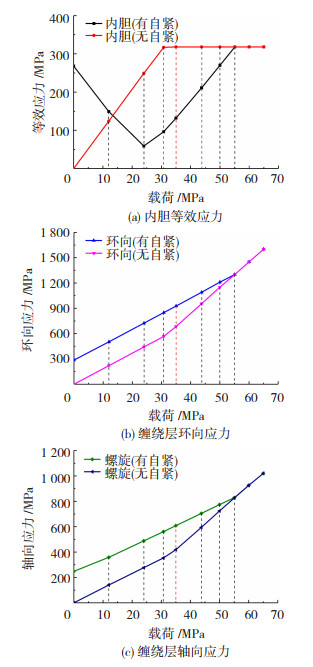
求解不同载荷条件下的应力分布,评估气瓶的综合性能,并与不施加自紧时的数据比较。各载荷下内胆等效应力、环向缠绕层环向应力、螺旋缠绕层轴向应力的应力-载荷曲线如图 8所示。
|
图 8 应力-载荷曲线对比 Fig.8 Comparison of stress-pressure load curves: (a) von mises stressofliner; (b) circumferential stress of spiral layer; (c) longitudinal stress of spiral layer |
由图 8可知,在气瓶的工作压力下,自紧后内胆等效应力降低58%,不及屈服强度的一半,疲劳性能明显改善;环向缠绕层应力增幅35%,螺旋缠绕层应力增幅45%,对碳纤维性能的利用率明显提高。
3 强度校核 3.1 气瓶爆破试验复合材料的强度极限与结构、承载形式有关。为确定环向层的强度极限,需要进行气瓶爆破试验。选择某个疲劳寿命(N>11 000),按照以上方法计算铺层厚度,制备气瓶样品,筒身环/螺交替缠绕,并对封头螺旋缠绕层采取额外补强措施。
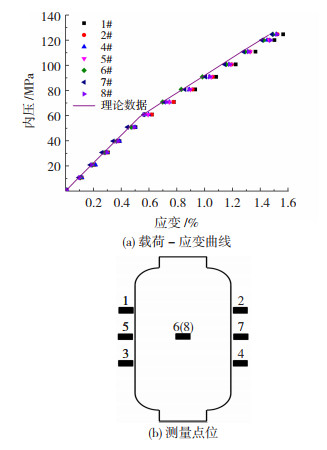
样瓶的外观及破碎内胆如图 9所示,爆破发生于筒身中部,符合预期。实测爆破压力124.6 MPa。载荷-应变曲线及测量点位如图 10所示,单轴应变片沿环向粘贴,编号1#~8#,其中3#信号中断,已剔除。实验数据稳定性良好,与理论模拟吻合。

|
图 9 样瓶外观及破碎内胆 Fig.9 Sample appearance and broken liner of burst test: (a) sample appearance; (b) broken liner |
|
图 10 爆破试验载荷-应变曲线及测量点位 Fig.10 Load-strain curve (a) and measuring position (b) of burst test |
对爆破样瓶进行有限元分析,该爆破压力下的环向层应力为2 970 MPa,如图 11所示。因此,有限元模型的环向层强度极限为2 970 MPa。

|
图 11 样瓶爆破强度模拟 Fig.11 Bursting pressure simulation of sample |
在原模型中依次计算气瓶在高压载荷下的环向应力,如图 12所示。由图可知,环向应力与载荷为线性关系,爆破强度预测值为110.6 MPa,大于最小爆破压力78.75 MPa,符合GB/T 35544标准要求。

|
图 12 设计气瓶的爆破强度预测 Fig.12 Prediction of burst strength |
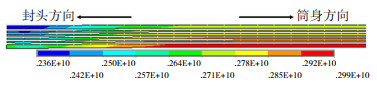
110.6 MPa载荷下气瓶环向缠绕层应力分布如图 13所示,环向危险点位于筒身,且失效原因是最内层应力2 990 MPa达到强度极限。由图 8(b)可知,公称工作压力下的环向应力为927 MPa,因此纤维应力比为2 990/927=3.2该值>2.25,满足GB/T 35544标准要求。
|
图 13 环向层危险点 Fig.13 Dangerous position of circular layer |
除环向应力外,还需计算螺旋层正轴应力及剪切应力,证明当环向层达到强度极限时,螺旋层仍处在安全状态。该数据可通过螺旋层的轴向、环向应变,经直角坐标系内的平面应变转角公式(9)、(10)得出,以逆时针为正:
| $ \begin{array}{l} {\varepsilon _\alpha }{\rm{ = }}\frac{1}{2}({\varepsilon _x} + {\varepsilon _y}) + \frac{1}{2}({\varepsilon _x} - {\varepsilon _y}){\rm{co}}{{\rm{s}}^2}\alpha + \\ \;\;\;\;\;\frac{1}{2}{\gamma _{xy}}\sin 2\alpha \end{array} $ | (9) |
| $ {\gamma _\alpha } = - ({\varepsilon _x} - {\varepsilon _y})\sin 2\alpha + {\gamma _{xy}}\cos 2\alpha $ | (10) |
式中:α为转角;εx为x向正应变;εy为y向正应变;γxy为x向剪应变;εα为α向正应变;γα为α向剪应变。
螺旋缠绕层的危险点为筒身中部和筒身-封头过渡位置,其正轴应力和剪切应力如表 4所示。
| 表 4 螺旋层正轴应力与剪切应力 Table 4 Normal stress and shear stress of spiral layer |
螺旋层正轴应力最大为2 930 MPa,低于环向最大应力2 990 MPa;剪切应力最大为23.4 MPa,远低于强度极限44.2 MPa(该剪切强度极限为试验测得)。因此,该气瓶的爆破原因是筒身环向强度不足,预期破坏位置为筒身,符合GB/T 35544标准要求。
4 结论提出一种基于铝内胆疲劳寿命设计纤维缠绕层厚度的新方法,据此设计了35 MPa工作压力铝内胆碳纤维全缠绕气瓶的铺层,构建相应的有限元模型求解合理的自紧力取值,计算了内胆及缠绕层在不同载荷压力下的应力应变分布。结合爆破试验推断了缠绕层的实际强度极限。
1) 依据网格理论、气瓶自紧原理、DOT -CFFC标准、铝合金S-N曲线,可基于铝内胆的疲劳性能设计铺层参数。有限元分析的结果显示,疲劳载荷下的缠绕层应力模拟值与设计预期吻合良好,偏差为4%。
2) 气瓶的最佳自紧力取值可根据设计预期通过有限元分析得出。施加自紧后,气瓶在常规工作压力区域内的疲劳性能、纤维性能利用率相较于未自紧时有显著提升。
3) 结合爆破试验所得数据,可以获得环向缠绕层的实际强度极限,进而预测气瓶的爆破强度、失效形式、应力比。模拟结果显示:设计气瓶的爆破强度为110.6 MPa,失效位置为筒身,失效原因为环向缠绕层的最内层达到强度极限,纤维应力比为3.22,均符合GB/T 35544标准。
| [1] |
缐永兴. 碳纤维全缠绕复合气瓶缠绕方式的设计与选择[D]. 北京: 北京工业大学, 2015. XIAN Yongxing. Winding pattern design and selection of full wrapped composite cylinders[D]. Beijing: Beijing University of Technology, 2015. |
| [2] |
林松, 牛鸿庆, 李文斌. 聚酰亚胺纤维与碳纤维缠绕复合气瓶性能对比研究[J]. 材料科学与工艺, 2018, 26(6): 23-29. LIN Song, NIU Hongqing, LI Wenbin. Comparative study on performance of polyimide fiber andcarbon fiber composite cylinders[J]. Materials Science and Technology, 2018, 26(6): 23-29. DOI:10.11951/j.issn.1005-0299.20170380 |
| [3] |
付敏, 林松, 陈亮, 等. 纤维缠绕复合材料气瓶内衬的屈曲分析[J]. 材料科学与工艺, 2015, 23(2): 86-90. FU Min, LIN Song, CHEN Liang, et al. The simulation of winding process of filament wound pressure vessel[J]. Materials Science and Technology, 2015, 23(2): 86-90. DOI:10.11951/j.issn.1005-0299.20150215 |
| [4] |
李地红, 李兴冀, 张东兴, 等. 复合材料缠绕压力容器缠绕过程模拟[J]. 材料科学与工艺, 2007, 15(5): 628-630. LI Dihong, LI Xingji, ZHANG Dongxing, et al. The simulation of winding process of filament wound pressure vessel[J]. Materials Science and Technology, 2007, 15(5): 628-630. DOI:10.3969/j.issn.1005-0299.2007.05.009 |
| [5] |
HARADA S, ARAI Y, ARAKI W, et al. A simplified method for predicting burst pressure of type Ⅲ filament-wound CFRP composite vessels considering the inhomogeneity of fiber packing[J]. Composite Structures, 2018, 190: 79-90. DOI:10.1016/j.compstruct.2018.02.011 |
| [6] |
ZU Lei, XU Hui, WANG Huabi, et al. Design and analysis of filament-wound composite pressure vessels based on non-geodesic winding[J]. Composite Structures, 2019, 207: 41-52. |
| [7] |
ZHANG Qian, XU Hui, JIA Xiaolong. Design of a 70 MPa type IV hydrogen storage vessel using accurate modeling techniques for dome thickness prediction[J]. Composite Structures, 2020, 236: 111915. DOI:10.1016/j.compstruct.2020.111915 |
| [8] |
FERNANDESL, MARTINSF R, SILVAP P. Design of a self-contained breathing apparatus (SCBA) using a carbon fibre reinforced polymer and filament winding[J]. Ciência & Tecnologia dos Materiais, 2017, 29(1): 109-113. |
| [9] |
MOHAMMAD H H, ALI T, AHMAD R G, et al. A novel detailed analytical approach for determining the optimal design of FRP pressure vessels subjected to hydrostatic loading: Analytical model with experimental validation[J]. Composites Part B, 2020, 183: 107732. DOI:10.1016/j.compositesb.2019.107732 |
| [10] |
CAMARAS, BUNSELLR A, THIONNETA, et al. Determination of lifetime probabilities of carbon fibre composite plates and pressure vessels for hydrogen storage[J]. International Journal of Hydrogen Energy, 2011, 36(10): 6031-6038. DOI:10.1016/j.ijhydene.2010.12.069 |
| [11] |
LIU Chao, SHI Yaoyao. Design optimization for filament wound cylindrical composite internal pressure vessels considering process-induced residual stresses[J]. Composite Structures, 2020, 235: 111755. DOI:10.1016/j.compstruct.2019.111755 |
| [12] |
全国气瓶标准化技术委员会. 车用压缩氢气铝内胆碳纤维全缠绕气瓶: GB/T 35544-2017[S]. 北京: 中国标准出版社, 2018. National technical committee for cylinder standardization. Fully-wrapped carbon fiber reinforced cylinders with an aluminum liner for the on-board storage of compressed hydrogen as a fuel for land vehicles: GB/T 35544-2017[S]. Beijing: Standards Press of China. 2018. |
| [13] |
许家忠, 乔明, 尤波. 纤维缠绕复合材料成型原理及工艺[M]. 北京: 科学出版社, 2013: 1-3. XU Jiazhong, QIAO Ming, YOU Bo. Forming principle and technology of filament wound composites[M]. Beijing: Science Press, 2013: 1-3. |
| [14] |
李顺林, 王兴业. 复合材料结构设计基础[M]. 武汉: 武汉理工大学出版社, 1993: 44-50. LI Shunlin, WANG Xingye. Fundamentals of composite structural design[M]. Wuhan: Wuhan University of Technology Press, 1993: 44-50. |
| [15] |
刘锡礼, 王秉权. 复合材料力学基础[M]. 北京: 中国建筑工业出版社, 1984: 199-201. LIU Xili, WANG Bingquan. Fundamentals of composite mechanics[M]. Beijing: China Architecture & Building Press, 1984: 199-201. |
| [16] |
Department of Transportation. Basic requirements for fully wrapped aluminum lined cylinders: DOT-CFFC 2007[S]. Washington: Department of Transportation, 2007.
|
| [17] |
YAHR G T. Fatigue design curves for 6061-T6 aluminum[J]. Journal of Pressure Vessel Technology, 1997, 119(2): 211-215. DOI:10.1115/1.2842286 |
 2021, Vol. 29
2021, Vol. 29


