2. 云南省冶金电极材料工程技术研究中心,昆明 650106;
3. 云南云铜锌业股份有限公司,昆明 650106
2. Yunnan Provincial Engineering Technology Research Center of Metallurgical Electrode Materials, Kunming 650106, China;
3. Yunnan Yuntong Zinc Co., Ltd., Kunming 650106, China
多年来,湿法冶金技术发展缓慢,只是作为火法冶金的一种辅助手段而逐步发展,直到19世纪才得到快速发展,并在20世纪逐渐成为冶金学科的一个独立分支。湿法冶金具有流程简单、过程组合方案多、生产成本低、规模灵活的优点,使其在现代冶金中扮演着越来越重要的作用。目前,约90%的锌和20%的铜是通过湿法冶炼提取。此外,在湿法冶炼过程中,锌电积能耗约占整个锌提取过程的80%[1],铜电积能耗约占整个铜提取过程的30%,因此电流效率和能耗问题始终是科研工作者和企业生产关注的重点。近年来,我国积极实施“三去一降一补”以及供给侧改革措施,淘汰落后产能提高生产效率,进一步突出了问题的严峻性。
如何提高电流效率和降低能耗是科学工作者和实际生产过程需要考虑的关键性问题。通过调整操作参数和提高副反应过电位来抑制阴极析氢是一个关键的途径,另一个研究的热点是开发新的电极或改善电极的质量,以延长使用寿命,从而降低操作成本。因此,为了优化运行参数,实现高效节能,人们进行了大量的实验或数值模拟预算。但是,由于系统中电解液用量大,工艺过程中的电解提取性能在参数调整和性能变化之间存在延迟,此外,旨在改善工艺性能的实验方法需要大量的时间和资金投入。因此,建模和仿真已经成为实现低成本、高效率、高柔性、高精度优化的主要途径。
在金属电积过程中,基于实验数据的电流效率预测回归方程有助于快速综合评估电流效率,且针对电积过程进行建模仿真也是一种有效手段。一般情况下,基本的电化学模型包含电化学、传质及传热等方面,有时还包括流体流动的影响。基于此,研发人员继续开发了专门用于模拟电解槽内流体流动的计算流体动力学(Computational Fluid Dynamic, CFD)模型。
本文综述了湿法炼锌和炼铜过程中的数值模拟方程和模型(分别为电流效率预测方程、相关参数经验方程、电沉积过程中的电场和流场模拟),通过对模型分析,可以预测哪一种建模方法将有助于金属电积工艺的发展。
1 模拟仿真在湿法炼锌中的应用 1.1 电流效率预测方程在湿法炼锌中的应用电流效率预测方程最初是由Wark[2]提出,电流效率与硫酸锌浓度之比的半经验关系式可通过以下公式得出:
| $ \frac{\beta }{{1 - \beta }} = \frac{1}{k}\frac{{{C_{{\rm{ZnS}}{{\rm{O}}_4}}}}}{{{C_{{{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}}}}} $ | (1) |
式中:β为电流效率,%;k为常数;CZnSO4为ZnSO4浓度,mol/L;CH2SO4为H2SO4浓度,mol/L。
此方程是基于高纯度溶液实验结果得到。用不同的ZnSO4/H2SO4值(比率0.09~5)进行测试,并将测量结果与方程(1)(k值为30)的预测结果进行比较,发现结果达到了非常好的吻合,且作者指出方程(1)中的k值几乎与温度、电流密度和沉积周期无关。Bratt[3]将以上得到的电流效率与ZnSO4/H2SO4值的关系称其为“沃克规则”,并指出镍电沉积中也存在上述类似的关系,这也为这一规则提供了进一步支持。正如Wark[4]在其他工作中所讨论的那样,此规则仅适用于高纯度电解液,因此仅适用于特定条件,在实际电积中的应用有限。
Ivanov[5]研究了锑、锗、镍离子以及有机添加剂对硫酸锌电解液锌电积过程的影响。结果表明,金属杂质会降低锌电积过程的电流效率;有机添加剂的添加则会提高电流效率,改善镀层质量。Recendiz等人[6]研究了3种添加剂对锌电积过程的影响,发现所有存在添加剂时的电流效率均大于不含添加剂时的电流效率。Mackinnon等人[7]研究了15种杂质的个体效应及其与胶水的相互作用对锌电积过程的影响,并得出了在周期表的每个周期中,电流效率随着杂质元素原子数的增加而周期性地下降的结论。
电流效率预测方程在给定的参数条件下可以对电流效率做出比较可靠的预测,但是给定的条件过于理想化,在实际的电积中应用有限,未来应多结合生产实际对电流效率做出可靠的预测。
1.2 相关参数方程在湿法炼锌中的应用在实验研究的基础上,已有科学工作者[8-9]进行了各种研究以获得基于实验结果的相关物理或化学常数的经验公式。电解液的电导率、密度、粘度和溶液中各种离子的扩散系数是决定锌电积过程是否可控的关键参数。关于基本常数的经验公式也是发展基本模型所必需的,获得的常数的准确性决定了相关方程的可靠性。例如,Gueera[8]获得的电解质密度和粘度的经验方程如式(2)~(4)所示:
| $ \begin{array}{l} \rho {\rm{ = }}1011.261.1{C_{{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}}(1 - 0.08M) + 156.8M - \\ (0.44 + 0.08{C_{{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}} + 0.13M)(T - 273) \end{array} $ | (2) |
| $ \begin{array}{l} M = {C_{{\rm{Z}}{{\rm{n}}^{{\rm{2 + }}}}}} + 0.83{C_{{\rm{M}}{{\rm{n}}^{{\rm{2 + }}}}}} + 0.68{C_{{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}}} + 0.32{C_{{\rm{N}}{{\rm{a}}^{\rm{ + }}}}} + \\ 0.37{C_{{{\rm{K}}^{\rm{ + }}}}} \end{array} $ | (3) |
| $ \begin{array}{l} \eta = (17.7 + 4.1{C_{{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}} - (1.0 + 2.5{C_{{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}}({C_{{\rm{Z}}{{\rm{n}}^{{\rm{2 + }}}}}} + {C_{{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}}}))) \times \\ \exp (\frac{{15200 + (1580 + 225{C_{{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}}})({C_{{\rm{Z}}{{\rm{n}}^{{\rm{2 + }}}}}} + {C_{{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}}})}}{{RT}}) \times \\ {10^{ - 7}} \end{array} $ | (4) |
式中:CM为金属离子浓度,mol/L;CH2SO4为硫酸浓度,mol/L;T为电解液温度,K;ρ为电解液密度,kg/m3;η为电解液粘度,Pa ·s。
同样,溶液中存在的主要离子的扩散系数对传质过程也有重要影响,离子的扩散系数随操作参数的变化而变化,这也为研究提供了另一种不确定性。通常,沉积物以外的其他物质的扩散系数可以用Stokes-Einstein方程来确定。为了准确起见,沉积物种的扩散系数是根据相关实验结果导出,并且扩散系数可能与某些操作参数成函数关系,例如,对于锌电积系统,模型应考虑4个关键离子,即Zn2+、H+、HSO4+和SO42+。其中H+、HSO4+和SO42+的扩散系数由Stokes-Einstein方程确定,同时,已经有很多研究对Zn2+的扩散系数进行了讨论[8, 10-11], 其中Zouari和Lapicque’s[10]总结的经验公式如下:
| $ {D_{{\rm{Z}}{{\rm{n}}^{{\rm{2 + }}}}}} = 0.78 \times {10^{ - 6}}\exp (\frac{{ - 2186}}{T}) $ | (5) |
式中:T为电解液温度,K;DZn2+为锌离子扩散系数,m/s2。
与扩散系数计算类似,对锌的传质系数[12-13]的研究已有展开,提出了一些比较实用的经验公式,但是正如Guerra等人[8]所讨论,对以上这些方程进行选择时会存在一定的挑战性,因为每一个方程都有特定条件或成分,且可靠的预测只能在很窄的参数范围内给出。
1.3 流场模拟在湿法炼锌应用随着计算机科学的不断发展,利用计算机进行模拟仿真正越来越多的被人们所接受,且利用计算机模拟可以通过三维可视化的图形来直观形象的呈现仿真结果。
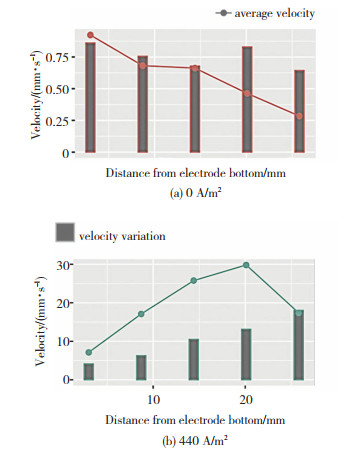
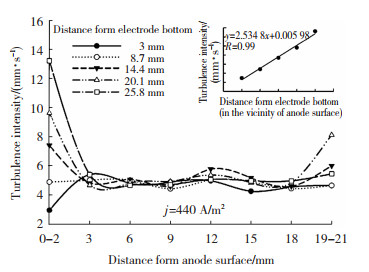
基本电化学模型只能提供关于锌电解槽一般信息,与之相比,一个包含流体流动的三维模型可以更准确的描述锌电积过程中电解液的流场分布情况。锌电解槽是一种典型的垂直平面电极反应(VPERGE)[14]体系。进入、通过和离开电解槽的电解液的流体动力学是众多因素中最有影响的工艺参数,因此,电极间隙间电解液的流体动力学特性对锌电积有重要影响。Zhou等人[15]在对锌电解沉积中气液两相流的数值模拟中发现,向上的电解液流速由于气泡运动引起的阻力而增加,使得电极之间的平均流速比没有气泡时大1.5~2.4倍。JinLuo等人[16]采用粒子图像测速技术(PIV)对锌电解槽垂直面电极附近的流场进行了可视化研究,应用电流密度为0 A/m2的比较实验(FN)和电流密度为440 A/m2的恒电流电解实验(FW),研究和比较了泵诱导和气泡诱导流动对电积表面流场的影响。研究发现,在存在上升的电解液气泡的情况下,在选定区域FW的平均流速(13.16 mm/s)几乎是FN平均流速(1.49 mm/s) 的9倍,即气泡在间隙中诱导的电解液对流程度比入口电解液的对流更强。因此可以推断,气泡流不是造成锌电解槽入口和出口之间产生压差的原因,而应该是新电解液流入电极板间隙的主要驱动力。对于电解液而言,虽然锌的质量浓度高达45~50 g/L,但其在入口和出口之间的浓度差仅为2 g/L。因此,气泡流引起的对流已经足够强,足以使电解质均匀化,从而减小扩散层的厚度。考虑到这一点,研究者最终认为通过改变流场(如增加进料速度和改变进料角度)来改善电解槽的传质特性,对锌电积过程中的电化学反应影响有限。以上结论也得到了Schilling等人[18]模拟结果的支持,假设两相流诱导的混合在电极表面附近足够强的情况下,离子浓度梯度可以忽略不计。FW比FN在电极表面不同高度处的瞬时液速变化要大得多,如图 1所示。图 2显示了从阳极表面到阴极表面不同高度的湍流强度,Y方向的速度波动是合成速度波动的主要原因,电极表面附近的湍流强度远大于间隙主体区域的湍流强度。这与Boissonneau和Byrne[19]的研究结果一致,即由于没有气泡,通道中心的流动是层流,而流体中的湍流和层流特性可以在同一水平面上跨电解通道共存。
|
图 1 不同高度阳极表面附近(2 mm以内)的平均速度和时间变化[16] Fig.1 Average speed and time change near the anode surface of different heights (within 2 mm): (a)0 A/m2; (b)440 A/m2[16] |
|
图 2 从阳极表面到阴极表面不同高度的湍流强度[16] Fig.2 Turbulence intensity at different heights from anode surface to cathode surface[16] |
在锌电积过程中,电解槽内的电解液流动方式对电流效率有重要影响。从锌电积动力学分析可知,电解液流动是锌电解槽内离子运动的主要驱动力,并能带走锌电解槽内的反应热。因此,提高电解液流量对降低电积过程电耗具有重要意义[19]。
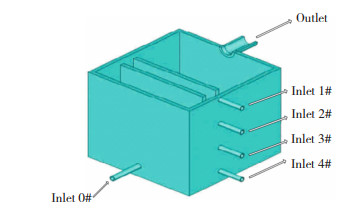
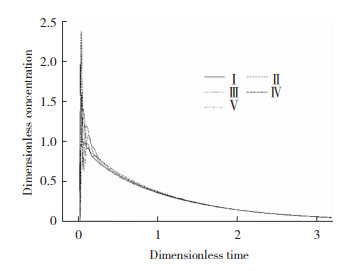
Wang等人[20]建立了锌电解槽内电解液的三维数学模型,并利用ANSYS FLUENT软件求解,研究了锌电解槽内电解液的流场和停留时间分布(RTD)。Wang等人[20]使用的锌电解槽如图 3所示,电解槽有5个入口和1个出口,0号入口和出口位于电解槽的两个相对面上,这是传统的进液方案,其他入口(1~4号)与0号入口垂直。探讨了5种不同进液方式对锌电解槽内电解液流动及停留时间分布的影响,具体进液方案如表 1所示,值得注意的是,为了简化数学模型,在计算电解液流动时,研究者忽略了电解液温度和密度、锌电解沉积、外加电场以及其气泡运动等因素,将流场视为稳态。结果表明,由于阴极与阳极之间的电解质流场较好,进液方式Ⅲ呈现最长的平均停留时间,同时死区体积分数最小(图 4)。此后,进一步对5种进液方式下锌电积过程中电流效率进行了数值模拟,得出结果如表 1所示,与传统进液方式Ⅰ相比,3种新型进液方式的电流效率有了很大的提高,尤其是对于进液方式Ⅲ,电流效率提高到98.90%,这说明通过改变进液方式,加强阴极与阳极间的电解质流动,有助于锌离子向阴极的传递和反应热的释放,对提高电流效率非常有效。
| 表 1 锌电解槽的5种进液方式和电流效率[20] Table 1 Five feeding methods for zinc electrolytic cell and corresponding current efficiency[20] |
在锌电积过程中,电积产生的气泡以及电解液的进液方式会对电解槽中电解液的流动产生显著影响。因此,未来在优化锌电解过程中电解槽的流体力学时,电积产生的气泡的流动行为以及电解液的进液方式应该被优先考虑。
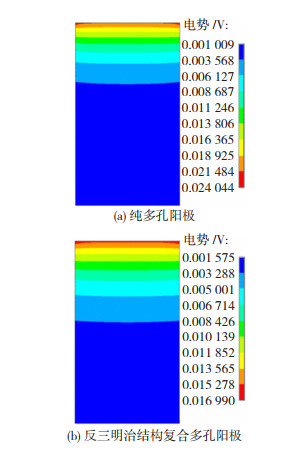
1.4 电场模拟在湿法炼锌中的应用锌电积过程的模拟计算是电场、流场以及磁场等多物理场的耦合,其中准确地获得电场分布是计算其他物理场分布的重要前提。黎红兵等人[21]基于ANSYS有限元分析软件,构建了Pb合金阳极的电化学数值计算模型,对比分析了普通多孔阳极和反三明治结构多孔Pb合金阳极在电化学反应过程中的电化学性能。两种阳极的表面电势仿真结果如图 5所示,结果表明,反三明治结构复合多孔阳极表面电势较纯多孔阳极明显均匀,前者极值差为15 mv,后者为23 mv,这说明复合多孔阳极可以降低电积过程的槽电压,减少能耗。
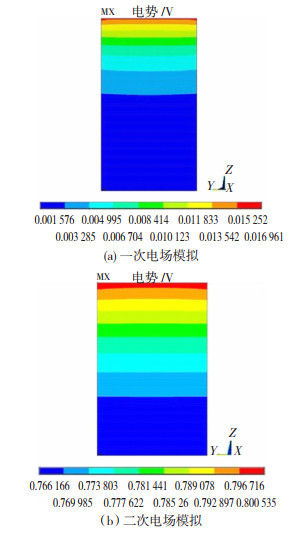
在两种阳极数值模拟研究的基础上,黎红兵等人[22]进一步做了锌电积用阳极的电场分布仿真计算。基于ANSYS12.0软件,将一次电场分布模型改进为考虑电化学反应的二次电场分布模型,并将两种模型做了对比分析,结果如图 6所示。
|
图 6 阳极电势分布[22] Fig.6 Anode potential distributions: (a) primary electric field simulation; (b) secondary electric field simul ation[22] |
结果表明,二次电场模型计算得到的阳极电阻电压降为0.034 V,这与文献报道的实际值十分接近[23],而一次电场模型的计算值仅为0.015 V,明显偏小,这说明二次电场模型得到的阳极电阻电压降更为明显。
1.5 锌电积模拟关键工艺参数在湿法炼锌中的应用电积实验是研究电解工艺参数的可靠方法,但随着操作变量(如酸浓度、锌浓度、温度、电流密度)的增加,所需的实验数量就会大大增加。此外,锌电积是一个动态过程,溶液中的成分随着电积的进行不断变化,基于这一情况,虽然已经建立了很多锌电积的模型,但这些模型大多都是理想化模型,忽略了参数变化对锌电积的影响,因此锌电积过程关键工艺参数模拟被一些科学工作者所关注。过程模拟是一种可以对锌电积过程实时监控的动态模拟,其有助于帮助工程师快速、安全地测试新的过程设置,并预测结果。
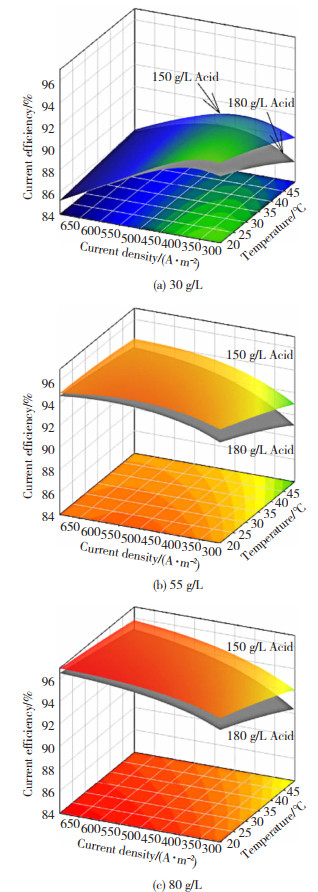
对于锌电积的最佳工艺条件已经有大量科学工作者进行了研究[24-26]。Michael等人[27]提出了一种新模型,该模型采用单个锌电解槽进行模拟,分析了锌浓度、酸浓度、温度和电流密度等变量间复杂的相互作用对电积锌过程的影响。通过对单电解池优化,发现电流密度对锌产量和能耗的影响最大,在高电流效率下,电流密度几乎与产量和能耗成正比,然而,电流密度对最佳电流效率没有类似的影响,因此电流密度与电流效率的影响并不统一。图 7显示了不同Zn2+浓度、不同电流密度、不同温度对锌电积电流效率的影响,在图 7(a)和(b)中,当电流密度较低时,较低的温度下电流效率较高,而当电流密度增高时结果相反。然而图 7(c)则显示在整个曲线图中,较低的温度会使电流效率处在一个较高的水平。这是因为较低的温度导致交换电流密度、标准速率常数、平衡电势以及阴极处氢气体积流量降低,从而导致传质系数的降低。从图 7(a)~(c)中还可以注意到,随着锌浓度的增加,最大电流效率向更高的电流密度移动,这表明限制电流密度对电流效率有很大影响。
|
图 7 不同Zn2+浓度下单个电解槽电流效率的表面响应曲面图[27] Fig.7 Response surface plot of current efficiency of a single electrolytic cell under different Zn2+ concentrations: (a)30 g/L; (b)55 g/L; (c) 80 g/L[27] |
从优化结果中可以看出,低极限电流密度和由此产生的低电流效率对能耗的影响可以在图 8(a)中看到。与图 8(a)的结果相反,图 8(b)、(c)的相似性表明,在极限电流密度较大的区域,增加的锌浓度对能量消耗没有大的影响。由于产生驱动阳极和阴极反应所需的过电压以及使大量电流通过电解质所需的电池电压增加,预计能量消耗会随着电流密度的增加而普遍增加。因此,能耗表面图的变化必须是电池电压竞争性变化的结果。

|
图 8 不同Zn2+浓度下单个电解槽的能量消耗的表面响应曲面图[27] Fig.8 Response surface plot of energy consumption of a single electrolytic cell under different Zn2+ concentrations: (a) 30 g/L; (b) 55 g/L; (c) 80 g/L[27] |
Mn2+同样是锌电积过程研究的一个热点。锌电积电解液中需要少量溶解的锰,以便形成一个薄层二氧化锰来减少阳极腐蚀。通常,Mn2+的浓度一般为3~4 g/L,以促进阳极氧化保护。然而,由于电解池内存在影响Mn2+消耗的竞争因素,控制恒定的Mn2+浓度来维持MnO2涂层是相对困难的。
同时,因为很难在实验室中复制常规速率测试的条件,所以电解过程锰的消耗率很难计算。并且,直接从电解过程统计数据来计算锰的消耗速率也会带来误差,这是因为随着Mn2+浓度的变化,新的进料电解液的电解质也会随之发生变化,然后通过电解液再循环,这使得确定一个一致的计算基础变得困难。因此,模拟提供了一种复制生产实际溶液流动和浓度的方法,以获得对大数据的预测,也可用于密切追踪锰的浓度,以观察过程变化或者生产过程中某些不稳定因素是否对猛消耗率有明显影响。
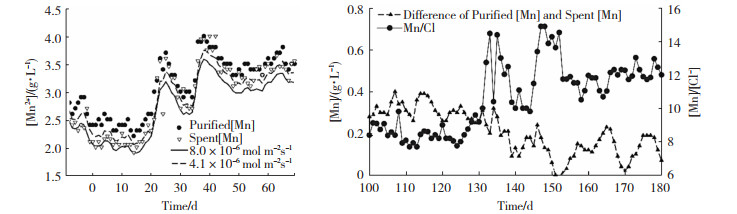
Mahon等人[28]使用与工业电解槽数据相结合的过程模拟来研究锌电解过程中锰的消耗。为了用反应速率的静态值来表示锰的氧化,在模拟中引入了锰的消耗率。假设总速率代表已建立的阳极,该速率在两个不同的时间段内进行,其中锰的消耗浓度分别处于约2.0和3.8 g/L的设定值。研究者通过一个单纯型优化算法来确定速率,该算法通过改变消耗速率,寻求用最小二乘和函数最小化预测和测量锰浓度之间的差异。通过过程模拟发现,在平均Mn2+浓度为3.8 g/L时锰的消耗速率为4.1×10-6 mol/(m2 ·s),而在Mn2+浓度为2.0 g/L时,锰的消耗速率为8.0× 10-6 mol/(m2 ·s)。从图 9(a)中可以看出,Mn2+浓度增加前后的静态速率分别为4.1×10-6 mol/(m2 ·s) 和8.0×10-6 mol/(m2 ·s)。利用过程模拟确定的速率表明,锌电积电池室中锰的消耗速率在不同电积过程是不同的,造成这种差异的原因还有待进一步研究,但不可否认动态模拟是计算工厂锰的总消耗率的有用工具。
|
图 9 不同条件下Mn2+消耗率和浓度比: (a)两种不同恒定锰消耗率随锰浓度增加的预测值和测量值的比较;(b)净化和废电解液锰浓度(左轴)与废电解液中锰与氯化物浓度之比(右轴)之间的差异。[28] Fig.9 Mn2+ consumption rate and concentration ratio under different conditions: (a) comparison of predicted and measured values of two different constant manganese consumption rates with increasing manganese concentrations; (b) difference between purified and spent electrolyte manganese concentrations (left axis) compared with the ratio of manganese to chloride concentrations in spent electrolyte (right axis)[28] |
杂质可能对锰离子的消耗有影响。目前,有研究确定Cl-与锌电解质中的Mn2+存在相互作用[29],通过对电解废液中Cl-的浓度研究发现,Mn消耗量较大的时期似乎与氯化物水平的高低无明显关系。同时,在这段时间内,Cl-浓度也没有很大的变化。然而,操作员通常会控制Mn与Cl-的比率,而不是单独控制某一浓度,并向净化电解液中添加更多的锰,以便在电积过程中保持6 ∶1或更高的比率(取决于操作偏好)。锰与氯浓度的低比率似乎与锰的消耗增加一致,反之亦然。在图 9(b)中,当该比率约为9或更少时,锰的消耗量更大,如纯化锰和废电解液锰浓度差的增加所示。这表明锰与氯的比率对锌电解槽中锰的消耗有一定的影响。
对锌电积过程中关键工艺参数进行模拟有助于把握电积过程中关键离子的相互作用规律,对指导企业生产有重要意义。基于当前锌矿石中的杂质含量越来越高这一现状,通过研究电积过程中杂质离子的作用规律,优化企业生产显得至关重要。
2 模拟仿真在湿法炼铜中的应用目前火法精炼工艺产出的精铜一般含铜99.2% ~ 99.7%,还有大约0.3% ~ 0.8%的杂质。杂质中通常包括一些显著降低铜质量的O、S、Sb、Bi、As、Pb等,还包括一些价值较高的金属Au、Ag、Ni等,可回收利用,因此火法精炼产出的铜还需要进行电解精炼。目前铜电解精炼[30]生产向大型化、大极板化、自动化、高效率、高质量、低消耗、低成本等目标发展。在当今生产形势下,为了提高产能、降低能耗,大量生产技术人员和科研人员结合当前铜电解生产实际,采取了严格控制相关电解工艺技术条件、节能工艺等一系列有力措施[31-34],这些措施已经通过实践证明确有良好效果,但这些措施多为生产经验和实验研究,缺乏理论依据的支撑,因此很有必要对铜电解过程进行建模仿真研究,为实际生产提供理论依据。
众所周知,铜电解过程涉及电解液的循环流动、传热、扩散传质和导电等多种物理传递和复杂的化学、电化学反应,其中交互影响电解液传递的物理场[35-39]有流场、温度场、电场和浓度场等,本文将对流场和电场对铜电解过程中的影响做详细阐述。
2.1 流场模拟在湿法炼铜中的应用工业上铜电解通常是在大型矩形电解池中进行,在这种电解池中,大量的交替阴极和阳极板垂直堆叠,通过电极之间的电流使铜离子沉积在阴极上,同时在阳极上产生氧气泡。上升的氧气泡会在电极之间的空间中形成一个大的再循环区,这种再循环对向阴极的传质有很大的影响[40]。气泡产生再循环的计算流体动力学(CFD)模型可以深入了解板间空间中电解液的流体动力学行为,并开以了解铜向阴极不同部分传质的细节。CFD技术主要是利用计算机将实际的流体问题转为数学模型,然后通过对数学模型中的动量、能量、质量守恒方程进行求解,来模拟实际生产过程中难以检测和控制的反应过程。张强等人[41]综述了CFD技术在湿法冶金中的应用,并对CFD技术在搅拌釜模拟中的应用做了重点阐述,最后他指出CFD技术在湿法冶金中的应用主要有以下3个方面:一是加强对高固体模拟方向的研究;二是进一步研究除液-固、气-液项以外是否存在第三项;三是有必要探索化学反应模型与CFD模型相结合这一潜在方向。Leahy等人[42]建立了一个计算流体动力学模型,用来模拟由单阳极-阴极对组成的电解槽中气泡驱动的流体力学和Cu2+的分布。当模拟运行到一个准稳态时,其整体变量值的变化很小,结果如图 10所示(所有图沿Y方向按因子3拉伸)。

|
图 10 CFD模拟结果[43]: (a)电解质速度向量场; (b)铜浓度等值线; (c)氧体积分数(-)等值线; (d)涡流粘度比等值线; (e)速度等值线; (f)电解质流线[42] Fig.10 CFD simulation results[43]: (a) electrolyte velocity vector field; (b) copper concentration contour; (c) oxygen volume fraction (-) contour; (d) eddy current viscosity ratio contour; (e) velocity contour; (f) electrolyte streamlines[42] |
图 10所示的结果是二维横截面,阳极在右侧(高Y),阴极在左侧(低Y),电解液从右侧的阳极进入。图 10(a)~(f)分别显示了速度矢量场、铜浓度等值线、氧体积分数、湍流涡流粘度比、速度和流线。铜浓度等值线如图 10(b)所示,可以看出整个电极间隙浓度是均匀的,并且在离阴极很近的区域浓度较低。图 10(c)所示的氧体积分数等值线可以看出,由于气泡体积尺寸较小,气泡在再循环中被再次夹带。在电极间隙顶部,氧体积分数约为2.5%,在中间高度处,随着电解池深度的增加,氧体积分数逐渐减小至可忽略不计。之所以设置这种分布,是因为气泡被向下拖至向下流速刚好足以克服(向上)浮力的点;即向下的电解质速度等于向上的气泡滑移(终端)速度,此时气泡的尺寸为150 μm,可以看出不同尺寸的气泡会将气体夹带到稍微不同的深度。图 10(d)显示,湍流涡流粘度比(湍流与层流粘度之比)是湍流强度的量度,在阳极板附近(其中上升的气泡导致电解质中显著的速度剪切)和朝向板对顶部(强再循环区出现在该处)最高。在图 10(e)所示的速度图中可以看到这些较高的速度区。涡流粘滞比在间隙下部最低,靠近阴极。并且他指出,后续应辅以实验来验证沿阴极和阳极形成的CFD预测的涡流,尤其是沿阳极形成的涡流以及与它们相关的氧气气泡向主体内的喷射和相互影响。
铜电解过程中的计算流体动力学(CFD)模拟一直是众多论文的研究主题,且流体动力学中的自然对流通常在小规模试验区[43-46]或者在大型二维域[47]中进行模拟。Kemminger和Ludwig[48]对全尺寸铜电解精炼槽内电解液的流动进行了计算流体动力学模拟。模拟分成两个部分进行,即首先进行局部模拟再进行全局模拟。局部模拟研究了电极上发生的自然对流,研究区域包括一个阳极和两个阴极。
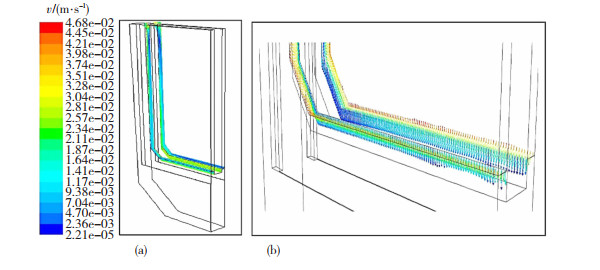
通过假设域正面和背面不同的入口和出口条件进行了几次局部模拟。结果表明,电极之间的流动受入口和出口条件的影响很小,连接局部和全局模拟的界面处的流场,如图 11所示,似乎是一个流场研究中的一个非常常见的流场,主要取决于阳极和阴极之间发生的反应,受全局流的影响很小。连接局部模拟和全局模拟共有120个接口,这些接口处的入口速度分布全部采用图 11所示的速度分布。
|
图 11 连接局部和全局模拟的界面处的速度分布(a)和底部界面的详细视图(b)[48] Fig.11 Velocity distribution at the interface connecting local and global simulations (a) and detailed diagramof bottom interface (b) [48] |
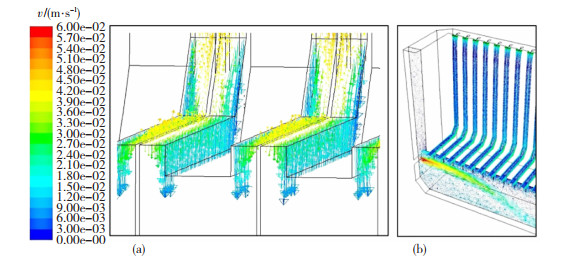
在局部模拟的基础上,Kemminger和Ludwig[48]进一步进行了全局模拟,通过全局模拟计算了120个接口处的自然对流和强制对流共同作用下的槽内流场。图 12显示了模拟获得的接口的输入值,新鲜电解液泵入和泵出电解槽所产生的强制对流在入口处形成自由入射流,这个自由入射流与阴阳极之间的自然对流相互作用而被向下推动。这种模拟方法克服了当前计算机硬件方面的不足,对大型的流场域模拟具有积极的指导意义。
|
图 12 将局部模拟获得的速度剖面作为120个接口处的全局模拟的边界条件(a)及从入口处流出的新鲜电解液与阳极间隙产生的自然对流相互作用(b)[48] Fig.12 Velocity profile obtained fromlocal simulation andused as boundary conditions for global simulation at 120 interfaces (a) and natural convection interaction produced by fresh electrolyte flowing from inlet and anode gap (b) [48] |
对铜电积流场进行模拟研究将有助于帮助我们了解电解液在电解槽中的流动形式,在未来的工作中,应辅以相应的实验对模拟研究的结果加以验证,此外,流场对阴极铜产量的作用关系有待进一步研究。
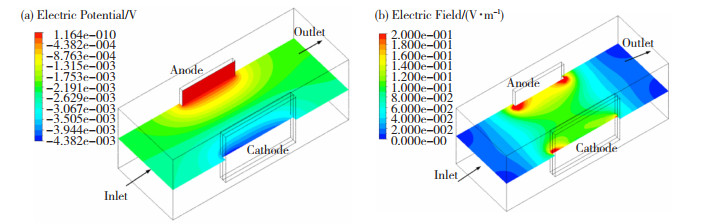
2.2 电场模拟在湿法炼铜中的应用近年来,计算机模拟在电化学系统的设计和性能评估中的重要性显著提高。电解模型为工程师提供了研究电解池几何形状和操作条件对冶金过程影响的可能[49-52]。加速计算机模拟技术发展的最有效的方法是建立潜在的电化学和传输过程的物理模型。Kim等人[53]将电化学动力学与离子在电解液中的流动通过简化的铜电解槽的三维运输模型进行完全耦合模拟。采用电化学反应模型的耦合方法,研究了离子输运与固体电解质流动的依赖性。对于电极反应与电场模型,通常使用极化方程来表示电化学反应的局部速率与不同浓度的电解液在电极处的电位降的关系,这种关系通常使用金属/离子体系形式的电极动力学的Tafel近似[54]的方法来表征。如果阴极侧的沉积速率集中在模拟方法上,则可以假定在恒定的外加电流条件下阳极反应的速率是可逆的。这种假设是基于阳极无表面过电位的理想情况。图 13(a)显示了通过阳极和阴极之间的电解质区域与阴极的过电位耦合的电势分布模式(横截面图)。由于此处假设阳极接地为0 V,因此可以使用混合边界条件,根据给定的通量(来自Tafel动力学的电流密度)计算阴极处的电位。由于电解液的导电性,使接地阳极的电位增加,这就是欧姆电位降,它反映了电解液区电子传输阻力相关的损耗。电极间电场的模拟如图 13(b)所示,空间电流密度局部与电位梯度成正比。这些都是通过浓度梯度和表面过电位的耦合计算得出的结果。
|
图 13 电流100 A/m2,入口速度0.2 m/s时阳极和阴极之间的电势分布(a)和电场(b)[53] Fig.13 Electric potential distribution (a) and electric field (b) between anode and cathode when current is 100 A/m2 and inlet velocity 0.2 m/s[53] |
为了增进局部电流密度的准确预测,Werner等人[55]证明了一个基于COMSOL的多物理模型来预测铜电解槽阴极局部电流密度分布的有效性。作者提出了将Nernst-Planck输运方程与电极动力学耦合起来,以及结合Euler-Euler两相CFD法的方法框架,并通过实验来验证模拟结果。图 14(a)显示了用于验证3种不同电极的,作为电解池中典型的几何现象的代表,模拟结果如图 14(b)~(d)所示。图 14(b)为直阴极板模型模拟结果,它将60~90 s时阴极的平均模拟电流密度与根据沉积厚度确定的电流密度进行比较,可以发现,测量的电流密度和模型数据基本一致,两者电流密度之间最大的表观差异是表观粗糙度。图 14(b)中所示的电流密度变化由两个因素引起:一是实际沉积物粗糙度不同;二是用于测量表面的三维扫描仪的分辨率不足,并将测量值离散成表面网格进行测量的缘故。对于倾斜阴极,图 14(c)显示了从实验到模型的电流密度对比,这将有助于与图 14(b)中的直板几何形状进行对比。

|
图 14 铜电解阴极局部建模与仿真结果:(a)用于验证的电极几何形状;(b) 结瘤阴极的平均电流密度分布的实验与模拟对比;(c)直阴极;(d)倾斜阴极;(e)结瘤表面图形[55] Fig.14 Partial modeling and simulation results of copper electrolysis cathode: (a) electrode geometry used for verification; (b) comparison between experiment and simulation results of average current density distribution of nodulecathode; (c) straight cathode; (d) inclined cathode; (e) nodular surface pattern[55] |
相比之下,由于局部电流密度较低,倾斜的阴极在阴极顶部形成不太明显的脊。倾斜阴极上的最大电流密度位于距阴极底部约0.02 m,最靠近阳极的位置。这是因为电解液与阳极之间的距离减小,电位降较低,电极动力学使电流密度有所降低。电流密度增加的最大值为0.025,这是由于阴极靠近阳极底部所导致的,距离减小导致的电解液电阻降低是电流密度增加的原因。根据欧姆定律,较低的电阻会增加流向该区域的电流。图 14(d)显示了结瘤阴极电流密度实验与模拟结果的比较。除结瘤组织外,模型与实验结果达到了较好的吻合。模型在结瘤组织处与实验结果吻合度较低,这可能是由于模型是根据沉积厚度确定电流效率的方式造成的。此外,可能是由于图 14(e)所示的额外结瘤存在的原因,导致最大电流密度低于130 A/m2。由于采用数值积分法确定结瘤沉积厚度,所以采用相邻数据点之间的中心平均值,这就是为什么在图 14(d)中,结瘤底部的电流没有达到零。
电场模拟有助于帮助我们观察电积过程中电解槽及极板上的场强分布,但是单一的电场模拟忽略了溶液的传质传热以及电解液的流动,是一个理想化模型,未来的研究应将电场和流场耦合模拟,使模拟数据更加真实可靠。
3 结论与展望电积过程的电能消耗是湿法冶炼过程中能源消耗的主要部分,因此在电积过程中提高电流效率和降低能耗是关键。在电化学过程中通过模拟电极动力学的电化学模型优化工艺条件是必不可少的。主要的电化学模型包含电场、传质、传热等过程,有时还有流体流动的影响。本文讨论总结了一些相关的、已通过实验或工业数据验证的模型,但在建模过程中忽略或简化了实际电积过程中的一些重要特征。为了实现更为结合工业现场的模拟,未来的模型应该关注三维两相流、电化学、传质和传热等之间的耦合,以及电积过程中由于沉积所产生的极板的几何变形等因素。然而,这种考虑整个单元的综合模型将需要高度耦合的物理和化学,并且比简化模型或经验模型需要更多的计算能力,这也是在上述模型中进行假设和简化的最重要原因之一。但通过整合锌电积和铜电解工艺和所有关键因素来提高模型的准确性,将会有助于开发更为有效和经济的生产工艺。
| [1] |
XU X, LI D, CHEN L, et al. Improve the energy efficiency: Effects of additives on longtime zinc electrowinning[J]. Hydrometallurgy, 2020, 193: 105326. DOI:10.1016/j.hydromet.2020.105326 |
| [2] |
WARK I W. Electrochemistry: proceedings of the first australian conference on held in sydney, 13-15th february and hobart, 18-20th february 1963[M]. Elsevier, 2013.
|
| [3] |
BRATT C G, AURELL M, NILSON S. Renal function in patients with hydronephrosis[J]. BritishJournal of Urology, 1977, 49(4): 249-255. DOI:10.1111/j.1464-410X.1977.tb04130.x |
| [4] |
WARK I W. The electrodeposition of zinc from acidified zinc sulphate solution[J]. Journal of Applied Electrochemistry, 1979, 9(6): 721-730. DOI:10.1007/BF00614966 |
| [5] |
IVANOV I. Increased current efficiency of zinc electrowinning in the presence of metal impurities by addition of organic inhibitors[J]. Hydrometallurgy, 2004, 72(1-2): 73-78. DOI:10.1016/S0304-386X(03)00129-4 |
| [6] |
RECÉNDIZ A, GONZÁLEZ I, NAVA J L. Current efficiency studies of the zinc electrowinning process on aluminum rotating cylinder electrode (RCE) in sulfuric acid medium: Influence of different additives[J]. Electrochimica Acta, 2007, 52(24): 6880-6887. DOI:10.1016/j.electacta.2007.04.112 |
| [7] |
MACKINNON D J, BRANNEN J M, FENN P L. Characterization of impurity effects in zinc electrowinning from industrial acid sulphate electrolyte[J]. Journal of Applied Electrochemistry, 1987, 17(6): 1129-1143. DOI:10.1007/BF01023596 |
| [8] |
GUERRA E, BESTETTI M. Physicochemical properties of ZnSO4-H2SO4-H2O electrolytes of relevance to zinc electrowinning[J]. Journal of Chemical & Engineering Data, 2006, 51(5): 1491-1497. DOI:10.1021/je0600911 |
| [9] |
MAHON M, WASIK L, ALFANTAZI A. Development and implementation of a zinc electrowinning process simulation[J]. Journal of the Electrochemical Society, 2012, 159(8): D486. DOI:10.1149/2.084208jes |
| [10] |
ZOUARI I, LAPICQUE F. An electrochemical study of zinc deposition in a sulfate medium[J]. Electrochimica Acta, 1992, 37(3): 439-446. DOI:10.1016/0013-4686(92)87033-V |
| [11] |
CATHRO K J. Mass transport during zinc electrowinning at high current density[J]. Journal of the Electrochemical Society, 1992, 139(8): 2186. DOI:10.1149/1.2221200 |
| [12] |
BISWAS S, SEN T K, Yeneneh A M, et al. Synthesis and characterization of a novel Ca-alginate-biochar composite as efficient zinc (Zn2+) adsorbent: Thermodynamics, process design, mass transfer and isotherm modeling[J]. Separation Science and Technology, 2019, 54(7): 1106-1124. DOI:10.1080/01496395.2018.1527353 |
| [13] |
ANARI Z, KATOOZI E, Sengupta A. Establishing correlation between effective diffusivity coefficient and the mass transfer for Zn2+ column extraction by D2EHPA: An experimental and theoretical investigation[J]. Journal of Environmental Chemical Engineering, 2018, 6(5): 6322-6327. DOI:10.1016/j.jece.2018.09.059 |
| [14] |
HREIZ R, ABDELOUAHED L, FUENFSCHILLING D, et al. Electrogenerated bubbles induced convection in narrow vertical cells: PIV measurements and Euler-Lagrange CFD simulation[J]. Chemical Engineering Science, 2015, 134: 138-152. DOI:10.1016/j.ces.2015.04.041 |
| [15] |
ZHOU P, LI H, WEI W, et al. Numerical simulation of gas-liquid two-phase flow in zinc electrowinning[J]. Journal of Northeastern University (Natural Science), 2015, 36(8): 1136-1140. DOI:10.12068/j.issn.1005-3026.2015.08.016 |
| [16] |
LUO J, JIAO P P, DUAN N, et al. Flow field characterization in the vicinity of vertical plane electrodes in a bench-scale zinc electrowinning cell[J]. Hydrometallurgy, 2018, 181: 103-112. DOI:10.1016/j.hydromet.2018.09.003 |
| [17] |
BOISSONNEAU P, BYRNE P. An experimental investigation of bubble-induced free convection in a small electrochemical cell[J]. Journal of Applied Electrochemistry, 2000, 30(7): 767-775. DOI:10.1023/A:1004034807331 |
| [18] |
SCHILLINGS J, DOCHE O, DESEURE J. Modeling of electrochemically generated bubbly flow under buoyancy-driven and forced convection[J]. International Journal of Heat and Mass Transfer, 2015, 85: 292-299. DOI:10.1016/j.ijheatmasstransfer.2015.01.121 |
| [19] |
苏寅彪. 锌电解槽流场数值模拟及其优化[D]. 武汉: 中南大学, 2012. SU Yanbiao. Numerical simulation and optimization for the flow field of the zinc electrowinning cell[D]. Wuhan: Central South University, 2012. |
| [20] |
WANG H, XIA W, YANG W, et al. Improving current efficiency through optimizing electrolyte flow in zinc electrowinning cell[M]. CFD Modeling and Simulation in Materials Processing 2016. Springer, Cham, 2016: 239-245.
|
| [21] |
黎红兵, 杨健, 蒋良兴, 等. 反三明治结构复合多孔Pb合金阳极数值仿真[J]. 中南大学学报(自然科学版), 2020, 51(12): 3357-3366. Li Hongbing, YANG Jian, JIANG Liangxing, et al. Numerical simulation of composite porous Pb alloy anode with inverse sandwich structure[J]. Journal of Central South University (Natural Science Edition), 2020, 51(12): 3357-3366. DOI:10.11817/j.issn.1672-7207.2020.12.010 |
| [22] |
黎红兵, 蒋良兴. 基于电接触模型的锌电积用阳极电场分布仿真计算[J]. 矿冶工程, 2021, 41(1): 90-93, 97. Li Hongbing, JIANG Liangxing. Simulation calculation of electric field distribution of anode for zinc electrowinning based on electric contact model[J]. Mining and Metallurgical Engineering, 2021, 41(1): 90-93, 97. DOI:10.3969/j.issn.0253-6099.2021.01.021 |
| [23] |
冀成庆, 沈明伟, 朱昌洛, 等. 粘土钒精矿中温直接浸出试验研究[J]. 云南冶金, 2014, 43(3): 25-28. JI Chengqing, SHEN Mingwei, ZHU Changluo, et al. Experimental study on direct leaching of clay vanadium concentrate at medium temperature[J]. Yunnan Metallurgy, 2014, 43(3): 25-28. DOI:10.3969/j.issn.1006-0308.2014.03.007 |
| [24] |
GUILLAUME P, LECLERC N, BOULANGER C, et al. I nvestigation of optimal conditions for zinc electrowinning from aqueous sulfuric acid electrolytes[J]. Journal of Applied Electrochemistry, 2007, 37(11): 1237-1243. DOI:10.1007/s10800-007-9377-2 |
| [25] |
ALFANTAZI A M, DREISINGER D B. The role of zinc and sulfuric acid concentrations on zinc electrowinning from industrial sulfate based electrolyte[J]. Journal of Applied Electrochemistry, 2001, 31(6): 641-646. DOI:10.1023/A:1017569400346 |
| [26] |
SU C, ZHANG W, GHALI E, et al. Electrochemical investigation of electrolyte composition and electrolysis parameters during zinc electrowinning[J]. Journal of Applied Electrochemistry, 2017, 47(8): 941-958. DOI:10.1007/s10800-017-1091-0 |
| [27] |
MAHON M, PENG S, ALFANTAZI A. Application and optimisation studies of a zinc electrowinning process simulation[J]. The Canadian Journal of Chemical Engineering, 2014, 92(4): 633-642. DOI:10.1002/cjce.21880 |
| [28] |
MAHON M, ALFANTAZI A. Manganese consumption during zinc electrowinning using a dynamic process simulation[J]. Hydrometallurgy, 2014, 150: 184-191. DOI:10.1016/j.hydromet.2014.10.007 |
| [29] |
KELSALL G H, GUERRA E, LI G, et al. Effects of manganese (Ⅱ) and chloride ions in zinc electrowinning reactors[C]//Proceedings-electrochemical society, 2000, 14: 350-361.
|
| [30] |
朱祖泽, 贺家齐. 现代铜冶金学[M]. 北京: 科学出版社, 2003: 491-581. ZHU Zhuze, HE Jiaqi. Modern Copper Metallurgy[M]. Beijing: Science Press, 2003: 491-581. |
| [31] |
林欣, 陈崇善. 提高铜电解电流效率的生产实践[J]. 铜业工程, 2014, 126(2): 23-25. LING Xin, CHEN Choushan. Production practice of improving current efficiency of copper electrolysis[J]. Copper Industry Engineering, 2014, 126(2): 23-25. DOI:10.3969/j.issn.1009-3842.2014.02.007 |
| [32] |
别良伟. 铜电解精炼过程中的节能措施与实践[J]. 铜业工程, 2011, 107(1): 43-45. BIE Liangwei. Energy-saving measures and practice in the process of copper electrolytic refining[J]. Copper Industry Engineering, 2011, 107(1): 43-45. DOI:10.3969/j.issn.1009-3842.2011.01.011 |
| [33] |
张杰. 电解铜工艺的节能措施及效果[J]. 有色矿冶, 2010, 26(3): 95-96. ZHANG Jie. Energy-saving measures and effects of electrolytic copper process[J]. Nonferrous Mining and Metallurgy, 2010, 26(3): 95-96. DOI:10.3969/j.issn.1007-967X.2010.03.035 |
| [34] |
周玲丽. 电解铜节能新工艺的研究[D]. 上海: 华东理工大学, 2013. ZHOU Liling. Study on the new energy-saving technology of electrolytic copper[D]. Shanghai: East China University of Science and Technology, 2013. |
| [35] |
POHJORANTA A, MENDELSON A, TENNO R. A copper electrolysis cell model including effects of the ohmic potential loss in the cell[J]. Electrochimica Acta, 2010, 55(3): 1001-1012. DOI:10.1016/j.electacta.2009.09.073 |
| [36] |
KÖNIG J, MVHLENHOFF S, ECKERT K, et al. Velocity measurements inside the concentration boundary layer during copper-magneto-electrolysis using a novel laser doppler profile sensor[J]. Electrochimica Acta, 2011, 56(17): 6150-6156. DOI:10.1016/j.electacta.2011.04.034 |
| [37] |
KAWAI S, MIYAZAWA T. CFD modelling and simulation of industrial-scale copper electrorefining process[J]. Minerals Engineering, 2014, 63: 81-90. DOI:10.1016/j.mineng.2014.01.007 |
| [38] |
KAWAI S, OGAWA M, ISHIBASHI K, et al. Transient mass transfer rate of Cu2+ ion caused by copper electrodeposition with alternating electrolytic current[J]. Electrochimica Acta, 2010, 55(12): 3987-3994. DOI:10.1016/j.electacta.2010.02.039 |
| [39] |
Pourahmadi S A A, Talebi S. Hydrodynamic simulation of two phase flow in an industrial electrowinning cell[J]. Modares Mechanical Engineering, 2020, 20(1): 215-225. |
| [40] |
GRAYDON J W, KIRK D W. Suspension codeposition in electrowinning cells: the role of hydrodynamics[J]. The Canadian Journal of Chemical Engineering, 1991, 69(2): 564-570. DOI:10.1002/cjce.5450690223 |
| [41] |
张强, 谢红艳, 张亚晴, 等. CFD技术在湿法冶金中的应用及发展方向[J]. 湿法冶金, 2020, 39(2): 91-95. ZHANG Qiang, XIE Hongyan, ZHANG Yaqing, et al. The application and development direction of CFD technology in hydrometallurgy[J]. Hydrometallurgy, 2020, 39(2): 91-95. DOI:10.13355/j.cnki.sfyj.2020.02.002 |
| [42] |
LEAHY M J, SCHWARZ M P. Experimental validation of a computational fluid dynamics model of copper electrowinning[J]. Metallurgical and Materials Transactions B, 2010, 41(6): 1247-1260. DOI:10.1007/s11663-010-9432-y |
| [43] |
DOCHE O, BAUER F, TARDU S. Direct Numerical Simulation of an electrolyte deposition under a turbulent flow-a first approach[J]. Journal of Electroanalytical Chemistry, 2012, 664: 1-6. DOI:10.1016/j.jelechem.2011.10.003 |
| [44] |
KONISHI Y, TANAKA Y, KONDO Y, et al. Copper dissolution phenomena along a vertical plane anode in CuSO4 solution[J]. Electrochimica Acta, 2001, 46(5): 681-690. DOI:10.1016/S0013-4686(00)00645-9 |
| [45] |
KAWAI S, NISHIKAWA K, FUKUNAKA Y, et al. Numerical simulation of transient natural convection induced by electrochemical reactions confined between vertical plane Cu electrodes[J]. Electrochimica Acta, 2007, 53(1): 257-264. DOI:10.1016/j.electacta.2007.06.011 |
| [46] |
YANG X, ECKERT K, SEIDEL K, et al. The start-up of natural convection during copper electrolysis in the presence of an opposing Lorentz force[J]. Electrochimica Acta, 2008, 54(2): 352-359. DOI:10.1016/j.electacta.2008.07.074 |
| [47] |
LEAHY M J, SCHWARZ M P. Modeling natural convection in copper electrorefining: describing turbulence behavior for industrial-sized systems[J]. Metallurgical and Materials Transactions B, 2011, 42(4): 875-890. DOI:10.1007/s11663-011-9504-7 |
| [48] |
KEMMINGER A, LUDWIG A. Modelling the electrolyte flow in a full-scale copper electrorefining tankhouse cell[C]//Proceedings of European Metallurgical Conference EMC, 2013, 2: 795-806.
|
| [49] |
MANDIN P, CENSE J M, GEORGES B, et al. Prediction of the electrodeposition process behavior with the gravity or acceleration value at continuous and discrete scale[J]. Electrochimica Acta, 2007, 53(1): 233-244. DOI:10.1016/j.electacta.2007.01.044 |
| [50] |
MANDIN P, CENSE J M, PICARD G, et al. Simplified kinetic modelling and numerical simulation of a metal oxide chemical bath electro deposition process at a rotating electrode[J]. Electrochimica Acta, 2006, 52(3): 1296-1308. DOI:10.1016/j.electacta.2006.07.031 |
| [51] |
MANDIN P, CENSE J M, FABIAN C, et al. Electrodeposition process modeling using continuous and discrete scales[J]. Computers & Chemical Engineering, 2007, 31(8): 980-992. DOI:10.1016/j.compchemeng.2006.10.018 |
| [52] |
MANDIN P, WVTHRICH R, ROUSTAN H. Electrochemical engineering modelling of the electrodes kinetic properties during two-phase sustainable electrolysis[M]. Computer Aided Chemical Engineering. Elsevier, 2009, 27: 435-440.
|
| [53] |
KIM K R, CHOI S Y, PAEK S, et al. Electrochemical hydrodynamics modeling approach for a copper electrowinning cell[J]. International Journal of Electrochemical Science, 2013, 8(11): 12333-12347. |
| [54] |
ALLEN J B, LARRY R F. Electrochemical methods fundamentals and applications[M]. John Wiley & Sons, 2001.
|
| [55] |
WERNER J M, ZENG W, FREE M L, et al. Modeling and validation of local electrowinning electrode current density using two phase flow and nernst-planck equations[J]. Journal of The Electrochemical Society, 2018, 165(5): E190. DOI:10.1149/2.0581805jes |
 2021, Vol. 29
2021, Vol. 29