2. 哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001
2. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
复合材料是人们运用先进的材料制备技术将不同性质的材料组份优化组合而成的新材料[1-3]。先进复合材料的三维编织预成型体的设计和制造因其出色的力学性能而备受关注[4-7]。三维编织复合材料除了具有常规复合材料所具备的高比刚度和比强度、良好的耐腐蚀性等优点外,还具有更好的抗冲击性,耐疲劳性,更高的损伤容限,且无常规铺层结构层间结合力弱的问题[8-12]。虽然编织技术为复合材料提供了一种理想的预成型工艺,但编织物的结构受到编织设备和编织工艺的制约[13]。
二维织物被广泛应用于复合材料层合板的制造中,由于织物层与层之间通过基体胶结在一起,并无纤维连接,在受到剪切应力和交变应力时层间结合力弱,容易发生分层或者开裂[14-15]。三维编织技术,是由两个或两个以上相互缠绕的纱线系统,通过整体成型的方式得到立体编织物的方法[16]。该技术很好地改善了预制体厚度方向的承载性能,是解决分层问题的有效方法之一。
目前三维编织设备主要分为笛卡尔式纵横编织机和旋转式三维编织机。纵横式编织机常采用手工编织方式,旋转式三维编织机的拨盘一般为四角拨盘,能够携带的纱锭数量有限,数字化程度和灵活性不足。此外,传统编织机功能单一,通常一套编织设备只能编织一种细观织物预制体。加拿大温哥华英属哥伦比亚大学高级纤维材料实验室(AFML)和德国亚琛工业大学纺织技术研究所(ITA),合作开发了一种拨盘为六齿型的新型三维编织机[17]。该原理设计的三维编织设备灵活度高,适合各种不同细观结构的编织,结构紧凑,是未来三维编织的发展方向之一。目前关于六齿型编织原理样机的整体控制原理和结构设计的研究报道较少,特别是针对可以连续铺放轴纱、三维五向水平放纱的六齿型三维编织原理样机的研究尚鲜有报道。因此,本文研制了一种在现有六齿型三维编织的基础上可以连续铺放轴纱的高灵活度编织原理样机及其编织工艺,通过建立纱线的空间运动坐标系分析纱线的运动,同时设计了恒张力水平携纱器,并通过有限元模拟验证其安全性。使用850D的聚丙烯纤维进行编织实验,对编织结构仿真结果进行验证。
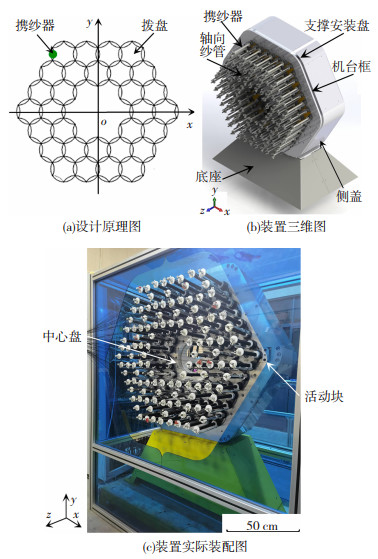
1 原理样机的搭建根据六角形编织工艺,采用六角形拨盘外接圆紧密排布的基本原理搭建原理样机[17]。与传统四角形拨盘相比,单位携带的纱线更多,可以提高编织复合材料增强纤维的体积分数。设计原理图如图 1(a)所示,六齿型三维编织原理样机设置两层滑块驱动层,每层滑块驱动层包含6n(n≥2)个六齿型拨盘,最多可容纳120个携纱器,30个拨盘和轴向纱管。六齿型拨盘两两相邻、围绕中心盘呈环形安装在运行槽内。运行槽由机台框、活动块、中心盘和支撑安装盘构成。
|
图 1 新型六角三维编织原理样机实机 Fig.1 Prototype of the new type of hexagonal 3Dbraiding prototype machine: (a) schematic of the design; (b) 3D diagram of the machine; (c) actual assembly of the machine |
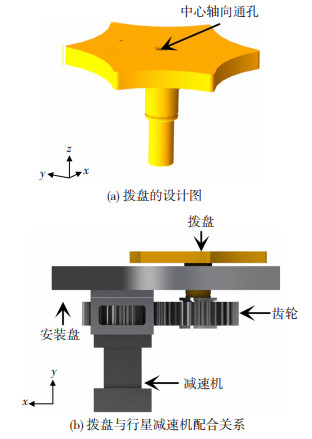
为了实现轴纱连续铺放,本文设计了可安装轴向纱管的中心通孔结构拨盘,三维结构如图 2(a)所示。采用传动比为1∶1的空心轴直齿圆柱齿轮啮合的传动方式以减少传动误差和回转间隙。根据齿轮几何尺寸,齿面弯曲强度和经验公式确定齿轮模数m[18]。
|
图 2 拨盘设计与行星减速机装配图 Fig.2 Design of the horn-gear and assembly of the horn-gear and the planetary reducer: (a)design of the horn-gear; (b)assembly of the horn-gear and the planetary reducer |
齿轮几何尺寸计算公式为
| $ m=\frac{d}{z} $ | (1) |
| $ b=K_{\mathrm{c}} m $ | (2) |
直齿齿面接触疲劳极限参数
| $ a \geqslant 483(\mu \pm 1) \sqrt[3]{\frac{K T_{1}}{\phi_{a} \sigma_{\mathrm{HP}}^{2} u}} $ | (3) |
| $ d_{1} \geqslant 766 \sqrt[3]{\frac{K T_{1}}{\phi_{d} \sigma_{\mathrm{HP}}^{2}} \frac{u \pm 1}{u}} $ | (4) |
经验公式
| $ m=(0.007 \sim 0.02) a $ | (5) |
式中:d为分度圆直径,mm;b为齿宽,mm;Kc为齿宽系数;K为载荷系数;σHP为接触应力,MPa;u为初定齿数比;a为中心距,mm;ϕa为对中心距的齿宽系数;ϕd为对分度圆直径的齿宽系数。拨盘几何型貌与行星减速机的配合如图 2(b)所示。电机通过行星减速机带动齿轮转动,从而带动拨盘的转动。
1.2 携纱器载体设计原理样机的关键部件是携纱器载体,携纱器由纱架与滑块组成。滑块的尺寸要控制在一定的范围内以减小回转间隙,设滑块公称直径(滑槽宽度)为D,则它们的配合方式可取为DHx/hy或DHx/gy、DHx/fy及DHx/ey等,x,y为精度等级[19]。
选用聚四氟乙烯材料制造表面粗糙度为N5的导眼,以减少纱线的损伤或丝束断裂。为保证纱线恒张力出纱,需要计算储纱量ΔL。以支撑盘中心为原点O,建立如图 3所示的纱线运动坐标系Oxyz。纱线距原点O最远点为Ymax(x1, 0, z1),最近点为Ymin(x2, 0, z2),编织芯轴圆周上的点为Bp1(x3, y, z3)和Bp2(x4, y, z4), 且(y > 0)。

|
图 3 纱线运动坐标系 Fig.3 Coordinate system of yarn motion |
储纱量(ΔL)为
| $ \Delta L=\left|\overrightarrow{Y_{\max } B_{p 2}}\right|-\left|\overrightarrow{Y_{\min } B_{p 1}}\right| $ | (6) |
即
| $ \begin{gathered} \Delta L=\sqrt{\left(x_{1}-x_{4}\right)^{2}+y^{2}+\left(z_{1}-z_{4}\right)^{2}}- \\ \sqrt{\left(x_{2}-x_{3}\right)^{2}+y^{2}+\left(z_{2}-z_{3}\right)^{2}} \end{gathered} $ | (7) |
Bp1和Bp2为芯轴圆周上的点,即|x3|=|z3|,|x4|=|z4|,纱线Bp1Ymin与中心轴的夹角(αmin)为
| $ \alpha_{\min }=\tan ^{-1} \frac{\sqrt{x_{2}^{2}+z_{2}^{2}}-\left|x_{3}\right| \sqrt{2}}{|y|} $ | (8) |
同理可推导出编织机上的纱线与轴向的夹角,即编织角(αi)为
| $ \alpha_{i}=\tan ^{-1} \frac{\sqrt{x_{i}^{2}+z_{i}^{2}}-\left|x_{j}\right| \sqrt{2}}{|y|}(i>0, j>0) $ | (9) |
式中: xi,yi为纱线的出纱点的坐标值;xj为芯模上的点的x轴坐标值。
根据储纱量ΔL设计的携纱器载体如图 4所示。

|
图 4 携纱器的设计 Fig.4 Design of the yarn carrier: (a) 3D diagram of the yarn carrier; (b) picture of the actual yarn carrier |
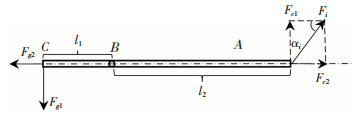
为确保携纱器载体使用的安全性,结合式(9)对携纱器进行受力分析,建立如图 5所示的携纱器受力分析简图。图 5中的A点为携纱器与纱线的受力点,B点为携纱器与拨盘的接触点,C点为携纱器对拨盘的作用力点。
|
图 5 携纱器受力简图 Fig.5 Force on the yarn carrier |
从图 5可知,对纱线的作用力Fi可分解为对携纱器的压力Fc1和拉力Fc2,则单个携纱器对拨盘的作用力(Fg1)为
| $ F_{g 1}=\frac{F_{i} \sin \alpha_{i} l_{2}}{l_{1}} $ | (10) |
式中:l1为携纱器顶端到拨盘面的距离;l2为拨盘到携纱器底端的的距离。
Fg2为拨盘防止携纱器脱出力,Fg1与拨盘所受到的正压力FN相等,从而可以求得编织机在出纱阶段所受到的总正压力(FNs)为
| $ F_{N s}=\frac{l_{2} \sum\nolimits_{i=1}^{120} \sin \alpha_{i}}{l_{1}} $ | (11) |
对携纱器进行静应力仿真分析,根据图 5建立锭杆与滑块的有限元模型。网格化后锭杆共有单元数81 678、节点数141 698,求解时间14 s,Fi=5 N,Fc1=4.3 N;网格化后滑块共有单元数147 940、节点数228 034,求解时间22 s,Fg1=18.9 N,滑块内部扭簧等效为FH=1.5 N,边界条件均为模型边界。由图 6(a)可以看出,在携纱器工作时,锭杆的最大应力为81 MPa,集中在截面突变处,小于6061-T4铝合金的屈服应力。滑块的主要受力集中在拨盘接触块处,如图 6(b)所示。滑块所受最大应力为0.107 3 MPa,远小于尼龙材料的屈服强度,因此满足强度要求。

|
图 6 携纱器静应力有限元仿真 Fig.6 Finite element simulation of static stress of yarn carrier |
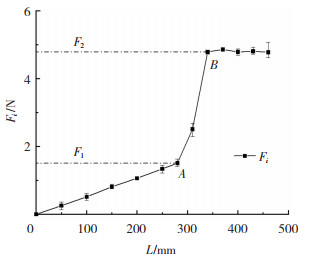
使用NK-50指针式推拉计对单个携纱器进行牵引力与纱线伸长量测试。图 7为外部牵引力与纱线伸长量的Fi-L曲线,可以观察到,力在几个特征点上发生了变化,这些特征点依次用A、B标记。在A点前,拉力Fi呈线性增长,这是由于携纱器内置了保证纱线具有一定储纱量的拉簧处于弹性变形阶段。AB阶段Fi的值显著提升,此时拉簧顶开卡扣后开始出纱。B点后即为出纱阶段,拉力波动较小,保持恒张力出纱。
|
图 7 外部牵引力(Fi)与纱线伸长量(L)曲线 Fig.7 Curve of take-off force and yarn elongation Fi-L |
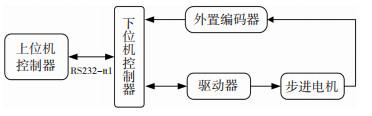
本原理样机的控制系统包括通过STM32芯片搭建下位机硬件控制电路和采用C语言开发的上位机软件程序。下位机主要负责向驱动器发指令、采集编码器以及与上位机通信。上位机软件负责顶层的逻辑控制、运动规划以及与下位机通信。上下位机之间采用RS232-ttl串口通信。控制系统总体方案示意图如图 8所示。
|
图 8 控制系统总体方案示意图 Fig.8 Schematic of the overall control system |
编织控制软件是应用Visual Studio,基于Windows 7以上64位操作系统开发的。软件主要包括控制任务,传感器数据采集任务,通信任务,与信号监测任务。通过编织控制、编写编织过程等功能和操作实现对编织机的控制,对每个拨盘的回零传感器进行信号采集,对驱动器返回的脉冲信号进行数据处理,保证设备的正常运行。软件的程序控制逻辑如图 9所示。

|
图 9 软件设计总逻辑框图 Fig.9 Logic blocks of software design |
通过在上机位发送指令信号控制电机的运行,根据串口获得的每个电机的转动角度(60°,120°,180°)来计算每个电机脉冲的时间间隔,并根据累计的脉冲数计算和消除累计误差,程序如下。
void Timer_Init()//8个定时器初始化
{
......
}
void Motor operation()//电机运行
{
......
incubator00.motor_1_add_time=0;//清零每个电机需要发送脉冲数(转动角度相关)
......
incubator00.motor_1_sec=0;//清零脉冲间隔(转动速度相关)
......
get_usart(); //获取串口数据
......
incubator00.motor_1_add_time=incubator00.com_data[1]*STEP+motor_sec_180; //计算脉冲数量+累计误差消除脉冲数量
......
incubator00.motor_1_sec=incubator00.com_data[9]*TIME; //计算时间间隔,即定时器间隔
.....
TIM_Cmd(TIM1, ENABLE); //启动定时器,并输出脉冲
}
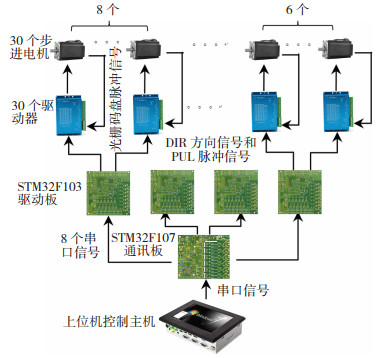
2.2 系统控制硬件设计通过4块驱动控制板对30个电机进行分组控制。上位机控制主机发送编织工艺的串口信号,由串口通讯板将信号分成4路传输给底层驱动板,驱动板将输入的串口信号计算转换为可被驱动器识别的DIR方向信号和PUL脉冲信号。电机后置编码器反馈光栅信号给驱动器,保护设备的同时保证编织工艺的精确性。系统控制硬件连接框图如图 10所示。
|
图 10 系统控制硬件连接框图 Fig.10 Block diagram of system control hardware connection |
使用Altium软件进行PCB板设计,PCB板设计原理图如图 11(a)所示。控制功能分为通讯数据处理和电机驱动,每块电路板使用2块STM32系列单片机作为主控芯片,均为LQFP-144封装,负责中断电机的脉冲信号输出、接受串口控制信号和运行数据处理等,并将控制数据发送至STM32F107。使用PC817B光耦芯片作为输入输出的隔离,以防止电泳等造成的电路板损毁。PCB板的对外输出采用ULN2003三极管和PC817光耦等。利用ULN2003提升单片机IO口的输出能力,以便驱动PC817光耦,为PCB板的功能扩展做预留。

|
图 11 PCB板 Fig.11 PCB circuit board: (a) schematic of PCB circuit board; (b) picture of the actual circuit board |
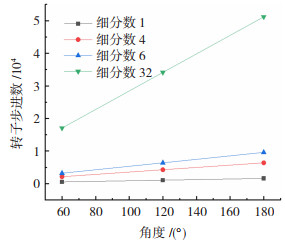
选用57系两相四线步进电机,扭矩为2.2 N·m,步进角为1.8°,细分数为1,4,6,32。高细分数可提高步进电机的定位精度,减少失步[20]。当细分数为32时,其控制角最小为0.056 25°(1.8°/32=0.056 25°),经过16∶1的行星减速机,其理论步进角的控制精度为0.003 515 625°(1.8°/32/16=0.003 515 625°)。拨盘转动角度与电机转子步进数的关系如图 12所示。
|
图 12 拨盘转动角度与转子步进数的关系图 Fig.12 Curves of rotation angle of horn-gear and step number of rotor |
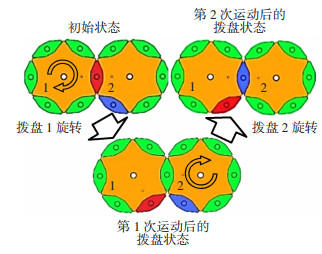
通过每个相邻拨盘的顺逆时针运动带动携纱器运动,使纱线两两交织并通过外部牵引实现纱线的编织工艺。在编织过程中,相邻的拨盘不可同时旋转且转动的角度是60°的整数倍,图 13为编织工艺原理示意图。图 14为原理样机进行编织实验的现场图。
|
图 13 六角形编织工艺原理示意图 Fig.13 Schematic of 3D braiding process of hexagonal horn-gears |

|
图 14 原理样机进行编织实验 Fig.14 Braiding experiment on prototype machine |
纱线运动路径是纱线围绕芯模螺旋向上,其路径的形成规律由携纱器旋转1周的速度和机器人运行的速度决定, 但在实际编织过程中, 单一纱线运动路径为多圈或不足一圈。为表达在编织异径结构的预制体时,携纱器的转速与外部牵引设备运动速度v的关系,建立如图 15所示的纱线实际运动路径模型。通过图 15(b)中纱线路径的弧长x(mm)建立等式,则外部牵引设备运行速度v(mm/s)与携纱器转速的关系为
| $ v=\frac{2 {\rm{ \mathsf{ π} }} v_{\mathrm{r}} R_{i}}{\tan \alpha_{i}} $ | (12) |

|
图 15 纱线运动模型 Fig.15 Movement model of a single yarn |
式中:Ri为芯模的实时半径,mm;vr为携纱器在设备上运行一圈的速度,r/s;αi为式(9)中编织角,单位(°)。
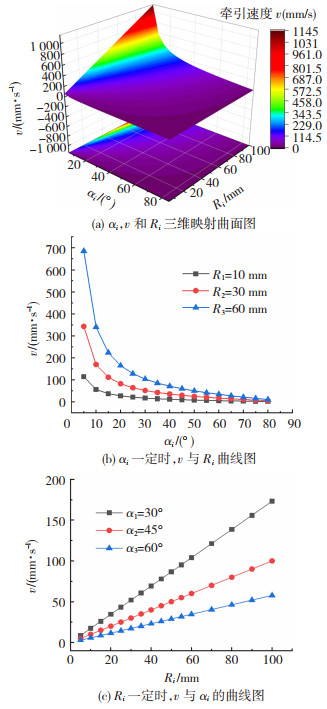
根据式(12),当2πvr值为定值1时,编织角αi,外部牵引速度v和芯模半径Ri的关系如图 16(a)所示。从图 16(b)和(c)可以发现,当Ri为定值时,v与αi呈近似线性反比关系;当αi为定值时,v与Ri呈线性增大关系。即编织异径结构件时通过瞬时芯模半径Ri与编织角αi可确定外部牵引的实时速度v。
|
图 16 αi,v和Ri关系曲线 Fig.16 Curves of αi, v, and Ri: (a) 3D mapping surface diagram of αi, v, and Ri; (b) curve of v and Ri with constant αi; (c) curve of v and αi with constant Ri |
基于携纱器的运动轨迹模拟生成的纱线的运动轨迹,首先需要计算出原始纺线的轨迹。携纱器的运动是一个位于平面上的周期运动,携纱器Ai的运动轨迹设为(Xi(t), Yi (t)),其中t是时间参数。纱线上升的高度用Z(t)表示,则携纱器Ai生成的纱线的空间轨迹参数方程为
| $ (x(t), y(t), z(t))=\left(X_{i}(t), Y_{i}(t), Z(t)\right) $ | (13) |
芯模的表面是一个旋转曲面。设芯模底面的中心为笛卡尔坐标系x-y-z的原点,芯模的轴线与坐标系的z轴重合。芯模表面坐标(u, v, w)可以用如下的参数方程表示。
| $ \left\{\begin{array}{l} u=R(z) \cos \alpha_{i} \\ v=R(z) \sin \alpha_{i}, \alpha_{i} \in[0, 2 {\rm{ \mathsf{ π} }}], z \in[0, H] \\ w=z \end{array}\right. $ | (14) |
其中,H表示芯模的高度,R(z)是柱芯的半径Ri关于高度z的函数,由式(12)推导得到
| $ R_{i}=\frac{\tan \alpha_{i} L}{2 {\rm{ \mathsf{ π} }} v_{\mathrm{r}} t} $ | (15) |
式中:L即为高度|z|,mm;t为运动时间,mm。
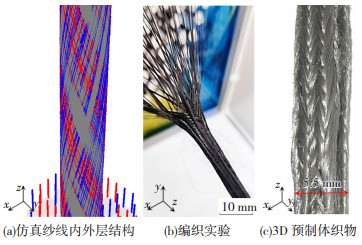
将纱线空间曲线函数投影到芯模函数上得到纱线的运动轨迹曲线。利用纱线空间曲线函数,模拟编织机在装满120个纱锭的情况下进行纱线路径模拟,如图 17(a)所示,可以看到,纱线均为交织缠绕类且无驻留纺线,显示了良好的编织结构。在红蓝线交织位置出现红球则代表该点红线在外层,蓝球表示蓝线在外层。通过原理样机以850D聚丙烯纤维为材料进行多层三维编织实验,如图 17(b),(c)所示。研究发现,编织物的编织结构与模拟编织结构一致,可以验证模拟结果的准确性。
|
图 17 多层三维编织织物结构 Fig.17 Multilayer 3D braided structure: (a)simulation results of braided structure; (b) braiding experiment; (c) 3D braided preforms |
该原理样机不仅可以编织常规等截面结构,如圆形、方形、六角形等截面结构,还可实现变截面复杂三维结构的编织,如表 1所示。几种典型的编织截面形状如表 2所示。与传统的三维编织机相比,该原理样机既可用于编织多层三维编织结构,也可以设计简单的二维编织结构。此外在编织过程中加入芯模,可以一次成型所需的异径结构零部件。
| 表 1 新型三维编织原理样机可编织的截面形状 Table 1 Cross-sectional shapes that can be braided by the new type of 3D braiding prototype machine |
| 表 2 编织典型截面形状 Table 2 Typical cross-sectional braided shapes |
本文从机械结构设计、控制系统设计构建一种可连续铺放轴纱的数字化多轴向水平放纱三维编织原理样机,并研究其编织工艺。
1) 原理样机最多可容纳120个运动携纱器和30个固定轴向纱管。通过建立纱线空间运动坐标系计算储纱量,构建了携纱器的有限元分析模型,结果表明携纱器工作时,锭杆最大应力为81 MPa集中在截面突变处,滑块最大应力为0.107 3 MPa集中在拨盘接触块处。
2) 采用Visual Studio,设计开发了基于Windows 7以上64位操作系统的上位机实时控制程序。以STM32微控制器设计了原理样机的下位机硬件控制电路。理论步进角的控制精度为0.003 515 625°的步进电机,最大程度的保证了编织结构的灵活性和精确度。
3) 编织预制体通过拨盘的旋转与外部牵引设备的配合进行三维编织成型,根据纱线运动路径建立纱线运动模型。结果表明,当携纱器运动速度一定时,不同的外部牵引速度影响编织预制体的编织角度与截面结构。建立纱线空间曲线参数方程模拟纱线的运动轨迹,通过实验对比,验证本原理样机编织多层织物结构的可行性和仿真结果的准确性。
此原理样机数字化程度高,适用于制造长构件、高可靠性不同尺寸的编织体,可以实现三维五向管状预制体一体编织,减少加工时间,对提升航空航天关键复合材料的成型具有重要价值。
| [1] |
韩新宇. 基于有限元分析方法的储罐复合材料涂层修复评估技术[J]. 科技创新导报, 2019, 16(22): 103-104. HAN Xinyu. Evaluation technology of composite coating repair for storage tank based on finite element analysis method[J]. Science and Technology Innovation Herald, 2019, 16(22): 103-104. |
| [2] |
TOOZANDEHJANI M, KAMARUDIN N, DASHTIZADEH Z, et al. Conventional and advanced composites in aerospace industry: Technologies revisited[J]. American Journal of Aerospace Engineering, 2018, 5(1): 9-15. DOI:10.11648/j.ajae.20180501.12 |
| [3] |
MONALISA D, SASMITA S, PARHI D R. Composite materials and their damage detection using AI techniques for aerospace application: A brief review[J]. Materials Today: Proceedings, 2020, 11: 005. DOI:10.1016/j.matpr.2020.11.005 |
| [4] |
高彦涛. 六角形编织工艺、结构和性能及编织结构复合材料整合设计[D]. 上海: 东华大学, 2013. GAO Yantao. Process, structures and properties of hexagonal braiding and integrated design of braided structural composites[D]. Shanghai: Donghua University, 2013. |
| [5] |
ZUO Hongmei, LI Diansen, JIANG Lei. Experimental study on compressive fatigue behavior and failure mechanism of 3D five-directional braided composites[J]. Composites Part A, 2020, 139. DOI:10.1016/j.compositesa.2020.106097 |
| [6] |
MEI Haiyang, HAN Zhenyu, LIANG Shuangqiong, et al. Process modeling of 3D hexagonal braids[J]. Composite Structures, 2020, 252: 112679. DOI:10.1016/j.compstruct.2020.112679 |
| [7] |
GE Jingran, HE Chunwang, LIANG Ju, et al. A coupled elastic-plastic damage model for the mechanical behavior of three-dimensional (3D) braided composites[J]. Composites Science and Technology, 2018, 157: 86-98. DOI:10.1016/j.compscitech.2018.01.027 |
| [8] |
WANG Ya, LIU Zhenguo, WEI Yuchen, et al. Novel processing technology and mesoscopic geometric modeling of a new three-dimensional (3D) braided composite and the study on its longitudinal mechanical properties[J]. Composite Structures, 2020, 251: 112525. DOI:10.1016/j.comp-struct.2020.112525 |
| [9] |
HAO Wenfeng, HUANG Zhen, XU Yezhuang, et al. Acoustic emission characterization of tensile damage in 3D braiding composite shafts[J]. Polymer Testing, 2020, 81: 106176. DOI:10.1016/j.polymertesting.2019.106176 |
| [10] |
杨彩云, 马景祥, 马立, 等. 3D机织复合材料多向接头有限元分析[J]. 材料科学与工艺, 2015, 23(6): 24-28. YANG Caiyun, MA Jingxiang, MA Li, et al. Experimental study on influence of fabric structureon mechanical properties of composites[J]. Material Science and Technology, 2015, 23(6): 24-28. DOI:10.11951/j.issn.1005-0299.20150605 |
| [11] |
ZHANG Di, ZHENG Xitao, WANG Zhibang, et al. Effects of braiding architectures on damage resistance and damage tolerance behaviors of 3D braided composites[J]. Composite Structures, 2020, 232: 111565. DOI:10.1016/j.compstruct.2019.111565 |
| [12] |
ZHOU Haili, LI Chao, ZHANG Liquan, et al. Micro-XCT analysis of damage mechanisms in 3D circular braided composite tubes under transverse impact[J]. Composites Science and Technology, 2018, 155: 91-99. DOI:10.1016/j.compscitech.2017.11.025 |
| [13] |
SCHREIBER F, THEELEN K, SCHULTE S E, et al. 3D-hexagonal braiding: Possibilities in near-net shape preform production for lightweight and medical applications[C]//18th International Conference on Composite Materials. Jeju Island, Korea: ICCM, 2011.
|
| [14] |
刘静, 王益轩, 王永强, 等. 三维编织机虚拟样机研究[J]. 产业用纺织品, 2017, 35(12): 21-27. LIU Jing, WANG Yixuan, WANG Yongqiang, et al. Study on the virtual prototype of 3D braiding machines[J]. Technical Textiles, 2017, 35(12): 21-27. |
| [15] |
谭伟, 那景新, 任俊铭, 等. 高温环境下碳纤维增强树脂复合材料的层间力学性能老化行为与失效预测[J]. 复合材料学报, 2020, 37(4): 125-134. TAN Wei, NA Jingxin, REN Junming, et al. Aging behavior and failure prediction of interlaminar mechanical properties of carbon fiber reinforced polymer composite at high temperature[J]. Acta Materiae Compositae Sinica, 2020, 37(4): 125-134. DOI:10.13801/j.cnki.fhclxb.20190619.002 |
| [16] |
李政宁, 陈革, KO F. 三维编织工艺及机械的研究现状与趋势[J]. 玻璃钢/复合材料, 2018, 5: 109-115. LI Zhengning, CHEN Ge, KO F. The development and tendency of 3D braiding technology and machinery[J]. Composites Science and Engineering, 2018, 5: 109-115. DOI: CNKI:SUN:BLGF.0.2018-05-018 |
| [17] |
SCHREIBER F, KO F, YANG H J, et al. Novel three-dimensional braiding approach and its products[C]//17th International Conference on Composite Materials. Edinburgh: IOM Communications, 2009.
|
| [18] |
成大先. 机械设计手册[M]. 第5版. 北京: 化学工业出版社, 2010: 889-910. CHENG Daxian. Handbook of mechanicaldesign[M]. 5th ed. Beijing: Chemical Industry Press, 2010: 889-910. |
| [19] |
朱建勋, 蒋云, 陆晓华, 等. 三维编织机锭子, 轨道及锭槽结构尺寸的选择[J]. 宇航材料工艺, 1998, 28(3): 49-53. ZHU Jianxun, JIANG Yun, LU Xiaohua, et al. A selecting of the structure and dimension of carries, tracks and columns in 3D braiding machine[J]. Aerospace Materials & Technology, 1998, 28(3): 49-53 DOI: CNKI:SUN:YHCG.0.1998-03-014 |
| [20] |
伍艳雄. 步进电机细分驱动控制研究[D]. 恩施: 湖北民族大学, 2019. WU Yanxiong. Research of stepping motor subdivision drivecontrol[D]. Enshi: Hubei Minzu University, 2019. |
 2021, Vol. 29
2021, Vol. 29