随着科技的发展,机械装备向大型化、轻量化方向发展,对构件性能提出更高要求[1],单一金属材料已不能满足工程的使用要求,而异种钢焊接结构件由于具有不同材料的优异性能,且具有成本优势,受到重视并在石油化工[2]、航空航天、电站锅炉[3]、工程机械等行业的装备和构件中得到广泛应用[4-6]。
异种钢焊接时,由于焊缝两侧材料热导率、比热容、熔点等热物理性能的差异[7],以及焊缝两侧材料导磁性能的差异造成焊接电弧的磁偏吹现象,致使在焊接过程中焊缝两侧材料受到电弧不均匀的加热和冷却[8],导致焊缝处产生较大的集中内应力[9-10],以及裂纹等焊接缺陷[11-12]。近年来,304L不锈钢和Q235低碳钢异种钢焊接结构件开始用于工业生产,但由于304L不锈钢热导率远大于Q235低碳钢,且304L不锈钢比热容低于Q235低碳钢。因此,为获得良好的焊缝熔透质量,在焊接过程中,304L不锈钢侧比Q235低碳钢侧应给予更多的电弧热输入,这也意味着需要对焊接电弧热进行必要的能量分配和干预。脉冲GTAW焊接作为在工业生产中广泛使用的一种焊接方法,具有电弧稳定[13],热输入小,便于精确控制电弧能量分布,能够对可焊性较差的金属进行焊接[14]。采用脉冲GTAW进行异种钢的焊接,可以更为精确地进行电弧能量的控制,获得好的焊接质量。
针对Q235低碳钢和304L不锈钢异种金属GTAW角焊,建立了直流脉冲的二维瞬态电弧模型,采用数值模拟与实验相结合的方式分析了异种钢焊接电弧偏转机理,焊接电流对磁偏吹的影响规律。获得了异种钢两侧电弧热流密度在工件表面的分布,以及不同焊枪角度对两侧热流密度的影响规律。建立了焊接角度影响两侧能量分配的回归方程,并对不同焊枪偏转角度下电弧热输入对304L不锈钢和Q235低碳钢角焊缝焊接结果的影响进行焊接试验验证。研究结果可为异种钢角焊接两侧金属能量调控提供一定的技术支持。
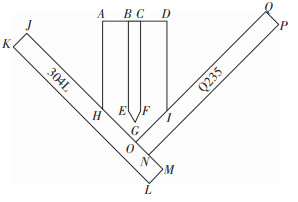
1 数学模型 1.1 基本假设电弧的数值计算模型如图 1所示,在计算时对电弧做出如下假设。
|
图 1 模型求解域 Fig.1 Schematic of calculation domain |
1) 假定氩气、等离子体均处于标准大气压下且不可压缩[15]。
2) 假定电弧为光学薄膜介质, 且处于局部热力学平衡(LTE)下[16]。
3) 忽略电弧粘性效应导致的热损失和重力影响。
4) 氩气和电弧等离子体的流动状态为层流[17]。
1.2 控制方程基于以上假设,得出下列模型控制方程。
质量守恒方程
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot \rho \boldsymbol{v}=0 $ | (1) |
动量守恒方程
| $ \left(\frac{\partial v}{\partial t}+\boldsymbol{v} \cdot \nabla \boldsymbol{v}\right)=-\nabla P+\nabla \cdot \tau+j \times B+\rho g $ | (2) |
能量守恒方程
| $ \rho C_{P}\left(\frac{\partial T}{\partial t}+\boldsymbol{v} \cdot \nabla T\right)=\nabla \cdot(k \nabla T)+S $ | (3) |
能量守恒方程源项S的表达式为
| $ S=j \times E+\frac{5 k_{\mathrm{B}}}{2 e} j \cdot \nabla T-4 {\rm{ \mathsf{ π} }} \varepsilon_{\mathrm{N}} $ | (4) |
式中:ρ为等离子体的密度;v为速度矢量;T为温度;CP为定压比热;kB为玻尔兹曼常数,值为5.670 373×10-8 W/(m2·k4);σ为电导率;j为电流密度;e为电子电量;εN为氩气随温度变化的净排放系数。
式(4)中三项分别表示电弧焦耳热、电子传输焓以及电弧辐射热损失。
电流连续性方程
| $ \nabla \cdot\left(\sigma \nabla V+\sigma \frac{\partial A}{\partial t}\right)=0 $ | (5) |
推导出电场及电流密度方程为
| $ E=-\nabla V-\frac{\partial A}{\partial t} $ | (6) |
| $ j=-\sigma \nabla V-\sigma \frac{\partial A}{\partial t} $ | (7) |
磁矢量方程
| $ \sigma \frac{\partial A}{\partial t}+\nabla\left(\frac{1}{\mu_{0}} \nabla \times A\right)+\sigma \nabla V=0 $ | (8) |
磁感应强度为
| $ B=\nabla \times A $ | (9) |
式中:j为电流密度;B为磁感应强度;μ0为真空磁导率;V为电势;A为磁矢势。
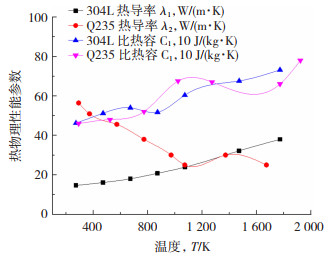
1.3 计算区域及边界条件瞬态电弧模型的计算区域见图 1,其中,JKLM区域为Q235低碳钢计算域,PQON为304L,其中,不锈钢计算域,材料计算域大小为50 mm×4 mm,图 2为材料的热物理性能参数;图 1中BCFGE五边形区域为钨针计算域,钨针直径为2.4 mm,钨针尖端角度为60°,模型中为了计算方便,并使结果能够更快收敛,将钨针尖端简化为直径0.2 mm的圆弧,电弧弧长为3 mm。
|
图 2 材料热物理性能参数 Fig.2 Thermophysical properties of materials |
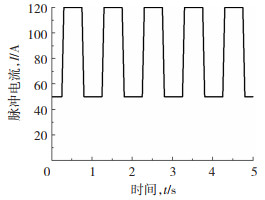
图 1中BC为电极阴极,本模型计算峰值电流为直流脉冲电流,基值电流I0=50 A, 峰值电流Ip=120 A,电流频率f=1 Hz,占空比为0.5。模型计算时长为3 s。电流脉冲图形如图 3所示。
|
图 3 电流脉冲图 Fig.3 Current pulse diagram |
图 1中AB和CD为氩气入口,气体流量为18 L/min,相对应的气体流速在表 1中表示为ug。HO和IO为氩气出口。该模型的其他边界条件设定如表 1所示,表中Rc为钨针半径。
| 表 1 边界条件 Table 1 Boundary conditions |
采用COMSOL Multiphysics多物理场仿真软件构建电弧瞬态模型,包括电场、磁场、层流以及流体传热多个物理场,对多个物理场进行统一全耦合求解。使用COMSOL Multiphysics软件的感应/直流耦合放电多物理场接口:电流接口计算电弧的电流和电势分布,使用标量电势作为因变量,基于欧姆定律求解电流守恒方程;磁场接口计算电弧磁场和感应电流分布,求解使用矢量磁势的麦克斯韦方程;流体传热接口计算电弧的传导传热、对流传热和辐射传热;层流接口求解电弧的能量、质量和动量守恒。通过构建瞬态电弧模型的全耦合偏微分方程组,使用有限元法(FEM)对该偏微分方程组进行空间坐标(x、y)的离散化处理。经离散化处理后得到该瞬态模型的非线性方程组,使用牛顿法对该方程组进行迭代求解。设置最大迭代次数为100次,初始衰减因子为0.01,最小衰减因子为10-6,相对容差设置为0.001。
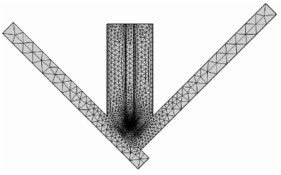
采用COMSOL Multiphysics多物理场仿真软件自带网格划分工具进行网格划分。对模型求解域使用自由三角形网格进行划分,等离子区域以及近焊缝区细密,其他区域网格稀疏,从而保证模型计算精度和节省计算时间。划分自由三角形网格3 218个,求解自由度数48 054。网格划分如图 4所示。
|
图 4 求解域网格划分 Fig.4 Calculation domain mesh division |
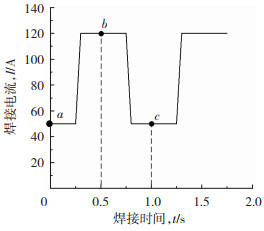
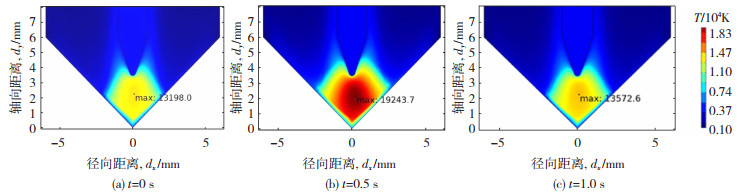
图 5为焊接电流与焊接时间的关系曲线。图 6为图 5中不同焊接时刻的电弧温度场。图 6(a)为t=0 s时基值电流(Ib)为50 A时的温度场,电弧最高温度(T)为13 198 K, 位于钨针下方1.16 mm处。图 6(c)为t=1.0 s时基值电流(Ib)为50 A时的温度场。电弧最高温度为13 572 K,最高温位于钨针下方1.2 mm处。与t=0 s时相比,t=1.0 s时电弧最高温大于t=0 s时的电弧最高温。由于峰值电流时电弧温度的影响,造成后续基值电流时电弧温度略大于t=0 s时的电弧温度。此外,与峰值电流期间的电弧体积相比,基值电流期间电弧体积明显减小,仅能起维持电弧燃烧作用。
|
图 5 焊接电流 Fig.5 Welding current |
|
图 6 不同时刻电弧温度场云图 Fig.6 Cloud map of arc temperature field at different times |
图 6(b)为t=0.5 s时峰值电流(Ip)为120 A时电弧的温度场,可以看到,电弧等离子体的中心区域电弧温度梯度较小,电弧外部温度迅速降低。峰值时刻电弧最高温度为19 243 K,电弧最高温位于钨针下方1.4 mm处。由于角焊缝的形状,焊缝两侧的工件对电弧起到了一定的聚拢和压缩的作用。
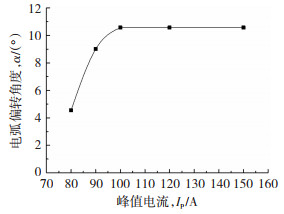
2.2 电弧磁偏吹从图 6模拟计算结果可以看出,电弧左右两侧温度场分布呈现非对称性,电弧向右侧Q235低碳钢一侧发生了一定角度的偏转。如图 6所示,电弧最高温并未在钨针所在轴线上。电弧中心的偏移导致电弧热输入在异种金属两侧不再等量分配,焊后会产生热应力集中、裂纹等焊接缺陷。通过改变模型峰值电流大小,取Ip=80、100、120、150 A,计算电弧温度场。图 7为不同峰值电流时电弧向Q235侧的偏转角度,可以看到,在低电流时电弧向Q235低碳钢侧偏转角度较小,为4°,当电流升高至100 A以上时,电弧偏转角度保持恒定,向304L不锈钢侧偏转11°。
|
图 7 不用电流时电弧偏转角度 Fig.7 Arc deflection angle without current |
针对前述模拟计算结果进行了试验验证,发现焊件尺寸及其材料与仿真条件一致。图 8(b)为使用CMOS高速工业相机拍摄的峰值电流为120 A时的电弧形态。对图片中的电弧偏转角度进行测量发现,电弧向Q235侧偏转约13°,与模型模拟结果基本相同。图 8(c)为使用TI400S红外热像仪拍摄的的电弧温度场,该设备的测温范围为233~1 973 K,超过测温范围将会显示为白色。通过与图 8(a)模型温度场对比,电弧外围温度场基本相同,均约为2 000 K,电弧温度场向Q235侧偏转了12°,与模型模拟结果相同,验证了模型的正确性。

|
图 8 峰值电流时电弧形态及温度场 Fig.8 Arc form and temperature field at peak current: (a) arc temperature field of model; (b) arc shape; (c) arc temperature field captured by infrared thermal imager |
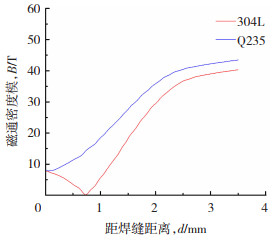
针对异种钢焊接时电弧的偏转现象开展了机理分析,探究了异种钢焊接电弧的磁场分布情况。图 9为Ip=120 A时电弧在阳极表面电弧磁通密度分布。图 9结果表明:电弧两侧在距离焊缝相同位置,304L侧电弧磁通密度大于Q235侧;工件表面电弧最小磁通密度位于Q235侧距离焊缝中心0.7 mm处。由于焊缝两侧材料的差异,右侧为Q235低碳钢,其相对磁导率常温下为285[18];而左侧为304L奥氏体不锈钢,相对磁导率为1。由于Q235材料良好的导磁性能,造成Q235侧电弧磁通密度降低,从而使Q235侧电弧磁场强度小于304L侧。电弧受到的Q235侧的电磁力小于304L侧,因此,电弧向Q235侧发生了一定角度的偏转。由于焊缝两侧材料导磁性能的巨大差异,导致焊接电弧向导磁性能好的一侧发生偏转,产生磁偏吹现象,最终导致电弧整体结构发生偏转。
|
图 9 焊件表面电弧磁通密度 Fig.9 Arc flux density on weldment surface |
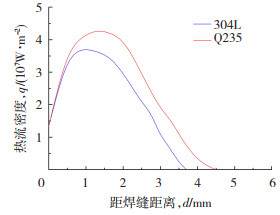
由于异种钢热导率、熔点等性能的差异,焊缝两侧材料对电弧热量的需求是不同的。图 10为Ip=120 A时异种钢焊件两侧热流密度分布情况,由于电弧的偏转,Q235侧热流密度明显大于304L侧,分布范围也更广。在阳极表面对热流密度进行积分获得阳热流极总量[19],即
| $ Q=\int_{\Omega} q \mathrm{~d} s $ | (10) |
利用式(10),对热流密度积分计算可得Q235一侧热流总量为359.9 W,304L一侧热流总量为247.3 W。Q235侧热流总量占总热流的59%。从图 10中可以看出,异种钢焊接时焊缝两侧电弧能量由于磁偏吹发生了调整,而异种钢焊缝两侧304L不锈钢的热导率约为Q235低碳钢的2倍,因此,需要对电弧热输入能量进行有效的合理分配。
|
图 10 阳极热流密度 Fig.10 Anodic thermal flow density |
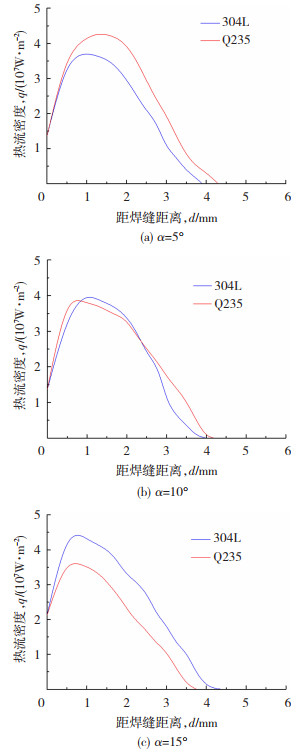
通过调整焊枪角度,对电弧能量在焊缝两侧的分配规律进行研究。将焊枪向右侧Q235钢偏转不同的角度使电弧逐渐向左侧304L侧偏转,图 11为焊枪不同偏转角度下阳极热流密度分布。从图 11可知,电弧热流主要分布在距离焊缝中心4.5 mm的范围内,且最大热流密度并未在焊缝处,而在距离焊缝1~2 mm处。随着焊枪角度向Q235侧的偏转,Q235侧电弧热流密度逐渐降低,电弧能量分布范围逐渐减小;304L侧电弧热流密度逐渐升高,电弧能量分布范围逐渐增大。在焊枪偏转10°时,电弧的磁偏吹现象被纠正,电弧偏转角度为0°,焊缝两侧热流密度分布基本相同。
|
图 11 焊枪向右偏转不同角度阳极热流密度 Fig.11 Anodic thermal flow density under different deflection angles of welding gun to the right |
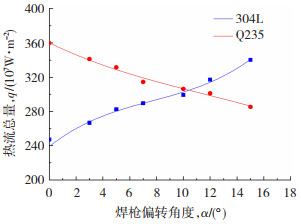
利用式(10)计算得到不同焊枪偏转角度下的阳极热流总量,热流密度随着焊枪角度的变化规律如图 12所示。对计算结果进行数值拟合,获得焊缝左右两侧热流总量与焊枪偏转角度的关系,即
| $ \left\{\begin{aligned} Q_{304 \mathrm{~L}}=& 0.460\ 6 \alpha^{3}-1.067\ 22 \alpha^{2}+\\ & 12.428\ 59 \alpha+239.031\ 93 \\ Q_{\text {Q235 }}=&-0.009\ 07 \alpha^{3}+0.315\ 21 \alpha^{2}-\\ & 7.615\ 3 \alpha+360.174\ 04 \end{aligned}\right.(0 \leqslant \alpha \leqslant 18) $ | (11) |
|
图 12 不同偏转角度下阳极热流总量 Fig.12 Total anode heat current at different deflection angles |
式中:Q304L、QQ235分别为304L侧和Q235侧的电弧总热量;α为焊枪偏转角度。
在不同焊枪偏转角度时,阳极左右两侧总热流量为610 W,随着焊枪角度的偏转,总热流量略有降低。焊接热效率为69.2%~71.6%,与文献[20]的计算结果相符。在焊枪偏转角度小于10°时,Q235侧总热输入大于304L侧;焊枪偏转角度为10°时,焊缝两侧总热输入基本相等;焊枪偏转角度大于10°时,Q235侧总热输入小于304L侧。
2.4 实验验证对上述不同焊枪偏转角度下电弧热输入对304L不锈钢和Q235低碳钢角焊缝焊接结果的影响进行焊接试验验证。采用与模型相同的焊接参数和工件材料, 焊接速度为100 mm/min。对焊接后的工件自然冷却,然后制作金相试件,观察熔池融合线。图 13分别为焊枪角度为0°、5°和10°时熔池熔合线。

|
图 13 不同焊枪偏转角度时焊缝熔合线 Fig.13 Fusion lines of welds at different deflection angles of welding gun |
由图 13实验结果可知:当焊枪偏转角度为0°时,由于电弧的磁偏吹现象以及材料热物理性能的差异,Q235侧获得电弧热量占总热量的59%,熔池主要位于Q235侧,Q235侧焊脚长度和熔深远大于304L侧;当焊枪向Q235侧偏转5°时,电弧向304L侧偏转,Q235侧获得的电弧热量减少,占总热量的54%,Q235侧熔池焊脚长度和熔深相比,焊枪偏转角度为0°时明显变小,熔池开始向304L侧转移;当焊枪向Q235侧偏转10°时,Q235侧获得的电弧热量占总热量的49%,304L侧获得较多的电弧热量,304L侧焊脚长度和熔深略大于Q235侧,获得了较好的焊接质量。实验结果表明,随着焊枪的偏转,304L不锈钢侧获得的电弧热量逐渐增多,Q235侧焊脚长度和熔深逐渐变小,熔池逐渐从Q235侧向304L侧转移,焊接质量逐渐提高。
3 结论1) 建立了异种钢角焊缝直流脉冲GTAW瞬态电弧模型。获得了脉冲电流作用下的峰值电流和基值电流时的电弧温度场,角焊缝对电弧起到了一定的聚拢和抬升的作用。
2) 采用实验与数值模拟相结合的方法,获得了不同焊接电流作用下的电弧形态。对不锈钢和低碳钢进行焊接时,电弧为非对称状态,电弧将会向低碳钢一侧发生偏转,且发生偏转的角度随着焊接峰值电流升高到100 A后保持不变。
3) 通过将焊枪角度向Q235侧偏转不同的角度,获得不同偏转角度下焊缝两侧电弧热流密度在焊缝两侧的分布规律,以及焊缝两侧的总热量与焊枪偏转角度的关系。随着偏转角度的不断增大,Q235侧热流密度和热流总量不断降低,304L侧不断升高,在偏转角度为10°时,两侧热流密度和热流总量基本保持一致。
4) 对不同焊枪偏转角度下电弧热输入对304L不锈钢和Q235低碳钢角焊缝焊接结果的影响进行焊接试验验证,研究发现,随着焊枪角度向Q235侧偏转,焊接质量逐渐提高,在焊枪偏转角度为10°时获得了较好的焊接质量。
| [1] |
WU W Y, HU S S, SHEN J Q. Microstructure, mechanical properties and corrosion behavior of laser welded dissimilar joints between ferritic stainless steel and carbon steel[J]. Materials and Design, 2015, 65: 855-861. DOI:10.1016/j.matdes.2014.09.064 |
| [2] |
BEHNAM S, HASSAN S, MAHDI R, et al. Microstructural, mechanical and corrosion properties of dissimilar joint between AISI A321 stainless steel and ASTM A537CL1 structural steel produced by GTAW process[J]. Metallurgical Research & Technology, 2019, 116(4): 418-429. DOI:10.1051/metal/2019012 |
| [3] |
李依依, 陆善平. 我国压水堆用材料与异材焊接[J]. 材料科学与工艺, 2020, 28(3): 1-8. LI Yiyi, LU Shanping. Materials for pressurized water reactors and dissimilar materials welding in China[J]. Materials Science and Technology, 2020, 28(3): 1-8. DOI:10.11951/j.issn.1005-0299.20200063 |
| [4] |
黄逸飞, 罗震, 敖三三, 等. 基于非对称热源的异种钢深熔TIG焊接数值模拟[J]. 机械工程学报, 2018, 54(2): 41-47. HUANG Yifei, LUO Zhen, AO Sansan, et al. Numerical simulation of keyhole TIG welding of dissimilar steels based on asymmetric heat source[J]. Journal of Mechanical Engineering, 2018, 54(2): 41-47. DOI:10.3901/JME.2018.02.041 |
| [5] |
黄本生, 陈权, 杨江, 等. Q345/316L异种钢焊接残余应力与变形数值模拟[J]. 焊接学报, 2019, 40(2): 138-144, 167. HUANG Bensheng, CHEN Quan, YANG Jiang, et al. Numerical simulation of welding residual stress and Distortion in Q345/316L dissimilar steel[J]. Transactions of the China Welding Institution, 2019, 40(2): 138-144, 167. DOI:10.12073/j.hjxb.2019400057 |
| [6] |
张伯奇, 蔡志鹏, 李克俭, 等. 异种钢焊接接头蠕变过程的有限元模拟[J]. 中国机械工程, 2015, 26(2): 266-271, 277. ZHANG Boqi, CAI Zhipeng, LI Kejian, et al. Finite element analysis of creep behavior of dissimilar steel welded joint[J]. China Mechanical Engineering, 2015, 26(2): 266-271, 277. DOI:10.3969/j.jssn.1004-132X.2015.02.025 |
| [7] |
王海燕, 牛春菊, 崔国涛, 等. 焊接工艺对TP304/SS400异种钢焊接接头组织和性能的影响[J]. 焊接学报, 2019, 40(5): 131-136, 167. WANG Haiyan, NIU Chunju, CUI Guotao, et al. Study of microstructure and properties of TP304/SS400 dissimilar welding joints under three processes[J]. Transactions of the China Welding Institution, 2019, 40(5): 131-136, 167. DOI:10.12073/j.hjxb.2019400140 |
| [8] |
DENG D, MURAKAWA H, LIANG W. Numerical and experimental investigations on welding residual stress in multi-pass butt welded austenitic stainless steel pipe[J]. Computational Materials Science, 2008, 42: 234-244. DOI:10.1016/j.commatsci.2007.07.009 |
| [9] |
RAKESH C, ASHA I, KANAK K. Stress analysis of dissimilar metal weld between carbon steel and stainless steel formed by transition grading technique[J]. Materials Today: Proceedings, 2015, 2(4/5): 1657-1644. DOI:10.1016/j.matpr.2015.07.093 |
| [10] |
李琴, 王于豪, 丁雅萍, 等. 焊接工艺参数对Q345钢平板焊接残余应力的影响[J]. 材料科学与工艺, 2020, 28(6): 80-87. LI Qin, WANG Yuhao, DING Yaping, et al. Effect of welding parameters on residual stress of Q345 steel plate welding[J]. Materials Science and Technology, 2020, 28(6): 80-87. DOI:10.11951/j.issn.1005-0299.20190037 |
| [11] |
蔡建鹏, 叶延洪, 张彦杰, 邓德安. 坡口形式对Q345/SUS304异种钢对接接头残余应力和变形的影响[J]. 机械工程学报, 2015, 51(10): 55-61. CAI Jianpeng, YE Yanhong, ZHANG Yanjie, et al. Study on influences of groove type on welding residual stress and deformation in Q345/SUS304 dissimilar steel butt-welded joints[J]. Journal of Mechanical Engineering, 2015, 51(10): 55-61. DOI: 10.3901/JME.2015.10.055 |
| [12] |
DURANTON P, DEVAUX J, ROBIN V, et al. 3D modelling of multipass welding of a 316L stainless steel pipe[J]. Journal of Materials Processing Technology, 2004(153-154): 457-463. DOI:10.1016/j.jmatprotec.2004.04.128 |
| [13] |
吴健文, 徐孟嘉, 范文艳, 等. 钛合金快频脉冲柔性波形调制TIG焊接工艺[J]. 机械工程学报, 2020, 56(6): 102-109. WU Jianwen, XU Mengjia, FAN Wenyan, et al. Flexible waveform interpulse TIG welding for titanium alloy[J]. Journal of Mechanical Engineering, 2020, 56(6): 102-109. DOI:10.3901/JME.2020.06.102 |
| [14] |
程世佳, 朱志明, 符平坡. 基于电弧图像的脉冲TIG焊电弧形态及特征温度演变规律[J]. 清华大学学报(自然科学版), 2021, 61(9): 994-1001. CHENG Shijia, ZHU Zhiming, FU Pingpo. Arc shape variations and characteristic temperatures of pulsed TIG welding arcs based on observed arc images[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(9): 994-1001. DOI:10.16511/j.cnki.qhdxxb.2020.25.035 |
| [15] |
肖磊, 樊丁, 黄健康. 交变磁场作用下的GTAW非稳态电弧数值模拟[J]. 机械工程学报, 2018, 54(16): 79-85. XIAO Lei, FAN Ding, HUANG Jiankang. Numerical simulation of unsteady arc in GTAW with alternate axial magnetic field[J]. Journal of Mechanical Engineering, 2018, 54(16): 79-85. DOI:10.3901/JME.2018.16.079 |
| [16] |
FAN H G, NA S J, SHI Y W. Numerical simulation of current density in gas tungsten arc welding including the influence of the cathode[J]. Journal of Engineering Manufacture, 2015, 211(4): 321-327. DOI:10.1243/0954405971516293 |
| [17] |
XIAO L, FAN D, HUANG J K. Tungsten cathode-arc plasma-weld pool interaction in the magnetically rotated or deflected gas tungsten arc welding configuration[J]. Journal of Manufacturing Processes, 2018, 32. DOI:10.1016/j.jmapro.2018.01.026 |
| [18] |
刘怡, 胡博, 代占鑫, 等. Q235钢短裂纹扩展的力-磁耦合模拟[J]. 金属热处理, 2018, 43(12): 226-231. LIU Yi, HU Bo, DAI Zhanxin, et al. Simulation of short crack propagation in Q235 steel based on coupling of stress and magnetic[J]. Heat Treatment of Metals, 2018, 43(12): 226-231. DOI:10.13251/j.issn.0254-6051.2018.12.045 |
| [19] |
刘政军, 李宇航, 苏允海. Ar与H2混合气体保护下GTAW电弧特性数值模拟[J]. 焊接学报, 2019, 40(7): 67-71, 164. LIU Zhengjun, LI Yuhang, SU Yunhai. Numerical simulation of arc characteristics under mixtures of argon and hydrogen in gas tungsten arc welding[J]. Transactions of the China Welding Institution, 2019, 40(7): 67-71, 164. DOI:10.12073/j.hjxb.2019400183 |
| [20] |
武传松. 焊接热过程与熔池形态[M]. 北京: 机械工业出版社, 2008: 16-19. WU Chuansong. Welding thermal processes and weld pool behaviors[M]. Beijing: China Machine Press, 2008: 16-19. |
 2021, Vol. 29
2021, Vol. 29


