电弧熔丝增材制造(Wire and Arc Additive Manufacturin,WAAM)是一种由三维坐标数据驱动,通过熔化同步供给的丝材,在基板上逐层堆积形成金属零件的一种直接制造技术[1-2]。与传统制造方法相比,WAAM具有装置简单,成形尺寸大,材料利用率高,制造成本低等优势[3-4]。
对电弧熔丝增材制造技术来说,最重要的是复杂构件的成形能力和成形质量[5]。科研人员从上述两个方面对WAAM成形技术进行了大量研究,主要集中在:1)成套设备与过程控制研究,工业机器人和数控系统具有较高的加工柔性和可操作性,而且还能保持较高的成形精度,因而被广泛应用于增材制造技术。Zhang等人[6]开发了由工业机器人、弧焊系统和路径规划软件组成的快速制造系统。路径规划软件可实现三维模型分层、路径规划、加工轨迹输出以及过程控制。焊枪和基板之间的距离对构件成形精度和表面质量具有较大的影响,距离过大,焊接过程易产生飞溅。Xiong等人[7]开发了一套视觉传感系统,用于实时监测并调整焊枪与基板之间的工作距离,使其始终维持在最佳距离,从而减少飞溅;2)堆焊工艺参数及方法优化,杨永强等人[8]采用单因素法研究工艺参数对单层单道焊缝尺寸的影响,确定了单层单道成形质量较好的工艺窗口。通过设计二次通用旋转组合试验,建立了基于二次回归方程的直臂体尺寸预测模型。方学伟[9]将焊缝截面与抛物线、余弦函数和圆弧曲线进行拟合,发现焊缝截面和抛物线具有最高的拟合度,提出了相邻焊缝斜顶搭接模型。Ding[10]探究了相邻焊缝搭接情况,提出理想搭接模型(相邻焊缝最佳中心距d=0.738w,w为熔宽),该搭接率下焊缝上表面具有最高的平整度;3)路径规划算法开发,Ding[11]通过提取每一个薄壁构件二维轮廓的中轴线,以中轴线为起始轮廓,由内而外生成轮廓偏置路径的MAT(Medial Axis Transformation)路径规划方法。MAT路径规划方法消除了传统路径规划方法几何中心形成的孔隙。Florent[12]对往复直线路径和轮廓偏置路径进行了对比研究,提出适用于薄壁构件的MPP(Modular Path Planning)路径规划方法。该方法将复杂几何轮廓分解为多个简单区域,每一个区域均采用往复直线路径规划方法,但是会根据不同区域的几何特征匹配最佳的工艺参数。
以上研究多集中在金属增材制造设备的研发、成形工艺参数优化及薄壁构件路径规划算法的开发,但是对于具有复杂几何特征的大尺寸金属构件的成形路径规划方法研究较少。
WAAM中路径规划方法的选择应考虑以下3个主要影响因素:1)起熄弧次数,成形过程中起熄弧处形成的弧坑不仅影响单层表面质量,还能造成弧坑塌陷;2)几何还原度,成形过程中二维轮廓的几何还原度高,构件后期所需要的精加工量就少;3)成形能力,应当选择填充能力强、灵活性好的路径规划方法,使其可以填充大多数复杂二维轮廓。
WAAM中常用填充路径有:1)单向直线路径,该方法无法形成一条连续的沉积路径,需要反复起熄弧,易形成弧坑塌陷;2)往复直线路径,该方法具有较高的成形能力,可以实现复杂轮廓的完全填充且需要的起熄弧次数较少,但是存在较多拐点路径,拐点路径主要位于切片轮廓处,而焊枪在拐点路径处速度变化较大,可能造成大量的欠堆积或过堆积;3)轮廓偏置路径,该方法是以切片轮廓为基础,由外向内等距偏置而得到整体填充路径。该方法具有较高的几何还原度,但是由外而内偏置时,当内部区域无法完成下一次等距偏置时,易在中心部位形成孔隙,当轮廓偏置次数过多时,必须要考虑多边形的相交情形,增加了算法的复杂度;4)螺旋线路径,该方法可以形成一条连续、平滑、没有尖角的填充路径,但是不适用于填充形状过于复杂的二维轮廓,尤其是带有孔洞的二维轮廓;5)分区路径,分区填充路径可以有效减少拉丝现象和因应力集中所导致的翘曲变形,但是将复杂轮廓截面划分为多个子区域,在不同子区域间过渡时会增加大量的空行程,还会增加起熄弧数量;6)分形线路径可以打印出表面光滑、材料分布均匀的分层面,但是该路径中90°拐点过多,会造成大量的过堆积,严重影响表面平整度[13-14]。
当前电弧熔丝增材制造技术一般只选用某一种填充路径和成形工艺参数,但对于具有复杂几何特征的大尺寸金属构件,采用单一的填充路径往往不能很好地完成截面的高效率完全填充,工件也无法取得较好的成形质量[13-14]。综合考虑上述方法的优缺点,针对具有复杂几何特征的大尺寸金属构件提出轮廓偏置路径和往复直线路径相结合的复合路径规划方法,复合路径规划算法的实现流程如图 1所示。该算法的特点:1)切片轮廓只进行一次偏置,降低算法的复杂度,提高工作效率;2)优化了切片轮廓向内偏置距离d,消除了两种路径搭接时出现的缺陷,提高了表面质量;3)外轮廓路径用于提高几何还原度,往复直线路径用于填充内部区域,在提高几何还原度的同时避免几何中心出现孔隙。

|
图 1 复合路径规划算法流程图 Fig.1 Flow chart of compound path planning algorithm |
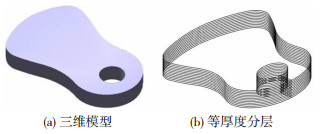
金属增材制造技术的原材料可按物理状态分为粉末和丝材两种。以金属粉末为原料的增材制造技术成形精度高,因此需要非常高的分层精度,其主要分层算法有自适应分层算法、基于哈希表的分层算法、基于三角面片法向量的分层算法。而以金属丝材为原料的增材制造技术的主要优点是成形尺寸大,成形效率高,单道焊缝的熔宽尺寸为3~6 mm之间,余高尺寸为1~2 mm之间;多层多道构件的成形误差相对较大,因此不需要非常高的分层精度,用计算复杂度较低的等厚度分层算法就可以达到使用要求。如图 2(a)所示为平衡结构的三维模型,图 2(b)为等厚度分层结果示意图。
|
图 2 等厚度分层结果示意图 Fig.2 Results of equal thickness slicing: (a)three-dimensional model; (b)equal thickness slicing |
通过等厚度分层算法可以得到三维模型的切片轮廓,提取任意层切片轮廓实现复合路径填充。复合路径规划方法中最核心的问题就是:1)切片轮廓偏置时偏置点的计算方法;2)偏置得到的内部填充区域如何实现往复直线填充。
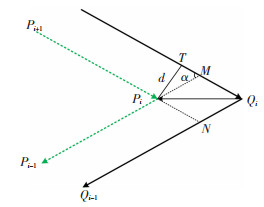
1.2.1 轮廓偏置路径中偏置点计算方法在增材制造中,切片轮廓是STL格式的三维模型和切平面求交点得到的。STL格式是通过三角面片构造出整个三维模型,因而切片轮廓是由多线段构成的封闭轮廓,偏置点的计算方法如图 3所示。截取切片轮廓的一部分,切片轮廓顶点Qi偏置一定距离d后得到新顶点Pi。顶点Qi的坐标已知,只需求出矢量Qi Pi的值,便可以得到新顶点Pi的坐标值。设原顶点Qi+1、Qi、Qi-1的坐标分别为(xi+1, yi+1)、(xi, yi)、(xi-1, yi-1),e1,e2分别为有向线段Qi+1Qi,QiQi-1的单位矢量,i、j分别为X轴和Y轴的单位向量。延长Pi+1Pi和PiPi-1分别与直线QiQi-1,Qi+1Qi交于N和M,得到平行四边形PiMQiN,α=∠PiMT[15]:
|
图 3 偏置点计算方法示意图 Fig.3 Schematic diagram of offset point calculation method |
| $ \boldsymbol{e}_{1}=x_{1} \boldsymbol{i}+y_{1} \boldsymbol{j} $ | (1) |
| $ \boldsymbol{e}_{2}=x_{2} \boldsymbol{i}+y_{2} \boldsymbol{j} $ | (2) |
| $ \left|\overrightarrow{Q_{i} N}\right|=\left|\overrightarrow{N P_{i}}\right|=\frac{d}{\sin \alpha} $ | (3) |
| $ \sin \alpha=\left|\boldsymbol{e}_{1}+\boldsymbol{e}_{2}\right| /\left(\left|\boldsymbol{e}_{1}\right| \cdot\left|\boldsymbol{e}_{2}\right|\right) $ | (4) |
| $ \begin{gathered} \overrightarrow{Q_{i} P_{i}}=\overrightarrow{Q_{i} N}+\overrightarrow{N P_{i}}= \\ \left(\frac{\overrightarrow{Q_{i} Q_{i-1}}}{\overrightarrow{Q_{i} Q_{i-1}}}-\frac{Q_{i} Q_{i+1}}{\overrightarrow{Q_{i} Q_{i+1}}}\right)\left|\overrightarrow{N P_{i}}\right|=\frac{\left(e_{2}-e_{1}\right)}{\left|e_{1} \times e_{2}\right|} \end{gathered} $ | (5) |
| $ x_{1}=\frac{x_{i}-x_{i-1}}{\sqrt{\left(x_{i}-x_{i-1}\right)^{2}+\left(y_{i}-y_{i-1}\right)^{2}}} $ | (6) |
| $ y_{1}=\frac{y_{i}-y_{i-1}}{\sqrt{\left(x_{i}-x_{i-1}\right)^{2}+\left(y_{i}-y_{i-1}\right)^{2}}} $ | (7) |
| $ x_{2}=\frac{x_{i+1}-x_{i}}{\sqrt{\left(x_{i+1}-x_{i}\right)^{2}+\left(y_{i+1}-y_{i}\right)^{2}}} $ | (8) |
| $ y_{2}=\frac{y_{i+1}-y_{i}}{\sqrt{\left(x_{i+1}-x_{i}\right)^{2}+\left(y_{i+1}-y_{i}\right)^{2}}} $ | (9) |
通过上式,可以求得Pi点的坐标值.
| $ \begin{aligned} &x_{i}^{\prime}=x_{i}+ \\ &\frac{d\left(x_{i+1}-2 x_{1}+x_{i-1}\right)}{\left|y_{i+1}\left(x_{i}-x_{i-1}\right)-y_{i}\left(x_{i+1}-x_{i-1}\right)+y_{i-1}\left(x_{i+1}-x_{i}\right)\right|} \\ &y_{i}^{\prime}=y_{i}+ \\ &\frac{d\left(y_{i+1}-2 y_{1}+y_{i-1}\right)}{\left|y_{i+1}\left(x_{i}-x_{i-1}\right)-y_{i}\left(x_{i+1}-x_{i-1}\right)+y_{i-1}\left(x_{i+1}-x_{i}\right)\right|} \end{aligned} $ |
按照上述方法可以求得各点偏置后的坐标,按照顺序依次连接便可以得到偏置后的几何轮廓,即为内部填充区域。
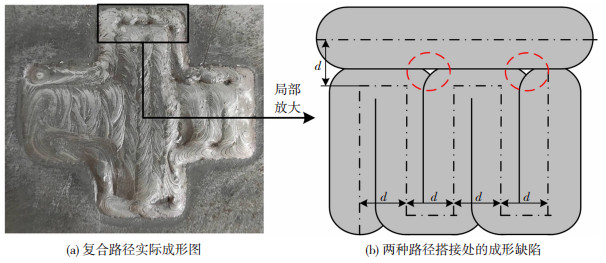
1.2.2 轮廓偏置距离优化相邻焊缝搭接距对于单层多道焊缝表面成形质量至关重要,不同的焊接工艺应当采用不同的搭接距。经过大量试验,发现适用于等离子弧增材制造的理想搭接距离为相邻焊缝中心距离d=0.738 w[10],w为熔宽。但是在试验中发现,轮廓偏置路径和往复直线路径的搭接区域会出现孔隙,影响成形质量。为了消除该搭接区域出现的孔隙,应当在不同类型的路径相互搭接时采用不同的搭接距。图 4(a)所示为复合路径的实际成形图,可以看到两种路径的搭接处存在孔隙(如图 4(b)所示),其余地方均不存在表面缺陷。究其原因,往复直线路径之间采用理想搭接可以得到很好的表面质量,但是为了将其连接成一条连续的路径,导致成形路径中边缘处存在过多的拐点,而焊缝在拐点处的成形为圆弧形,当相邻的两个拐点路径和外轮廓路径相互搭接时,就在该搭接处形成欠堆积区域,从而出现孔隙。
|
图 4 轮廓偏置路径和往复直线路径搭接处存在的问题 Fig.4 The problem existing at the overlap of contour offset path and reciprocating straight path: (a)actual forming diagram of compound path; (b)forming defects at the overlap of two paths |
相邻焊缝相互搭接时其中心距为d=0.738 w,则两个焊缝的搭接长度为0.262 w。结合上述分析,相邻的两个拐点路径和外轮廓路径相互搭接时的实际搭接长度只有0.146 w(推导过程较为简单,不再赘述)。为了消除孔隙,应将往复直线路径拐点处和外轮廓路径的搭接长度修正到0.262 w。根据公式(10)可以求得优化后的外轮廓偏置距离d′:
| $ d^{\prime}=d-d_{1}-d_{2} $ | (10) |
式中:d为相邻焊缝理想中心距(d=0.738 w);d1为理想搭接时两个焊缝搭接部分的长度(d1=0.262 w);d2为拐点路径实际搭接长度(d2=0.146 w)。
经计算优化后的偏置距离d′=0.591 w,因此在复合路径规划方法中外轮廓偏置距离均为过搭接(d=0.591 w),往复直线路径之间的偏置距离均为理想搭接(d=0.738 w)。
1.2.3 往复直线路径生成方法上文介绍了轮廓偏置的计算方法,并对偏置距离进行了优化,提取偏置轮廓使用往复直线路径对其进行填充。往复直线路径是通过求一系列扫描线与轮廓的交点坐标,再将交点坐标以特定的方式读取得到的,其具体的生成过程如下:
1) 本算法中采用水平方向的扫描线进行填充,根据偏置轮廓的x坐标确定扫描线的生成范围[xmin, xmax],再根据公式(11)确定扫描线的个数N;
| $ N= { floor }\left(\left(x_{\max }-x_{\min }\right) / d\right) $ | (11) |
2) 根据设定的扫描线偏置间距d,生成所有扫描线的x坐标矩阵[xmin+d…xmin+id…xmin+nd];
3) 根据公式(12)确定扫描线和偏置轮廓交点的Y坐标,交点的X坐标就是扫描线的x值;
| $ Y=\frac{y_{m}-y_{n}}{x_{m}-x_{n}}\left(X-x_{n}\right)+y_{n} $ | (12) |
4) 将交点坐标数据以Z字形输出。
以当前扫描线的终点为参考点,可根据公式(13)分别计算参考点与下一条直线两个端点之间的距离,与参考点距离较近的端点作为下一个连接点,以此类推,直至得到完整的往复直线路径。
| $ d=\sqrt{\left(x_{m}-x_{n}\right)^{2}+\left(y_{m}-y_{n}\right)^{2}} $ | (13) |
通过上述步骤可以得到完整的加工路径数据,包括内部的往复直线路径和用于提高几何精度的外轮廓路径。图 5展示了平衡结构其中一层的整体路径生成过程,需要注意的是,在输出路径时要先输出往复直线路径,再将外轮廓路径输出,这样可以达到更好的成形效果。

|
图 5 复合路径规划方法生成过程 Fig.5 Generation process of compound path planning method: (a)forming inner contour by outer contour offset; (b)extracting inner contour; (c)generating scan line; (d)finding the intersection of the inner contour and the scan line; (e)generating zigzag path; (f) generating full tool path |
三维模型经过分层处理和路径规划后只能得到坐标点数据,必须将这些数据转换成数控机床可以识别的加工路径,并由数控指令通过数控系统对弧焊系统进行实时控制,实现增材制造的离线编程。
在数控机床中,采用G开头的数控代码对加工轨迹进行控制。数控机床和弧焊系统属于组合设备,因此没有统一的数控代码对弧焊系统进行实时控制。本文采用自主开发的二次代码对弧焊系统进行控制,开发代码如表 1所示。
| 表 1 数控等离子弧增材制造系统二次开发代码 Table 1 Secondary development code for CNC plasma arc additive manufacturing system |
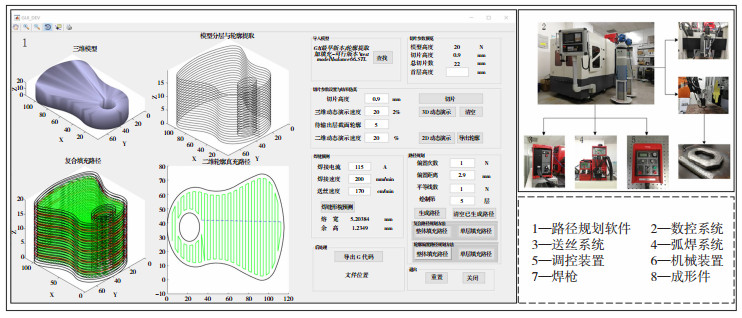
利用数控弧焊增材制造系统进行实验验证,实验系统如图 6所示。该系统主要由路径规划软件和数控弧焊系统组成。路径规划软件包括3D模型的导入与分层、焊缝形貌预测、复合路径规划、G代码输出。数控弧焊系统由五轴数控加工系统、工作平台、焊枪、弗尼斯焊接控制柜、焊接过程调控装置AVC、送丝控制柜及保护气组成。实验采用的熔覆材料为304不锈钢,其直径为0.8 mm。焊接保护气为纯氩气,保护气流量为15 L/min。等离子气为氩气,等离子气流量为1.3 L/min。基板材料为Q235,其尺寸为340 mm×200 mm×12 mm(长×宽×高)。为了提高成形质量减少液滴飞溅,焊枪喷嘴和基板之间的距离设定为3~5 mm。试验所用的成形工艺参数如表 2所示。
|
图 6 数控等离子弧增材制造系统 Fig.6 CNC plasma arc additive manufacturing system |
| 表 2 成形工艺参数 Table 2 Forming process parameters |
图 7展示了“十”字结构在不同路径规划方法下的成形结果,其中的红色区域为成形缺陷。从图中可以看出,往复直线路径外轮廓的几何还原度较低(图 7中①);轮廓偏置路径的几何还原度较高,但是在几何中心存在间隙(图 7中②);未采用优化的复合路径规划方法中(外轮廓和往复直线路径之间的距离为0.738 w),两种路径的搭接处存在较多的孔隙,影响成形质量(图 7中③);采用优化后的复合路径规划方法后(外轮廓和往复直线路径之间的距离为0.591 w,往复直线路径之间的距离为0.738 w),孔隙被完全消除,几何还原度较高,表面质量达到了预期目标(图 7中④)。

|
图 7 不同路径规划方法下的成形结果 Fig.7 Forming results under different path planning methods |
为了验证复合路径规划方法在实际应用中的可行性及适用性,利用本文开发的路径规划软件生成图 8所示二维轮廓的填充路径(图中绿线为外轮廓路径,黑线为往复直线路径,虚线为焊枪快速移动路径)。图示的二维轮廓较为复杂,人工难以输出精确的成形路径加工数据,而采用本文开发的路径规划软件可以快速输出加工轨迹。

|
图 8 复杂二维轮廓的成形试验 Fig.8 Forming test on complex two-dimensional profile: (a)filling path of two-dimensional profile of pore structure; (b)filling path of two-dimensional profile of plane structure; (c)actual forming results of structure (a); (d)actual forming results of structure (b) |
图 8(a)的成形尺寸为120 mm×80 mm,图 8(b)的成形尺寸为200 mm×200 mm,实际成形结果如图 8(c)和(d)所示。从成形结果可以看出,几何轮廓内部填充致密、均匀,不存在单一路径中存在的缺陷,增加外轮廓路径后,构件的几何轮廓还原度得到改善,实际成形件高度与设计相比误差为-0.1~0.1 mm, 实际成形件表面尺寸与设计相比误差为0.3~1.5 mm。外轮廓路径与往复直线路径搭接处也不存在孔隙,构件表面质量达到了预期目标。
3 结论1) 开发了复合路径规划算法,可以对复杂大尺寸切片几何轮廓进行路径规划。
2) 对外轮廓路径和往复直线路径的搭接距进行了优化,可有效避免不同类型路径搭接时出现的孔隙。
3) 复合路径规划方法提高了构件表面成形质量且成形误差较小,几何还原度得到改善。
| [1] |
DING J, COLEGROVE P, MEHNEN J, et al. Thermo-mechanical analysis of wire and arc additive layer manufacturing process on large multi-layerparts[J]. Computational Materials Science, 2011, 50(12): 3315-3322. DOI:10.1016/j.commatsci.2011.06.023 |
| [2] |
刘海华, 赵淘, 张志臣, 等. 横向稳态磁场作用下微束等离子电弧数值分析[J]. 材料科学与工艺, 2021, 29(1): 59-65. LIU Haihua, ZHAO Tao, ZHANG Zhichen, et al. Numerical analysis of micro-plasma arc under the action oftransverse steady state magnetic field[J]. Materials Science and Technology, 2021, 29(1): 59-65. DOI:10.11951/j.issn.1005-0299.20190316 |
| [3] |
卢振洋, 刘峰, 蒋凡, 等. 电弧热丝变极性等离子弧增材制造铝合金成型尺寸预测[J]. 稀有金属材料与工程, 2019, 48(2): 524-530. LU Zhenyang, LIU Feng, JIANG Fan, et al. Prediction of forming size of aluminum alloy by arc hot wire variable polarity plasma arc additive manufacturing[J]. Rare Metal Materials and Engineering, 2019, 48(2): 524-530. |
| [4] |
李明祥, 张涛, 于飞, 等. 金属电弧熔丝增材制造及其复合制造技术研究进展[J]. 航空制造技术, 2019, 62(17): 14-21. LI Mingxiang, ZHANG Tao, YU Fei, et al. Research progress of wire and arc additive manufacturing and hybrid manufacturing technology for metal components[J]. Aeronautical Manufacturing Technology, 2019, 62(17): 14-21. DOI:10.16080/j.issn1671-833x.2019.17.014 |
| [5] |
WU B T, PAN Z, DING D H, et al. A review of the wire arc additive manufacturing of metals: properties, defects and quality improvement[J]. Journal of Manufacturing Processes, 2018, 35(10): 127-139. DOI:10.1016/j.jmapro.2018.08.001 |
| [6] |
ZHANG Y M, LI P, CHEN Y. Automated system for welding-based rapid prototyping[J]. Mechatronics, 2002, 12(1): 37-53. DOI:10.1016/S0957-4158(00)00064-7 |
| [7] |
XIONG J, ZHANG G. Adaptive control of deposited height in GMAW-based layer additive manufacturing[J]. Journal of Materials Processing Technology, 2014, 214(4): 962-968. DOI:10.1016/j.jmatprotec.2013.11.014 |
| [8] |
杨永强, 翁昌威, 周权, 等. 316 L不锈钢等离子增材制造工艺与尺寸预测模型研究[J]. 机械工程学报, 2019, 55(15): 31-38. ZHANG Yongqiang, WENG Changwei, ZHOU Quan, et al. Research on 316 L stainless steel plasma additive manufacturing process and size prediction model[J]. Journal of Mechanical Engineering, 2019, 55(15): 31-38. DOI:10.3901/JME.2019.15.031 |
| [9] |
方学伟, 白浩, 姚云飞, 等. 冷金属过渡电弧增材制造多道搭接工艺研究[J]. 机械工程学报, 2020, 56(1): 141-147. FANG Xuewei, BAI Hao, YAO Yunfei, et al. Research on multi-lap technology of cold metal transition arc additive manufacturing[J]. Journal of Mechanical Engineering, 2020, 56(1): 141-147. DOI:10.3901/JME.2020.01.141 |
| [10] |
DING D, PAN Z, et al. A multi-bead overlapping model for robotic wire and arc additive manufacturing (WAAM)[J]. Robotics and Computer-Integrated Manufacturing, 2015, 31: 101-110. DOI:10.1016/j.rcim.2014.08.008 |
| [11] |
DING D, PAN Z, et al. A practical path planning methodology for wire and arc additive manufacturing of thin-walled structures[J]. Robotics and Computer-Integrated Manufacturing, 2015, 34: 8-19. DOI:10.1016/j.rcim.2015.01.003 |
| [12] |
FLORENTM, HELEN L, DING Jialuo, et al. A modular path planning solution for wire+Arc additive manufacturing[J]. Robotics and Computer Integrated Manufacturing, 2019, 60: 1-11. DOI:10.1016/j.rcim.2019.05.009 |
| [13] |
方力, 侯智文, 黄俊润, 等. 电弧熔丝增材制造复合填充路径规划算法[J]. 南京航空航天大学学报, 2019, 51(1): 98-104. FANG Li, HOU Zhiwen, HUANG Junrun, et al. Composite filling path planning algorithm for wire and ARC additive manufacturing[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2019, 51(1): 98-104. DOI:10.16356/j.1005-2615.2019.01.015 |
| [14] |
梁少兵, 王凯, 丁冬红, 等. 电弧增材制造路径工艺规划的研究现状与发展[J]. 精密成形工程, 2020, 12(4): 86-93. LIANG Shaobing, WANG Kai, DING Donghong, et al. Research status and development of wire arc additive manufacturing path planning[J]. Journal of Netshape Forming Engineering, 2020, 12(4): 86-93. DOI:10.3969/j.issn.1674-6457.2020.04.009 |
| [15] |
朱传敏, 许田贵, 朱啟太. 复合式路径填充算法的熔融沉积制造[J]. 现代制造工程, 2010, 2(8): 89-92. ZHU Chuanmin, XU Tiangui, ZHU Qitai. An algorism for FDM based on complex filling path[J]. Modern Manufacturing Engineering, 2010, 2(8): 89-92. DOI:10.16731/j.cnki.1671-3133.2010.08.012 |
 2022, Vol. 30
2022, Vol. 30


