Ti₂AlNb合金是一种具有良好应用前景的高温结构材料，其可以在600~750 ℃长时间服役^[1-3]，相较于传统钛合金，其具有高温强度高、抗氧化、抗蠕变性能好的优点^[4-5]。Ti₂AlNb合金为多相合金，由O相(Ti₂AlNb相)、α₂相和B2相3种有序相组成，微观组织复杂。经过不同的热变形和热处理过程，其会产生不同的微观组织形貌^[6-7]，而不同组织对材料的力学性能具有显著的影响^[8]，即使在同一组织形貌类型下，通过不同处理过程获得形貌微观参数不同，如双态组织中O相的片层宽度不同，其力学性能也具有明显差异^[9]。由于Ti₂AlNb合金成形温度高，成形获得的高温组织力学性能较差，因此，在成形后需要通过热处理对构件的力学性能进行调控。成形和热处理参数都会影响到热处理过程中的组织演变，进而影响材料的力学性能。因此，在Ti₂AlNb合金构件的塑性加工过程中，不仅要对成形构件的形状和尺寸进行控制，还需要对构件的微观组织和力学性能进行控制，但传统的试错法难度高，工作量大，成本高。通过全流程模拟的方法对构件的成形、微观组织和力学性能一体化预测是塑性加工领域一个重要的发展方向。

国内外学者对塑性加工过程中的组织和力学性能演变的模拟进行了大量的研究。Cai等^[10]通过相场法对镁合金热变形过程中的非连续再结晶过程进行了模拟，通过相场模拟，获得了晶粒再结晶过程的拓扑信息、平均晶粒尺寸以及微观组织演变带来的宏观应力应变关系的改变。Xu等^[11]通过元胞自动机模拟了Ti55热压缩过程中的动态再结晶。Zhang等^[12]通过元胞自动机对7055铝合金的热压缩过程动态再结晶进行了模拟。Sherstnev等^[13]建立了考虑再结晶的5083铝合金粘塑性本构方程，并嵌入到了有限元软件FORGE 2008中进行了5083铝合金热变形的模拟。武永等^[14]建立了Ti₂AlNb合金基于内变量的粘塑性本构方程，对杯形件成形过程中的微观组织演变进行了模拟。车俊铁等^[15]建立了不同挤压工艺条件下晶粒度的人工神经网络预测的方法，实现了AZ31镁合金热挤压条件下晶粒度的预测。目前，对于塑性加工过程中微观组织演变的模拟，大多数工作仍局限于成形过程本身，针对于包括成形和后续热处理的全流程的组织模拟的研究报道较少。而实验和生产中，Ti₂AlNb合金构件的服役组织和力学性能，不仅与其变形过程中的组织和力学性能的演变有关，也与其热处理过程中的组织和力学性能演变有关^[16]。因此，在构件组织和力学性能的模拟和预测中，需要考虑包括塑性变形和热处理在内的全过程的影响。

材料的塑性加工过程是一个高度非线性的过程，并且在成形过程中，各种影响成形件质量的因素交织在一起，增加了成形件的质量预测和工艺参数的制定和优化的难度，而机器学习为此提供了一个有效的方法。通过机器学习的方法不需要建立复杂的模型就可以实现成形过程中复杂非线性关系的构建。其在塑性加工领域具有广泛的应用前景，陈光耀等^[17]通过机器学习的方法实现了管材弯曲的回弹预测和补偿。张梓煜等^[18]通过机器学习的方式对锻件的拔长变形进行了预测。何纯玉等^[19]以神经网络对线材的力学性能进行了预测。崔鑫^[20]等提出了PSO-BP铝合金性能预测模型，实现了不同工艺条件下流动应力的预测。综上所述，目前塑性加工领域人工学习的应用，主要集中在特定工艺条件下宏观变形和性能的预测，忽略了塑性加工中变形件变形、组织和力学性能的不均匀性。通过将机器学习与有限元模拟的结合，不仅可以实现在不同成形- 热处理条件下微观组织和力学性能的预测，还可以实现成形件不同位置组织性能差异的分析。

Ti₂AlNb合金的最佳成形温度通常在950~1 000 ℃，其高温组织为塑性较差的等轴组织，因此，在成形后，需要通过时效处理的方式对Ti₂AlNb合金的微观组织和力学性能进行调控，其时效温度通常在750~900 ℃。

本文采用的实验材料为Ti₂AlNb合金轧制板材，合金的名义成分为Ti-22Al-24.5Nb-0.5Mo。板材的初始组织为双态组织，如图 1(a)所示。为了研究变形和热处理对Ti₂AlNb合金构件组织和服役性能的影响，本文对Ti₂AlNb合金轧制板材进行了固溶- 时效处理和预变形- 时效处理，实验参数如表 1所示。固溶处理的保温时间为25 min。预变形- 时效处理中采用高温拉伸的方式进行预变形，试样在变形前保温15 min。

图 Figure1(Fig.Figure1)

图 1 Ti2AlNb合金板材原始组织(a)和970 ℃，应变速率0.001 s-1，应变0.45条件下的变形组织(b) Fig.1 Microstructure of as-received Ti2AlNb alloy sheets(a) and deformed microstructure under conditions of 970 ℃, strain rate of 0.001 s-1, and strain of 0.45(b)

表1(Table 1)

表 1 本文实验参数 Table 1 Experimental parameters of this paper 变形温度/℃ 应变 应变速率/s-1 时效温度/℃ 时效时间/min 970 0 0 775 120 970 0 0 800 120 970 0 0 825 120 970 0 0 850 120 970 0 0 875 120 970 0 0 825 30 970 0 0 825 60 970 0 0 825 240 970 0 0 825 480 950 0 0 825 120 990 0 0 825 120 970 0.15 0.001 825 120 970 0.45 0.001 825 120 970 0.60 0.001 825 120 970 0.75 0.001 825 120 970 0.45 0.100 825 120 970 0.45 0.010 825 120 970 0.60 0.010 825 120 950 0.15 0.100 800 60 950 0.75 0.001 850 240 970 0.45 0.100 850 480 970 0.15 0.010 875 240 970 0.75 0.001 825 60 990 0.45 0.100 875 120 990 0.15 0.001 825 480

表 1 本文实验参数 Table 1 Experimental parameters of this paper

图 1(b)所示为Ti₂AlNb合金进行970 ℃ & 0.001 s^-1& 0.45后的变形组织。试样高温变形组织为服役温度下性能较差的等轴组织。图 2为970 ℃，应变速率0.001 s^-1条件下预变形试样825 ℃进行2 h时效处理后的微观组织。由图 2可以看到，变形后时效处理的组织为典型的双态组织，B2相基体上分布着等轴状的O/α₂相和时效过程中析出的片层O相，等轴状的O/α₂相由变形过程中残留的α₂相和其与B2相发生包析反应生成的O相壳层组成。本文采用Image Pro Plus软件对微观组织中片层厚度进行了测量和统计。相对于未变形- 热处理组织，变形- 热处理组织片层的厚度发生了粗化(固溶- 时效组织中O相片层厚度为0.067 μm)，且片层厚度随着预应变量的增加而增厚(如图 3所示)。

图 Figure2(Fig.Figure2)

图 2 预应变: (a) 0.15，(b) 0.45，(c) 0.6和(d) 0.75试样在825 ℃进行2 h时效处理后的微观组织 Fig.2 Microstructure of samples with prestrain of: (a) 0.15, (b) 0.45, (c) 0.6, and (d) 0.75 after aging treatment at 825 ℃ for 2 h

图 Figure3(Fig.Figure3)

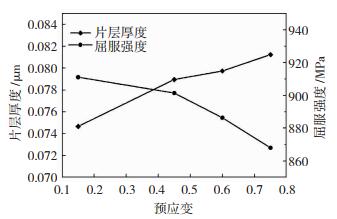
图 3 970 ℃应变速率0.001 s-1条件下不同预应变量试样经825 ℃/2 h时效处理后的O相厚度和650 ℃屈服强度变化 Fig.3 Variation of thickness of O phase and yield strength(650 ℃)of samples with different prestrain under conditions of 970 ℃ and strain rate of 0.001 s-1 after aging treatment at 825 ℃ for 2 h

具有不同预应变的浅样，经825 ℃/2 h时效处理后，其650 ℃的屈服强度存在差异，如图 3所示，可以看到，随着预应变量的增加，材料的屈服强度逐渐降低，而其屈服强度高于未变形的固溶- 时效试样(970 ℃固溶，825 ℃时效2 h试样强度为818 MPa)。变形- 时效后Ti₂AlNb合金的强度，不仅与材料中片层的厚度有关，还与材料在成形过程中残留的位错密度有关，而材料中残余的位错密度与成形的温度、应变、应变速率以及后续的时效条件有关。在时效处理中，相变和回复作用会部分消除变形产生的残余位错，时效后材料的力学性能取决于残余的位错含量和O相片层厚度等微观组织参量。变形产生的位错对时效试样力学性能的影响包括两方面。一方面，由于变形而产生大量的位错，在时效过程中，位错在回复和相变的作用下而降低，而这些位错在热处理过程中不能完全消除，由于位错强化的作用，经过预变形的试样相对于单纯进行固溶- 时效的试样，材料的屈服强度提高。另一方面，由于变形而导致材料的畸变能增加，畸变能的增加有利于相变的发生，对于O相片层析出这种扩散型相变，位错可以提供更多的形核位置，同时有利于材料中元素的扩散，加快相变的进程，因此，随着应变量的增加，材料微观组织中的片层厚度逐渐增加。当因片层厚度增加导致的强度降低占主导时，合金屈服强度随着应变量的增加而降低。

综上所述，Ti₂AlNb合金构件在成形过程中的变形量，对经过热处理调控后的构件微观组织和力学性能仍具有明显的影响，构件在成形过程中各处的应变量往往具有差异，而正是这种差异，导致了构件服役组织和力学性能在构件各处的差异，因此，在对构件服役组织和性能仿真和预测时，变形量对组织和性能的影响是不可忽略的。

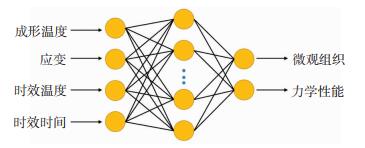
通过机器学习中的回归分析可以建立变量之间的关系，实现目标值的预测。神经网络是回归分析中常用的算法，其能够高效地对复杂的非线性关系进行建模。本文将通过神经网络算法建立变形- 热处理参数和构件组织- 力学性能之间的关系，以实现构件组织和力学性能的预测。本文采用了双层前馈神经网络算法，其包括输入层、隐藏层和输出层，各层之间信号单向传递，是应用最广泛的人工神经网络算法之一。本文通过Levenberg-Marquardt算法对神经网络进行训练，通过神经网络进行的微观组织和力学性能的预测模型示意图如图 4所示。

图 Figure4(Fig.Figure4)

图 4 微观组织和力学性能预测神经网络模型示意图 Fig.4 Schematic diagram of neural network model for predicting microstructure and mechanical properties

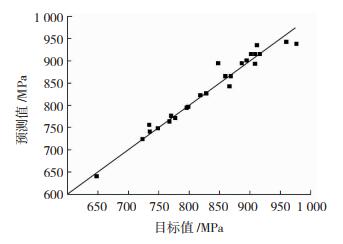
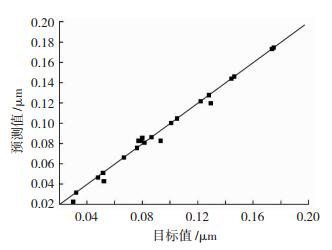
本文采用表 1中不同参数的固溶- 时效处理和预变形- 时效处理实验数据对建立的组织性能预测神经网络进行了训练，用前馈神经网络可以获得良好的训练效果。屈服强度和O相片层宽度的目标值(实验值)与预测值分布如图 5和图 6所示，目标值与预测值相关系数R达到0.97，两者一致性较好。

图 Figure5(Fig.Figure5)

图 5 650 ℃屈服强度目标值与预测值关系 Fig.5 Relationship between target value and predicted value of yield strength at 650 ℃

图 Figure6(Fig.Figure6)

图 6 O相片层厚度目标值与预测值关系 Fig.6 Relationship between target value and predicted value of O phase thickness

本文以微观组织和力学性能预测的神经网络模型为基础，以Octave软件(兼容Matlab)为平台，编写了Ti₂AlNb合金构件组织和性能预测程序，并通过与有限元软件的结合，实现了Ti₂AlNb合金构件热成形- 热处理过程的全流程模拟。基于机器学习和有限元模拟的Ti₂AlNb合金构件全流程模拟的示意图如图 7所示，首先通过有限元模拟的方法对构件的成形过程进行模拟，将满足成形质量要求的模拟结果导入到Ti₂AlNb合金构件组织和性能预测程序，进行不同参数热处理后微观组织和力学性能的预测。其中有限元模拟采用哈尔滨工业大学流体高压成形技术研究所开发的Ti₂AlNb合金高温统一粘塑性本构模型用户子程序^[14]，该模型考虑了在变形过程中位错密度、晶粒尺寸和相含量等微观组织的演变，以及微观组织演变对流动应力的影响，具体建模过程和模型参数参见文献[14]。

图 Figure7(Fig.Figure7)

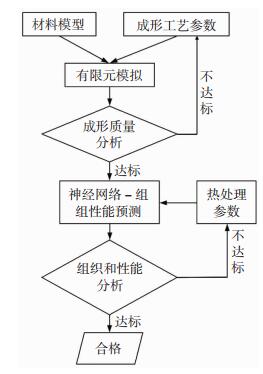
图 7 基于机器学习和有限元模拟的Ti2AlNb合金构件全流程模拟示意图 Fig.7 Schematic diagram of whole process simulation of Ti2AlNb alloy component based on machine learning and finite element simulation

本文采用上述方法对Ti₂AlNb合金管材的高温压制- 热处理工艺进行了全流程模拟和实验验证。高温压制是将管材加热到成形温度下，通过模具的合模动作对成形件施加载荷，使成形件发生塑性变形，成形出目标形状的构件。在管材的高温压制中，管坯的主要变形方式为弯曲变形。弯曲变形是高温变形中的一种常见变形方式。目标压制件截面尺寸为40 mm×40 mm，长度为60 mm。实验所采用管坯初始直径为44 mm，壁厚为2.4 mm，压制变形的上模总压下量为6.4 mm。模拟采用的模型和实验成形模具及成形件如图 8所示，成形温度为970 ℃，模拟选取的摩擦系数为0.3。

图 Figure8(Fig.Figure8)

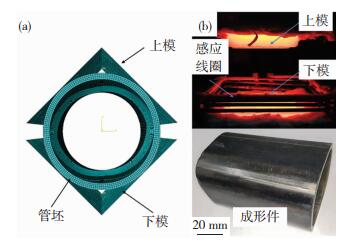
图 8 模拟模型(a)和成形模具及成形件(b) Fig.8 (a) Simulation model and (b) forming die and formed components

如图 9所示，成形结束时刻塑性等效应变和相对位错密度(其定义为ρ =1-ρ₀/ρ，其中，ρ为变形时刻的位错密度，ρ₀为初始时刻位错密度，该参数反应了在变形过程中位错密度的演变)的分布，构件各处圆角分布并不均匀，模具内侧圆角较大(图 9(a)两侧圆角)，而分模面处圆角较小(图 9(a)前后侧圆角)，这与实验件的圆角规律是一致的，模具与管坯之间的摩擦有利于材料向分模面处流动。成形件与模具接触部位和分模面圆角处应变较大。构件最大应变分布在管材圆角处。构件在变形过程中产生的位错密度分布与应变分布基本一致(如图 9(b)所示)，这是由于，在变形过程中，变形较大位置位错快速增殖，且成形时间短，位错来不及发生回复，在变形较大区域积累较多的位错。

图 Figure9(Fig.Figure9)

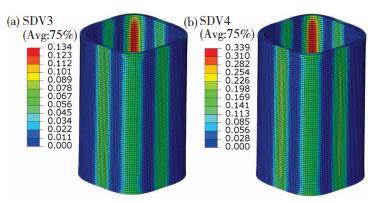
图 9 热态压制管成形结束时刻等效应变(a)和相对位错密度(b)分布 Fig.9 Distribution of (a) equivalent strain and (b) relative dislocation density of tube at the end of hot pressing and forming

图 10(a)和(b)为将970 ℃压制成形后管材进行810 ℃时效处理2 h后的屈服强度和O相片层厚度的模拟结果，该模型预测的Ti₂AlNb合金的屈服强度为650 ℃应变速率0.001 s^-1条件下的结果。

图 Figure10(Fig.Figure10)

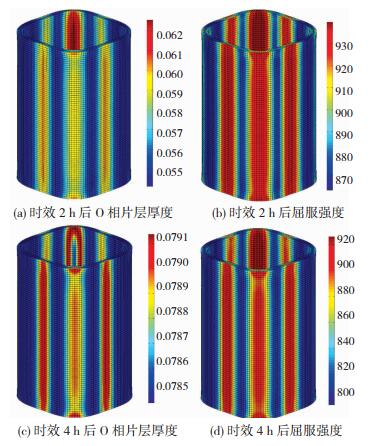
图 10 压制管材810 ℃时效后的O相片层厚度(单位：μm) 和650 ℃屈服强度(单位：MPa) Fig.10 Thickness of O phase and yield strength (650 ℃) of pressed tube after aging treatmentat 810 ℃: (a) thickness of O phase after aging treatment for 2 h; (b)yield strength after aging treatment for 2 h; (c)thickness of O phase after aging treatment for 4 h; (d)yield strength after aging treatment for 4 h

由图 10(a)和(b)可以看到，应变较大的区域，屈服强度和片层厚度略高。这是由于在应变较大区域，在变形过程中积累了更大的位错密度，在时效处理过程中，较高的位错和畸变能促进了O相的析出和长大。另外，在时效过程中，构件中的位错不能完全回复，位错强化导致变形较大区域仍有较高的强度。图 10(c)和(d)为970 ℃压制构件在810 ℃时效4 h后的O相片层厚度和屈服强度分布结果，可以看到，随着热处理时间的延长，构件的O相片层逐渐长大，屈服强度逐渐降低。如图 10(b)和(d)所示，随着时效时间的延长，构件的强度降低，这是由于，延长时效时间，O相片层宽度增加，位错密度降低。

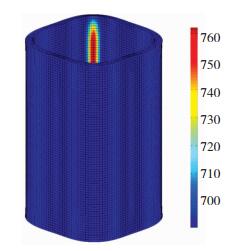
图 11为成形构件870 ℃时效4 h的屈服强度结果。如图 10(d)和图 11所示，随着时效温度的提高，构件的强度降低。这是由于，随着时效温度的提高，O相片层粗化和位错回复的速度增加。并且随着时效温度的提高，构件各处位错密度差异降低，由于位错强化导致的各处强度差异也随之降低，构件强度均匀性提高。

图 Figure11(Fig.Figure11)

图 11 压制构件在870 ℃时效4 h的屈服强度分布结果 Fig.11 Yield strength distribution of pressed component after aging treatment at 870 ℃ for 4 h

图 12为实验压制的构件进行810 ℃/2 h、810 ℃/4 h、870 ℃/2 h和870 ℃/4 h时效处理后所获得的微观组织形貌，取样位置为构件直壁区中间位置。

图 Figure12(Fig.Figure12)

图 12 压制构件经过(a)810 ℃/2 h，(b)810 ℃/4 h，(c)870 ℃/2 h和(d)870 ℃/4 h时效处理后的微观组织形貌 Fig.12 Microstructure of pressed components after aging treatment at (a) 810 ℃/2 h, (b) 810 ℃/4 h, (c) 870 ℃/2 h, and (d) 870 ℃/4 h

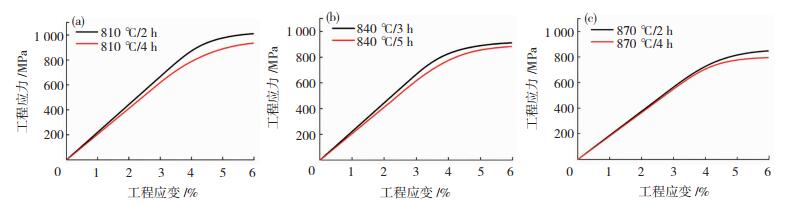
如图 12所示，时效处理后的组织为双态组织，片层的O相和等轴的α₂相分布在B2相基体上。随着时效时间的延长和时效温度的提高，O相片层逐渐长大。图 13为成形件经过不同温度和时间时效处理后的单向拉伸测试结果，拉伸试样的标距段尺寸为2 mm×2.4 mm×15 mm，取样位置为构件的中心位置，测试温度为650 ℃，应变速率为0.001 s^-1。如图 13所示，随着时效温度的提高和时效时间的延长，构件的强度逐渐降低。表 2为模拟结果与实验结果对比，可以看到模拟结果与实验结果的一致性较好。构件中O相片层的宽度随着时效时间的延长和和时效温度的提高而增加，屈服强度随着时效时间的延长和时效温度的提高而降低。

图 Figure13(Fig.Figure13)

图 13 压制构件在(a)810 ℃，(b)840 ℃和(c)870 ℃热处理后的单向拉伸应力应变曲线 Fig.13 Uniaxial tensile stress-strain curves of pressed components after heat treatment at (a) 810 ℃, (b) 840 ℃, and(c) 870 ℃

表2(Table 2)

表 2 不同热处理参数压制构件组织性能模拟结果与实验结果对比 Table 2 Comparison between simulation results and experimental results of microstructure and mechanical properties of pressed components with different heat treatment parameters 热处理参数 模拟片层厚度/μm 实验片层厚度/μm 模拟屈服强度/MPa 实验屈服强度/MPa 810 ℃/2 h 0.059 0.07 903 921 810 ℃/4 h 0.079 0.09 866 794 840 ℃/3 h 0.116 0.11 768 808 840 ℃/5 h 0.160 0.14 712 762 870 ℃/2 h 0.124 0.12 741 748 870 ℃/4 h 0.181 0.17 693 722

表 2 不同热处理参数压制构件组织性能模拟结果与实验结果对比 Table 2 Comparison between simulation results and experimental results of microstructure and mechanical properties of pressed components with different heat treatment parameters

本文基于机器学习的方法，建立了考虑预变形影响的成形构件时效处理组织和力学性能预测神经网络模型，并通过与有限元软件的结合，实现了Ti₂AlNb合金构件热成形- 热处理过程的全流程模拟和构件的组织- 性能预测。

通过该方法对Ti₂AlNb合金管材的高温压制- 热处理工艺进行了模拟。在构件大应变区域，变形产生的位错密度更高，在时效处理中，在应变较大的区域O相的片层宽度更大，屈服强度更高。随着时效温度的提高和时效时间的延长，构件中O相片层逐渐粗化，屈服逐渐降低。成形构件在时效处理后，构件各处的微观组织和力学性能并不均匀，提高时效温度有利于提高构件各处强度的均匀性。实验验证表明，模拟结果与实验结果一致性较好。

通过将机器学习与有限元模拟的结合，可以实现构件热成形- 热处理工艺的微观组织和力学性能预测，并可以通过模拟分析成形和热处理参数对构件变形、微观组织和力学性能的影响，指导成形和热处理工艺优化。