普通铝合金模量较低,易磨损等缺点限制了其在工业领域的应用。铝基复合材料则具有高比强度、高比模量、尺寸稳定性好等优异性能,可以很好的代替普通铝合金[1],因而在航天航空和汽车领域得到广泛应用。传统的增强体按形态可分为颗粒、晶须和纤维增强体等,但Al2O3等传统陶瓷增强相固有的脆性使复合材料本身的塑性严重下降,无法满足工程应用的需求[2]。于是各种碳质增强体被作为增强体而使用,碳质增强体按形态可分为零维的富勒烯、一维的碳纳米管(CNT)、纳米碳纤维(CNF)、二维的石墨烯(Gr)等[3]。其中,石墨烯作为一种新型的纳米增强体,以其杰出的性能,如高拉伸性能(130 GPa),高弹性模量(1 TPa),优异的热传导性(导热系数5.3 kW ·m-1 ·K-1) 而成为最具潜力的铝基复合材料增强体[4]。石墨烯增强铝基复合材料可作为结构材料应用于航空航天、汽车和运输行业,能够满足当代工业对材料轻质高强的需求。目前,石墨烯增强铝基复合材料的制备方法和其热变形行为正广受关注。针对石墨烯作为增强体的铝基复合材料的研究主要集中在制备方法上,还有许多问题尚未得到解决,如石墨烯在基体中易团聚,容易与基体发生界面反应等[5],均有待进一步的研究。热变形过程中材料的流动行为通常是复杂的,其中加工硬化和动态软化现象都受到变形参数,如应变速率、温度的显著影响[6]。而本构方程可以将材料的流变应力和热力参数联系起来,用应变补偿的Arrhenius equation(双曲正弦函数)本构模型可以精确预测铝及铝合金的热变形行为[7-9]。
本文研究了变形参数对粉末冶金法制备的石墨烯增强铝基复合材料热压缩过程中流动应力的影响,建立了复合材料的本构方程,并分析其变形机理。此外,还分析了石墨烯增强铝基复合材料在热变形行为中的微观结构演变,以期为优化制定石墨烯增强铝基复合材料的塑性变形工艺提供必要指导。
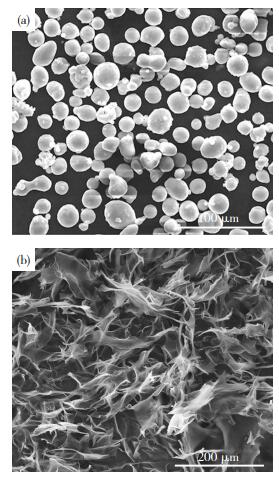
1 实验 1.1 实验材料本实验所用纯铝粉末的纯度为99.97%,其化学成分见表 1。图 1为纯铝粉末的SEM形貌,可以看到,纯铝颗粒大小均匀,呈球状,平均粒径为33 μm。本实验中石墨烯的添加量为0.5%(质量分数,下同)。图 1(b)为Hummers法制备的氧化石墨烯的SEM图,可以看到,氧化石墨烯呈薄片状,表面有许多褶皱和卷曲。
| 表 1 纯Al粉末化学成分表(质量分数/%) Table 1 Chemical composition of pure Al powder(wt.%) |
|
图 1 纯铝粉末(a)及氧化石墨烯(b)的SEM图 Fig.1 SEM images of pure aluminum powder (a) and graphene oxide (b) |
本文采用粉末冶金法制备石墨烯增强铝基复合材料。按0.5wt. %比例称取氧化石墨烯加入乙醇溶液中超声波分散1 h,再将称取的铝粉加入到混合溶液中,放入球磨罐中,抽真空后冲入氩气,再放入低温粉末破碎机中球磨1 h(球料比40∶1,转速为200 r/min)。将球磨后的混合溶液放入真空干燥箱干燥12 h,得到复合粉体,其形貌见图 2,可以看到氧化石墨烯均匀的分布在铝颗粒周围。

|
图 2 氧化石墨烯和纯铝球磨后的复合粉体SEM图 Fig.2 SEM image of composite powder of graphene oxide and pure aluminum after ball milling |
将复合粉体倒入石墨模具,并放入烧结炉中进行预压,预压1次后加入石墨垫块,以增加压头的行程。而后在烧结炉中通入还原气体氩气,将预制样在580 ℃、70 MPa条件下进行热压烧结,烧结成品的尺寸为Φ18 mm×50 mm,如图 3(a)所示。用线切割将棒材加工成Φ8 mm×12 mm的圆柱形压缩试样,如图 3(b)所示。

|
图 3 石墨烯增强铝基复合材料(a)和等温压缩样品(b) Fig.3 Graphene-reinforced aluminum matrix composites (a) and isothermal compression samples (b) |
采用Gleeble 3800热模拟机对复合材料进行等温压缩实验,变形温度300~450 ℃,应变速率为0.01~1 s-1,变形量为75%。将试样按照10 ℃/s的升温速率加热到设定温度并保温5 min,以保证试样温度分布均匀。在样品两端的凹槽内填充石墨润滑剂,以减小摩擦对试验过程的影响。
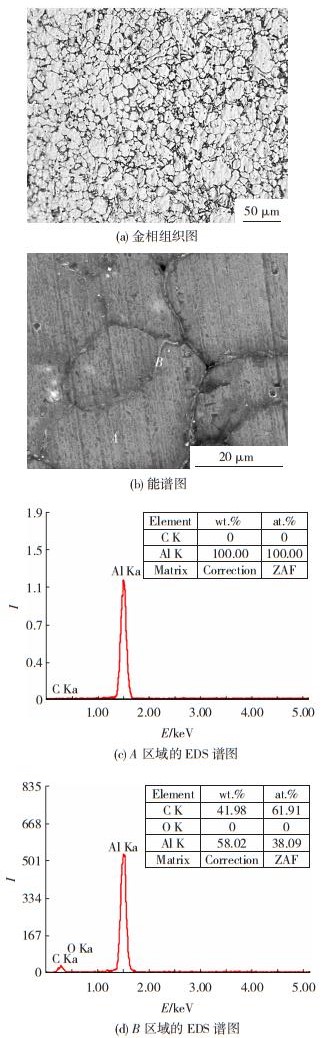
2 结果与分析 2.1 石墨烯增强铝基复合材料的微观组织观察图 4(a)和(b)是石墨烯增强铝基复合材料的金相组织和SEM形貌,可以看出,粉末冶金法制备的石墨烯增强铝基复合材料晶粒呈圆形或椭圆形,大小均匀且无明显的孔洞。为考察复合材料中的元素分布,对复合材料进行了EDS分析,结果如图 4(c)和(d)所示,可以看到,复合材料中只有Al和C两种元素,区域A为铝基体,该区域只有Al铝元素的特征峰,未出现石墨烯。区域B(晶界)具有Al和C的特征峰,表明石墨烯均匀分布在晶界处。EDS谱图中没有O峰,这表明在制备过程中复合材料未出现氧化现象。
|
图 4 石墨烯增强铝基复合材料的金相组织和能谱图 Fig.4 Metallographic structureand energy spectrum of graphene-reinforced aluminum matrix composites: (a) metallographic structure; (b) energy spectrum; (c) EDS plot of region A; (d) EDS plot of region B |
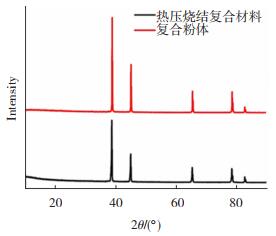
石墨烯增强铝基复合粉体和复合材料的XRD谱如图 5所示。
|
图 5 石墨烯增强铝基复合粉体和复合材料的XRD谱图 Fig.5 XRD of graphene-reinforced aluminum matrix composite powders and composites |
由图 5可以看到,复合粉体中只有Al的特征峰,未出现氧化石墨烯的特征峰,这可能是由于石墨烯加入的量太少而难以检测。热压烧结后的复合材料XRD谱图与烧结前相同,表明烧结过程未发生晶体结构的改变,且XRD谱中没有Al4C3的衍射峰,表明增强相石墨烯和铝基体未发生明显界面反应。
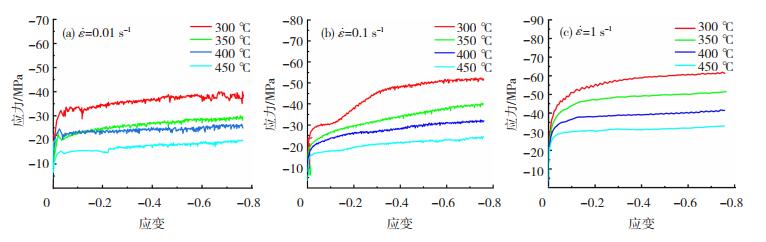
2.2 石墨烯增强铝基复合材料的应力-应变曲线由图 6可知,在变形初期石墨烯增强铝基复合材料的流变应力随着应变的增大而急剧上升,这是由于外加应力使得位错发生缠结、堆积产生应力集中,同时增强体石墨烯在晶界处钉扎,阻碍了位错的运动。随着变形程度的进一步增加,材料软化作用逐渐增强,动态软化和加工硬化竞争效果逐渐达到动态平衡,流变应力缓慢上升至峰值后逐渐稳定,从而进入稳态流变状态。且由图 6可得,进入稳态流变状态后,材料的流变应力决定于变形温度或应变速率。因此,石墨烯增强铝基复合材料的软化机制以动态回复为主。
|
图 6 复合材料在不同应变速率下的真应力-应变曲线 Fig.6 True stress-strain curves of composites at different strain rates |
本构方程的建立可以评估复合材料的热变形行为,应变速率、变形温度和流变应力之间的关系被广泛应用于Arrhenius方程,其表达式为[10]
| $ \mathit{\dot \varepsilon }{\rm{ = }}A{\mathit{\sigma }^{\mathit{n}{\rm{1}}}}{\rm{exp}}\left( { - Q/RT} \right), \mathit{\alpha \sigma } < 0.8 $ | (1) |
| $ \mathit{\dot \varepsilon }{\rm{ = }}A{\rm{exp}}\left( {\mathit{\beta \sigma }} \right){\rm{exp}}\left( {-Q/RT} \right), \mathit{\alpha \sigma } > 1.2 $ | (2) |
| $ \mathit{\dot \varepsilon }{\rm{ = }}A{\left[ {\sinh \left( {\mathit{\alpha \sigma }} \right)} \right]^n}{\rm{exp}}\left( { - Q/RT} \right), 对所有应力 $ | (3) |
式中:Q是热变激活能,kJ/mol;
| $ \mathit{Z} = \mathit{\dot \varepsilon }{\rm{exp}}\left( {Q/RT} \right) = A{\left[ {\sinh \left( {\mathit{\alpha \sigma }} \right)} \right]^n} $ | (4) |
对公式(1)和(2)两边取对数可得
| $ \rm{In}\mathit{\dot \varepsilon } = \rm{In}\mathit{A}{\rm{ + }}{\mathit{n}_1}In\mathit{\sigma - }\mathit{Q}/\mathit{RT} $ | (5) |
| $ \rm{In}\mathit{\dot \varepsilon } = \rm{In}\mathit{A} + \mathit{\beta \sigma - }\mathit{Q}/\mathit{RT} $ | (6) |
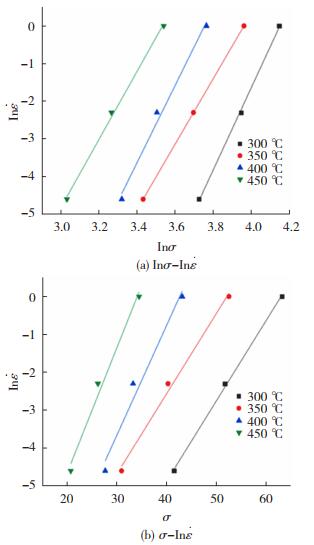
将不同变形条件下的流变应力和所对应的应变速率带入公式(5)和(6), 然后绘制Inσ-In
|
图 7 不同变形温度下应变速率与流变应力和对数流变应力的关系曲线 Fig.7 Relationship between strain rate, flow stress, and logarithmic flow stress at different deformation temperatures |
对式(3)两边取自然对数得到式(7),并对式(7)中的1/T求偏导数可得,
| $ \mathit{Q}/\mathit{RT} = \rm{In}\mathit{A} - \rm{In}\mathit{\dot \varepsilon }{\rm{ + }}{\mathit{n}_2}\rm{In}\left[ {\sinh \left( {\mathit{\alpha \sigma }} \right)} \right] $ | (7) |
| $ Q = R{n_3}S $ | (8) |
| $ {n_3} = {\left\{ {\frac{{\partial \rm{In}\mathit{\dot \varepsilon }}}{{\partial \rm{In}\left[ {\sinh \left( {\mathit{\alpha \sigma }} \right)} \right]}}} \right\}_T} $ | (9) |
| $ S = {\left\{ {\frac{{\partial \rm{In}\left[ {\sinh \left( {\mathit{\alpha \sigma }} \right)} \right]}}{{\partial \left( {1\;000} \right)/T}}} \right\}_{\mathit{\dot \varepsilon }}} $ | (10) |
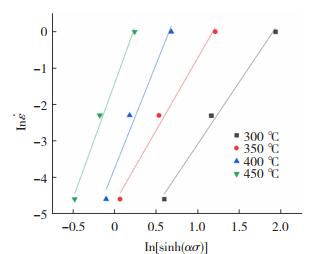
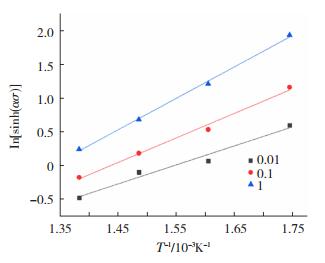
由式(9)可以发现,当变形温度不变时,In[sinh(ασ)]-In${\mathit{\dot \varepsilon }} $呈线性关系,且令其斜率为n2,将相应的值带入绘制的In[sinh(ασ)]-In${\mathit{\dot \varepsilon }} $曲线并进行线性回归,可得n2= 6.461 42,再将n2的值带入α2=β/n2,可得α2值为0.027 66。在一定应变速率下,T-1/10-3K-1-In[sinh(ασ)]呈线性关系,且令其斜率为S。将调整后的α2带入式(8)中,绘制如图 8、9所示的In[sinh(ασ)]-In${\mathit{\dot \varepsilon }} $和T-1/10-3K-1-In[sinh(ασ)]图,可得n3=5.503 76;S值是取图 9中3条直线斜率的平均值,得S= 2.851 74。则热变激活能Q=Rn3S= 130.427 99 kJ/mol。
|
图 8 不同变形温度下应变速率与流变应力的关系曲线 Fig.8 Relationship between strain rate and flow stress at different deformation temperatures |
|
图 9 不同应变速率下流变应力与变形温度的关系曲线 Fig.9 Relationship between flow stress and deformation temperature at different strain rates |
对式(4)Z=${\mathit{\dot \varepsilon }} $exp(Q/RT)=A[sinh(ασ)]n两边取对数可得
| $ \rm{In}\mathit{Z}{\rm{ = }}\rm{In}\mathit{\dot \varepsilon } + \mathit{Q}/\mathit{RT} $ | (11) |
| $ \rm{In}\mathit{Z}{\rm{ = }}\rm{In}\mathit{A} + \mathit{n}\left[ {\sinh \left( {\mathit{\alpha \sigma }} \right)} \right] $ | (12) |
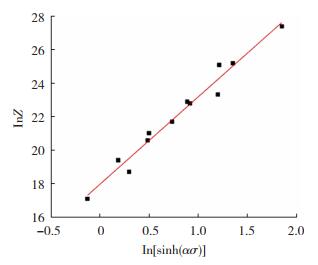
给${\mathit{\dot \varepsilon }} $、Q和T赋值可以得出对应的InZ,绘制In[sinh(ασ)]和InZ图如图 10所示,且InA是直线In[sinh(ασ)]和InZ在坐标轴上的截距,可得A=6.400 101×107。将计算出的材料常数带入式(3)可以得到石墨烯增强铝基复合材料的本构方程,
| $ \begin{array}{l} \mathit{\dot \varepsilon = }{\rm{6}}{\rm{.400}}\;{\rm{101 \times 1}}{{\rm{0}}^{\rm{7}}}{\left[ {\sinh \left( {0.033\;2274\mathit{\sigma }} \right)} \right]^{5.503\;765}} \cdot \\ {\rm{exp}}\left( { - \frac{{130\;427.99}}{{8.31T}}} \right) \end{array} $ | (13) |
|
图 10 InZ和In[sinh(ασ)]的关系曲线图 Fig.10 Relationship between InZ and In[sinh(ασ)] |
在进行铝基复合材料的热变形机制研究时,通常认为n的大小对应不同的变形机制,n=2,晶界滑动;n=3,黏滞滑移;n=5,高温位错攀移;n=8,晶格扩散控制的蠕变[12-14]。本文计算的石墨烯增强铝基复合材料的应力指数n=5.503 765,这表明该复合材料的变形机制为位错攀移。
热变激活能Q是一个非常重要的物理参数,它表示材料在热变形时位错在滑移面上滑移所需克服的能量势垒,Q值越高表明材料在热变形时克服变形抗力所需要的能量越大[15],更不易于材料的塑性成型加工。Mokdada等[16]用球磨和热压烧结进行热挤压制备出的2.0%CNT/2024Al纳米复合材料的热变激活能为322.3 kJ/mol,Guo[17]等用机械球磨结合放电等离子烧结制备的VGCNF/Al复合材料的热变激活能为248.58 kJ/mol。可见,与其他的碳增强体如碳纳米管(CNT)、碳纳米纤维增强的铝基复合材料相比,本文制备的石墨烯增强铝基复合材料热变激活能更低,更容易发生塑性变形。
纯铝的点阵自扩散激活能为144 kJ/mol,晶界自扩散激活能为72 kJ/mol[18],本文计算出的石墨烯增强铝基复合材料的热变激活能介于两者之间,所以该复合材料的变形机制为点阵自扩散。
图 11为复合材料在400 ℃热压缩后的形貌,可以发现晶粒在热变形后呈长条纤维状,石墨烯分布在铝基体的晶界处,与基体接触面积增大。石墨烯表面存在许多褶皱,呈卷曲折叠的薄片状结构,在受压过程中存在一个褶皱舒展平铺的过程[19],这有助于提高位错的变形协调性[2, 20-24]。

|
图 11 400 ℃下等温压缩后石墨烯增强铝基复合材料的SEM形貌 Fig.11 SEM image of graphene-reinforced aluminum matrix composite after isothermal compression at 400 ℃ |
图 11的研究结果表明,在铝基体中加入适量的(≤0.5%) 石墨烯,不会因为增强相的引入而导致塑性降低的现象,而这一现象在传统金属基复合材料中是普遍存在的[25]。
3 总结1) 采用湿混球磨结合真空热压烧结的方法成功制备了0.5%石墨烯增强铝基复合材料,SEM和XRD谱图结果表明添加的石墨烯未与铝基体发生明显的界面反应。
2) 0.5%石墨烯增强铝基复合材料在热变形过程中具有稳态流变特征,且动态回复为主要的软化机制。基于Arrhenius方程计算获得了石墨烯增强铝基复合材料热变激活能为130.427 99 kJ/mol,其本构方程为
| $ \begin{array}{l} \mathit{\dot \varepsilon = }{\rm{6}}{\rm{.400}}\;{\rm{101 \times 1}}{{\rm{0}}^{\rm{7}}}{\left[ {\sinh \left( {0.033\;2274\mathit{\sigma }} \right)} \right]^{5.503\;765}} \cdot \\ {\rm{exp}}\left( { - \frac{{130\;427.99}}{{8.31T}}} \right) \end{array} $ |
3) 石墨烯增强铝基复合材料的应力指数n=5.503 76,这表明该复合材料的变形机制为位错攀移。在热变形过程,与其他的碳基增强体(碳纳米管、碳纤维)相比,石墨烯增强铝基复合材料的热变激活能更低。
| [1] |
ZHAO Zhanyong, BAI Peikang, DU Wenbo, et al. An overview of graphene and its derivatives reinforced metal matrix composites: Preparation, properties and applications[J]. Carbon, 2020, 170: 302-326. DOI:10.1016/j.carbon.2020.08.040 |
| [2] |
张丁月. 石墨烯增强铝基复合材料的非均匀变形行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. ZHANG Dingyue. Research on non-uniform deformation behavior of graphene-reinforced aluminum matrix composites[D]. Harbin : Harbin Institute of Technology, 2019. DOI: 10.27061/d.cnki.ghgdu.2019.003039 |
| [3] |
ÖMER Güler, NIHAL Baǧc. A short review on mechanical properties of graphene reinforced metal matrix composites[J]. Journal of Materials Research and Technology, 2020, 9(3): 6808-6833. DOI:10.1016/j.jmrt.2020.01.077 |
| [4] |
YU H, ZHANG S Q, XIA J H, et al. Microstructural evolution, mechanical and physical properties of graphene reinforced aluminum composites fabricated via powder metallurgy[J]. Materials Science and Engineering: A, 2021, 802: 140669. DOI:10.1016/j.msea.2020.140669 |
| [5] |
高一波. 石墨烯增强铝基复合材料的制备及其性能研究[D]. 太原: 中北大学, 2019. GAO Yibo. Research on propertier and preparation of graphene reinforced aluminum matrix composite[D]. Taiyuan: North University of China, 2019. |
| [6] |
REZAEI ASHTIANI H R, SHAHSAVARI P. Constitutive modeling of flow behavior of precipitation-hardened AA7022-T6 aluminum alloy at elevated temperature[J]. Transactions of Nonferrous Metals Society of China, 2020, 30(11): 2927-2940. DOI:10.1016/S1003-6326(20)65432-2 |
| [7] |
WANG Han, ZHANG Haiming, CUI Zhenshan, et al. Compressive response and microstructural evolution of in-situ TiB2 particle-reinforced 7075 aluminum matrix composite[J]. Transactions of Nonferrous Metals Society of China, 2021, 31(5): 1235-1248. DOI:10.1016/S1003-6326(21)65574-7 |
| [8] |
AJAY C, NIHAARIKHA G N, HIRAJITH D S, et al. Constitutive analysis of homogenized 7005 aluminum alloy at evaluated temperature for extrusion process[J]. Materials & Design, 2014, 66: 129-136. DOI:10.1016/j.matdes.2014.10.045 |
| [9] |
MA K, LIU Z Y, ZHANG X X, et al. Hot deformation behavior and microstructure evolution of carbon nanotube/7055Alcomposite[J]. Journal of Alloys and Compounds, 2021, 854: 157275. DOI:10.1016/j.jallcom.2020.157275 |
| [10] |
SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138. DOI:10.1016/0001-6160(66)90207-0 |
| [11] |
ZENER C, HOLLOMON J H. Effect of strain-rate upon the plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22-27. DOI:10.1063/1.1707363 |
| [12] |
MOHAMED F A, PARK K T, LAVERNIA E J. Creep behavior of discontinuous SiC-Al composites[J]. Materials Science & Engineering A, 1992, A150: 21. DOI:10.1016/0921-5093(90)90004-M |
| [13] |
PARK K T, LAVERNIA E J, MOHAMED F A. High-temperature deformation of 6061 Al[J]. Acta Metall Mater, 1994, 42: 667. DOI:10.1016/0956-7151(94)90264-X |
| [14] |
LI Y, NUTT S R, MOHAMED F A. An investigation of creep and substructure formation in 2124 Al[J]. Acta Mater, 1997, 45: 2607. DOI:10.1016/S1359-6454(96)00367-9 |
| [15] |
陈欣荣. Al-7Si/(10SiCp+xTiB2)混杂增强铝基复合材料高温流变行为研究[D]. 长沙: 湖南大学, 2019. CHEN Xinrong. High temperature deformation behavior of Al-7Si/(10SiCp+xTiB2) hybrid composites[D]. Changsha: Hunan University, 2019. DOI: 10.27135/d.cnki.ghudu.2019.000006 |
| [16] |
MOKDAD F, CHEN D L, LIU Z Y, et al. Hot deformation and activation energy of a CNT-reinforced aluminum matrix nanocomposite[J]. Materials Scienceand Engineering: A, 2017, 17: 322-331. DOI:10.1016/j.msea.2017.04.006 |
| [17] |
GUO Y, LIU X G, XU Z F, et al. Effect of VGCNF on high-temperature deformation performance and softening mechanism of aluminum matrix[J]. Journal of Alloys and Compounds, 2020, 818: 152923. DOI:10.1016/j.jallcom.2019.152923 |
| [18] |
LI M, LIU Y, WU S, et al. Superplastic deformation of duralumin LY12CZ under an electric field[J]. Journal of Materials Processing Technology, 1994, 40: 385-93. DOI:10.1016/0924-0136(94)90463-4 |
| [19] |
YAN S J, DAI S L, ZHANG X Y. Investigating aluminum alloy reinforced by graphene nanoflakes[J]. Material Science and Engineering A, 2014, 61: 440. DOI:10.1016/j.msea.2014.06.077 |
| [20] |
XU ZY, LI CJ, WANG Z, et al. Balancing the strength and ductility of graphene oxide-carbon nanotube hybrid reinforced aluminum matrix composites with bimodal grain distribution[J]. Materials Science and Engineering: A, 2020, 796: 140067. DOI:10.1016/j.msea.2020.140067 |
| [21] |
FENG Siwen, GUO Qiang, LI Zan, et al. Strengthening and toughening mechanisms in graphene - Al nanolaminated composite micro-pillars[J]. Acta Materialia, 2017, 125: 98-108. DOI:10.1016/j.actamat.2016.11.043 |
| [22] |
刘志颖, 郭强, 张荻. 微纳叠层金属复合材料的断裂性能研究[J]. 中国材料进展, 2018, 37(2): 138-146. LIU Zhiying, GUO Qiang, ZHANG Di. The fracture property in micro/nano-laminated metal composites[J]. Materials China, 2018, 37(2): 138-146. DOI:10.7502/j.issn.1674-3962.2018.02.09 |
| [23] |
于真鹤. 多层石墨烯/6063Al复合材料强韧化设计及断裂行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2021. YU Zhenhe. Research on strengthening and toughening design and fracture behaviors of multilayer graphene/6063Al composite[D]. Harbin: Harbin Institute of Technology, 2021. DOI: 10.27061/d.cnki.ghgdu.2021.000216 |
| [24] |
WU Gaohui, YU Zhenhe, JIANG Longtao, et al. A novel method for preparing graphene nanosheets/Al composites by accumulative extrusion-bonding process[J]. Carbon, 2019, 152: 932-945. DOI:10.1016/j.carbon.2019.06.077 |
| [25] |
李炯利, 王旭东, 武岳, 等. 石墨烯含量对铝基复合材料微观组织和力学性能的影响[J]. 稀有金属, 2018, 42(3): 252-258. LI Jiongli, WANG Xudong, WU Yue, et al. Microstructure and mechanical properties of aluminum-matrix composite with different graphene contents[J]. Chinese Journal of Rare Metals, 2018, 42(3): 252-258. DOI:10.13373/j.cnki.cjrm.xy16100019 |
 2022, Vol. 30
2022, Vol. 30


