节能减排是汽车制造领域的发展趋势。由于铝合金材料具有比强度高、抗腐蚀、可回收利用等特点,越来越多的钢制汽车零部件被铝合金材料代替,汽车行业呈全铝化发展趋势[1-2]。铝合金的成型需经过如轧制、挤压、拉拔等塑性加工过程,材料在加工过程中根据能量最低原理,各类微观机制竞争导致其出现PLC效应[3-4]、各向异性[5-6]、Roping效应[7-8]等,这给材料使用与推广带来巨大困难。要解决材料使用瓶颈,推动产品更新换代,最核心的问题是了解其微观机理,从微观组织调控宏观性能,推动材料产业化应用。王正安等[9]在不同退火时间及温度下研究了固溶Mg原子与位错相互作用理论,为高镁铝合金热变形产品质量改善提供理论和实验依据,研究发现,铝合金中大量析出相的存在能够引起反常PLC效应[10]。Leora等[11]利用时间分辨暗场X光成像技术在微米尺度上观察到位错线性钉扎现象,并解释了位错钉扎与滑移重组的微观机理,而溶质原子的数量能够影响位错的钉扎力度[12],并与激活能有密切关联[13]。塑性变形容易导致材料出现各向异性,为克服材料各向异性,进而提高其宏观成型性能,多项研究从织构入手,试图找到微观织构成因及其演化规律,建立微观织构与宏观性能的关系。研究认为,通过改变中间退火工艺或时效工艺,可以有效减小制耳率,提高材料使用效率[14-16],选择不同的轧制方式也可以调控各织构百分比,从而改善材料成形性能[17]。以上文献多集中于材料在变形过程中单一效应或现象的应用和机理问题研究,但由塑性变形理论和晶体动力学可知,材料在变形过程中,多种微观机制存在竞争现象。迄今为止,关于材料在塑性变形过程中其内部微观组织演化和竞争规律的研究尚鲜有报道。拉伸试验是研究铝合金材料力学性能最核心的试验方法,其过程包含材料弹性变形、塑性变形等。现阶段,研究晶粒取向的手段有两种,电子背散射衍射(EBSD)微观织构法和XRD宏观织构法,与EBSD法相比,XRD法具有更强的统计意义,对样品的统计量高出约4~6个数量级,而原位XRD法与非原位相比,织构含量计算的准确度得到进一步提高,织构测试和含量百分比计算重复性可精确到小数点后两位,是研究材料在不同应变下织构演化规律的重要手段。目前,将原位拉伸XRD法用于对织构的研究尚未见于报道。本文将通过原位拉伸与XRD实验相结合,从宏观现象与微观组织的关系出发,研究样品在不同应变下样品内部的晶格变化、PLC效应以及织构的变化和竞争规律,以期为材料的宏观变形和微观晶格应变、PLC效应、织构演化等机理问题提供数据支持。
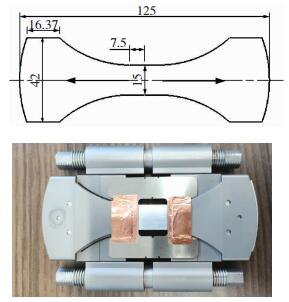
1 实验样品为商用3004铝合金薄板,化学成分(质量分数):Mn:1.11%, Mg: 1.21%, Fe: 0.51%, Si: 0.25%, Zn: 0.03%, Cu: 0.1%, 余量Al。板厚0.5 mm,经350 ℃,2 h退火处理。样品尺寸见图 1,平行段长15 mm,宽15 mm,平行段区域为样品X射线照射区域, 常规拉伸试验在日本岛津100 kN电子拉伸试验机上进行,原位拉伸试验在本文作者所在团队自主开发的离线式原位拉伸装置上进行。离线式原位拉伸装置可对样品进行有效夹持,在定量拉伸时原位拉伸装置放置于加载系统上进行拉伸,拉伸完毕,原位拉伸装置放置于XRD样品台进行宏观织构和物相测试。拉伸速率为2 μm/s。样品轧制方向、拉伸方向与样品长度方向一致,如图 1箭头所示。XRD测试仪型号:帕纳科锐影,X射线源为铜靶,索拉狭缝为2.29°,织构测试光斑2 mm×2 mm,正交准直器0.27°。通过无织构标准铝合金样品进行散焦校正。
|
图 1 拉伸试样尺寸图(a)和原位拉伸装置(b)(单位:mm) Fig.1 Dimension of tensile test sample (a) and image of in-situ strain apparatus(b) |
为确定样品弹性变形区、PLC效应区等所对应的变形量位置,在轧板的同一区域取样品A和B,两个样品为平行样。首先对样品A在电子拉伸试验机上进行常规拉伸试验,然后对样品B进行原位拉伸试验,原位拉伸试验时每增加一定变形量,对样品进行XRD物相测试,并计算晶格常数。在初始状态、弹性变形区、初始塑性变形区、PLC效应区、PLC效应弱化区、近断裂区分别进行XRD织构测试。在不同的应变下,织构数据标记如下:原始状态:T0;弹性变形区:T1;初始塑性变形区:T2;PLC效应区:T3;PLC效应弱化区: T4;近断裂区: T5、T6。
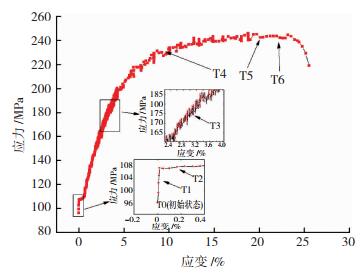
2 结果分析与讨论 2.1 常规拉伸试验分析样品A常规拉伸试验测试结果如图 2所示。根据样品的应变行为可将样品分为弹性变形区、初始塑性变形区、PLC效应区、PLC效应弱化区、近断裂区。在弹性变形区,应力应变曲线呈线性关系;在初始塑性变形区,应力应变曲线出现平台;在PLC效应区,应力应变曲线呈现锯齿形屈服行为;在PLC效应弱化区,锯齿屈服行为减弱;在近断裂区,应力应变曲线趋于光滑。
|
图 2 常规拉伸试验应力-应变曲线 Fig.2 Strain-stress curve of normal tensile test |
确定样品各阶段发生的应变位置后,利用原位拉伸试验装置对第2个样品进行原位拉伸试验,对其进行XRD物相测试并选取(111), (200), (220)的3个衍射面进行织构测试。
2.2 原位拉伸试验分析利用原位拉伸试验装置对不同应变下获得的XRD (422)衍射峰物相数据进行晶格常数计算,计算结果如图 3所示。由图 3可以看到,样品在弹性变形区,晶格常数直线减小,在塑性变形区,其减小趋势脱离线性,晶格应变伴随整个试验过程。

|
图 3 应变与晶格常数的关系曲线 Fig.3 Relationship between strain and lattice parameter |
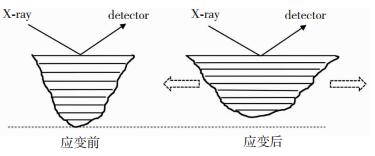
X射线衍射仪获取数据的几何关系可解释晶格常数减小的原因。如图 4所示,入射X射线与衍射X射线所在平面与样品表面垂直,能够参与衍射的晶面与样品表面平行,由材料不可压缩原理可知,晶格常数沿水平方向被拉长,垂直方向则必然在拉力作用下减小。样品断裂后,晶格常数未恢复至初始位置,表明样品断裂后其内部仍存在部分残余应力。晶格常数在拉伸过程中的变化规律可为材料塑性变形本构方程提供晶格应变的试验支撑。
|
图 4 晶格应变示意图 Fig.4 Schematic diagram of lattice parameter variation |
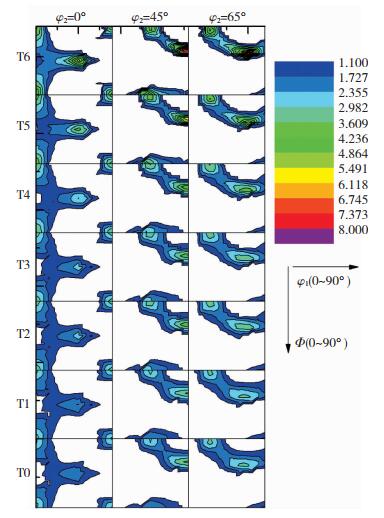
为分析织构在拉伸过程中的变化情况,借助labotex软件, 利用ADC[18-20]计算方法计算并绘制晶粒取向分布(ODF)图。在欧拉空间内表征织构分布状态,晶体取向可用3次转动表示, 在右手定则直角坐标系内第1次转动为晶体绕Z轴逆时针转动角度记作φ1,第2次转动为晶体绕X轴逆时针转动角度记作Φ,第3次转动为晶体绕Z轴逆时针转动角度记作φ2,每组欧拉角(φ1,Φ,φ2)表示晶体3次转动所到达的晶体取向。每次织构测试完成后,选取φ2=0°, 45°, 65°的ODF数据对织构进行绘图,该作图方式能够满足铝合金6种典型织构分析需求。从图 5可以看出,样品表现出典型的部分再结晶退火状态。立方织构和典型冷轧织构共存,T0、T1织构等高线分布和强度未发生变化,表明织构未参与弹性形变拉伸过程。样品在弹性应变区,衍射峰(422)峰位随着应变ε的增加开始向高角度移动,但形状和半高宽均未发生变化,表明在拉力作用下,样品内部产生了宏观应力,该应力存在于多个晶体尺度范围内,这种宏观应力在XRD物相上的表现为峰位漂移[21]。
|
图 5 不同应变下样品的ODF分布图 Fig.5 ODF distribution of sample under different strain |
图 3和图 5数据表明,在拉伸试验过程中,晶格应变所需的能量最小,在此阶段晶格行为类似弹簧,而其“刚度”与固溶度、晶粒大小、边界有关。利用原位拉伸装置可排除样品中晶粒大小和边界因素,为在弹性变形区研究晶格应变行为,提供了一种利用晶格应变手段研究材料固溶度的新思路。在图 5中,T2为样品初始塑性变形区ODF分布图,与T0、T1相比,织构等高线分布和强度未发生明显变化,表明在此阶段织构仍未参与样品变形过程。从图 6可知,在PLC效应区,T3织构总量最少,此现象归因于6种典型织构内部位错增多,晶格畸变加剧,部分晶粒的衍射晶胞完整性遭到破坏,晶粒X射线衍射信号减弱。随着拉伸试验持续,参与PLC效应的Mg原子逐渐减少,导致PLC效应弱化,表现为应力应变曲线锯齿现象减弱,此行为可从图 2得到证实。从图 5中的T4、T5、T6织构分布图可以看到,等高线形状和分布状态未发生明显变化,但强度显著增加,表明样品内织构总量在此应变区域增加,这一结果从图 6的计算数据也可以得到进一步证实。
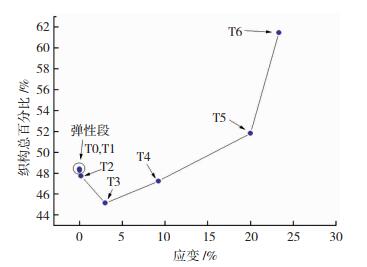
|
图 6 不同应变下6种典型织构总百分比 Fig.6 Overall percentage of six typical textures under different strain |
由图 7可知,在T4、T5、T6区域,织构总量和各织构分量随着应变的增加而增加,并且在整个拉伸过程中,6种典型织构随应变的走势保持一致,表明大量随机取向开始向6种典型织构靠拢,通过前述分析可推测,与晶格应变、PLC效应相比,晶粒取向转动所需能量最大。
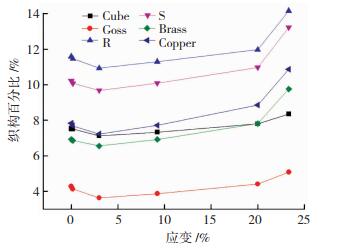
|
图 7 不同应变下6种典型织构百分比 Fig.7 Percentage of six typical textures under different strain |
图 8为(422)衍射峰物相数据,此衍射峰的位移和形状变化证实材料内部宏观应力与微观应力的共存行为。衍射峰的位移可由宏观应力解释,半高宽的变化可由微观应力解释。衍射峰半高宽在变形量25 μm处(T2织构)开始增加,表明晶粒内部开始出现微观应力,在其作用下位错密度增加,并产生滑移、重组[22],为产生PLC效应积累位错量和滑移所需能量。晶格常数持续减小,表明宏观应力在此应变区域仍然存在,其出现的先后顺序表明产生宏观应力所需的能量要低于微观应力,样品在受到力的作用时,宏观应力优先出现。这为宏观应力和微观应力的竞争现象提供了试验证据。
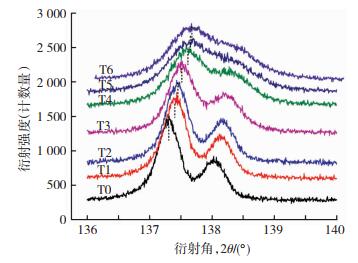
|
图 8 不同应变下(422)衍射峰 Fig.8 XRD peak of (422) under different strain |
由图 8数据可知,衍射峰位不断向高角度移动。从图 9可知,在弹性变形区,样品半高宽较为恒定,在塑性变形区,衍射峰半高宽持续增加。综合图 8、9的结果得出结论,在近断裂区样品晶粒内部宏观应力与微观应力同时存在。从图 2可以看出,数据点开始趋于平滑,此时缺少充足的钉扎中心Mg原子,PLC效应近乎结束。与随机取向晶粒相比,由于具有典型织构的晶粒数量较多,则其转动所需能量较大,这迫使随机晶粒方向向典型织构取向靠近,这是导致织构增加的主要原因。
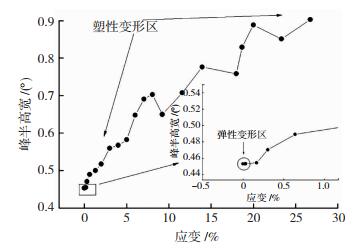
|
图 9 不同应变下(422)衍射峰半高宽 Fig.9 Half-width of XRD peak of (422) under different strain |
1) 在拉伸过程中,样品晶格应变、PLC效应、织构变化存在竞争规律并遵循能量最低原理。这一研究结果为塑性变形理论和实际应用提供了数据依据。
2) 晶格应变伴随整个拉伸过程:在弹性变形区,晶格常数线性减小;在塑性变形区,晶格常数减小趋势脱离线性,样品断裂后由于内部残余应力存在,晶格常数未恢复至初始状态。
3) 在拉伸过程中,样品内部首先产生宏观应力,该应力导致衍射峰向高角度漂移,但不改变衍射峰半高宽。其次产生微观应力,微观应力导致衍射峰半高宽增加,此时样品位错密度开始增加,宏观应力优先参与拉伸试验过程。
4) 在弹性变形区和初始塑性变形区,样品织构分布和占比未发生变化,随着PLC效应产生,由于衍射信号减弱,织构计算总量逐渐减小,在近断裂区,参与位错钉扎的Mg原子消耗殆尽,对晶粒的钉扎效应较弱,具有随机取向的晶粒开始向6种典型织构方向位置转动,织构总量和6种典型织构含量均呈现增加趋势。
5) 根据拉伸数据,从能量角度分析,试验涉及的微观效应所需能量从小到大依次为:晶格应变宏观应力、晶格应变微观应力、PLC效应、织构演化。
| [1] |
胡斌. 汽车行业发展对轻质结构部件的需求与展望[J]. 精密成形工程, 2020, 12(30): 121-124. HU Bin. Demand and prospect of light structural components for the development of automobile industry[J]. Journal of Netshape Forming Engineering, 2020, 12(30): 121-124. DOI:10.3969/j.issn.1674-6457.2020.03.014 |
| [2] |
王智文, 冯昌顺. 新能源汽车轻量化技术路径及开发策略[J]. 汽车工艺与材料, 2021, 6: 1-12. WANG Zhiwen, FENG Changshun. Light weight technology path and development strategy of new energy vehicles[J]. Automobile Technology & Material, 2021, 6: 1-12. DOI:10.19710/J.cnki.1003-8817.20210048 |
| [3] |
COTTRELL A H. A note on the Portevin-Le Chatelier effect[J]. Phil Mag, 1953, 44: 829-832. DOI:10.1080/14786440808520347 |
| [4] |
MCCORMICK P G. Theory of flow localization due to dynamic strain aging[J]. Acta Metallurgica, 1988, 36(12): 3061-3067. DOI:10.1016/0001-6160(88)90043-0 |
| [5] |
郝敏, 王亮, 陈军洲, 等. 2060-T8E30铝锂合金平面各向异性和断裂破坏机制研究[J]. 稀有金属, 2021, 45(6): 75-81. HAO Min, WANG Liang, LU Junzhou, et al. Study on plane anisotropy and fracture failure mechanism of 2060-T8E30Al-Li alloy[J]. Chinese Journal of Rare Metals, 2021, 45(6): 75-81. DOI:10.13373/j.cnki.cjrm.XY20120010 |
| [6] |
MARTON B, ADRIENN H, et al. Prediction of earing of aluminium sheets from {h00} pole figures[J]. European Journal of Mechanics-A/Solids, 2020, 81: 1-7. DOI:10.1016/j.euromechsol.2020.103950 |
| [7] |
王亮, 张泽东, 杜敏, 等. 铝合金汽车板罗平线的影响因素[J]. 理化检验-物理分册, 2020, 56(2): 21-24. WANG Liang, ZHANG Zedong, DU Min, et al. Influencing factors of roping line of aluminum alloy automobile sheets[J]. Physical Testing and Chemical Analysis PartA (PhysicalTesting), 2020, 56(2): 21-24. DOI:10.11973/lhjy-w1202002005 |
| [8] |
DUAN X G, JIANG H T, MI Z L, et al. Reduce the planar anisotropy of AA6016 Aluminum sheets by texture and microstructure control[J]. Crystal, 2020, 10: 1027-1042. DOI:10.3390/cryst10111027 |
| [9] |
王正安, 刘成, 罗兵辉, 等. 5A01高镁铝合金的PLC效应及其力学性能[J]. 材料科学与工程学报, 2010, 28(6): 813-817. WANG Zhengan, LIU Cheng, LUO Binghui, et al. Portevin-Le Chatelier effect and mechanical properties of 5A01 aluminum alloy[J]. Journal of Meterials Science and Engineering, 2010, 28(6): 813-817. DOI:10.14136/j.cnki.issn1673-2812.2010.06.019 |
| [10] |
彭开萍, 陈文哲, 钱匡武. 3004铝合金"反常"锯齿屈服现象的研究[J]. 物理学报, 2006, 55(7): 3569-3574. PENG Kaiping, CHEN Wenzhe, QIAN Kuangwu. Study of an anomalous serrated yielding phenomenon in 3004 aluminum alloy[J]. Acta Physica Sinica, 2006, 55(7): 3569-3574. DOI:10.7498/aps.55.3569 |
| [11] |
LEORA E, DRESSEIHAUS M, GRETHE W, et al. In situ visualization of long-range defect ineractions at the edge of melting[J]. Science Advances, 2021, 7: 1-8. DOI:10.1126/sciadv.abe8311 |
| [12] |
陈嘉亮, 彭开萍, 陈文哲. 3004铝合金中的PLC效应[J]. 材料导报, 2004, 18(8A): 237-239. CHEN Jialiang, PENG Kaiping, CHEN Wenzhe. The PLC effect of 3004 aluminum alloy[J]. Materials Reports, 2004, 18(8A): 237-239. |
| [13] |
HAN G M, TIAN C G, CHU Z K, et al. Activation energy calculations for the Portevin-Le Chatelier effect in nimonic 263 superalloy[J]. Metallurgical and Materials Transactions A, 2015, 46: 4629-4635. DOI:10.1007/s11661-015-3000-7 |
| [14] |
熊彪. 3003铝合金材料制耳率的控制[J]. 铝加工技术工程, 2020(1): 34-36. XIONG Biao. Control of earing rate of 3003 aluminum alloy material[J]. Aluminum Fabrication, 2020(1): 34-36. DOI:10.3969/j.issn.1005-4898.2020.01.08 |
| [15] |
SHI C, MAO X Q, SHEN K. Effect of annealing temperature on microstructure, texture and earing of 8011 cold rolled sheet[J]. Journal of Physics: Conference Series, 2021, 1802: 022045-022057. DOI:10.1088/1742-6596/1802/2/022045 |
| [16] |
刘伟, 吴远志, 邓彬, 等. 时效工艺对6061铝合金力学性能各向异性的影响及微观组织研究[J]. 材料导报, 2021, 35(4): 04134-04138. LIU Wei, WU Yuanzhi, DENG Bin, et al. Effect of aging processes on the anisotropic mechanical property of 6061 aluminum alloy and the related microstructure evolution[J]. Materials Reports, 2021, 35(4): 04134-04138. DOI:10.11896/cldb.19100070 |
| [17] |
段晓鸽, 江海涛, 米振莉, 等. 轧制方式对6016铝合金薄板组织和塑性各向异性的影响[J]. 材料工程, 2020, 48(8): 134-141. DUAN Xiaoge, JIANG Haitao, MI Zhenli, et al. Effect of rolling mode on microstructure and plastic anisotropy of 6016 aluminum alloy sheet[J]. Journal of Materials Engineering, 2020, 48(8): 134-141. DOI:10.11868/j.issn.1001-4381.2019.000766 |
| [18] |
PAWLIK K. Determination of the orientation distribution function from pole figures in arbitrarily defined cells[J]. Phys Stat Sol (B), 1986, 134: 477-483. DOI:10.1002/pssb.2221340205 |
| [19] |
RAABE D, LUCKE K. Investigation of the ADC method for Direct ODF approximation by means of standard functions[J]. Phys Stat Sol (B), 1953, 180: 59-65. DOI:10.1002/pssb.2221800103 |
| [20] |
RAABE D. Examination of the iterative series expansion method for quantitative texture analysis[J]. Texture and Microstructures, 1995, 23: 115-129. DOI:10.1155/TSM.23.115 |
| [21] |
张定铨, 何家文. 关于X射线衍射法测定微观应力的表征值的讨论[J]. 金属学报, 1998, 34(12): 1273-1278. ZHANG Dingquan, HE Jiawen. On characterization of microstress measured by X-ray diffraction[J]. Acta Metallurgica Sinica, 1998, 34(12): 1273-1278. |
| [22] |
ADACHI H, MIZOWAKI H, HIRATA M, et al. Measurement of dislocation density change during tensile deformation in coarse-grained aluminium by in-situ XRD technique with tester oscillation[J]. Materials Transaction, 2021, 62(1): 62-68. DOI:10.2320/matertrans.L-M2020861 |
 2022, Vol. 30
2022, Vol. 30


