纤维混凝土是将纤维作为增强相加入混凝土基体中的一种复合材料,纤维在基体中的分布状态、取向对混凝土性能提高起决定性作用。因此,轴向拉拔模型并不能完全反应复合材料开裂后纤维在开裂面上的桥接作用。在纤维的斜向拔出过程中,除了发生轴向模型中的脱黏以及滑移两种破坏过程外,还会发生纤维的弯曲、屈服和拉断[1],以及拔出点局部的基体屈服、破坏及剥落等现象。
目前对于纤维斜向拉拔模型研究分析的主要方向在于纤维掺量、纤维埋置深度、纤维与混凝土基体的黏结性能和机械咬合作用对于混凝土的增强作用。混凝土中单掺钢纤维体积分数在0%~2%时,钢纤维基体界面黏结性能随着钢纤维体积分数的增大而提升[2-3]。研究发现[4-6],相对于圆直型钢纤维,机械咬合作用使得异形钢纤维与混凝土形成的黏结性能更强。波纹型钢纤维在混杂纤维混凝土中的峰值拉拔力随着钢纤维埋置深度的增加而增大,但当埋置深度大于8 mm时,界面黏结强度随着埋置深度的增加而逐渐减小[7]。由于纤维在基体中的乱向分布,导致纤维斜向受拉,会使得纤维的桥接作用大幅度降低。由于混凝土基体自身的强度不同,纤维在混凝土基体中的桥接增强作用也不同。基于Tai等人[8]对钢纤维的静态和动态拔出的试验结果,在纤维取向从0°到45°,加载速率从0.018到1 800 mm/s,钩状和扭状钢纤维的最大拔出力均高于直状钢纤维。Yoo等人[9]研究结果表明,纤维倾角在45°时,半钩状钢纤维相比其他高度变形的钢纤维(如钩状和扭曲纤维)提供了更大的加载速率敏感性,平均黏结强度和拉拔能量。纤维倾斜角为30°和45°时,超高性能混凝土(UHPC)中所有直钢纤维和变形钢纤维均表现出最高的平均黏结强度,滑移能力随着倾角的增大而不断增加[10]。目前,对于纤维混凝土拉拔,大量学者认为在高强混凝土中,纤维对于混凝土的拉拔提升能力较为明显。Van等人[11]研究表明,要获得高性能纤维增强水泥复合材料的最大应变能力,应首选固定-固定边界条件。慕儒等人[12]研究表明,单向分布钢纤维增强水泥浆抗折强度显著提高。
现有研究中对于纤维拔出行为的描述大多建立于宏观力学层面,对于纤维拉伸试件破坏形态、纤维拔出过程中变形、脱黏机理及微观黏结性能研究相对较少,本文采用基体强度为110 MPa的超高性能混凝土(UHPC),选用3种类型(直线型、端勾型和波纹型)的钢纤维研究纤维在不同取向(0°、30°、45°和60°)下纤维拔出对于基体破坏形态、纤维变形及脱黏机理的影响。
1 实验 1.1 UHPC基体原材料及配合比UHPC基体的原材料包括:P·O 52.5普通硅酸盐水泥; I级粉煤灰; 硅灰; 采用普通河砂(比重2.6 g/cm3); 聚羧酸减水剂,减水率(质量分数)大于25%; 符合GJG-2006《混凝土用水标准》的混凝土拌和水。UHPC基体的配合比见表 1。
| 表 1 UHPC基体配合比 Table 1 Mix design of UHPC matrix |
试验采用平直型、端勾型和波纹型3种形状的钢纤维,纤维与拔出荷载轴线方向的夹角为0°、30°、45°、60°,钢纤维参数如表 2所示。
| 表 2 纤维参数及抗拉强度 Table 2 Fiber parameters and tensile strength |
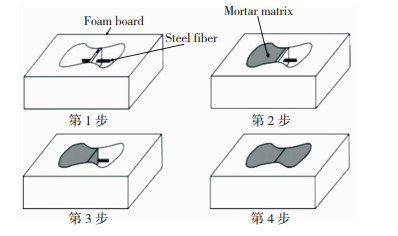
按表 1称取UHPC基体的原材料,将原材料(不包括水)置于搅拌锅中,干混90 s后将水倒入搅拌锅中,慢搅2 min,然后快搅3 min后停机出料,每组成型5个试件。所有纤维拔出试验样品均按照图 1所示制备:纤维用泡沫板固定在模具中心; 将水泥砂浆注入埋入端试模,养护24 h; 拆除泡沫板; 水泥砂浆注入另一半试模,养护24 h后拆模; 进行标准养护(温度(20±1) ℃,湿度(90±1)%)。图 2为纤维排列方式示意图。试验均采用了单纤维试样。
|
图 1 纤维拔出试件制备工艺 Fig.1 Fiber pull-out specimen preparation process |

|
图 2 纤维排列方式示意图 Fig.2 Schematic diagram of fiber arrangement |
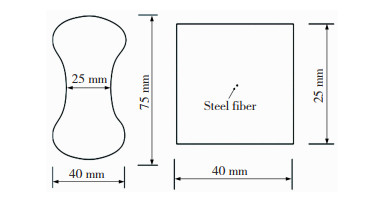
界面拉伸载荷通过最大容量为300 kN,加载速率为0.5 mm/min的万能拉伸试验机施加,混凝土试件尺寸如图 3所示,混凝土试件加载装置如图 4所示。
|
图 3 混凝土试件几何形状 Fig.3 Concrete specimen geometry |

|
图 4 加载装置示意图 Fig.4 Schematic diagram of loading device |
参照CECS13:2009《纤维混凝土试验方法标准》中钢纤维与水泥砂浆黏结强度实验方法,进行28 d界面拉伸实验。对试件进行连续、均匀加载,加载速率为0.5 mm/min,同时启动自动记录装置,当出现最大荷载或钢纤维滑移量超过2.5 mm时,停止试验。
纤维-基体的平均粘结强度按式(1)计算
| $ f_{\mathrm{b}}=\frac{F_{\max }}{n \mu_{\mathrm{f}} L_{\mathrm{em}}} $ | (1) |
式中:fb为纤维基体粘结强度,MPa; Fmax为最大拉拔载荷,N; n为试验纤维根数; μf为纤维横截面周长; Lem为纤维拔出长度。
纤维-基体拔出能按式(2)计算
| $ W_{\mathrm{e}}=\int_{s=0}^{s=L_{\mathrm{e m}}} P(s) \mathrm{d} s $ | (2) |
式中:We纤维拔出能,J; P(s)为纤维拉拔曲线。
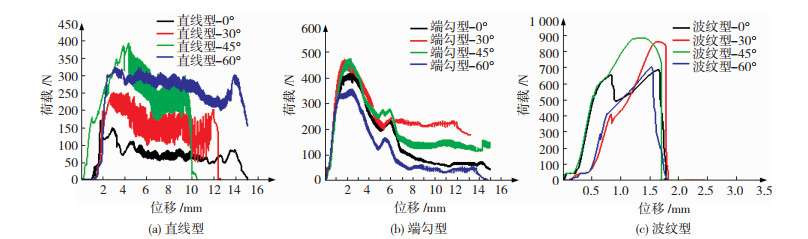
2 结果与讨论 2.1 拉伸性能 2.1.1 纤维取向及类型对纤维-UHPC基体界面黏结性能的影响不同类型纤维和取向下纤维拔出荷载-位移曲线如图 5所示。由图 5(a)可以看出,随着取向角的增加,直线型钢纤维拔出荷载分别为189.574、252.102、394.566、324.549 N。当取向为45°时达到最大值为394.566 N,原因是直线型纤维表面比较光滑,当纤维取向夹角较小时纤维在拔出过程中主要表现出脱黏和滑移两种破坏,随着纤维取向角的增大,会发生纤维的弯曲、屈服、拉断,以及拔出点局部的基体屈服、破坏及剥落等现象。由图 5(b)可以看出,随着纤维取向的增加,端勾型钢纤维拔出荷载分别为425.370、472.734、476.634和355.634 N,当取向为45°时拔出荷载达到最大值476.634 N,端勾型纤维拔出荷载大于直线型荷载的主要原因在于,端勾型钢纤维由于尾部端勾部分增加了纤维与基体之间的机械咬合作用。由图 5(c)可以看出随着纤维取向的增加,波纹型钢纤维的拔出荷载分别为687.195、861.123、886.974和784.722 N,当纤维取向为45°时达到最大值886.974 N,波纹型钢纤维拔出荷载大于直线型和端勾型钢纤维的主要原因是,波纹型钢纤维由于其表面波纹的存在增加了基体和纤维的接触面积及基体与纤维的咬合部分,从而使得波纹型钢纤维拔出荷载最大。
|
图 5 不同纤维类型及取向界面的拉伸荷载-位移曲线 Fig.5 Tensile load-displacement curves for different fiber types and orientation interfaces: (a) linear type; (b) end-hook type; (c) corrugated type |
不同类型的纤维随着纤维角度的变化,其拔出荷载、平均黏结强度、界面能变化的具体结果如表 3所示。由表 3可知,直线型钢纤维拔出荷载在45°时达到最大值394.566 N,在0°时为189.574 N,提高了108.133%; 界面能在纤维取向为60°时达到最大值为3 558.297 N·mm,在纤维取向为0°时其值为1 070.317 N·mm,提高了232.453%; 平均黏结强度在取向为45°时达到最大值为10.466 MPa,在纤维取向为0°时为5.029 MPa,提高了108.13%。
| 表 3 不同类型及取向纤维拔出性能参数试验结果 Table 3 Test results of pull-out performance parameters of fibers with different types and orientations |
端勾型钢纤维拔出荷载在纤维取向为45°时达到最大值476.634 N,在0°时为425.370 N,提高了12.05%; 界面能在纤维取向为30°时达到最大值为3 429.828 N·mm,在纤维取向为0°时为2 408.290 N·mm,提高了42.418%; 平均黏结强度在纤维取向为45°时达到最大值为11.559 MPa, 在纤维取向为0°时为10.316 MPa,提高了12.05%。
波纹型钢纤维拔出荷载在纤维取向为45°时达到最大值886.974 N,在0°时为687.195 N,提高了29.07%; 界面能在纤维取向为45°时达到最大值为1 007.108 N·mm,在0°时为798.359 N·mm,提高了26.222%; 平均黏结强度在取向为45°时达到最大值为84.473 MPa, 在取向0°时为65.447 MPa,提高了29.07%。
可见,3种类型纤维拔出荷载和平均界面黏结强度都是先增大后减小,在纤维取向为45°时达到最大值,直线型钢纤维随着纤维取向的增大拔出能逐渐增大,端勾型钢纤维拔出能先增大后减小,波纹型钢纤维由于拔出时纤维产生脆性断裂,导致拔出能相对较小。这也论证了纤维增强高性能混凝土中异形纤维相对于直线型纤维对于强度性能提升更加明显。
2.1.3 纤维取向和类型对UHPC破坏形态影响如图 6所示,由于拔出荷载增加,倾斜钢纤维在完全从基体中拔出之前与基体脱黏。从图中可以看出,大角度倾斜钢纤维造成的基体剥落面积明显大于小角度倾斜时的基体剥落面积[13]。波纹型钢纤维由于较大的黏结强度和持续激活的机械锚固效应而发生严重的基体剥落,对周围基体造成更大的损伤。相反,波纹型钢纤维黏结滑移位移在1~2 mm,远远小于纤维长度的一半。虽然倾斜的波纹型钢纤维在达到实际黏结强度之前过早断裂,但其表现出最高的平均黏结强度,在所有取向下从43.596 MPa到84.473 MPa。与直线型和端勾型钢纤维相比,波纹型的钢纤维峰后黏结应力随着滑移降低更快。然而,随着取向的增加,波纹型钢纤维的平均黏结强度变化规律与直线型和端勾型钢纤维相同,都是在45°时达到最大值[14]。由图 6可以看出3种类型钢纤维试件在纤维取向为60°时,基体破坏程度逐渐增大,这是由于纤维在基体内过度锚固,导致基体过早破坏,从而使得平均黏结强度有所降低。

|
图 6 纤维拔出后基体与破坏面形貌图:(a)~(c)直线型0°、45°、60°; (d)~(f)端钩型0°、45°、60°; (g)~(i)波纹线0°、45°、60° Fig.6 Shapes of matrix and damage surfaces after fiber pull-out: (a)~(c) linear type at 0°, 45°, 60°; (d)~(f) end-hook type at 0°, 45°, 60°; (g)~(i) corrugated type at 0°, 45°, 60° |
不同纤维取向、类型下的钢纤维荷载-位移曲线第一峰值结果如表 4所示。由表 4可知,直线型钢纤维随着纤维取向的增加,荷载-位移曲线第一峰值分别为41.340、198.159、179.877和268.881 N; 端勾型钢纤维随着纤维取向的增加,荷载-位移曲线第一峰值分别为44.040、82.905、168.111和209.097 N; 波纹型钢纤维随着纤维取向的增加荷载-位移曲线第一峰值变化不大,分别为42.289、39.846、46.598和42.569 N。可见,对于直线型钢纤维,随着纤维取向逐渐增加,第一峰值荷载先增大后减小,当纤维取向为30°时,第一峰值荷载提高较大,这是由于对于斜向拔出荷载来说水平位移的产生只是斜向拔出荷载的一个分力。对于端勾型钢纤维,随着纤维取向的增加,荷载-位移曲线第一峰值逐渐增加,这是由于随着纤维取向增加,角度摩擦以及弯矩的附加摩擦作用增强,初始纤维和基体脱黏逐渐困难。在波纹型型钢纤维中,随着纤维取向的增加,荷载-位移曲线第一峰值基本保持不变,这是由于波纹型钢纤维由于纤维本身形状作用,导致纤维与基体的机械咬合容易松动,更容易产生脱黏。
| 表 4 不同类型及取向纤维拔出荷载-位移曲线第一峰值 Table 4 First peak of load-displacement curves for fiber pull-out with different types and orientations |
对于端勾型钢纤维,最大拔出荷载对应的位移约为2 mm,近似和端勾纤维弯钩端长度相似,随后位移中最高峰逐渐降低,这充分说明,端勾型钢纤维的拉拔阻抗来自于尾部弯钩的拉直作用,钢纤维初始形态对拉拔结果有重要影响。
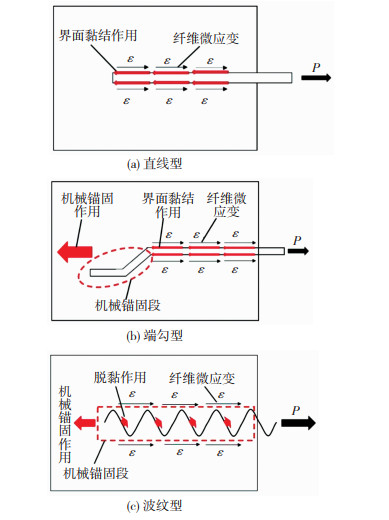
2.3 纤维拔出过程中脱黏机理分析图 7给出了不同类型纤维的脱黏机理。由图 7(a)可知,直线型钢纤维在拔出过程中,由于外部荷载作用,导致纤维会产生向外滑移的趋势。在基体内纤维与混凝土基体产生界面黏结作用,导致纤维在受拉时会产生微变形,由于直线型钢纤维形状,在受拉时单位滑移承受微应变作用较小,当外部荷载大于整段纤维黏结作用时,纤维脱黏,从基体中被拔出[15]。随着纤维取向的增加,由于黏结作用对拔出能力逐渐增强,导致荷载-位移曲线第一峰值荷载逐渐增大。
|
图 7 不同类型纤维脱黏机理 Fig.7 Debonding mechanism of different types of fibers: (a) linear type; (b) end-hook type; (c) corrugated type |
由图 7(b)可知,端勾型钢纤维拔出过程中,在初始拉伸时,直线段部分和直线型钢纤维受力情况一致,由于端勾部位的存在,端勾部位会产生较小的机械锚固作用,导致初始脱黏时端勾型钢纤维初始脱黏荷载大于直线型钢纤维。
由图 7(c)可知,波纹型钢纤维在拔出过程中,由于纤维自身比表面积较大,导致纤维与基体黏结作用较强,因此由于黏结作用造成的第一峰值荷载最大。当纤维取向逐渐增加,由于黏结作用相对机械锚固作用较小,当外部荷载逐渐增大,纤维会产生斜向的脱黏作用,导致波纹型钢纤维在达到初始脱黏荷载之后,完全由机械锚固承受外部荷载,直到纤维被拔出或拉断。
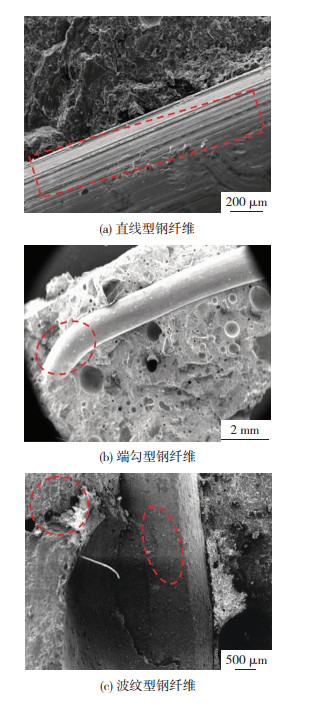
2.4 纤维-UHPC基体黏结作用微观分析图 8给出了不同类型纤维-UHPC基体的黏结微观形貌。由图 8(a)可以看出,纤维表面由于滑移导致纤维表面产生较多划痕,因此纤维在拔出过程中荷载-位移曲线会抖动,由于纤维尺寸较为均一,在拔出时对混凝土基体破坏较小,因此纤维附近混凝土整体性较好。由图 8(b)可以看出,端勾型钢纤维由于机械锚固作用,纤维与基体黏结性能较好。由图 8(c)可以看出,波纹型钢纤维由于波纹存在拔出时对纤维附近基体造成破坏,纤维表面划痕较少,这是由于纤维滑移距离较短。波纹型钢纤维在拔出过程中,由于纤维自身比表面积较大,所以纤维与基体机械锚固作用较强,但也因为波纹的存在,导致拉伸时纤维两侧基体产生破坏。
|
图 8 不同类型纤维-UHPC基体黏结微观图 Fig.8 Microscopic view of bonding of different types of fiber-UHPC matrix: (a) linear steel fiber; (b) end-hook type steel fiber; (c) corrugated steel fiber |
1) 直线型、端勾型和波纹型钢纤维在拔出过程中由于纤维形状原因导致波纹型钢纤维拔出荷载最大,端勾型钢纤维次之,直线型钢纤维最小,3种纤维都在纤维取向为45°时拔出荷载达到最大值。由于纤维形状的原因,波纹型钢纤维在拔出时会有明显的纤维拉断现象。
2) 从荷载-位移曲线第一峰值可知,波纹型钢纤维相比于直线型和端勾型钢纤维更容易脱黏。斜向拔出时基体更容易产生较大的应力集中,从而导致基体表面产生破坏。
3) 从受力行为分析,直线型钢纤维在拔出过程中首先发生纤维与基体的脱黏,随后纤维被拔出。而端勾型钢纤维和波纹型钢纤维在拔出过程中需最先克服界黏结及机械锚固作用,随后纤维产生变形直至完全拔出。
| [1] |
ROY M, HOLLMANN C, WILLE K. Influence of fiber volume fraction and fiber orientation on the uniaxial tensile behavior of rebar-reinforced ultra-high performance concrete[J]. Fibers, 2019, 7(7): 67. DOI:10.3390/fib7070067 |
| [2] |
程俊, 刘加平, 张丽辉. 超高性能混凝土纤维基体黏结性能测试与机理分析[J]. 混凝土与水泥制品, 2016(5): 62-66. CHEN Jun, LIU Jiaping, ZHANG Lihui. Testing and mechanism analysis of the fiber-matrix bonding properties of ultra-high performance concrete[J]. China Concrete and Cement Products, 2016(5): 62-66. DOI:10.19761/j.1000-4637.2016.05.014 |
| [3] |
DENG F Q, DING X X, CHI Y, et al. The pull-out behavior of straight and hooked-end steel fiber from hybrid fiber rein-forcedcementitious composite: experimental study and analytic modeling[J]. Composite Structures, 2018, 206: 693-712. DOI:10.1016/j.compstruct.2018.08.066 |
| [4] |
BANTHIA N, TROTTIER J F. Micromechanics of steel fiber pull-out: rate sensitivity at very low temperatures[J]. Cement & Concrete Composites, 1992, 14(2): 119-130. DOI:10.1016/0958-9465(92)90005-G |
| [5] |
MUSTAFA K I, EKHLAS A A, SAFAA M H, et al. Shear strength of steel fiber/polyepoxide resin interface using single fiber pull-out tests[J]. Reinforced Plastics, 2020, 64(2): 103-108. DOI:10.1016/j.repl.2019.07.004 |
| [6] |
SUMITRO S, TSUBAKI T. Micromechanical fiber pullout model for steel fiber reinforced concrete[J]. Doboku Gakkai Ronbunshu, 2010(599): 155-163. DOI:10.2208/jscej.1998.599_155 |
| [7] |
王力, 徐礼华, 邓方茜, 等. 波纹型钢纤维混杂纤维混凝土界面黏结性能[J]. 建筑材料学报, 2020(4): 865-874. WANG Li, XU Lihua, DENG Fangqian, et al. Interfacial bonding performance between corrugated steel fiber and hybrid fiber concrete matrix[J]. Journal of Building Materials, 2020(4): 865-874. DOI:10.3969/j.issn.1007-9629.2020.04.019 |
| [8] |
TAI Y S, EL-TAWIL S. High loading-rate pullout behavior of inclined deformed steel fibers embedded in ultra-high-performance concrete[J]. Construction & Building Materials, 2017, 148(1): 204-218. DOI:10.1016/j.conbuildmat.2017.05.018 |
| [9] |
YOO D Y, KIM S. Comparative pullout behavior of half-hooked and commercial steel fibers embedded in UHPC under static and impact loads[J]. Cement and Concrete Composites, 2019, 97: 89-106. DOI:10.1016/j.cemconcomp.2018.12.023 |
| [10] |
YOO D Y, KIM S, KIM J, et al. An experimental study on pullout and tensile behavior of ultra-high-performance concrete reinforced with various steel fibers[J]. Construction and Building Materials, 2019, 206: 46-61. DOI:10.1016/j.conbuildmat.2019.02.058 |
| [11] |
VAN ZIJL G P A G, SLOWIK V, TOLEDO FILHORD R D, et al. Comparative testing of crack formation in strain-hardening cement-basedcomposites (SHCC)[J]. Materials & Structures, 2016, 49(4): 1175-1189. DOI:10.1617/s11527-015-0567-9 |
| [12] |
慕儒, 李辉, 王晓伟, 等. 单向分布钢纤维增强水泥基复合材料(Ⅱ): 制备及钢纤维增强作用[J]. 建筑材料学报, 2015, 18(3): 387-392. MU Ru, LI Hui, WANG Xiaowei, et al. Aligned steel fiber reinforced cement based compo-sites(Ⅱ): preparation and reinforcement of aligned steel fibers[J]. Journal of Building Materials, 2015, 18(3): 387-392. |
| [13] |
YOO D Y, KANG S T, LEE J H, et al. Effect of shrinkage reducing admixture on tensile and flexural behaviors of UHPFRC considering fiber distribution characteristics[J]. Cement & Concrete Research, 2013, 54: 180-190. DOI:10.1016/j.cemconres.2013.09.006 |
| [14] |
WILLE K, NAAMAN A E, EL-TAWIL S, et al. Ultra-high performance concrete and fiber reinforced concrete: achieving strength and ductility without heat curing[J]. Materials & Structures, 2012, 45(3): 309-324. DOI:10.1617/s11527-011-9767-0 |
| [15] |
刘浩洋, 吕超雨, 石姗姗, 等. 芳纶纤维增韧碳纤维增强环氧树脂复合材料-铝蜂窝夹芯结构界面性能和增韧机制[J]. 复合材料学报, 2022, 39(2): 567-575. LIU Haoyang, LV Chaoyu, SHI Shanshan. Interfacial properties and toughening mechanism of aramid fiber toughened carbon fiber reinforced epoxy resin composite-aluminum honeycomb sandwich structure[J]. Acta Materiae Compositae Sinica, 2022, 39(2): 567-575. DOI:10.13801/j.cnki.fhclxb.20210526.002 |
 2022, Vol. 30
2022, Vol. 30


