2. 内蒙古自治区先进制造技术重点实验室, 呼和浩特 010051
2. Inner Mongolia Key Laboratory of Advanced Manufacturing Technology, Hohhot 010051, China
TC4钛合金由于其出色的力学性能,在航空航天、汽车等领域得到了广泛的应用。由于其本身的密度较小约为钢的一半,但其强度却远高于钢,因此受到各行各业的青睐[1-2]。采用钛合金可以制造出高强度但质量轻的零部件,这恰恰是航空、汽车领域所追求的[3-4]。近年来,随着TC4钛合金的广泛使用,人们对材料的力学性能要求越来越高,对其疲劳特性的研究也越来越深入[5-6]。刘行等人[7]基于超高周渗碳钢疲劳试验,通过两参数泊松分构建了虑及最大应力的竞争失效模型,表明了试样表面失效以及内部失效之间的竞争关系; Liu等人[8]通过泊松分布计算试样致命缺陷的发生概率,建立了表面及内部失效的竞争失效模型,但其模型未考虑尺寸小于50 μm的缺陷特征; Hu等人[9]通过量化冲击载荷对系统可靠性进行分析,且提出系统竞争失效的可靠度模型。丁力等人[10]通过逆高斯过程建模以及威布尔分布建模,通过实验数据对比,得出逆高斯过程的竞争失效模型预测结果较好,但其仅考虑了冲击载荷并未考虑其它因素。综上所述,能够综合考虑试样施加应力大小、缺陷尺寸以及失效模式的模型还未有人构建。因此,本文在虑及上述因素的基础上,构建TC4竞争失效模型。由于最大应力强度因子对于表征试样解理、失效等具有重大意义[11],其强相关于最大应力,裂纹尺寸以及失效模式,因此,基于最大应力强度因子构建的竞争失效模型有较强的科学性、针对性。
本文在两种应力比下,开展TC4钛合金超高周疲劳试验,研究其各种失效模式,并探明失效模式之间的竞争关系。建立基于最大应力强度因子的TC4竞争失效模型,用于表征不同的最大应力强度因子值下各种模式的失效概率。为人们对钛合金竞争失效模式的评估提供新的方法,该结果对钛合金的安全服役评估有很大的帮助。
1 实验 1.1 材料及试样材料选择TC4钛合金, 其化学成分(质量分数) 为: 6.29%Al、4.14%V、0.029% Fe、0.023% C、0.19% O、0.006 8% N、0.004 4% H。将试样加工成沙漏型,然后用360目数至2 000目数的砂纸打磨试样圆弧区域直至其光滑且无肉眼可见缺陷,并测得试样最终尺寸如图 1所示。
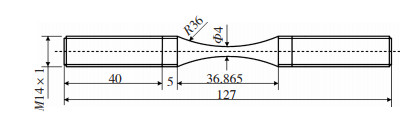
|
图 1 疲劳测试试样(单位:mm) Fig.1 Fatigue test specimen |
采用体积含量4%的乙醇硝酸腐蚀液对超高周疲劳试验得到的试样进行处理,利用LEICA DM4000M光学显微镜以及JSM-6610LV扫描电子显微镜(SEM)观察TC4钛合金微观组织; 采用MTS 809材料测试系统对TC4钛合金的力学性能进行测量; 采用Nano-Indenter-G200纳米压痕硬度测量仪测量材料的微观硬度。在打磨-抛光后的试样截面上,以100 μm为间隔从截面边缘至心部沿直径取20个试验点进行测量,测得硬度值后通过换算关系1 GPa = 102.04HV转化为维氏硬度值。采用高频疲劳试验机,针对TC4钛合金开展超高周疲劳试验,加载频率约为95 Hz,执行的应力比分别为-1、-0.3。
2 结果与讨论 2.1 微观组织和力学性能TC4钛合金微观组织如图 2所示。测得TC4钛合金的晶体大致分为两种,分别为αp与αs+β晶体。其中αp晶体表面较光滑、大致呈椭圆形,占据试样大部分体积; αs+β晶体表面较粗糙、形状不规则。

|
图 2 微观组织特征 Fig.2 Microstructure characteristics: (a) optical microscope; (b) scanning electron microscope |
力学性能测试表明,TC4钛合金的弹性模量为111 GPa、抗拉强度为1 033 MPa、屈服强度为980 MPa、断面收缩率为46.2%、延长率为17.2%。TC4钛合金的硬度分布如图 3所示。可见,硬度保持一个恒定值,平均维氏硬度为319HV。
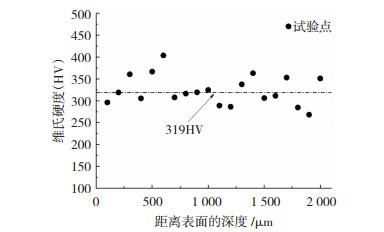
|
图 3 维氏硬度分布 Fig.3 Vickers hardness distribution |
基于TC4钛合金在室温及两种应力比下(R分别为-1、-0.3)的超高周疲劳试验结果,绘制疲劳S-N曲线如图 4所示。由图 4可见,两种应力比下,TC4钛合金表现出了不同的失效形式,当R=-0.3时,试样有表面(Sur)以及内部(Int)两种失效模式,整体呈现出“双线性”S-N特性[12],“小平台”表明其存在传统疲劳极限,约为815 MPa; 当R=-1时,所有试验点的破坏形式均为表面疲劳失效,其“小平台”代表传统疲劳极限,约为620 MPa。
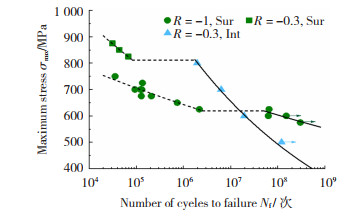
|
图 4 两种应力比下的疲劳S-N曲线 Fig.4 Fatigue S-N curves under two stress ratios |
通过SEM对TC4钛合金疲劳试样断口形貌的观察,可发现在应力比为-1、-0.3下,TC4钛合金有两种失效模式,这也与疲劳S-N曲线的分析结果一致。
1) 表面失效:由图 5(a)可以清晰看到表面裂纹源,在循环应力作用下,试样的表面缺陷(Surface Defect,SD)诱发裂纹,表面缺陷通常是由于试样机械加工而造成的缺陷,其表现为试样表面存在凹坑。裂纹由此处萌生并向内部生长,最终试样断裂。由图 5(b)可知,表面缺陷可近似为半椭圆形,将aSD定义为表面缺陷深度。且其附近观察到有解理刻面产生,解理刻面的形成是正应力作用下金属的原子键遭到破坏而导致晶体产生的一种穿晶断裂,其面积约等于晶粒横截面积。因此可以认为解理刻面为圆形,将rfacet定义为解理刻面半径。
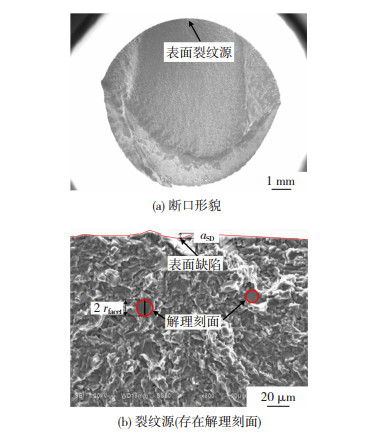
|
图 5 表面失效试样断口图(R=-0.3, σmax=825 MPa, Nf = 43 900) Fig.5 Fracture diagram of specimen with surface failure: (a) fracture morphology; (b) crack source (with cleavage facet) |
2) 内部失效:由图 6(a)可知,试样初始裂纹由内部产生,且并无其它裂纹源,因此定义其为内部失效。由图 6(b)可知,断口组织存在内部粗糙不均匀区,该域由大量解理刻面组成(图 6(c)),由于该区域内晶界分布不均匀,造成其硬度分布不均匀,使得晶界处易产生应力集中[13],进而微裂纹易在该处萌生,并最终导致式样断裂。
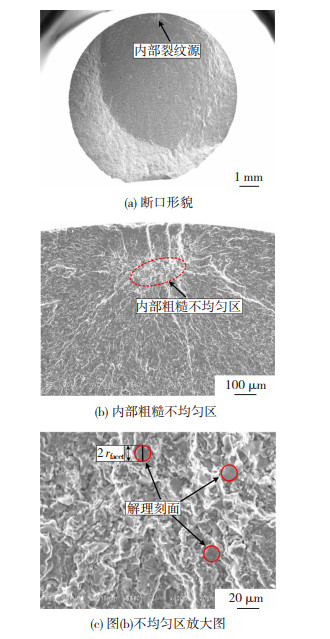
|
图 6 内部失效(有解理刻面)试样断口图(R=-0.3, σmax=600 MPa, Nf = 1.94291e7) Fig.6 Fracture diagram of specimen with internal failure (cleavage facet): (a) fracture morphology; (b) internal rough and uneven area; (c) enlarged view of uneven area of Fig. 6 (b) |
利用ImageJ图形测量软件对试样断口的表面缺陷深度、内部解理刻面特征尺寸进行测量,得到TC4钛合金在两种应力比下的特征尺寸值与疲劳寿命之间的关系, 如图 7所示。内部起裂试样的解理刻面半径范围为4.4~5.1 μm。可以得出,随着寿命的增加及应力比的增大,解理刻面半径大小不发生变化,均值为4.67 μm。同时,在R=-1时,试样失效模式均为表面失效,aSD均值为5.45 μm; 在R=-0.3时,试样有两种失效模式:表面失效、以及内部失效。通过试样两种应力比的缺陷尺寸分布得出:试样初始缺陷仅与试样加工工艺和内部晶粒尺寸大小有关。
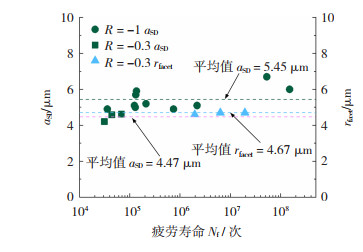
|
图 7 aSD、rfacet与疲劳寿命Nf的关系图 Fig.7 Relationship between aSD, rfacet, and fatigue life Nf |
应力强度因子是表征裂纹失效模式的重要参数。其内部解理刻面rfacet对应的最大应力强度因子Kint-max的表达式为[14]
| $ K_{\text {int-max }}=\frac{2}{\pi} \sigma_{\max } \sqrt{\pi r_{\text {facet }}} $ | (1) |
表面缺陷aSD对应的最大应力强度因子Ksur-max表达式为[15]
| $K_{\text {sur-max }}=\frac{1.12 \sigma_{\max } \sqrt{\pi a_{\mathrm{SD}}}}{E(k)} \approx \sigma_{\max } \sqrt{\pi a_{\mathrm{SD}}} $ | (2) |
式中E(k)为一个介于1和π/2之间的数,故1.12/E(k) ≈ 1。因此,得出最大应力强度因子值Kmax与疲劳寿命Nf之间的关系,如图 8所示。
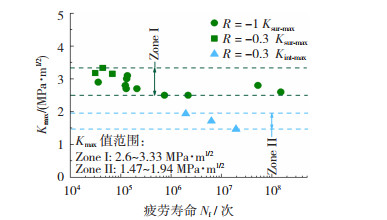
|
图 8 Kmax与Nf的关系图 Fig.8 Relationship between Kmax and Nf |
由图 8可知,在两种应力比下,表面失效Ksur-max的范围Zone I为2.6~3.33 MPa·m1/2,随着寿命增加,Ksur-max值无明显变化; 在R=-0.3下,内部失效的Kint-max范围Zone II为1.47~1.94 MPa·m1/2,且随着寿命增加,Kint-max有减小的趋势。通常,疲劳试样的寿命强相关于疲劳试样的失效模式、最大应力以及缺陷尺寸。由于Kmax值与失效模式、最大应力以及缺陷尺寸均密切相关,因此可以利用Kmax构建TC4多元竞争失效模型。
3 竞争失效模型由上文可知,本文所研究的TC4钛合金有两种疲劳失效模式。有研究指出,材料所受到的最大应力强度因子是晶体发生解理断裂行为的重要因素,当最大应力强度因子达到晶粒发生解理断裂的阈值时,晶粒便发生解理,试样断口表面会观察到光滑的刻面; 若达不到阈值,初始裂纹由试样表面或内部萌生、扩展直至试样断裂,在此过程中不会产生解理刻面。基于此,以最大应力强度因子为主要因素构建表征钛合金疲劳失效模式转变的竞争失效模型。
基于最大应力强度因子,试样内部晶粒发生解理断裂的概率服从正态分布[16]
| $ f\left(K_{\max }\right)=\frac{1}{\sqrt{2 \pi} \rho} e^{-\frac{K_{\max }-K_{c, \mathrm{~m}}}{2 \rho^{2}}} $ | (3) |
式中:Kmax为最大应力强度因子; Kc, m为最大应力强度因子的平均值; ρ为最大应力强度因子的标准差。
对式(3)概率密度函数进行积分运算,得到累计概率分布函数F(Κmax)。因此,基于两参数泊松分布,计算出晶粒有概率解理断裂的个数为
| $ N=F \frac{A}{\alpha} $ | (4) |
式中:A为试样横截面面积; a为单个晶粒截面面积。
因此,横截面内晶粒解理断裂的概率为
| $ P(n)=e^{-N} \frac{N^{n}}{n !} $ | (5) |
由式(5)可知,当n = 0时,表示试样不发生解理断裂; 当n ≥ 1时,表示试样发生解理断裂,其概率分别为:
| $ P(n=0)=e^{-N} $ | (6) |
| $ P(n \geqslant 1)=1-e^{-N} $ | (7) |
定义试样发生内部疲劳失效的面积为Aint、试样发生表面疲劳失效的面积为Asur。因此,发生在Aint及Asur内解理断裂的晶粒数目为:
| $ \begin{aligned} N_{\mathrm{int}}=F A_{\mathrm{int}} / a \end{aligned} $ | (8) |
| $ N_{\mathrm{sur}}=F A_{\mathrm{sur}} / a $ | (9) |
由于试样不可避免的存在着表面缺陷,相较于内部失效,试样更易发生表面失效,也就是说表面失效会优先于内部失效发生。概率为
| $ P_{\mathrm{II}}=P_{\mathrm{sur}}(n \geqslant 1)=1-e^{-N_{\mathrm{sur}}} $ | (10) |
当试样表面的晶粒不能够发生解理断裂,疲劳裂纹则会由Aint内部萌生。因此内部失效发生的概率为
| $ P_{\mathrm{III}}=P_{\mathrm{sur}}(n=0) P_{\mathrm{int}}(n \geqslant 1)=\left(1-e^{-N_{\mathrm{int}}}\right) e^{-N_{\mathrm{sur}}} $ | (11) |
当试样没有任何晶粒能够发生解理断裂时,其发生失效的概率为
| $P_{\mathrm{I}}=P_{\mathrm{sur}}(n=0) P_{\mathrm{int}}(n=0)=e^{-N_{\mathrm{sur}}} e^{-N_{\mathrm{int}}} $ | (12) |
图 9给出了失效概率与应力强度因子之间的关系。由图 9知,本模型预测结果区间定义为当失效概率达到1%和99%时,将此概率下的最大应力强度因子定义为区间端点。因此,无缺陷试样发生失效的Ksur-max范围为0~2.05 MPa·m1/2,表面失效试样Ksur-max范围为>1.64 MPa ·m1/2,内部失效的Kint-max范围为1.45~2.3 MPa·m1/2。与图 8对照得知,本模型预测结果较好,试验结果均被预测结果包含在内。
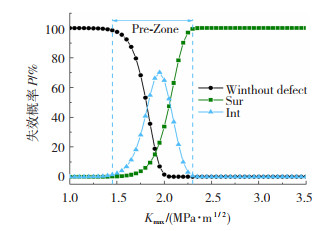
|
图 9 失效概率与应力强度因子的关系 Fig.9 Relationship between failure probability and stress intensity factor |
初始缺陷的形式和尺寸大小决定了应力强度因子,然后应力强度因子决定其对应的失效形式,亦即基于最大应力强度因子可得到该试验件的各种失效形式的失效概率。由图 9绘制的曲线趋势可以得出,当应力强度因子较低时,表面失效极易发生; 当应力强度因子增大时,无缺陷试样失效概率逐渐减小至0%,表面失效概率逐渐增大至100%,内部失效概率先增大后减小至0%。
4 结论1) 由疲劳试验结果可知,应力比-1、-0.3下的S-N曲线均呈现出双线性; 基于SEM观察得知,TC4钛合金有两种疲劳失效模式,即表面失效和内部失效。
2) Kmax值与失效模式、最大应力以及缺陷尺寸均密切相关,在两种应力比下,随着寿命增加,Ksur-max值无明显变化; 在R=-0.3下,随着寿命增加,Kint-max有减小的趋势。
3) 建立试样缺陷尺寸和最大应力与试样失效模式之间的关系,即最大应力强度因子与失效模式的关系,继而构建TC4竞争失效模型,可得出任一最大应力强度因子值下,试样发生各种失效模式的概率,为人们后续对TC4失效模式的研究提出新的且可靠的方法。
| [1] |
江琛琛, 高秋志, 甄云乾, 等. 热处理工艺对AFA耐热钢组织和力学性能的影响[J]. 材料科学与工艺, 2021, 29(2): 27-35. JIANG Chenchen, GAO Qiuzhi, ZHEN Yunqian, et al. Effect of heat treatment process on microstructure and mechanical properties of AFA heat-resistant steel[J]. Materials Science and Technology, 2021, 29(2): 27-35. DOI:10.11951/j.issn.1005-0299.20190146 |
| [2] |
曹守启, 何鑫, 刘婉荣, 等. Ti75合金激光焊接接头的组织及力学性能[J]. 材料科学与工艺, 2021, 29(1): 53-58. CAO Shouqi, HE Xin, LIU Wanrong, et al. Microstructure and mechanical properties of laser welded Ti75 alloy joint[J]. Materials Science and Technology, 2021, 29(1): 53-58. DOI:10.11951/j.issn.1005-0299.20200106 |
| [3] |
WANG Haibo, ZHAI Dajun, FENG Keqin. Effect of the microstructure of a titanium alloy fabricated using selective laser melting on microarc oxidation film[J]. Metallurgical and Materials Transactions, 2021, 52(10): 4691-4702. DOI:10.1007/S11661-021-06421-3 |
| [4] |
LIN Zidong, SONG Kaijie, YU Xinghua. A review on wire and arc additive manufacturing of titanium alloy[J]. Journal of Manufacturing Processes, 2021, 70: 24-45. DOI:10.1016/J.JMAPRO.2021.08.018 |
| [5] |
王存宇, 杨洁, 常颖, 等. 先进高强度汽车钢的发展趋势与挑战[J]. 钢铁, 2019, 54(2): 1-13. WANG Cunyu, YANG Jie, CHANG ying, et al. Development trend and challenge of advanced high strength automobile steels[J]. Iron and Steel, 2019, 54(2): 1-13. DOI:10.13228/j.boyuan.issn0449-749x.20180284 |
| [6] |
马世辉, 李积元. 轴肩直径对Ti-6Al-4V钛合金搅拌摩擦焊接头组织和性能的影响[J]. 钢铁钒钛, 2021, 42(3): 82-87. MA Shihui, LI Jiyuan. Influence of shaft shoulder diameter on microstructure and properties of Ti-6Al-4V friction stir welding joint[J]. Iron steel vanadium titanium, 2021, 42(3): 82-87. DOI:10.7513/j.issn.1004-7638.2021.03.012 |
| [7] |
刘行, 刘其晨, 于欢, 等. 不同应力比下渗碳齿轮钢多重竞争疲劳失效模型构建[J]. 内蒙古工业大学学报(自然科学版), 2019, 38(4): 282-291. LIU Hang, LIU Qichen, YU Huan, et al. Construction of multiple competing fatigue failure model for carburized gear steel with different stress ratio[J]. Journal of Inner Mongolia University of Technology (Natural Science Edition), 2019, 38(4): 282-291. DOI:10.13785/j.cnki.nmggydxxbzrkxb.20190817.009 |
| [8] |
LIU Fulin, HE Chao, CHEN Yao, et al. Effects of defects on tensile and fatigue behaviors of selective laser melted titanium alloy in very high cycle regime[J]. International Journal of Fatigue, 2020, 140: 105795. DOI:10.1016/j.ijfatigue.2020.105795 |
| [9] |
HU Qiguo, GAO Zhan. System reliablity modeling in competitive failure considering zoned shock effect[J]. Journal of System Simulation, 2021, 33(5): 1070-1077. DOI:10.1016/0142-1123(96)82816-7 |
| [10] |
丁力, 蔡风景. 基于逆高斯过程的竞争失效模型[J]. 温州大学学报(自然科学版), 2021, 42(3): 38-48. DING Li, CAI Fengjing. Competitive failure model based on inverse Gaussian process[J]. Journal of Wenzhou University(Natural Science Edition), 2021, 42(3): 38-48. DOI:10.3875/j.issn.1674-3563.2021.03.005 |
| [11] |
张震宇. 压气机叶片TC4钛合金超高周疲劳失效机制及强度-寿命预测方法[D]. 北京: 北京理工大学, 2015 ZHANG Zhenyu. Fatigue failure mechanism and strength-life prediction method of TC4 titanium alloy for compressor blade in very high cycle regime[D]. Beijing: Beijing University of Technology, 2015 DOI: 10.1016/j.ijfatigue.2019.105365 |
| [12] |
DENG Hailong, LIU Hang, LIU Qichen, et al. Fatigue strength prediction of carburized 12Cr steel alloy: effects of evaluation of maximum crack sizes and residual stress distribution[J]. Fatigue & Fracture of Engineering Materials & Structures, 2020, 43(2): 342-351. DOI:10.1111/ffe.13149 |
| [13] |
DENG Hailong, LI Wei, SUN Zhenduo, et al. Multiple fatigue failure behaviors and long-life prediction approach of carburized Cr-Ni steel with variable stress ratio[J]. Materials, 2017, 10(9): 1084-1084. DOI:10.3390/ma10091084 |
| [14] |
MURAKAMI Y, ENDO M. Effects of defects, inclusions and inhomogeneities on fatigue strength[J]. International Journal of Fatigue, 1994, 16(3): 163-182. DOI:10.1016/0142-1123(94)90001-9 |
| [15] |
GE Shucan, LI Hailong, XU Tong, et al. Aspect sensitivity of double-layer polar mesosphere summer echoes at VHF based on an experimental case[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2021, 223: 105741. DOI:10.1016/J.JASTP.2021.105741 |
| [16] |
NOVOA M F. Goodness-of-fit tests for the bivariate Poisson distribution[J]. Communications in Statistics-Simulation and Computation, 2021, 50(7): 771-793. DOI:10.1080/03610918.2019.1590598 |
 2022, Vol. 30
2022, Vol. 30


