2. 河钢集团钢研总院,石家庄 050023;
3. 河钢集团邯钢公司技术中心,河北 邯郸 056002
2. HBIS Technology Research, Shijiazhuang 050023, China;
3. HBIS Hansteel, Handan 056002, China
随着市场对高强钢需求的日益增加,其强度级别也越来越高,快速冷却和超快速冷却逐渐成为提高钢材强度的主要手段[1]。快冷往往会在钢板加工过程中引入较大的残余应力,而残余应力的存在将影响高强钢的尺寸稳定性、疲劳寿命、抗腐蚀能力等性能[2]。在后续加工或使用过程中,由于部分内应力释放,残余应力也会导致材料畸变,甚至造成材料的开裂。因此,残余应力一直是高强钢工业生产及使用过程中的共性问题[3]。
残余应力是指在没有外力的情况下存在于材料内部的应力系统,其本质是由金属内部结构不均匀的塑性变形引起的。工件在常见的机械加工[4-5]和热处理过程[6]中都会伴随着残余应力的产生。在已有的研究中,对于残余应力的有效消除方法主要有机械拉伸法[7]、时效消除法[8]、热处理法[9-10]、振动消除法[11-13]及深冷处理[11]等。虽然这些方法均能够对残余应力起到很好的消除效果,但也都有各自的局限性。
为了解决钢材中由残余应力导致的问题,残余应力的表征和残余应力的调控[14]是目前的研究热点。在表征方面,由于残余应力具有整体平衡的特点,所以材料局部应力水平无法全面表征和预测残余应力的演变规律。然而,现有残余应力表征方法,如磁测法、X射线衍射法、盲孔法、裂纹柔度法[15]中多为局部应力的表征方法,无法反应残余应力的整体水平以及分布规律;同时,受组织结构以及碳化物析出的影响,采用晶格间距或磁致伸缩效应表征残余应力的方法存在一定程度的随机误差[16]。在调控方面,残余应力不均匀分布是导致材料畸变的主要因素[17],但现有研究尚未建立材料畸变的评价指标,现有高强钢制备工艺缺乏残余应力控制的理论支撑,工艺调控目标不明确。
现有的残余应力表征方法中,裂纹柔度法(CCM)可以准确表征带钢内部残余应力[18]。本文采用本课题组前期基于弹性断裂力学原理开发的裂纹柔度法残余应力测试计算系统,解决了高强钢内部厚度方向上残余应力的表征难题;结合本课题组前期开发的裂纹柔度法残余应力测试计算系统和ABAQUS有限元仿真软件,提出了将带钢“应力不平衡度”作为材料畸变评价指标;借助ABAQUS有限元分析,优化平整工艺参数,提高材料抗畸变的能力,以期为高强钢残余应力消除工艺优化提供理论基础。
1 实验 1.1 实验材料实验所用的材料为热轧卷取后的620JJ搅拌罐体用钢(卷号19IA16976300),其厚度为2.75 mm,宽度为1 500 mm,化学成分见表 1。
| 表 1 邯钢620JJ钢板化学成分表(质量分数/%) Table 1 Chemical composition of 620JJ steel (wt.%) |
采用裂纹柔度法检测板内部的残余应力,对于原始和平整工艺处理后的钢板,均在距离卷芯30 m处位置的轧卷处取1 500 mm×500 mm的宽板,从操作侧开始,以钢板宽度的1/2处为对称中心,分别在1/16,1/8,1/4,1/2宽度处取7块50 mm×60 mm的试样作为残余应力的测试样,取样示意图如图 1所示。
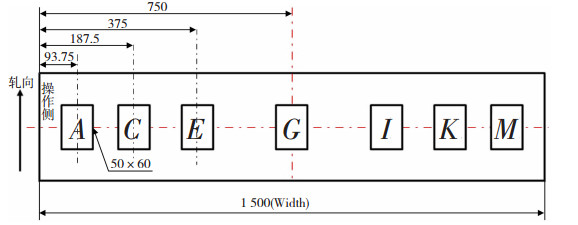
|
图 1 残余应力测点示意图(单位:mm) Fig.1 Residual stress measuring points |
为了更精确地反应试样内部沿厚度方向上的残余应力分布,本文采用裂纹柔度法(CCM)作为残余应力表征方法。图 2为裂纹柔度法测量应力示意图,为了避免试样在加工过程中引入的裂纹对测点处应力产生影响,本实验采用电火花线切割的方式在试样表面中间位置引入裂纹。电火花数控线切割机床为江苏泰州天龙数控机床有限公司生产的DK7745,线切割丝为Φ0.18 mm钼丝;应变片选用高精密级箔式酚醛-缩醛类BE120-3AA;用江苏东华测试公司的DH3818Y型静态应变仪采集应变数据,并用半桥法实现温度补偿。
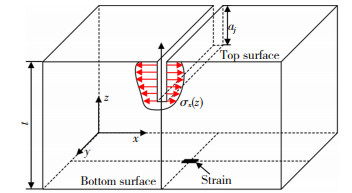
|
图 2 裂纹柔度法应变测量示意图 Fig.2 Strain measurement by crack compliance method |
假设高强钢残余应力仅沿待测钢板的厚度方向变化,沿长度、宽度方向均匀分布[18]。基于级数展开法,通过测量所得的应变值计算材料初始残余应力,能够有效降低测量应变引起的应力计算误差,故用一个级数展开式来描述未知的应力分布。
| $ \sigma_{x, y}(z)=\sum\limits_{i=1}^{n} A_{i} P_{i}(z) $ |
式中:Ai为待定系数;n为插值函数的阶数;Pi(z)为线性无关插值函数,为保证应力分布满足力和力矩的平衡条件,本文选用2至15阶勒让德多项式作为插值函数。
| $ \begin{gathered} P_{0}(z)=1 \\ P_{i}(z)=\frac{1}{2^{i} i !} \frac{d^{i}}{d_{z}^{i}}\left(z^{i}-1\right)^{i} \quad i=1, 2, \cdots \end{gathered} $ |
裂纹柔度法的关键部分是得到上述级数展开式的待定系数Ai,为了得到Ai,需要先进行以下计算。计算图 2切口背面处的应变随裂纹深度aj增加的响应值,即柔度函数(Ci(aj)),由叠加原理可用另外一个级数展开计算响应应变值。
| $ \varepsilon_{x, y}\left(a_{j}\right)=\sum\limits_{i=1}^{n} A_{i} C_{i}\left(a_{j}\right)=C A $ |
为使误差最小,将响应应变值与实测应变值进行最小二乘法拟合。
| $ \frac{\partial}{\partial A_{i}} \sum\limits_{j=1}^{m}\left[\varepsilon_{m}\left(a_{j}\right)-\sum\limits_{k=1}^{n} A_{k} C_{k}\left(a_{j}, P_{k}\right)\right]^{2}=0 $ |
式中m为试样的应变采集次数,且m≫n。通过对上述方程的运算,即可得到待定系数Ai。
| $ A_{i}=\left(C^{T} C\right)^{-1} C^{T} \varepsilon_{m}=B \varepsilon_{m} $ |
因此,选择适当的插值函数Pi(z)后,再求得待定系数Ai,即可计算出材料内部残余应力分布。
1.2.2 单下辊传动平整仿真模拟利用ABAQUS有限元软件对620JJ高强钢单下辊传动平整的残余应力进行仿真模拟。如图 3所示,为简化模型,提高计算速度,建模时将带钢在长度上截取一段,模型长度为2 000 mm,板宽为1 500 mm,厚度为2.75 mm。钢板垂直方向的自由度受到限制,钢板在被咬入轧辊之后仅受轧辊的摩擦力向前运动,轧辊与钢板间的摩擦系数取0.15,平整的轧制力为4 500 kN。轧辊辊径取500 mm,自由度被限制为仅能够沿辊轴方向旋转,下辊为主动辊,以6.28 rad/s的角速度顺时针匀速旋转,上辊为自由旋转的从动辊。

|
图 3 ABAQUS模拟620JJ高强钢单下辊传动平整计算模型 Fig.3 ABAQUS simulation of calculation model of 620JJ high-strength steel under single bottom roller driven flattening |
平整前后钢板的残余应力分布如图 4所示。由图 4(a)、(b)、(d)可以看出,平整前钢板沿厚度方向的残余应力呈“W”形分布,拉压应力交替。在试样的侧边部(A、E、K点),如图 4(a)、(b)、(d),试样上下边部以及试样芯部的应力皆呈压应力状态,其余部分呈拉应力状态。测试点A、E、K上表面的应力分别为:58.66、463.26和7.62 MPa,下表面的应力分别为:-201.61、-47.28和-226.93 MPa,其中拉应力以正值表示,压应力以负值表示。图 4(c)是试样宽度1/2处G点的残余应力分布,此处的芯部应力呈拉应力状态,与试样侧边部(A、E、K点)的应力分布不同,上下表面都为压应力,应力大小分别为-78.01和-35.78 MPa。
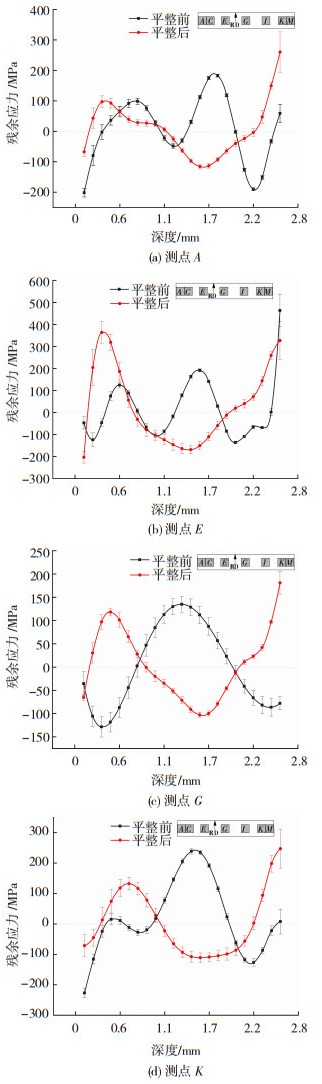
|
图 4 平整前后试样厚度方向残余应力分布 Fig.4 Residual stress distribution along thickness direction of plate before and after flattening: (a) measuring point A; (b) measuring point E; (c) measuring point G; (d) measuring point K |
图 4表示平整前后带钢厚度方向的残余应力分布。由图 4可以看到,经过平整后带钢厚度方向残余应力曲线呈“U”形分布,经过平整的每一个试样,上下表面的应力状态均相反,下表面均为压应力状态,上表面均为拉应力状态,且在下边部的次表面处都有一个拉应力波峰。在带钢上下边部以外的部分,带钢板厚方向上应力的最大值由463.26 MPa降至363.6 MPa,降幅为22%;而在上下表面和次表面处,应力的最大值由238.47 MPa升高至260.06 MPa。
2.2 平整前后带钢宽度方向应力分布图 5为平整前后钢板上下表面宽度方向的应力分布,表 2为平整前后板宽方向上下表面的应力极值及其差值。从图 5和表 2中可以看到,平整前带钢上表面各点残余应力的幅值较大,为572.35 MPa,经过平整后降至267.38 MPa,下降了53.28%;下表面的残余应力幅值由平整前的437.84 MPa降至392.39 MPa,下降了10.38%;经过平整工艺后,带钢上表面应力极值从463.26 MPa降至331.05 MPa,下降了28.54%,下表面应力极值从210.91 MPa降至189.08 MPa,下降了10.35%。
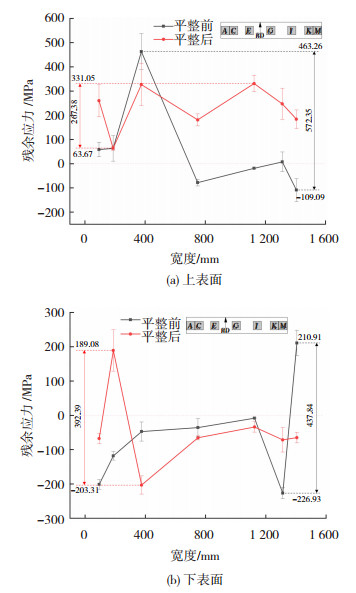
|
图 5 平整前后板宽方向上的表面应力分布 Fig.5 Surface stress distribution along width direction of plate before and after flattening: (a) upper surface; (b) lower surface |
| 表 2 平整前后带钢上下表面应力极值及其差值 Table 2 Extreme value and difference of stress on upper and lower surfaces of strip before and after flattening |
以弹性应变能(ERS)[18]表征带钢宽度方向残余应力的总体水平,弹性应变能是对残余应力绝对值积分后所得,其公式为
| $ E_{\mathrm{RS}}=\int_{0}^{x}\left|\sigma_{\mathrm{RS}}\right| \mathrm{d} x $ |
式中:ERS为带钢内部残余应力的单位弹性应变能,MPa·mm;σRS为带钢内部残余应力值,MPa。
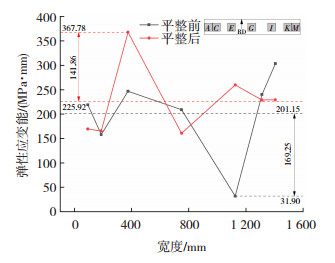
图 6为平整前后带钢宽度方向上的弹性应变能,可以看到:平整后板宽方向平均弹性应变能水平有所提高,从201.15 MPa·mm提高到225.92 MPa·mm,提高了12.31%;弹性应变能的不平衡度有所改善,平整前各测点弹性应变能与平均弹性应变能的最大差值为169.25 MPa·mm,平整后此差值降低为141.86 MPa·mm,降低了16.18%。
|
图 6 平整前后带钢宽度方向弹性应变能 Fig.6 Elastic strain energy along width direction of strip before and after flattening |
板形缺陷是指在带钢的制备、加工过程中出现的平直度缺陷[19-20],而出厂时具有良好板形的带钢在下游使用过程中会出现变形,这种材料下游使用过程中出现的变形被称作畸变。带钢发生畸变的可能性与带钢内部残余应力的分布有直接关联[17]。通过观察和测量发生畸变的钢板中残余应力的分布,发现上下板面的应力不平衡会导致带钢发生翘曲,板宽方向应力不平衡则会导致带钢侧弯[21],下游加工的不同方式也会对钢板引入不同程度的应力,影响钢板畸变的可能性。
针对带钢内部残余应力分布影响钢板畸变的可能性,本文定义“应力不平衡度”,并将其作为带钢产生畸变的评价指标。带钢厚度方向“应力不平衡度”为带钢上下边部区间应变能差值的绝对值与材料的屈服强度的比值,其公式为
| $ B T_{\mathrm{E}}=\frac{\left|\int_{0}^{0.3} \sigma_{\mathrm{RS}} \mathrm{d} h-\int_{0.7}^{1} \sigma_{\mathrm{RS}} \mathrm{d} h\right|}{\int_{0}^{-1} \sigma_{\mathrm{s}} \mathrm{d} h} \times 100 \% $ |
式中:BTE为带钢应力不平衡度;σRS为带钢内部残余应力值,MPa;σs为带钢屈服强度,MPa。应力不平衡度越大,带钢越容易发生板形缺陷和畸变。
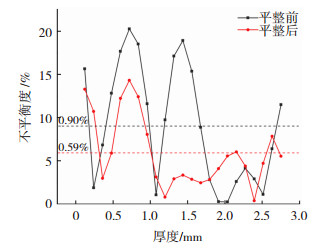
3.2 平整加工对应力不平衡度及残余应力变化率的影响平整工艺影响带钢应力不平衡度和残余应力变化率的主要作用是应力均衡化。图 7和表 3为带钢平整前后板宽和板厚方向的应力不平衡度。从图 7中可知经过平整以后,板宽方向整体不平衡度从0.90%降至0.59%,结合图 6中板宽方向弹性应变能的变化,可以发现带钢板宽方向整体的不平衡度和残余应力变化率均有所下降。板厚方向测点E和测点G的应力不平衡度波动幅度在12%左右;测点I的应力不平衡度上升了131.56%;其余测点处的应力不平衡度均有大幅下降,平均降幅为57.14%。尽管测点I的应力不平衡度波动幅度很大,但无论带钢是否平整,其应力不平衡度的数值都很低,I点应力不平衡度上升是应力均衡化造成的结果,而使带钢内部应力均衡化的主要原因在于平整过程带钢的变形机制。
|
图 7 平整前后带钢宽度方向应力不平衡度 Fig.7 Stress unbalance along width direction of strip before and after flattening |
| 表 3 平整前后带钢厚度方向应力不平衡度及变化率 Table 3 Stress unbalance and change rate along thickness direction of strip before and after flattening |
平整过程是一种非均匀塑性变形过程,相比轧制工艺,平整工艺的轧制力很小,小轧制力无法使带钢芯部的滑移系开动,带钢在轧制摩擦力的作用下发生表层塑性变形,变形由表面向芯部传递,因此,平整工艺导致的带钢内部的应力状态与轧制工艺相反。由于平整产生的残余应力属于宏观残余应力,可以与外力叠加[21-25],形成应力均衡化的效果。对于原始带钢中应力不平衡度低的区域,平整的应力均衡化会适度增加该区域的应力不平衡度;对于带钢整体,平整可以有效改善带钢的不平衡度。
3.3 改善带钢上下表面应力不平衡度针对上述导致应力不平衡的因素,从单辊传动及双辊传动对畸变的影响、摩擦力及张力对畸变的影响和轧制压力对畸变的影响,本文利用ABAQUS有限元模拟软件进行平整工艺优化探究。
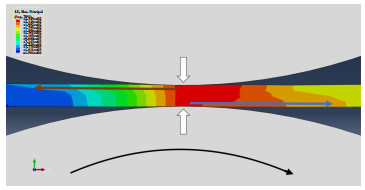
3.3.1 传动方式对畸变的影响带钢经过单下辊传动平整机进行平整,图 8为ABAQUS模拟单下辊/双辊平整后带钢的受力示意图。由图 8可知,带钢的运动仅依靠下辊的摩擦力,带钢上下表面受到的摩擦力方向相反,因此,带钢下表面的延伸就会大于上表面,这将导致带钢上下表面应力不平衡。在图 4中可以看到,带钢厚向残余应力也不平衡,每个测点带钢都为上拉下压状态,上下表面应力分别为-67.53/260.06 MPa、-203.21/326.89 MPa、-65.3/181.01 MPa、-71.4 /247.22 MPa,这是由于平整工艺与单下辊传动产生的残余应力叠加导致的。
|
图 8 ABAQUS模拟单下辊/双辊平整后带钢的受力示意图 Fig.8 ABAQUS simulation of force on strip after single/double roll flattening |
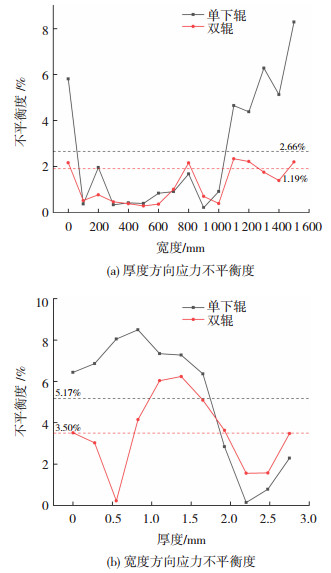
将传动方式改为双辊传动可以有效改善由于单辊传动导致的高应力不平衡度问题。图 9为ABAQUS模拟单下辊/双辊平整后带钢厚向和宽向的应力不平衡度,可以看到,将传动方式改为双辊传动后,带钢厚度方向和宽度方向上的应力不平衡度均有下降。由图 9(a)可知,厚度方向的平均应力不平衡度从2.66%降至1.19%,降幅为55.26%,说明双辊传动平整缓解了带钢宽向的高应力不平衡度,这样就减少了带钢发生C翘的可能性;由图 9(b)可知,宽度方向平均应力不平衡度从5.17%降至3.50%,降幅为32.30%。传动方式是影响带钢整体应力不平衡度的主要原因,传动方式改为双辊传动后,带钢整体应力不平衡度降低,带钢发生畸变的可能性同时降低。
|
图 9 ABAQUS模拟单下辊/双辊平整后带钢应力不平衡度 Fig.9 ABAQUS simulation of stress unbalance of strip after single/double roll flattening: (a) stress unbalance in thickness direction; (b) stress unbalance in width direction |
由于带钢在平整过程前后分别会经历开卷和卷取,所以在平整时带钢头部及尾部有张力;平整过程中轧辊与带钢之间的摩擦力也会对平整后带钢畸变产生影响。ABAQUS有限元模拟中,初始摩擦系数为0.15,变更后的摩擦系数为0.3;模拟开卷机和卷取机对带钢施加的张力,取前张力为7 kN,后张力为20 kN,厚度方向应力不平衡度的测点位置与1.2小节残余应力测点位置相同。
增加摩擦力或者张力均可有效改善带钢宽向应力不平衡度,对带钢厚向应力不平衡度改善效果不明显。图 10是在ABAQUS模拟增加摩擦力或张力前后,单下辊/双辊传动平整带钢厚向和宽向的应力不平衡度,可以看到,宽度方向上,单下辊传动时增加摩擦力使宽向平均不平衡度从5.17%下降至3.36%,增加张力使宽向平均不平衡度下降至2.20%;双辊传动时增加摩擦力使宽向平均不平衡度从3.50%下降至1.21%,增加张力使宽向平均不平衡度下降至2.44%。厚度方向上,单下辊传动时增加摩擦力使厚向平均不平衡度从3.17%下降至1.61%,增加张力使宽向平均不平衡度上升至4.08%;双辊传动时增加摩擦力使厚向平均不平衡度由1.19%上升至5.28%,增加张力使宽向平均不平衡度上升至2.75%。

|
图 10 ABAQUS模拟增加摩擦系数及张力前后单下辊/双辊平整带钢应力不平衡度 Fig.10 ABAQUS simulation of stress unbalance of strip under single/double roll flattening before and after increasing friction coefficient and tension: (a) stress unbalance in width direction under single roll flattening; (b) stress unbalance in width direction under double roll flattening; (c) stress unbalance in thickness direction under single roll flattening; (d) stress unbalance in thickness direction under double roll flattening |
适度增加轧制力可以减小平整后带钢出现畸变的可能性。图 11为ABAQUS模拟增加轧制力前后单下辊/双辊传动平整带钢厚向和宽向的应力不平衡度,有限元模型中将轧制压力从4 500 kN提升到5 600 kN。从图 11可以看到,增加轧制力后,高应力不平衡度的部分减小,小应力不平衡度的部分适度增大,平整的应力均衡化效果进一步提升;厚度方向单辊/双辊平整平均应力不平衡度分别下降了53.37%和37.74%,宽度方向单辊/双辊平整平均应力不平衡度分别下降了40.62%和28.57%。

|
图 11 ABAQUS模拟增加轧制力前后单下辊/双辊平整带钢应力不平衡度 Fig.11 ABAQUS simulation of stress unbalance of strip under single/double roll flattening before and after increasing rolling force: (a) stress unbalance in thickness direction under single roll flattening; (b) stress unbalance in thickness direction under double roll flattening; (c) stress unbalance in width direction under single roll flattening; (d) stress unbalance in width direction under double roll flattening |
带钢变形幅度加剧和金属流动性的增加是造成应力均衡化效果进一步提升的原因。增加轧制力后,带钢在轧辊处发生的表面塑性变形程度增加,变形由表面向芯部传递后,带钢内部金属在平整过程中流动的幅度加剧。因此,增加轧制力后,平整工艺导致应力状态更显著,更大的平整导致残余应力与平整前的残余应力叠加,形成应力均衡化的效果更为明显,平均应力不平衡度的下降也表明,增加轧制力后能够有效降低平整后带钢出现畸变的可能性。
4 结论本文通过裂纹柔度法测量带钢内部整体残余应力,分析了平整后高强钢产生畸变的原因,根据残余应力在厚度或板宽方向分布不均将导致带钢发生畸变,将“应力不平衡度”作为畸变评价指标,并基于应力不平衡度分析了平整工艺对带钢内部残余应力分布和畸变的影响,结合ABAQUS有限元模拟探索了提高高强钢抗畸变能力的平整加工优化方案。
1) 裂纹柔度法可以准确地表征带钢内部的残余应力及其分布。经过平整后,带钢厚度方向的残余应力曲线呈“U”形分布,且下表面受压,下边部次表面处有一个拉应力波峰,带钢内部残余应力的最大值由463.26 MPa降至363.6 MPa;而带钢边部残余应力的最大值由238.47 MPa上升至260.06 MPa。宽度方向的残余应力水平用弹性应变能来表示,平整后板宽方向平均弹性应变能有所提高,从201.15 MPa·mm提高到225.92 MPa·mm; 弹性应变能的不平衡度有所改善,平整前后各测点弹性应变能与平均弹性应变能的最大差值降低了16.18%。
2) 带钢内部残余应力分布是影响钢板畸变可能性的原因,本文定义带钢应力不平衡度作为畸变评价指标,是由于应力不平衡度可以直观地表征带钢发生板形缺陷和下游加工产生畸变的可能性。平整加工对带钢应力不平衡度和畸变的主要影响是应力的均衡化。
3) 从轧辊传动方式、摩擦力及张力、轧制压力3个方向优化工艺参数。ABAQUS模拟传动方式从单辊改为双辊传动后,带钢厚向及宽向应力不平衡度分别下降了55.26%和32.30%;增加摩擦力或张力均可有效改善带钢宽向应力不平衡度,对带钢厚向应力不平衡度改善效果不明显;增加轧制力后,平整的应力均衡化效果进一步提升,厚度方向单辊/双辊平整使平均应力不平衡度分别下降了53.37%和37.74%,宽度方向单辊/双辊平整平均应力不平衡度分别下降了40.62%和28.57%。
| [1] |
王国栋. 新一代TMCP技术的发展[J]. 轧钢, 2012, 29(1): 1-8. WANG Guodong. Development of a new generation of TMCP technology[J]. Steel Rolling, 2012, 29(1): 1-8. DOI:10.3969/j.issn.1003-9996.2012.01.001 |
| [2] |
邱增帅, 何安瑞, 邵健, 等. 冷却工艺对热轧高强带钢残余应力的影响[J]. 中南大学学报(自然科学版), 2018, 49(6): 1373-1380. QIU Zengshuai, HE Anrui, SHAO Jian, et al. Effect of cooling process on residual stress of hot-rolled high-strength strip steel[J]. Journal of Central South University (Science and Technology), 2018, 49(6): 1373-1380. DOI:10.11817/j.issn.1672-7207.2018.06.009 |
| [3] |
龚海. 铝合金厚板内应力演变规律及残余应力场评估模型研究[D]. 长沙: 中南大学, 2011. GONG Hai. Study on internal stress evolution law and residual stress field evaluation model of aluminum alloy thick plate[D]. Changsha: Central South University, 2011. DOI: 10.7666/d.y2198030 |
| [4] |
ALMEN J O, BLACK P H, DOLAN T J. Residual stresses and fatigue in metals[J]. Journal of Applied Mechanics, 1964, 31(2): 368-369. |
| [5] |
LEE Y S, DAWSON P R. Obtaining residual stresses in metal forming after neglecting elasticity on loading[J]. 1989, 56(2): 318-327.
|
| [6] |
钟士红. 钢的回火工艺和回火方程[M]. 北京: 机械工业出版社, 1993: 11-15.
|
| [7] |
BRINKSMEIER E, HANNOVER, CAMMETT J T, et al. Residual stress-measurement and cause in machining process[J]. Cirp Annals Manufacturing Technology, 1982, 31(2): 491-510. DOI:10.1016/S0007-8506(07)60172-3 |
| [8] |
杨新华, 杨国华. 振动时效在大型焊接结构件中的应用[J]. 热加工工艺, 2012, 41(16): 210-212. YANG Xinhua, YANG Guohua. Application of stress relief by vibration on large welded structure[J]. Hot Working Technology, 2012, 41(16): 210-212. |
| [9] |
张根保, 张坤能. 残余应力消除技术[J]. 制造技术与机床, 2015, 70(4): 6-11. ZHANG Genbao, ZHANG Kunneng. Technology of eliminating residual stresses[J]. Manufacturing Technology & Machine Tool, 2015, 70(4): 6-11. DOI:10.3969/j.issn.1005-2402.2015.04.002 |
| [10] |
杨延功, 焦启林. 消除焊接残余应力的四种方法[J]. 工程机械与维修, 2009(9): 172-173. YANG Yangong, JIAO Qilin. Four ways to eliminate welding residual stress[J]. Construction Machinery & Maintenance, 2009(9): 172-173. DOI:10.3969/j.issn.1006-2114.2009.09.041 |
| [11] |
王秋成, 柯映林. 航空高强度铝合金残余应力的抑制与消除[J]. 航空材料学报, 2002, 2(3): 59-62. WANG Qiucheng, KE Yinglin. Control and relief of residual stresses in high-strength aluminum alloy parts for aerospace industry[J]. Journal of Aronautical Materials, 2002, 2(3): 59-62. DOI:10.3969/j.issn.1005-5053.2002.03.015 |
| [12] |
王旻沁, 华云松. 振动时效技术的研究现状与发展趋势[J]. 机械制造, 2011, 49(1): 66-69. WANG Minqin, HUA Yunsong. Research status and development of vibration stress relief[J]. Machinery, 2011, 49(1): 66-69. DOI:10.3969/j.issn.1000-4998.2011.01.025 |
| [13] |
张晓, 杜战峰. 振动时效在铝合金零件加工中的应用[J]. 新技术新工艺, 2008(7): 56-58. ZHANG Xiao, DU Zhanfeng. The application of vibration aging in the processing of aluminum alloy parts[J]. New Technology & New Process, 2008(7): 56-58. DOI:10.3969/j.issn.1003-5311.2008.07.018 |
| [14] |
JAMESM N. Residual stress influences on structural reliability[J]. Engineering Failure Analysis, 2011, 18(8): 1909-1920. DOI:10.1016/j.engfailanal.2011.06.005 |
| [15] |
苏愿晓, 张清东, 曾杰伟. 高强度钢板残余应力消减方法研究[C] //中国金属学会. 第十届中国钢铁年会暨第六届宝钢学术年会论文集. 2015: 1-6. SU Yuanxiao, ZHANG Qingdong, ZENG Jiewei. Research on reducing method of residual stress of high strength steel plate[C] // The Chinese Society for Metals. Proceedings of the 10th CSM Steel Congress & the 6th Baosteel Biennial Academic Conference. 2015: 1-6. |
| [16] |
李文涛, 林振铭, 汪宏斌, 等. 冷轧带钢退火处理中残余应力变化规律研究[J]. 上海金属, 2016, 38(1): 42-45, 54. LI Wentao, LIN Zhenming, WANG Hongbin, et al. Study on the change law of residual stress in annealing of cold rolled strip steel[J]. Shanghai Metals, 2016, 38(1): 42-45, 54. DOI:10.3969/j.issn.1001-7208.2016.01.010 |
| [17] |
DONG Fei, YI Youping, HUANG Shiquan. Measuring the internal residual stress of aluminum-copper alloy forgings by using the crack compliance method with optimized parameters[J]. Journal of Central South University, 2020, 27(11): 3163-3174. DOI:10.1007/s11771-020-4538-0 |
| [18] |
丁文红. 高强钢连续冷却及退火过程残余应力演变规律研究[D]. 北京: 北京科技大学, 2020. DING Wenhong. Study on the evolution of residual stress during continuous cooling and annealing of high-strength steel[D]. Beijing: University of Science and Technology Beijing, 2020. |
| [19] |
杨立庆, 饶静, 邓杭州, 等. 安钢1780mm热连轧平整板形缺陷分析与改进[J]. 特钢技术, 2019, 25(4): 60-63. YANG Liqing, XIAO Jing, DENG Hangzhou, et al. Analysis and improvement of shape defects in anyang steel's 1780 mm hot strip rolling[J]. Special Steel Technology, 2019, 25(4): 60-63. DOI:10.16683/J.CNKI.ISSN1674-0971.2019.4067 |
| [20] |
昝现亮, 王凤琴, 刘子英, 等. 热轧带钢残余应力相关板形缺陷机理分析及攻关措施[J]. 中国冶金, 2020, 30(5): 35-41, 64. ZAN Xianliang, WANG Fengqin, LIU Ziying, et al. Mechanism analysis and countermeasures of strip shape defects related to residual stress of hot-rolled strip steel[J]. China Metallurgy, 2020, 30(5): 35-41, 64. DOI:10.13228/j.boyuan.issn1006-9356.20190515 |
| [21] |
丁文红. 平整机的板形改善机制及其应用[J]. 轧钢, 2012, 29(1): 26-28, 52. DING Wenhong. Plate shape improvement mechanism of leveling machine and its application[J]. Steel Rolling, 2012, 29(1): 26-28, 52. DOI:10.3969/j.issn.1003-9996.2012.01.007 |
| [22] |
丁韦, 高振坤, 宋宏图, 等. 残余应力对贝氏体钢轨使用缺陷的影响[J]. 铁道建筑, 2021, 61(6): 116-120. DING Wei, GAO Zhenkun, SONG Hongtu, et al. Influence of residual stress on bainite rail use defects[J]. Railway Engineering, 2021, 61(6): 116-120. DOI:10.3969/j.issn.1003-1995.2021.06.26 |
| [23] |
马文静, 陈志国, 李鸿娟, 等. 新型热处理调控Al-Cu-Mg合金残余应力的工艺和机理[J]. 材料研究学报, 2019, 33(6): 435-442. MA Wenjing, CHEN Zhiguo, LI Hongjuan, et al. Process and mechanism of novel heat treatment for controlling residual stress in Al-Cu-Mg alloy[J]. Chinese Journal of Materials Research, 2019, 33(6): 435-442. DOI:10.11901/1005.3093.2018.626 |
| [24] |
胡盛德, 刘勇, 贾余超, 等. 厚壁型钢冷弯应力分析[J]. 武汉科技大学学报(自然科学版), 2012, 35(3): 174-177, 185. HU Shengde, LIU Yong, JIA Yuchao, et al. Stress analysis of thick-wall cold-bent profiled steel[J]. Journal of Wuhan University of Science and Technology (Natural Science Edition), 2012, 35(3): 174-177, 185. DOI:10.3969/j.issn.1674-3644.2012.03.004 |
| [25] |
钟雯, 丁幼亮, 宋永生, 等. 顶板-纵肋焊接细节残余应力的松弛效应[J]. 浙江大学学报(工学版), 2020, 54(1): 83-90. ZHONG Wen, DING Youliang, SONG Yongsheng, et al. Relaxation effect of welding residual stress in deck-to-rib joints[J]. Journal of Zhejiang University(Engineering Science), 2020, 54(1): 83-90. DOI:10.3785/j.issn.1008-973X.2020.01.010 |
 2022, Vol. 30
2022, Vol. 30


