2. 大连康丰科技有限公司,辽宁 大连 116028
2. Dalian Konform Technical Company Ltd., Dalian 116028, China
近年来,我国在连续挤压技术方面取得巨大发展,尤其是在铜材连续挤压技术上,已处于世界领先地位[1]。随着在连续挤压技术中铜排逐步的产业化生产,模具生产方式与工艺流程得到不断改善[2]。为了满足市场的需求,铜排产品逐渐趋向于更宽、更薄,因此使用连续挤压技术生产大宽厚比铜排是目前企业需要解决的一大难题[3]。
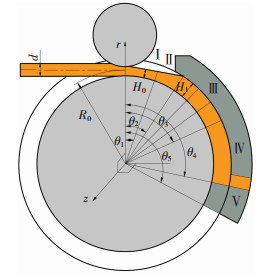
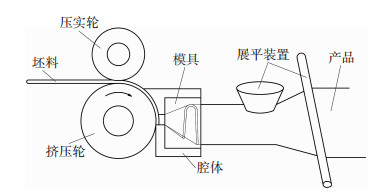
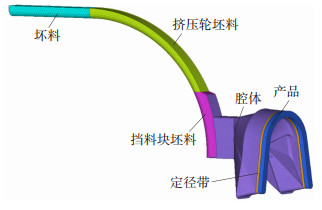
利用连续挤压方法将圆形铜杆挤压成U型铜材,再经过展平装置展平为平板带,即U型铜带连挤连展技术的生产方法,如图 1所示。坯料经过压实轮被送入挤压轮沟槽内,在挤压轮沟槽表面摩擦力的驱动作用下进入腔体进料口,而后通过与腔体进料口相连的U型环锥台通道进入模具定径带挤压成U型板带,U型板带再通过展平装置展平成板带坯,板带坯料经过卷曲装置得到成卷的板带,最后将成卷的板带进行处理后形成铜带成品[4]。
|
图 1 U型连挤连展铜带示意图 Fig.1 Schematic diagram of U-shaped copper strip by continuous extrusion and continuous flattening |
U型连挤连展技术可以获得直径扩展比大于15的铜带产品,具有短流程、低成本、节能环保、经济效益高的特点,适合生产T2、T3类紫铜带[5]。此技术与直板连续挤压技术生产铜带相比,U型连续挤压带坯各点至腔体进料口中心距离基本相等,变形量和温度均匀,可使腔体内各部分金属流速更加均匀,而且整个带坯处于三向压应力状态下[6],挤压过程金属发生再结晶得到细晶粒组织,使各个方向机械性能更加均匀[7]。
针对各参数比对连续挤压产品成形性能的影响,国内外相关专家学者已进行了大量研究与理论分析。郭华仲等[8]研究了坯料直径对铜扁线连续挤压的影响,初步确定了坯料直径和金属塑性变形的关系,为连续挤压工模具设计提供了理论依据。宋宝韫等[9]利用主应力法得到了腔体入口单位挤压力与扩展比及产品厚度的关系。于孟等[10]采用工程法对连续挤压铜排的力能进行了计算, 得到了模腔入口挤压应力的解析表达式及挤压应力随产品厚度和宽厚比变化的规律。赵颖等[11]研究了产品宽厚比对焊合过程的影响,研究表明,随产品宽厚比的增加,焊合面上的焊合压力、焊合温度、等效应变速率和焊合速度均显著提高。徐宁宁等[12]通过分析扭-挤成形工艺金属流动和变形区特点, 建立了镁合金扭-挤成形载荷的主应力法求解模型。Cao等[13]采用主应力法建立各区力平衡方程, 计算得到纯铝和铝钛硼合金带扩展腔连续挤压的变形力。Yun等[14]通过塑性力学理论计算,建立了轧辊转速与挤压轮转速、压下量和板带尺寸等参数之间的协调方程。Lu等[15]分析了挤压工艺参数对组织演变的影响,提出挤压管的晶粒尺寸随初始温度和挤压速度的增加而增大,随挤压比的增大而减小。Devendra等[16]基于双因素三水平中心组合旋转设计,建立了连续挤压膨化原料力学性能预测的数学模型,并利用方差分析技术进行了验证。综上研究表明,可以利用解析法建立平衡方程,解决连续挤压过程中变形力等问题。
本文通过有限元模拟和解析计算相结合,研究了不同参数比对产品流速分布、模具型腔压力、挡料块压力、挤压轮扭矩的影响规律。利用HyperXtrude软件分析了不同参数比对模具出口处产品流动速度的影响规律,通过解析法建立了挡料块载荷与挤压轮扭矩的函数模型,以期为U型铜带极限尺寸的确定提供理论参考。
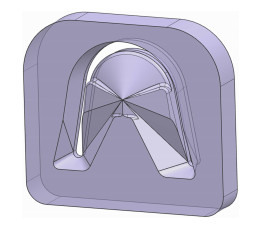
1 模拟参数设定U型铜带连续挤压的腔体模型如图 2所示,进料口高度为90 mm。坯料选用Φ30 mm的铜杆,基于TLJ630连续挤压机进行模拟,初始模具模型如图 3所示,U型展平宽度b为420 mm,厚度t为14 mm。模具材料为H13钢,材料的相关参数如表 1所示,模拟设定参数如表 2所示。定径带和模腔部位采用的摩擦类型为Coulomb摩擦,摩擦系数选取0.3,腔体热传导系数为3 000 W/(m2·℃),其余各部位皆采用滑动摩擦。网格划分后的有限元模型如图 4所示。

|
图 2 腔体模型 Fig.2 Cavity model |
|
图 3 模具模型 Fig.3 Mold model |
| 表 1 纯铜和H13钢的性能参数 Table 1 Performance parameters of pure copper and H13 steel |
| 表 2 模拟设定参数 Table 2 Simulation setting parameters |
|
图 4 有限元模型 Fig.4 Finite element model |
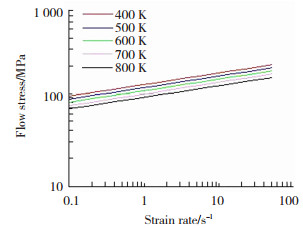
对于纯铜材料,在HyperMesh有限元中采取的本构关系曲线如图 5所示。
|
图 5 纯铜本构关系 Fig.5 Constitutive relationship of pure copper |
挤压比是表示金属变形量大小的参数,扩展比用来描述连续挤压中的扩展变形过程,宽厚比是壁板类产品的一个重要参数。本文主要研究厚度挤压比、直径扩展比、产品宽厚比对模具出口处的流速分布、模腔压力、挡料块载荷和挤压轮扭矩的影响。
| $ \text { 厚度挤压比, } \lambda_{1}=\frac{d}{t} \\ \text { 直径扩展比, } \lambda_{2}=\frac{b}{d} \\ \text { 产品宽厚比, } \lambda_{3}=\frac{b}{t} $ |
式中:t为产品厚度;b为展平宽度;d为坯料直径(单位:mm).
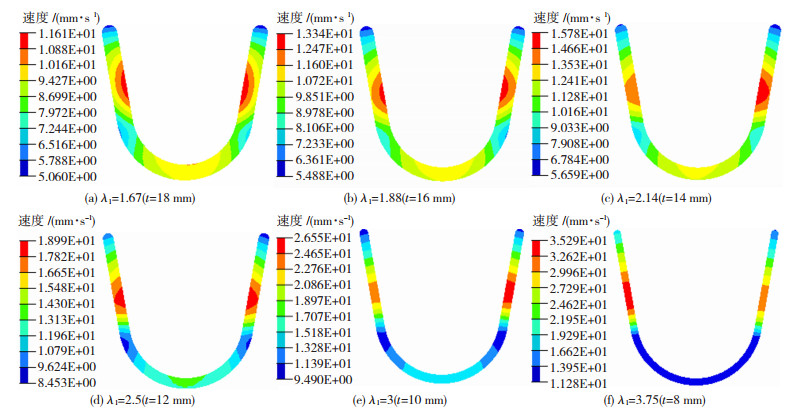
2.1 厚度挤压比λ1对产品速度的影响对坯料直径(d)为30 mm,展平宽度(b)为420 mm,产品厚度(t)为10、12、14、16、18 mm的铜带进行数值模拟, 结果如图 6所示。由图 6可以观察到厚度挤压比λ1变化时模具出口处金属流速分布的变化趋势。随着产品厚度t的增大,U型铜带速度分布越来越均匀,当λ1为3.75时,最大速度为35.29 mm/s,λ1为1.67时,最大速度为11.61 mm/s。金属在挤压进型腔后,由于模具内部的分流结构,导致金属优先向两侧填充,从而呈现出两侧金属流动速度快,圆弧处金属流动速度慢的趋势。
|
图 6 速度分布云图 Fig.6 Velocity distribution cloud map |
模具出口处产品流速分布的均匀性直接影响板带能否顺利成形,并进一步加工成为合格产品。为了更准确地比较不同型腔结构U型模具挤压出的产品流速均匀性,本文使用流速均方差(SDV)指标来衡量产品流速的均匀性,SDV值越小,表明产品的流速均匀性越好,反之则越差。
| $ \mathrm{SDV}=\sqrt{\frac{\sum_{i=1}^{N}\left(v_{i}-v_{\mathrm{a}}\right)^{2}}{N}} $ |
式中: N为板材截面区域选取的节点数目;vi为型材截面区域的节点速度;va为节点速度平均值。
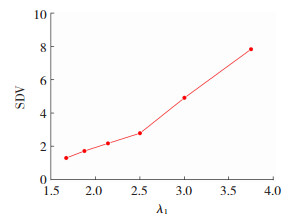
图 7为SDV随厚度挤压比λ1的变化曲线,可以看到,λ1小于2.5时,SDV值增加趋势缓慢;λ1大于2.5时,SDV值增幅明显,挤压比过大时出口产品的流速分布过于不均匀。
|
图 7 SDV随厚度挤压比λ1的变化 Fig.7 Changes in SDV with thickness extrusion ratio λ1 |
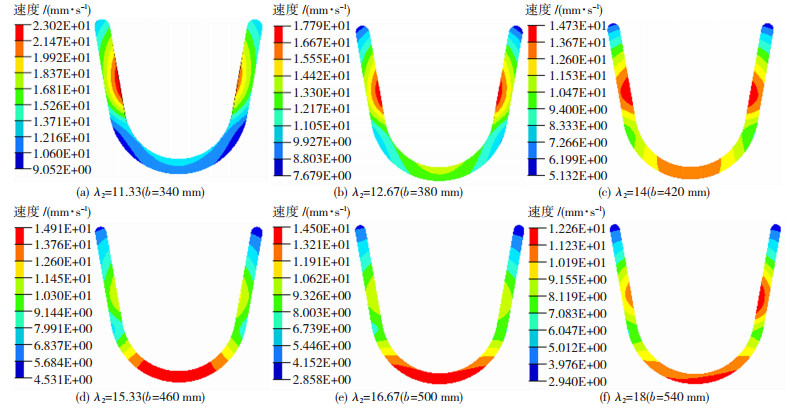
对坯料直径d为30 mm,产品厚度t为14 mm,展平宽度b为340、380、420、460、500、540 mm的铜带进行数值模拟。图 8为直径扩展比λ2的变化对产品流速分布的影响,λ2从11.33增加到18,最大流动速度从23.02 mm/s降低到12.26 mm/s。由图 8可以看到:当λ2小于14时,流速最快部位集中在U型两侧;λ2大于14时,流速最快部位则分布在圆弧处,且U型两端顶部流速过小,低于3 mm/s。
|
图 8 速度分布云图 Fig.8 Velocity distribution cloud map |
本研究模拟时发现,进料口中心至U型各部位距离基本相同,可保证各处流速分布基本均匀,而宽度过大时,进料口中心至两直边底端的距离要大于至圆弧区域的距离,使得圆弧区流速变快,因此,λ2变大时高流速区域逐渐从两侧转移至圆弧区。图 9中SDV值随λ2的增加先降低,后升高再降低,变化范围不大。
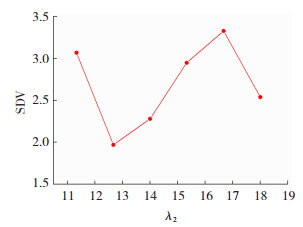
|
图 9 SDV随直径扩展比λ2的变化 Fig.9 Changes in SDV with diameter expansion ratio λ2 |
坯料通过挤压轮的摩擦作用从进料口进入型腔,通过U型模具挤压出合格产品。图 10为型腔内各区域划分部分,Ⅰ区为进料口区,Ⅱ区为型腔扩展区,Ⅲ区为模具挤压区。Ⅲ区腔体内形状相对复杂,在计算模具型腔压力时可简化成大U挤压出小U,利用主应力法求解模具腔体内的压应力值相比有限元模拟结果更为准确,选取A、B、C的3个截面对Ⅲ区进行切元计算,图 11为Ⅲ区型腔切元计算示意图。

|
图 10 型腔划分区域 Fig.10 Cavity division zones |
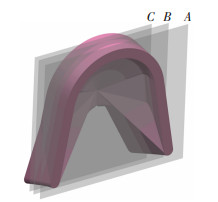
|
图 11 Ⅲ区型腔切元示意图 Fig.11 Schematic diagram of cavity cut elements in zone Ⅲ |
挤压过程中,U型模具型腔内Ⅲ区金属变形情况如图 12所示,在挤压变形区中切取厚度为dx的基元体,圆锥区在x轴方向的应力微分平衡方程为
| $ \left(\sigma_{x}+\mathrm{d} \sigma_{x}\right) \cdot S_{2}-\sigma_{x} \cdot S_{1}-\tau l \mathrm{~d} x-\sigma_{n} l \tan \alpha \mathrm{d} x=0 $ | (1) |
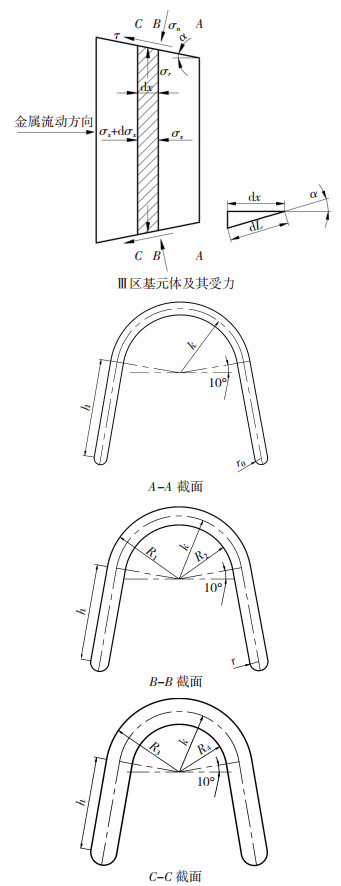
|
图 12 主应力法求解挤压力计算模型 Fig.12 Calculation model of extrusion force by principal stress method |
径向的应力平衡方程为
| $ \sigma_{n} \cos \alpha l \mathrm{~d} L-\sigma_{r} l \mathrm{~d} x-\tau l \mathrm{~d} L \sin \alpha=0 $ | (2) |
基元体右侧截面表面积为
| $ S_{1}=\frac{4}{9} \pi\left(R_{1}^{2}-R_{2}^{2}\right)+4 r h+\pi r^{2} $ | (3) |
基元体左侧截面表面积为
| $ \begin{aligned} S_{2}=& \frac{4}{9} \pi\left(R_{3}^{2}-R_{4}^{2}\right)+4 h(r+\mathrm{d} x \tan \alpha)+\\ & \pi(r+\mathrm{d} x \tan \alpha)^{2} \end{aligned} $ | (4) |
B-B截面的周长为
| $ l=\frac{8}{9} \pi\left(R_{1}+R_{2}\right)+4 h+2 \pi r $ | (5) |
又由图中几何关系可得
| $ \left\{\begin{array}{l} \mathrm{d} L \cdot \cos \alpha=\mathrm{d} x \\ r=r_{0}+x \tan \alpha \end{array}\right. $ | (6) |
R1、R2、R3、R4与k之间的关系为
| $ \left\{\begin{array}{l} R_{1}=k+r \\ R_{2}=k-r \\ R_{3}=R_{1}+\mathrm{d} x \tan \alpha \\ R_{4}=R_{2}-\mathrm{d} x \tan \alpha \end{array}\right. $ | (7) |
将式(2)~式(6)代入式(1)中,忽略高阶量并整理得微分平衡方程为
| $ \mathrm{d} \sigma_{x}=\frac{2\left[\tau\left(1+\tan ^{2} \alpha\right)+\left(\sigma_{r}-\sigma_{x}\right) \tan \alpha\right]\left[8 \pi k / 9+2 h+\pi\left(r_{0}+x \tan \alpha\right)\right]}{\left(r_{0}+x \tan \alpha\right)\left[16 \pi k / 9+4 h+\pi\left(r_{0}+x \tan \alpha\right)\right]} \mathrm{d} x $ | (8) |
设金属坯料与模具腔体之间的摩擦系数为μ,近似塑性条件为
| $ \sigma_{1}-\sigma_{3}=\left(-\sigma_{x}\right)-\left(-\sigma_{r}\right)=\sigma_{\mathrm{s}} $ | (9) |
将式(8)代入式(7)中,并积分得到挤压区在x轴方向的应力为
| $ \sigma_{x}=\frac{\sigma_{\mathrm{s}}\left[\mu\left(1+\tan ^{2} \alpha\right)+\tan \alpha\right]}{\tan \alpha} \times \ln \frac{\left(16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}\right)+2 \tan \alpha\left(8 k \pi / 9+2 h+\pi r_{0}\right) x+\pi \tan ^{2} \alpha x^{2}}{16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}}+C $ | (10) |
边界条件为x=0,通过主应力法计算得到定径带处的挤压应力
| $ \sigma_{\mathrm{xe}}=\frac{\mu \sigma_{\mathrm{s}}\left(16 \pi k / 9+4 h+2 \pi r_{0}\right)}{16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}} L_{\mathrm{d}} $ | (11) |
代入式(9)中得积分常数
| $ C=\frac{\mu \sigma_{\mathrm{s}}\left(16 \pi k / 9+4 h+2 \pi r_{0}\right)}{16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}} L_{\mathrm{d}} $ | (12) |
因此,U型模具型腔内的轴向应力为
| $ \sigma_{x}=\frac{\sigma_{\mathrm{s}}\left[\mu\left(1+\tan ^{2} \alpha\right)+\tan \alpha\right]}{\tan \alpha} \times \ln \frac{\left(16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}\right)+2 \tan \alpha\left(8 k \pi / 9+2 h+\pi r_{0}\right) x+\pi \tan ^{2} \alpha x^{2}}{16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}}+ \\ \frac{\mu \sigma_{\mathrm{s}}\left(16 \pi k / 9+4 h+2 \pi r_{0}\right)}{16 \pi k r_{0} / 9+4 h r_{0}+\pi r_{0}^{2}} L_{\mathrm{d}} $ | (13) |
式中:τ为剪应力, MPa; l为B截面周长, mm; α为型腔倾斜角度, (°); σs为屈服应力, MPa; μ为摩擦系数;Ld为定径带长度, mm。
初始设置参数, 屈服应力σs为80 MPa,摩擦系数μ为0.3,定径带长度Ld为15 mm,使用Matlab编程软件绘出Ⅲ区型腔压应力σx与厚度t的关系曲线,如图 13所示。
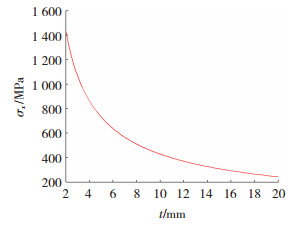
|
图 13 σx与t关系曲线 Fig.13 Relationship curve of σx and t |
当t小于4 mm时,Ⅲ区的压应力可达1 000 MPa以上,若腔体内的总压应力过大则会导致挡料块处超负荷,致使挡料块损坏,因此,通过数值模拟与解析计算可以为不同厚度铜带的生产提供理论参考。
通过有限元模拟发现,当产品厚度t发生变化,Ⅱ区扩展腔大小不变,Ⅰ区、Ⅱ区的压力总和p12变化不大;若产品宽度b改变时,Ⅱ区扩展腔大小也需随之变化。Ⅰ、Ⅱ两区腔体形状相较Ⅲ区更为简单,有限元法与解析法计算结果相差不大,因此,通过有限元分析拟合出Ⅰ区、Ⅱ区压力总和p12与产品宽度b之间的关系为
| $ p_{12}=0.0006 b^{2}-0.1214 b+161.92 $ | (14) |
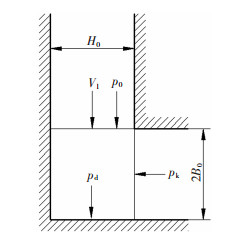
由图 14进料口处压力示意图可以推算,金属坯料流入进料口时受到的挤压应力pk表达式为
| $ p_{k}=\sigma_{x}+0.0006 b^{2}-0.1214 b+161.92 $ | (15) |
|
图 14 进料口处应力示意图 Fig.14 Schematic diagram of stress at feed inlet |
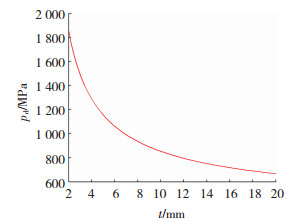
金属坯料进入挤压轮后在挡料块处流动方向产生90°改变,具有侧向挤压的特点,变形过程受到轮槽侧壁的约束,可看作平面变形问题。通过对直角挤压区的力能计算,得出进料口处压应力pk与挡料块压应力pd之间的相互关系,见式(20)。由于进料口处的压应力pk随产品厚度t的变化而变化,利用Matlab软件可作出挡料块处单位压应力pd与产品厚度t的关系曲线,如图 15所示。挤压区变形力为
| $ P_{0}=\frac{N_{\mathrm{z}}}{V_{1}} $ | (16) |
|
图 15 挡料块应力pd与t的关系曲线 Fig.15 Relationship curve of stopper block stress pd and t |
挤压区单位变形力为
| $ P_{0}=\frac{P_{0}}{H_{0} L_{0}} $ | (17) |
挡料块承受单位压应力为
| $ P_{\mathrm{d}}=p_{0}+\frac{2 k_{1} \cdot 2 B_{0} \cdot H_{0}}{L_{0} \cdot H_{0}} $ | (18) |
式中:Nz为直角弯曲区的总功率, (N·mm)/s; Vl为轮槽中坯料速度, mm/s; H0为轮槽高度, mm; L0为轮槽宽度; 进料口高度为2B0; kl为直角挤压区的剪应力, MPa; σl为直角挤压区的屈服应力,根据Mises屈服准则可得
| $ k_{1}=\frac{\sigma_{1}}{\sqrt{3}} $ | (19) |
最终得到挡料块单位压应力pd与进料口处压应力pk的关系为
| $ p_{\mathrm{d}}=p_{\mathrm{k}}+125 $ | (20) |
将TLJ630连续挤压机的各参数数据代入式(15)中,可得出图 15所示挡料块载荷pd与t的关系曲线。
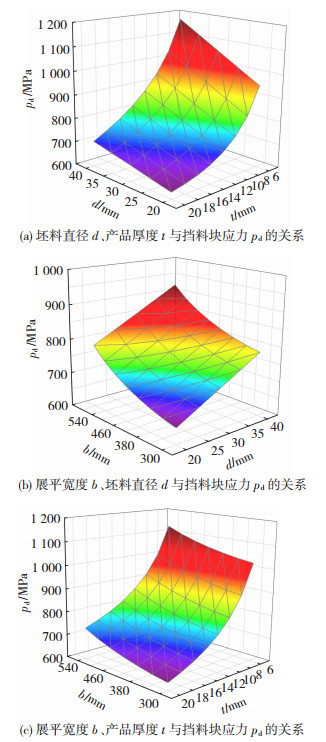
通过解析法计算结合模拟分析,得出如图 16所示的坯料直径d、产品厚度t、展平宽度b与挡料块应力pd之间的相互关系。
|
图 16 三维关系图 Fig.16 Three-dimensional relationship diagram: (a) relationship between billet diameter d, product thickness t, and stopper block stress pd; (b) relationship between flattening width b, billet diameter d, and stopper block stress pd; (c) relationship between flattening width b, product thickness t, and stopper block stress pd |
从图 16(a)可以看到,坯料直径一定时,产品厚度越小,型腔内金属的塑性变形程度越剧烈,位于挡料块上方的单位压应力越大,厚度小于8 mm时,挡料块应力可超过1 000 MPa,会对挡料块造成损坏;图 16(b)显示,展平宽度增加,挡料块应力逐渐增大,这是由于模腔内的金属克服摩擦做功增多,当展平宽度为580 mm时,挡料块应力最大可达924 MPa,仍在极限承受范围内;由图 16(c)可以得出,产品宽厚比越大,挡料块应力越大,且厚度t对挡料块应力的影响程度要大于展平宽度b,挡料块应力pd最大值可达到1 100 MPa以上。
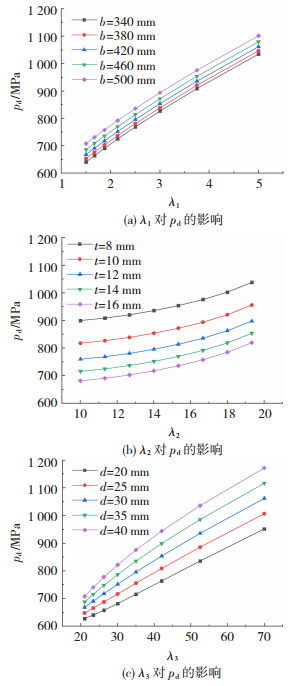
结合图 17等压力变化图进行分析,可以发现随着各参数比的增加,挡料块应力皆呈现逐渐增长的趋势,但增长幅度各不相同。
|
图 17 各参数比对pd的影响 Fig.17 Influence of different parameter ratios on pd: (a) influence of λ1 on pd; (b) influence of λ2 on pd; (c) influence of λ3 on pd |
图 17(a)显示,在宽度不变条件下,厚度挤压比λ1从1.5增加到5时,挡料块应力增长了400 MPa;λ1一定时,展平宽度b的变化对挡料块应力pd的影响程度不大,宽度340与500 mm的应力差不超过100 MPa;图 17(b)中直径扩展比λ2从10增加到16.67时,挡料块应力pd增长缓慢,λ2不变时,厚度t越小,应力增加幅度越大;图 17(c)中,随着产品宽厚比λ3的增大,坯料直径d的变化对挡料块应力的影响越来越显著,直径为20 mm与40 mm的应力差达250 MPa。
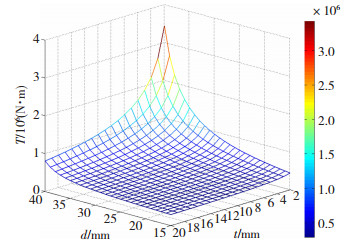
5 挤压轮扭矩计算樊志新等[17]提出了“五分区”连续挤压变形过程描述模型,五分区和挡料块示意图如图 18和图 19所示。本文通过此模型计算出连续挤压机工作过程中总扭矩T与坯料直径d和产品厚度t的关系,如图 20所示。

|
图 19 挡料块示意图 Fig.19 Schematic diagram of stopper block |
|
图 20 总扭矩T与d和t三维关系图 Fig.20 Three-dimensional relationship diagram of total torque T, d, and t |
由于U型形状的变化会使型腔内的压应力发生改变,位于挡料块上方的高温变形区的体积也会随之变化,公式(21)表达了高温变形区体积受坯料直径d和U型厚度t的影响。从图 20可以发现,坯料直径d较大时,厚度t越小,挤压轮扭矩增长幅度越大;而坯料直径或厚度过小时,扭矩变动程度不大。由图 21可知,厚度t在合理范围内时,坯料直径d最大值约为40 mm;当坯料直径d为30 mm、展平宽度b为420 mm时,理论上可以挤压出厚度t大于2 mm的铜带。
| $ \Delta \theta_{4}=\frac{1}{l} \cdot \ln \left(\frac{p_{\mathrm{d}}-\xi \sigma_{\mathrm{sh}}}{\frac{2}{\sqrt{3}} \sigma_{\mathrm{sl}} K_{\mathrm{m}} K_{\mathrm{k}}-\xi \sigma_{\mathrm{sh}}}\right) $ | (21) |
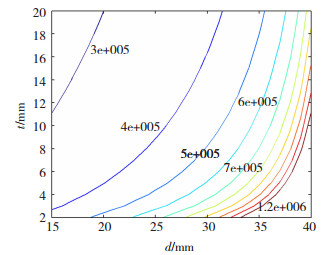
|
图 21 总转矩T与d和t的等高线图(T单位:N·m) Fig.21 Contour map of total torque T, d, and t (T unit: N·m) |
式中:
其中, Km, Kn, Kk等参数无实际意义, 均是为方便于计算。
在连续挤压生产过程中,挤压轮扭矩受到多方面因素的影响,图 22表明,随着厚度挤压比λ1、直径扩展比λ2、产品宽厚比λ3的增大,总扭矩T皆呈现出逐渐上升的趋势,但提升幅度各不相同。图 22(a)和(b)均显示出随着参数比的增大,挤压轮总扭矩逐渐增加,且厚度t对总扭矩的影响程度略大于展平宽度b,由图 22(c)可以看出,坯料直径d增大时,总扭矩T的提升幅度十分显著,最大扭矩差达1.2×106 N·m,因此,可得出对挤压轮总扭矩影响大小的主次因素是:坯料直径d >产品厚度t >展平宽度b。

|
图 22 总扭矩T随参数比的变化 Fig.22 Changes in total torque T with parameter ratios: (a) change in total torque T with λ1; (b) changes in total torque T with λ2; (c) changes in total torque T with λ3 |
本文研究的U型铜材极限尺寸主要受到连续挤压过程的制约,例如挤压机电动机的最大功率,挡料块的极限载荷。通过数值模拟与理论计算,可将流速均方差SDV、挡料块应力pd、挤压轮总扭矩T作为判定标准,综合推导出可挤压产品的极限尺寸,根据数值模拟结果与实际生产情况综合分析,SDV的极限值为10,高于此值挤压出的铜材无法加工处理;H13钢挡料块的最大载荷值为1 000 MPa,TLJ630连续挤压机的额定扭矩为9.55×105 N·m,由表 3数据分析得出,坯料直径d为30 mm、展平宽度b为420 mm时,可挤压出的极限厚度t为7 mm。
| 表 3 极限尺寸分析 Table 3 Limit size analysis |
U型铜带连续挤压实验设备选用TLJ630连续挤压机,如图 23所示。坯料采用Φ30 mm的纯铜铜杆,腔体、模具预热温度为500 ℃,挤压出的U型铜带样品如图 24所示。挤压机功率为600 kW,电机转速为600 r/min,额定电流为1 450 A,速比100,电流数据采集如图 25所示。实验中通过记录的电枢电流计算出挤压时的实际转矩,再与各理论转矩比较得到相对误差,实验测试结果如表 4所示。

|
图 23 TLJ630连续挤压机 Fig.23 TLJ630 continuous extruder |

|
图 24 14 mm的U型铜带样品 Fig.24 14 mm U-shaped copper strip sample |

|
图 25 电流数据采集 Fig.25 Current data collection |
| 表 4 实验测试数据 Table 4 Experimental data |
1) 应用HyperXtrude有限元软件对不同几何参数比的铜带产品进行连续挤压数值模拟。随着厚度挤压比λ1的增加,速度分布越来越不均匀,SDV值增幅明显;随着直径扩展比λ2的增加,SDV值变化范围不大。
2) 利用解析法建立挡料块应力pd与尺寸r0的函数模型,得到厚度挤压比λ1、直径扩展比λ2、产品宽厚比λ3对挡料块应力pd的影响规律。
3) 根据“五分区”法计算出连续挤压过程总扭矩T与坯料直径d和产品厚度t的关系,计算结果表明,坯料直径d对T的影响程度最大,根据判定标准得到,当坯料直径d为30 mm、展平宽度b为420 mm时,可挤压出U型铜带的极限尺寸厚度t为7 mm。
| [1] |
童金林. 铜及铜合金连续挤压技术的研究和应用[J]. 世界有色金属, 2019(21): 156-157. TONG Jinlin. Research and application of continuous extrusion technology of copper and copper alloys[J]. World Nonferrous Metals, 2019(21): 156-157. |
| [2] |
阮红生. 连续挤压技术在铜加工中的应用探讨[J]. 世界有色金属, 2019, 535(19): 213-215. RUAN Hongsheng. Discussion on the application of continuous extrusion technology in copper processing[J]. World Nonferrous Metals, 2019, 535(19): 213-215. DOI:10.3969/j.issn.1002-5065.2019.19.122 |
| [3] |
陈国权, 张敬恩, 骆越峰, 等. 连续挤压铜带坯缺陷的分析和解决措施[J]. 铜业工程, 2019, 4(3): 16-19. CHEN Guoquan, ZHANG Jingen, LUO Yuefeng, et al. Analysis and solution of defects in continuous extrusion of copper strip[J]. Copper Industry Engineering, 2019, 4(3): 16-19. |
| [4] |
刘元文, 闫志勇, 易飞. 金属板带坯料的连续挤压生产方法: CN201710355778.8[P]. 2017-08-11. LIU Yuanwen, YAN Zhiyong, YI Fei. Continuous extrusion production method of sheet metal blanks: CN201710355778.8[P]. 2017-08-11. |
| [5] |
YUN Xinbing, YOU Wei, ZHAO Ying, et al. Continuous extrusion and rolling forming velocity of copper strip[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(4): 1108-1113. DOI:10.1016/S1003-6326(13)62572-8 |
| [6] |
KOSHMIN A N, ZINOVIEV A V, CHASNIKOV A V, et al. Investigation of the stress-strain state and microstructure transformation of electrotechnical copper buses in the deformation zone during continuous extrusion[J]. Russian Journal of Non-Ferrous Metals, 2021, 62(2): 179-189. DOI:10.17073/0021-3438-2021-1-36-48 |
| [7] |
孙健, 刘平, 刘新宽, 等. Cu-Ni-Si合金连续挤压过程中的组织演变及性能[J]. 中国有色金属学报, 2014, 24(4): 944-949. SUN Jian, LIU Ping, LIU Xinkuan, et al. Microstructure evolution and properties of Cu-Ni-Si alloy during continuous extrusion[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(4): 944-949. DOI:10.19476/j.ysxb.1004.0609.2014.04.014 |
| [8] |
郭华仲, 宋宝韫, 陈莉. 连续挤压杆坯直径的工艺影响研究[J]. 锻压技术, 2010, 35(1): 138-141. GUO Huazhong, SONG Baoyun, CHEN Li. Study on the process influence of continuous extrusion rod blank diameter[J]. Forging & Stamping Technology, 2010, 35(1): 138-141. DOI:10.3969/j.issn.1000-3940.2010.01.037 |
| [9] |
宋宝韫, 宋娜娜, 陈莉. 宽铜母线连续挤压扩展成形挤压力的分析[J]. 塑性工程学报, 2011, 18(4): 7-10. SONG Baoyun, SONG Nana, CHEN Li. Extrusion force analysis of continuous extrusion and expansion forming of wide copper busbar[J]. Chinese Journal of Plasticity Engineering, 2011, 18(4): 7-10. DOI:10.3969/j.issn.1007-2012.2011.04.002 |
| [10] |
于孟, 代娜娜, 钟毅. 铜排连续挤压力能的工程法计算[J]. 中国机械工程, 2012, 23(21): 2630-2633. YU Meng, DAI Nana, ZHONG Yi. Calculation of continuous extrusion force and energy of copper bar by engineering method[J]. China Mechanical Engineering, 2012, 23(21): 2630-2633. DOI:10.3969/j.issn.1004-132X.2012.21.024 |
| [11] |
赵颖, 裴久杨, 郭丽丽, 等. 宽厚比对双杆连续挤压6063铝合金焊合质量的影响[J]. 材料导报, 2020, 34(24): 114-120. ZHAO Ying, PEI Jiuyang, GUO Lili, et al. The effect of width-to-thickness ratio on the welding quality of 6063 aluminum alloy by double-rod continuous extrusion[J]. Materials Review, 2020, 34(24): 114-120. DOI:10.11896/cldb.20050039 |
| [12] |
徐宁宁, 孙朝阳, 钱凌云, 等. 镁合金板形件扭-挤成形载荷的主应力法求解模型[J]. 机械工程学报, 2021, 57(4): 73-82. XU Ningning, SUN Chaoyang, QIAN Lingyun, et al. The principal stress method solution model of torsion-extrusion forming load of magnesium alloy plate parts[J]. Chinese Journal of Mechanical Engineering, 2021, 57(4): 73-82. DOI:10.3901/JME.2021.04.073 |
| [13] |
CAO Furong, WEN Jinglin, DING Hua, et al. Force analysis and experimental study of pure aluminum and Al-5%Ti-1%B alloy continuous expansion extrusion forming process[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 201-207. DOI:10.1016/S1003-6326(13)62447-4 |
| [14] |
YUN Xinbing, TIAN Tian, ZHAN Hong, et al. Microstructure evolution of copper strip during continuous extrusion and rolling forming[J]. Materials Science Forum, 2018, 4740: 277-285. DOI:10.4028/www.scientific.net/MSF.913.277 |
| [15] |
JIA Lu, LI Yongtang, Hui Tianjing, et al. Numerical simulation and experimental research on microstructural evolution during compact hot extrusion of heavy caliber thick-wall pipe[J]. Chinese Journal of Mechanical Engineering, 2019, 32(1): 113-126. DOI:10.1186/s10033-019-0316-z |
| [16] |
KUMAR SINHA Devendra, KUMAR Santosh, KUMAR Anil, et al. Mathematical modelling to predict mechanical properties of Copper (C101) feedstock in continuous extrusion[J]. IOP Conference Series: Materials Science and Engineering, 2018, 404(1): 115-120. DOI:10.1088/1757-899X/404/1/012052 |
| [17] |
樊志新, 宋宝韫, 刘元文, 等. 连续挤压变形力学模型与接触应力分布规律[J]. 中国有色金属学报, 2007, 4(2): 283-289. FAN Zhixin, SONG Baoyun, LIU Yuanwen, et al. Continuous extrusion deformation mechanics model and contact stress distribution law[J]. The Chinese Journal of Nonferrous Metals, 2007, 4(2): 283-289. DOI:10.3321/j.issn:1004-0609.2007.02.017 |
 2022, Vol. 30
2022, Vol. 30