镁合金是目前实际应用的最轻的金属,密度约为1.74 g/cm3,具有较高的比强度和比刚度,在要求轻质化的航空航天领域以及汽车领域极具前景[1-3]。由于镁合金导热性强,热膨胀系数大等特点,对焊接过程热输入十分敏感。冷金属过渡焊(CMT)的短路过渡以及焊丝回抽可有效降低热输入,是镁合金材料的有效焊接方法之一[4-7]。曲宏韬等人[8]利用CMT得到了组织性能较好的镁合金堆焊层。CMT焊缝成形的形状和尺寸受到焊丝-熔池传热流动的共同影响,因此针对这一过程建立计算流体力学(CFD)模型,对了解熔池流动传热及控制CMT焊缝成形具有重要意义。柏兴旺[9]、张天雷[10]等人建立了等离子弧焊以及MIG焊电弧增材制造数值模型,预测了沉积金属层的尺寸及熔池流动趋势。饶政华[11]、曾承宗[12]及王岑[13]等人同样以建立数值模型的方式研究了CMT焊接的传热传质过程,得到了金属蒸汽在CMT电弧等离子体中的扩散特点以及温度场对于液态金属润湿行为的影响。本文旨在研究CMT堆焊中焊丝抽送对熔池传热传质过程以及焊缝成形的影响,建立CMT多相流数值模型,并加入自动响应的焊丝抽送运动,以更准确的模拟CMT熔池动态行为。
1 建立CMT堆焊数值模型 1.1 模型描述及简化CMT堆焊是多物理场耦合的复杂过程,首先送丝阶段电弧燃起,加热基板金属并使焊丝端部熔化形成熔滴,送丝至熔滴接触熔池后发生短路进入回抽阶段,此时电弧熄灭,热输入与电流密度大幅降低,并瞬间改变焊丝运动方向进行回抽,完成短路过渡如图 1所示。熔池在不同阶段的受力情况如图 2所示,当熔滴与熔池发生接触时,熔池受到的电弧作用力随电弧熄灭而消失。

|
图 1 CMT堆焊过程示意图 Fig.1 Schematic diagram of CMT welding process: (a) wire feeding process; (b) wire redrawing process |

|
图 2 CMT堆焊不同阶段的熔池受力情况 Fig.2 Force of molten pool during different stages in CMT welding: (a) wire feeding stage; (b) wire redrawing stage |
为得到合理结果且降低计算成本,本模型做出如下假设:
1) 忽略镁合金相变的组分输运过程;
2) 热导率等热物性参数仅与温度相关;
3) 电磁场分布由经验公式给出;
4) 电弧对熔池的作用力、热输入以源项代替;
5) 熔滴的最高温度为定值。
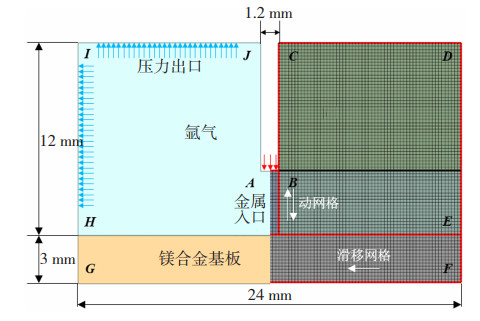
1.2 网格划分及动网格控制建立二维几何模型如图 3所示,EFGH区域为镁合金基板,区域DEHI在初始时刻充满氩气,液态镁合金在速度入口AB流入,边界HI、IJ、CD、DE视为压力出口不限制流体流动,边界EF、GH仅有基板内部热传导,为绝热边界条件,基板底部GF与周围环境发生对流换热与辐射。其中EFGH区域为滑移网格来模拟基板与焊丝之间的相对运动,DEHI区域为动网格生成区域来模拟焊丝抽送的上下运动。
|
图 3 几何模型及网格划分 Fig.3 Geometric model and meshing |
对几何模型进行网格划分,为保证较高的网格质量并防止动网格出现负体积,全部采用网格尺寸为边长0.1 mm的四边形结构化网格,单元数量为35 040,节点数量为35 752。
整个计算域均视为流体,基于有限体积法对N-S方程组进行离散求解,使用流体体积法(VOF)追踪自由表面,控制方程组如下:
连续性方程
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho v)=0 $ | (1) |
动量守恒方程
| $ \begin{gathered} \frac{\partial(\rho v)}{\partial t}+\nabla \cdot(\rho v v)=-\nabla p+\nabla \cdot[\mu(\nabla v)]+ \\ \rho g+F_{\mathrm{pla}}+F_{\mathrm{ap}}+F_{\mathrm{as}}+F_{\mathrm{mag}}+F_{\mathrm{b}}+ \\ F_{\mathrm{s}}+F_{\mathrm{ma}}+F_{\mathrm{ms}} \end{gathered} $ | (2) |
能量守恒方程
| $ \frac{\partial}{\partial t}(\rho h)+\nabla \cdot(v \rho h)=\nabla \cdot(k \nabla T)+S_{\text {arc }}+S_{\text {loss }} $ | (3) |
VOF体积分数方程
| $ \frac{\partial \alpha_q}{\partial t}+(\nabla \cdot v) \alpha_q=0 $ | (4) |
式(2)右边第三项到第十项为动量源项;第四项是等离子流拉力Fpla, 仅作用于熔滴区域;第五项、第六项分别是电弧压力Fap和电弧剪切力Fas和仅作用于熔池区域;第七项到第十一项分别是电磁力Fmag、浮力Fb、表面张力Fs、马兰戈尼力Fma和固-液区阻力Fms,同时作用于熔滴和熔池两个区域。
式(3)右边第二项、第三项为能量源项,表示计算域内的体积热源。其中Sarc是作用于熔池表面的电弧热输入,Sloss是基板表面的对流换热及辐射造成的能量损失。在熔滴与熔池接触的短路阶段,式(2)、(3)中等离子流拉力项、电弧压力项、电弧剪切力项、电磁力项,以及电弧热输入项均降为零。
式(4)中αq代表第q相体积分数,其范围在0到1之间。
1.3 源项处理 1.3.1 熔滴熔池区域划分控制焊丝的抽送丝转换需要判断熔滴、熔池两个区域的接触,且熔滴和熔池的动量源项以及能量源项需要区分。首先遍历中线上所有单元并判断αmetal变量(图 4红色区域),若遍历完成后满足αmetal小于0.5的单元数量不为零,则熔滴与熔池尚未接触,反之则已接触,并在遍历完成后可得到熔滴长度H、熔池高度h以及弧长L,如图 4(a)。

|
图 4 熔滴与熔池区域划分 Fig.4 Division of droplet and pool regions: (a) no contact between droplet and pool; (b) droplet in contact with pool |
当焊丝抽送过程中出现气泡时,若仅遍历中线上的单个区域,即使熔滴与熔池已经接触,但由于气泡的存在,仍会得出尚未接触的结果,将无法正确判断其接触状态。为了避免这种情况,采用分别遍历中线周围多个区域的方法,令其只要有一个区域的遍历结果为已接触,则判断为已接触,即可避免气泡对于接触判断的影响,如图 5所示。

|
图 5 存在气泡时的判断方法 Fig.5 Determination method in the presence of droplet: (a) traverse of a single region; (b) traverse of multiple regions |
等离子流拉力是熔滴在电弧等离子体流的作用下受到的向下的拉力,其大小为
| $ F_{\text {pla }}=C_{\mathrm{D}} \pi\left(R_{\mathrm{d}}^2-R_{\mathrm{w}}^2\right) \frac{\rho v^2}{2} $ | (5) |
式中:CD为等离子流系数;Rd为熔滴等效半径;Rw为熔滴颈缩部位半径;ρ为等离子流的密度;v为等离子流速度[14]。
电弧压力Fap表示为以焊丝轴线为中心的高斯分布,电弧剪切力Fas表示为距离焊丝轴线1 mm处为中心的高斯分布,可用下式表达:
| $ F_{\text {ap }}=P_{\max } \exp \left(-\frac{r^2}{2 \sigma_{\mathrm{q}}^2}\right) $ | (6) |
| $ \left\{\begin{array}{l} x>0, F_{\mathrm{as}}=\tau_{\max } \exp \left(-\frac{(r-0.001)^2}{2 \sigma_{\mathrm{q}}^2}\right) \\ x<0, F_{\mathrm{as}}=\tau_{\max } \exp \left(-\frac{(r+0.001)^2}{2 \sigma_{\mathrm{q}}^2}\right) \end{array}\right. $ | (7) |
式中Pmax、τmax为最大电弧力和最大电弧剪切力,根据电流和保护气密度得出[15],分别取421和80 N。
电磁力Fmag为电流密度与磁场强度矢量的叉乘,可由下式获得
| $ F_{\text {mag }}=J \times B $ | (8) |
其中电流密度以及磁场强度在熔滴熔池中的分布表示为式(9)至式(11):
| $ J_z=\frac{k I y}{2 \pi H} \exp \left(-k x^2\right)+\frac{I}{2 \pi R_w^2}\left(1-\frac{y}{H}\right) $ | (9) |
| $ J_r=\frac{1}{2 \pi x H}\left[1-\exp \left(-k x^2\right)-\frac{k x}{2 \pi H}\right] $ | (10) |
| $ B_{\rm{ \mathsf{ θ}}}=\frac{\mu_0 I y}{2 \pi x H}\left[1-\exp \left(-k x^2\right)\right]+\frac{\mu_0 k x I}{4 \pi}\left(1-\frac{y}{H}\right) $ | (11) |
式中:k为电流集中系数; x为距离焊丝中心线的径向距离; y为距离焊丝端部的轴向距离; H为熔滴长度[16]。
密度变化产生的浮力Fb用Boussinesq假设来考虑,可由式(12)计算
| $ F_{\mathrm{b}}=\rho \beta g\left(T-T_1\right) $ | (12) |
CMT堆焊过程存在因温度梯度产生的表面张力梯度,马兰戈尼力表示为表面张力梯度与切向温度梯度的乘积,表面张力Fs与马兰戈尼力Fma的表达式为:
| $ F_{\mathrm{s}}=\sigma \nabla \cdot \frac{\nabla \alpha}{|\nabla \alpha|} $ | (13) |
| $ F_{\mathrm{ma}}=\frac{\mathrm{d} s}{\mathrm{~d} T} \cdot \frac{\partial T}{\partial s} $ | (14) |
式中σ为表面张力系数。
镁合金的熔化凝固由焓-孔隙度法模拟,将镁合金相全部视为流体,但温度低于液相线以下的区域会受到固液区阻力,表达为式(15)
| $ F_{\mathrm{ms}}=\frac{(1-\varphi)^2}{\left(\varphi^3+\varepsilon\right)} A_{\mathrm{mush}} v $ | (15) |
式中:φ为液相体积分数;ε和Amush为常数。
利用连续表面力(CSF)方法[17]将动量源项中电弧压力、电弧剪切力、表面张力和马兰戈尼力等表面力转换为加载于相界面网格上的体积力,如式(16)所示。
| $ F_{\text {body }}=F_{\text {surface }} \frac{\rho \nabla \alpha_{\text {metal }}}{\frac{1}{2}\left(\rho_{\text {metal }}+\rho_{\text {gas }}\right)} $ | (16) |
式中:▽αmetal为体积分数梯度;ρ为气相和镁合金相体积分数平均密度。
1.3.3 能量源项由于熔池表面受到电弧的能量输入,以高斯分布的形式表示其热流密度,如式(17),且在镁合金基板与氩气的界面处存在对流和辐射,相应的热损失表达为式(18)。
| $ q_{\text {arc }}(r)=\frac{\eta U I}{2 \pi \sigma_{\mathrm{q}}^2} \exp \left(-\frac{r^2}{2 \sigma_{\mathrm{q}}^2}\right) $ | (17) |
| $ q_{\text {loss }}=-\varepsilon k_{\mathrm{B}}\left(T^4-T_{\text {amb }}^4\right)-h_{\mathrm{c}}\left(T-T_{\mathrm{amb}}\right) $ | (18) |
式中:σq为高斯热流分布参数;η为焊接热效率;r为距离热源中心的距离;ε为表面辐射系数;kB为斯蒂芬-玻尔兹曼常数;Tamb为环境温度;hc为综合对流换热系数。其中σq,η随弧长L的改变而改变,近似呈线性反比关系[18]。
根据熔滴熔池接触状态的判断,电弧热输入在熔滴尚未接触熔池的电弧阶段生效,在熔滴接触熔池后的短路阶段自动降至零,以体现CMT热输入的脉冲性质。
以类似连续表面力的方法将热流密度转化为自由表面上的体热源,获得热流密度表达式
| $ S_{\text {arc/loss }}=q_{\text {arc/loss }} \frac{\rho\left|\nabla \alpha_{\text {metal }}\right|}{\frac{1}{2}\left(\rho_{\text {metal }}+\rho_{\text {gas }}\right)} $ | (19) |
每个时间步开始计算之前对熔滴熔池区域是否接触进行判断,若熔滴接触熔池,令焊丝继续向下送进0.6 mm后开始回抽,检测到焊丝脱离熔池继续向上回抽1.8 mm后再次变为送丝运动,完成一个CMT熔滴过渡周期,动网格变化过程如图 6所示。

|
图 6 焊丝动网格示意图 Fig.6 Schematic diagram of dynamic grids |
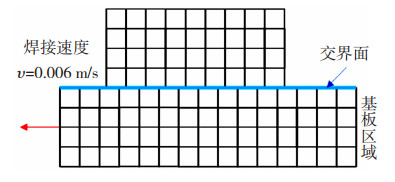
基板区域的滑移速度等于焊接速度,为0.006 m/s,如图 7所示。
|
图 7 基板滑移网格示意图 Fig.7 Schematic diagram of substrate slip grids |
使用高速摄像观测直径1.2 mm的AZ31B镁合金焊丝在69 A焊接电流下的CMT堆焊过程,送丝运动速度0.3 m/s,抽丝运动速度0.9 m/s。
1.4.2 边界条件速度入口处流入镁合金的速度等于镁合金的熔化速度,送丝阶段镁合金焊丝受热熔化的体积等于脱离焊丝时的熔滴体积,可表达为
| $ v_{\text {melt }}=\frac{4 R^3}{3 r^2 t} $ | (20) |
式中:R为熔滴半径;r为焊丝半径;t为送丝持续时间。高速摄像实验中测得某一周期中送丝持续时间0.012 s,熔滴半径0.000 6 m,求得熔化速度约为0.06 m/s。
熔滴过渡过程中热输入非常低,温度边界降为905 K,熔化速度降为0.01 m/s。基板底部的对流换热及辐射可表达为
| $ -\frac{\partial T}{\partial n}=-\varepsilon k_{\mathrm{B}}\left(T^4-T_{\mathrm{amb}}^4\right)-h_{\mathrm{c}}\left(T-T_{\mathrm{amb}}\right) $ | (21) |
模型边界条件如表 1所示,AZ31B镁合金及氩气热物性参数如表 2,其中高温区间的参数通过插值法以及外推法获得。
| 表 1 边界条件 Table 1 Boundary conditions |
| 表 2 材料热物性参数 Table 2 Thermal property parameters of materials |
采用焊接电流69 A,焊接电压12 V,焊接速度6 mm/s的工艺参数,AZ31B镁合金焊丝直径为1.2 mm,利用基于压力的SIMPLE瞬态求解方法,时间步长取3×10-5 s,对镁合金CMT堆焊数值模型进行前10个CMT周期的计算。
在相同参数下进行镁合金CMT堆焊实验并使用高速摄像记录堆焊金属与焊丝的动态行为,其中第1、2、3、10个熔滴过渡周期与数值模拟结果对比如图 8所示,可见自响应焊丝抽送模型对于熔池动态行为的模拟结果与高速摄像的实验结果具有良好吻合。结果显示在前10个周期内,镁合金熔滴在送丝阶段均无自主脱落,主要原因是CMT较低的功率下,电磁力、重力等不足以形成颈缩促进熔滴的脱离。当熔滴接触熔池并继续达到最大送进距离时,焊丝立即回抽,此阶段在CMT周期中的功率达到最低,热输入大幅降低,熔滴依靠机械回抽主动脱离焊丝,以相对较低的温度进入熔池,完成平稳的短路过渡,并且在模拟结果与实验结果中均未出现飞溅,与MIG焊的滴状过渡相比,短路过渡显著减少了镁合金堆焊过程的飞溅。液态镁合金动力粘度较低,仅为液态低碳钢的三分之一到四分之一,熔池内流体的剪切应力较其他焊接金属更小,有更强的流动性,故高速的抽送丝对熔池造成了强烈的搅动,导致熔池表面产生较大变形,且焊丝回抽时,由于气液界面存在表面张力,在焊丝端部与熔池之间的液态金属产生液桥,熔池被拉高,使最终形成高宽比偏大、接触角偏大的焊缝。
在激光焊等深熔焊中,形成熔池匙孔或指状熔深,能量密度高度集中,蒸发面积小,蒸发反力对熔池流动有显著影响[21],但CMT堆焊热输入较小且造成的熔深较浅,故在本模型中忽略相变引起的蒸发反力,不影响模拟结果的准确性与合理性。

|
图 8 镁合金CMT堆焊动态过程数值模拟结果与实验结果对比 Fig.8 Comparison between numerical simulation and experimental results of CMT dynamic surfacing process of magnesium alloy: (a) the first droplet transition period; (b) the second droplet transition period; (c) the third droplet transition period; (d) the tenth droplet transition period |
在前3个熔滴过渡周期中,沉积在基板上的镁合金体积与质量较小,此时CMT的抽送丝使液态镁合金的表面有较大波动; 在第4个周期至第10个周期,熔滴相对于已沉积的镁合金质量较小,不足以使液态镁合金的表面产生较大变化,逐渐进入稳定堆焊过程。
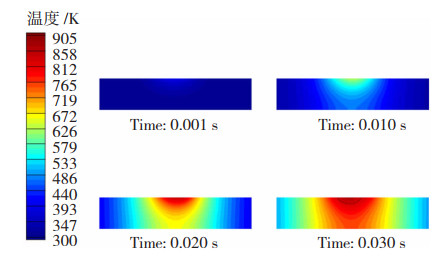
2.2 温度场流场分布及熔池形态将除基板之外的其他区域忽略,仅观察镁合金基板的温度场分布规律以及变化过程,在堆焊初始时刻基板温度场分布变化如图 9所示。在0.001 s时刚刚起弧,电弧开始对基板产生加热作用,但由于此时加热时间非常短,基板温度尚未有明显变化;在0.01 s时,此时基板受到电弧加热作用开始升温,热量由上表面传入基板,由于热传导作用,热量在基板内部开始迅速扩散,开始呈现圆弧状的等温线,此时基板最高温度已被迅速加热到600 K;在0.02 s时,基板已有明显温升,温度已经接近镁合金液相线,且可以看到在电弧加热、基板内部的热传导、以及基板外表面与空气的对流散热条件下,热量主要聚集在电弧加热位置,在基板下表面的中心位置,等温线呈现漏斗状,这是由于在中心处受到热量最多,且沿中心线向下的方向离基板下表面最近,是最快的散热路径;在0.03 s时,此时第1个CMT周期的熔滴过渡已经完成,基板上出现固液相分界线,开始熔化形成熔池。可见在堆焊起始阶段,基板温度迅速升高,直到第一次熔滴过渡后,基板被加热熔化产生熔池。
|
图 9 堆焊初期基板温度场变化 Fig.9 Variation of temperature field of substrate at the beginning of surfacing |
经历3个CMT周期后,基板温度分布特点以及变化情况如图 10所示。在0.075 s时,在基板内部已经有很明显的热量累积,电弧作用区周边5 mm的区域均达到719 K温度以上,且在远离电弧作用区的位置,温度向基板两侧均匀扩散,等温线接近竖直,可见0.95 s到0.135 s时间内基板温度场分布无明显变化。

|
图 10 3个熔滴过渡周期后基板温度场变化 Fig.10 Variation of temperature field of substrate after three droplet transition periods |
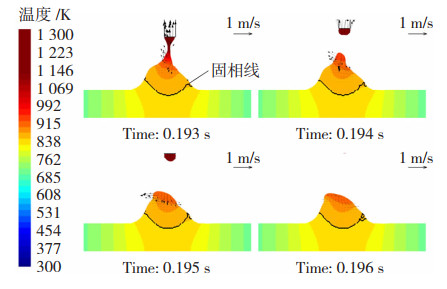
以第9个熔滴过渡周期为例,焊丝回抽之后熔池的表面变化,温度场、流场分布,以及固相线的位置如图 11所示。在焊丝回抽作用下,熔滴离开焊丝时处于被拉长状态,受到表面张力影响,熔滴有使各处表面张力平衡的趋势,在熔池中铺展并对熔池造成冲击,在熔滴冲击,电弧力以及马兰戈尼力的共同作用下,液态镁合金向熔池后方快速流动,随后从熔池后方流回熔池前方。受熔滴携带热量以及电弧热输入的作用,熔池中心位置温度最高,热量通过热传导向基板底部以及基板两侧扩散。在焊丝回抽过程中,熔池在机械回抽的作用下被拉高,使传至基板的热量更少,导致在此工艺条件下会形成熔深较浅、且余高较高的焊缝。
|
图 11 焊丝回抽时温度场和流场变化 Fig.11 Variation of temperature field and flow field while wire redrawing |
相同周期内的熔池形态变化如图 12所示,堆焊过程焊丝与熔池之间有焊接方向的相对速度,熔池沿焊接方向的前方受热密度高于后方,导致熔池出现后拖现象,呈现前方深后方浅的形态。

|
图 12 焊丝回抽时的熔池形态 Fig.12 Molten pool shape during wire redrawing |
每一个CMT周期熔滴过渡阶段结束后的沉积金属形貌以及熔池形态如图 13所示,沉积金属尺寸逐步增大,且熔池形态保持稳定,熔池尺寸在热积累作用下不断扩大。

|
图 13 每个周期熔滴过渡后的熔池形态 Fig.13 Pool morphology after droplet transition in each period |
相同工艺参数下的镁合金CMT焊缝成形如图 14(a),制备焊缝横截面金相试样,经磨抛腐蚀后观察到清晰的熔合线如图 14(b),测得焊缝熔深为0.549 mm。

|
图 14 镁合金焊缝熔深 Fig.14 Welding pool depth of magnesium alloy: (a) weld appearance; (b) weld cross section |
CMT堆焊模型的数值模拟结果中,熔深达到了0.53 mm,堆焊过程第0.054 s的熔深示意如图 15所示,与所选横截面金相图中的实际熔深0.549 mm之间存在3.47%的误差,这是由于模型中的镁合金热物性参数与材料的实际属性存在误差,以及CMT堆焊过程中存在飞溅等不稳定性因素。

|
图 15 数值模拟熔深预测结果 Fig.15 Numerical simulation results of depth prediction |
1) 通过遍历单元并读取单元内VOF变量进行逻辑判断的方式,实现在多相流模型中准确判断熔滴熔池之间的接触状态及其区域划分,将熔滴熔池接触状态与焊丝动网格模型相关联,在CMT堆焊模型中实现了以短路检测控制的焊丝自动抽送,可准确模拟焊丝抽送对熔池动态行为的影响,焊丝回抽与马兰戈尼力为熔池动态行为的主导作用力。
2) 本模型对镁合金CMT堆焊的熔深进行了预测,熔深深度0.53 mm,与实际成形焊缝的熔深之间具有良好吻合性,验证了模型准确性。
| [1] |
丁文江, 吴国华, 李中权, 等. 轻质高性能镁合金开发及其在航天航空领域的应用[J]. 上海航天, 2019, 36(2): 5-12. DING Wenjiang, WU Guohua, LI Zhongquan, et al. Development of lightweight and high performance magnesium alloys and their applications in aerospace field[J]. Aerospace Shanghai, 2019, 36(2): 5-12. DOI:10.19328/j.cnki.1006-1630.2019.02.001 |
| [2] |
XU Tiancai, YANG Yan, PENG Xiaodong, et al. Overview of advancement and development trend on magnesium alloy[J]. Journal of Magnesium and Alloys, 2019, 7(3): 536-544. DOI:10.1016/j.jma.2019.08.001 |
| [3] |
曹东东, 梅瑞斌, 包立, 等. AZ31B镁合金带材热轧过程组织均匀性及性能研究[J]. 材料科学与工艺, 2020, 28(4): 41-47. CAO Dongdong, MEI Ruibin, BAO Li, et al. Study on the microstructure and properties of AZ31B magnesium alloy strip in hot rolling[J]. Materials Science and Technology, 2020, 28(4): 41-47. DOI:10.11951/j.issn.1005-0299.20190023 |
| [4] |
张洪涛, 冯吉才, 胡乐亮. CMT能量输入特点与熔滴过渡行为[J]. 材料科学与工艺, 2012, 20(2): 128-132, 139. ZHANG Hongtao, FENG Jicai, HU Leliang. Energy input and metal transfer behavior of CMT welding process[J]. Materials Science and Technology, 2012, 20(2): 128-132, 139. DOI:10.11951/j.issn.1005-0299.20120224 |
| [5] |
RAKSHITH M, SEENUVASAPERUMAL P. Review on the effect of different processing techniques on the microstructure and mechanical behaviour of AZ31 Magnesium alloy[J]. Journal of Magnesium and Alloys, 2021, 9(5): 1692-1714. DOI:10.1016/j.jma.2021.03.019 |
| [6] |
ZHANG Heng, HU Shengsun, WANG Zhijiang, et al. The effect of welding speed on microstructures of cold metal transfer deposited AZ31 magnesium alloy clad[J]. Materials & Design, 2015, 86(5): 894-901. DOI:10.1016/j.matdes.2015.07.143 |
| [7] |
张文毓. 堆焊技术的研究与应用进展[J]. 现代焊接, 2014(12): 21-25. ZHANG Wenliu. Research and application progress of surfacing welding technology[J]. Modern Welding Tec-hnology, 2014(12): 21-25. |
| [8] |
曲宏韬, 申俊琦, 步贤政, 等. AZ31镁合金CMT堆焊工艺与接头组织研究[J]. 航天制造技术, 2017, 2(1): 34-37. QU Hongtao, SHEN Junqi, BU Xianzheng, et al. Study on CMT surfacing technology and microstructure of AZ31 magnesium alloy[J]. Aerospace Manufacturing Technology, 2017, 2(1): 34-37. DOI:10.3969/j.issn.1674-5108.2017.01.009 |
| [9] |
BAI Xingwang, COLEGROVE P, DING Jialuo, et al. Numerical analysis of heat transfer and fluid flow in multilayer deposition of PAW-based wire and arc additive manufacturing[J]. International Journal of Heat and Mass Transfer, 2018, 124: 504-516. DOI:10.1016/j.ijheatmasstransfer.2018.03.085 |
| [10] |
张天雷, 徐刚, 沈艳涛, 等. 基于MIG的电弧增材制造熔池行为的数值模拟[J]. 智能计算机与应用, 2020, 10(5): 261-266. ZHANG Tianlei, XU Gang, SHEN Yantao, et al. Numerical simulation of molten pool behavior in arc additive manufacturing based on MIG[J]. Intelligent Computer and Applications, 2020, 10(5): 261-266. |
| [11] |
饶政华, 李芸霄, 刘江维, 等. 铝合金与镀锌钢板CMT焊接过程传热传质现象的数值模拟[J]. 中南大学学报(自然科学版), 2015, 46(11): 4325-4333. RAO Zhenghua, LI Yunxiao, LIU Jiangwei, et al. Numerical simulation of heat and mass transfer between aluminum alloy and galvanized steel plate during CMT welding[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4325-4333. DOI:10.11817/j.issn.1672-7207.2015.11.046 |
| [12] |
曾承宗, 林巧力, 曹睿, 等. 冷金属过渡下熔融铝合金在钢板上润湿铺展的数值模拟[J]. 焊接学报, 2017, 38(3): 57-61, 131. ZENG Chengzong, LIN Qiaoli, CAO Rui, et al. Simulation of spreading of molten Al alloy on Q235 steel under the cold metal transfer condition[J]. Transactions of The China Welding Institution, 2017, 38(3): 57-61, 131. |
| [13] |
王岑, 曹睿, 林巧力, 等. 镁/钛异种金属冷金属过渡焊接的温度场模拟[J]. 焊接学报, 2015, 36(4): 17-20, 114. WANG Cen, CAO Rui, LIN Qiaoli, et al. Numerical simulation on temperature distribution of cold metal transfer joining magnesium to titanium dissimilar metals[J]. Transactions of The China Welding Institution, 2015, 36(4): 17-20, 114. |
| [14] |
FAN H G, KOVACEVIC R. Droplet formation, detachment, and impingement on the molten pool in gas metal arc welding[J]. Metallurgical and Materials Transactions B, 1999, 30(4): 791-801. DOI:10.1007/s11663-999-0041-6 |
| [15] |
CAMPBELL S W, GALLOWAY A M, MCPHERSON N A. Arc pressure and fluid flow during alternating shielding gases.Part 2: arc force determination[J]. Science and Technology of Welding and Joining, 2013, 18(7): 597-602. DOI:10.1179/1362171813y.0000000141 |
| [16] |
陈茂爱, 武传松, 廉荣. GMAW焊接熔滴过渡动态过程的数值分析[J]. 金属学报, 2004, 40(11): 1227-1232. CHEN Maoai, WU Chuansong, LIAN Rong. Numerical analysis of GMAW welding droplet transition dynamic process[J]. Acta Metallurgica Sinica, 2004, 40(11): 1227-1232. DOI:10.3321/j.issn:0412-1961.2004.11.020 |
| [17] |
BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y |
| [18] |
TSAI N S, EAGAR T W. Distribution of the heat and current fluxes in gas tungsten arcs[J]. Metallurgical Transactions B, 1985, 16: 841-846. DOI:10.1007/BF02667521 |
| [19] |
丁文江. 镁合金科学与技术[M]. 科学出版社, 2007.
|
| [20] |
付瑜, 韩绍华, 薛丁琪. 基于金属蒸汽和外加磁场的MIG电弧模拟[J]. 兵器材料科学与工程, 2021, 44(3): 94-98. FU Yu, HAN Shaohua, XUE Dingqi. MIG arc simulation based on metal vapor and applied magnetic field[J]. Ordnance Material Science and Engineering, 2021, 44(3): 94-98. DOI:10.14024/j.cnki.1004244x.20210330.001 |
| [21] |
刘秀航, 高向东, 孙友松, 等. 激光-电弧复合焊接技术研究现状[J/OL]. 热加工工艺, 2022, 51(7): 7-11. LIU Xiuhang, GAO Xiangdong, SUN Yousong, et al. Research status of laser-arc composite welding technology[J/OL]. Hot Working Technology, 2022, 51(7): 7-11. DOI: 10.14158/j.cnki.1001-3814.20201690 |
 2022, Vol. 30
2022, Vol. 30


