2. 利多合金有限公司, 江苏 常州 213125
2. Changzhou Liduo Alloy Co., Ltd., Changzhou 213125, China
柔性接触式应变传感器[1-2]在智能机器人、可穿戴电子器件、人机交互界面、生物医疗传感器以及人体健康监测等高新科技领域具有十分广泛的工程应用。柔性应变传感器的创新开发在近十年中获得了研究者极大的关注,并取得了迅速的发展。研究中最先采用的是导电纳米复合材料薄膜[3-4]或“纳米颗粒导电层与聚合物”双层薄膜[5-8]。Heng等[7]采用银镜制备法在聚二甲基硅氧烷(Polydimethylsiloxane,PDMS)上合成了纳米银颗粒薄膜,其灵敏度(仪器灵敏度Gauge Factor,以下简称GF)峰值可达75(ε≤5%),且在1 Hz的频率下表现出良好的线性。Hu等[8]采用改进的化学镀方法,在PDMS上制备了金属银包覆聚苯乙烯球(PS@Ag)薄膜,该薄膜具有良好的应变传感性能。Kim等[4]采用旋涂法制备了AgNWs(银纳米线)/PDMS弹性导电复合材料薄膜,在100%的应变下该薄膜具有可靠的可逆传感能力、高灵敏度(GF=32)、高线性度(R2>0.996)和低滞回响应(DH < 12%)。上述材料薄膜(无结构的均匀薄膜)的传感特性完全取决于材料自身性能,在大应变下材料薄膜的压阻(电阻随应变的变化)测量范围,稳定性,滞回性和线性度通常会变差[5-8],导致无法满足实际工程应用的需求。
为了打破柔性传感器对传感材料的完全依赖,研究人员以结构薄膜代替原有的材料薄膜,希望通过结构的设计获得超越材料本身的传感特性。目前采用的结构有褶皱结构[9]、螺旋结构[10]、金字塔结构[11]、多孔结构[1]和剪纸结构[12-13]等。其中剪纸结构被广泛应用。Xu等[12]采用激光直写聚酰亚胺薄膜的方法制备剪纸结构石墨烯-聚合物复合薄膜,结构的引入使得薄膜具有高拉伸性(应变>200%)和高灵敏度(应变60%时电阻变化>80%)。
受国内外同行前期工作的启发,为进一步发掘新颖结构,深入探讨结构、制备工艺与薄膜传感特性的关系,获得优化的结构薄膜设计,本文对菱形剪纸结构柔性传感薄膜进行了全面的研究。首先通过激光切割得到了菱形PDMS薄膜,然后采用银镜制备法合成了纳米银颗粒/聚二甲基硅氧烷(AgNPs/PDMS)结构薄膜。随后采用模拟与实验结合的方法研究了制备工艺、菱形结构参数与压阻性能的关系。该工作的成果将为柔性传感薄膜的发展及其在电子皮肤和可穿戴电子设备等方面的工程应用提供有益的指导。
1 有限元模拟高弹性材料的应力-应变关系是强非线性的,因此其本构关系常以弹性势能与应变关系表征,即弹性势能函数。该函数是应变张量的标量函数,其对应变分量的导数是对应的应力分量[14]。聚二甲基硅氧烷(PDMS)是一种典型的高弹性材料,其拉伸极限可达800%[15]。
常见的高弹性材料本构关系模型有Neo-Hookean模型、Yeoh模型[16-17]、Mooney-Rivlin模型等[18]。Yeoh模型只依赖于第一个应变常数I1,通过简单拉伸试验获得的该参数值可以适用于各种不同的复杂变形方式。此外,Yeoh模型描述的变形范围也较宽,适合于大变形下力学行为的模拟。因此,本文采用了Yeoh模型模拟PDMS材料。Yeoh模型的应变能密度函数为[16-17]
| $ W=\sum\limits_{i=1}^N\left(I_1-3\right)^i+\sum\limits_{k=1}^N \frac{1}{d_k}(J-1)^{2 k} $ | (1) |
式中:J为变形后与变形前的体积比;dk(k = 1, 2, 3,…,N)为材料常数,其中N为正整数;I1=λ12+λ22+λ32为变形张量不变量,λ1,λ2和λ3为主伸长比,即拉伸后试样长度与初始试样长度的比值。
Yeoh模型的三项参数形式为
| $ W=C_{10}\left(I_1-3\right)+C_{20}\left(I_1-3\right)^2+C_{30}\left(I_1-3\right)^3 $ | (2) |
式中:λ1,λ2和λ3可通过拉伸实验所确定,即λ1=εx,λ2=εy,λ3=εz=0;材料参数C10,C20和C30则通过拉伸实验数据与模拟软件(ANSYS,workbench 16.0) 的拟合来确定。
为验证模型的可靠性,我们对长方形PDMS薄膜(几何尺寸为:长度70 mm,宽度25 mm,厚度0.3 mm)进行单轴拉伸,所得应力-应变曲线和实验结果在图 1中进行了对比。如图 1所示,模拟与实验结果基本一致,说明Yeoh模型可以较好地表征PDMS本构关系,描述PDMS薄膜的力学行为。

|
图 1 PDMS薄膜拉伸实验与模拟对比 Fig.1 Comparison between tensile test and simulation on PDMS film |
PDMS薄膜,厚度0.3 mm,购买于杭州包尔得新材料科技有限公司。硝酸银(AgNO3,99.8%,分析纯)、无水葡萄糖(C6H12O6,99%,生物技术级)、氨水(NH5O,质量分数25%~28%,分析纯)、盐酸多巴胺(C8H11NO2·HCl,98%,化学纯)、三羟甲基氨基甲烷(Tris,99.9%,生物技术级)、盐酸(HCl,35% ~38%,分析纯)、乙醇(C2H6O,99.7%,化学纯),均购买自上海麦克林生化科技有限公司。
2.2 仪器与设备超声清洗仪:型号SB-3200DTD,宁波新芝生物科技股份有限公司;数显恒温磁力搅拌器:型号MS-H550-Pro,苏州科瑞斯仪器有限公司;电子天平:型号DV215CD,奥豪斯仪器(上海)有限公司;万用拉伸机:型号HS-3000A,上海和晟仪器有限公司;数字万用表:型号Keithley-2100,泰克科技有限公司;真空干燥箱:型号SG-ZKX250,中国科学院上海光学精密机械研究所;激光切割机:型号CW-650R,苏州创轩激光科技有限公司。
2.3 结构薄膜的制备 2.3.1 制备工艺本研究在结构薄膜的基础上制备了AgNP传感结构薄膜,具体制备工艺如下:
菱形PDMS薄膜的制备:将结构图纸导入激光切割机上,设置激光参数:最大功率4 W,最小功率3.5 W,切割速度11 mm/s,在平台上放置好完整的PDMS薄膜(长×宽:70 mm×25 mm) 进行切割。激光切割部位为薄膜中间30 mm×25 mm,两边各预留20 mm×25 mm(夹具部位尺寸)。
配置100 mL浓度为10 mmol/L的Tris溶液。在60 ℃恒定温度下,向Tris中滴入少量HCl调整其pH值至8.5,制成Tris-HCl缓冲液[19]。称取200 mg盐酸多巴胺粉末溶解于上述缓冲液并搅拌3 min,制得多巴胺溶液。保持溶液60 ℃恒温待用。
传感薄膜的制备:将菱形PDMS基底样品(3片)依次经过乙醇溶液和纯水超声清洗5 min后,浸入多巴胺溶液中。浸泡12~24 h后,将样品取出,用大量纯水冲洗,并置于真空干燥箱内室温干燥。
2.3.2 AgNPs的生长彻底清洗用于制备银氨溶液的玻璃器皿并烘干。量取40 mL(0.2 mmol/L) 硝酸银溶液。将体积分数为2%的氨水逐滴滴入硝酸银溶液并不断搅拌,直至最初生成的沉淀刚好溶解为止。
将银氨溶液与50 mL(0.5 mmol/L) 葡萄糖溶液混合,搅拌10 s形成均匀混合溶液。将经过预处理的聚合物基底样品浸入混合溶液中,分别静置12、23 min后取出,即获得PDMS基底上的AgNPs导电薄膜。扫描电镜图及能谱图如图 2、图 3。图 2中可见球状及棒状的银颗粒,这与王成原等前期的观测[6-7]及文献中的报道[20-21]基本一致。

|
图 2 银颗粒层SEM图 Fig.2 SEM image of AgNP layer |
|
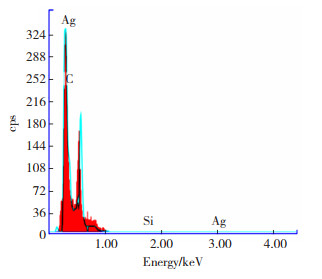
图 3 银颗粒层能谱图 Fig.3 EDAX spectrum of AgNP layer |
图 3的能谱图进一步证实了表面层的高银含量。银镜制备法中银颗粒大小、分布及均匀性,银颗粒层与聚合物基底结合状态及上述特性与薄膜传感特性关系的讨论见文献[6-7],本文主要探讨薄膜结构及尺寸与传感特性的关系。
2.3.3 样品测试与表征双层结构薄膜表面电阻通过数字万用表测量;结构薄膜的拉伸性能使用万用拉伸机测试,拉伸速率50 mm/min(以300%为最大应变,加载一次)。
3 结果与讨论 3.1 应变比测试在本节中通过有限元软件(ANSYS)模拟单轴拉伸试验,测试菱形薄膜整体与局部的应变比γ。该参数反映了局部材料实际应变与薄膜整体应变的差异,因此能准确地描述应变传感薄膜的力学特性,对无结构的PDMS材料薄膜而言γ≈1。
如图 4所示,L为菱形长度,a为菱形宽,x为菱形边缘厚度(平行于拉伸方向),y为节点长度(垂直于拉伸方向)。为探讨结构参数与力学特性γ的关系,考虑了几组不同的菱形结构参数,如表 1、表 2所示。表 1里x=y=0.1 mm不变,改变L和a;表 2里L=5 mm,a=0.02 mm不变,改变x和y。

|
图 4 菱形结构示意图 Fig.4 Schematic diagram of diamond structure |
| 表 1 菱形剪纸结构尺寸L,a参数 Table 1 Size parameters(L and a)of diamond kirigami structure |
| 表 2 菱形剪纸结构尺寸x,y参数 Table 2 Size parameters(x and y)of diamond kirigami structure |
图 5表示了菱形结构薄膜应变比γ随结构参数L、a、x和y量值的变化。结果显示应变比γ基本不随应变而改变,其量值主要取决于菱形结构的几何尺寸。

|
图 5 应变比-应变关系随L,a(a)和x,y(b)的变化 Fig.5 Variation of strain ratio-strain relation with L and a(a) and x and y(b) |
图 5(a)可见γ随L的增大而快速增大,但随a的增大而逐渐减小,例如给定a=0.02 mm下,当L从1 mm增大7倍到7 mm时,应变比γ从27.66提升至345.74,增大了约12.5倍。给定L=5 mm下,a从0.02 mm增大25倍到0.5 mm时,应变比从233.94减小到60.08,减小了74%。因此,增大菱形长度L,减小其宽度a可以有效提升该剪纸薄膜的应变比γ。这里L/a可以成为另一个表征量,γ将随该比值的增大而提高。进一步观察图 5(b)可发现当菱形长度和宽度固定时,应变比γ随x,y的减小而增大,且x对应变比γ的影响要比y大40倍,例如,当L=5 mm,a=0.02 mm,y=0.1 mm而x从0.5 mm减少到0.1 mm时,应变比从4.31增大到233.94,增大了约54.24倍;给定L=5 mm,a=0.02 mm,x=0.1 mm,当y从0.5 mm减少到0.1 mm时,应变比γ从172增大到234,增大了约1.36倍。由此可见,γ对L和x最为敏感,这两个几何参量的变化能有效提升应变比。综合考虑上述模拟结果,表 1和2中给出的菱形结构参数中取L最长,a最小且边缘x宽度及节点y宽度最小的结构将给出最大的应变比γ,相应菱形剪纸结构参数为:L=7 mm,a=0.02 mm,x=y=0.1 mm。受限于本实验所使用的激光切割设备精度,本文参数设置均不小于0.5 mm。但本小节给出的最佳的切割工艺参数对于结构薄膜的设计仍具有实际的指导意义。
3.2 压阻性能测试本小节将进一步研究结构参数对菱形PDMS薄膜压阻性能的影响。首先在薄膜试样表面镀上银颗粒(AgNP),形成AgNP/PDMS双层菱形结构薄膜,如图 6所示。然后对薄膜进行单轴拉伸试验,测试不同应变下电阻变化率ΔR/R0,即
| $ \frac{\Delta R}{R_0}=\frac{R_i-R_0}{R_0} $ | (3) |

|
图 6 菱形剪纸薄膜试样几何示意图 Fig.6 Schematic diagram of diamond kirigamifilm sample |
式中:R0为初始电阻;Ri为瞬时电阻。
将x,y设定在最小值0.5 mm,a固定为1.2 mm,本小节重点考察菱形长度L和镀银沉积时间t对压阻特性的影响,试样的编号方法为L-菱形长度-t-银颗粒沉积时间,如L-7-t-23为菱形长度7 mm,镀银沉积时间23 min的菱形结构薄膜试样。
3.2.1 静载压阻范围图 7为菱形结构薄膜单轴拉伸载荷下的压阻特性,即“ΔR/R0-应变”关系。实验中考虑了4个不同的试样L-5-t-12,L-5-t-23,L-7-t-12及L-7-t-23。从图 7中可见,ΔR/R0随应变的增大而逐渐提高,当应变值达到某一临界值εcr时,ΔR/R0突然快速增大;应变超过εcr后,电阻呈指数增加且超过量程,此时薄膜上的银纳米颗粒层断裂不能导电,薄膜将不能正常工作。因此εcr表征了结构薄膜的最大应变传感量程。图 7中结果显示,当L从5 mm增大到7 mm时,薄膜最大工作范围从170%提高到250%,增大了1.47倍,因此,L的增大能明显地增加εcr。与此相反,沉积时间t的增加将降低薄膜的工作范围εcr,但t的影响比L小的多。

|
图 7 不同L, t的薄膜电阻变化与应变关系 Fig.7 ΔR/R0 and strain relation of films with different L and t |
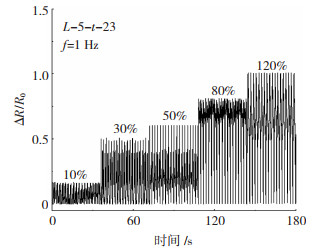
为探讨结构薄膜的动态压阻特性,将AgNP/PDMS结构薄膜进行循环拉伸实验,其最小应变为0,最大应变分别为10%、30%、50%、80%及120%,动载荷频率为1 Hz。实验中,在每个最大应变值下,动载荷循环18次。图 8记录了L-5-t-23试样“循环加载-卸载”过程中相对电阻的变化ΔR/R0。
|
图 8 周期性载荷下ΔR/R0-时间关系曲线 Fig.8 ΔR/R0-time curve under cyclic load |
图 8描述了ΔR/R0随时间的变化关系。从图中可以观察到,对于给定的最大应变,ΔR/R0的峰值在循环载荷下几乎保持恒定,不随时间或循环次数的增加而改变。这显示了结构薄膜在动载荷下出色的稳定性。当循环载荷的最大应变不断上升时,ΔR/R0最大值随之单调增加,最大应变ε与最大ΔR/R0之间具有近似线性的关系
| $ \Delta R / R_0 \propto 1.26 \varepsilon $ | (4) |
这一结果表明,在高达120%的大应变动载荷下,菱形剪纸结构薄膜表现出很高的稳定性,线性度及其灵敏度GF=1.26。2019年,Xu等[12]制备了石墨烯/聚酰亚胺矩形剪纸结构薄膜,在最大应变60%时,其传感灵敏度约为1.33。在此之前Heng等[7]制备了AgNP/PDMS材料薄膜,其最大应变仅为5%。本文制备的菱形结构薄膜与矩形结构薄膜[12]相比,在相近压阻灵敏度下,可以成倍地提升传感的最大测量范围。与材料薄膜[7]相比则可以数量级地提升其工作应变范围。这里值得提出的是,在反复加载过程中(200多次)没有发现表面层脱落现象,薄膜结构完好。在所用的传感材料中,薄膜和基体之间的变形是协调一致的,当变形产生时,银颗粒导电层产生裂纹,裂纹的长度会随应变的增大而增大,数量也会增多,这样极大地降低了两层间的应力,保证导电薄膜不会快速脱落。当外载荷去除后,弹性PDMS层收缩回复,银颗粒导电层裂纹闭合,恢复原有导电率。因此,应变传感材料可以被反复使用,不至于在早期失效。
3.2.3 压阻线性度及灵敏度进一步考察结构参数及镀银时间与其压阻线性度及灵敏度的关系。图 9描述了在循环拉伸频率为1 Hz下,不同L下菱形薄膜的ΔR/R0与最大应变ε之间的关系。

|
图 9 t=12 min (a)和t=23 min (b)时的ΔR/R0-应变图 Fig.9 ΔR/R0 strain curves under t=12 min (a) and t=23 min(b) |
其中,图 9(a)是沉积时间t为12 min的结果,图 9(b)的沉积时间t为23 min。图中各离散点为实验数据,实线是根据数据点线性拟合而成。从图 9可以观察到,在不同的L下,电阻的相对变化ΔR/R0几乎都随着最大应变的增长而线性增加。在沉积时间t为12 min时,L从3 mm增加到5 mm,线性度R2从0.902 09增加到0.998 49。当L进一步提高到7 mm时,线性度略有下降,下降为0.998 37。图 9(b)中表现出完全相同的趋势。与此同时,图 9的结果显示银颗粒的沉积时间对动载荷下的压阻线性度影响趋势不明显。
图 10给出了不同镀银时间下薄膜灵敏度与应变的关系,由图 10(a)可以发现,镀银时间为12 min时,当L由7 mm减小到5和3 mm时,灵敏度(GF=ΔR/R0ε))逐渐由0.78增加到1.51和6.03。这与应变比γ随L的变化相反,即当薄膜整体应变一定,而L增长时,局部或者材料的实际应变逐渐减小,灵敏度降低。当t为23 min时,图 10(b)显示出相似的GF-应变关系。当L由7 mm降低到5、3 mm时,GF由1.31增加到1.58、4.46,相比t=12 min时,L为7 mm时提高了68%,5 mm时提高了5%,3 mm时降低了26%。

|
图 10 t=12 min (a)和t=23 min (b)时的GF-应变图 Fig.10 GF-strain curves under t= 12 min (a) and t=23 min(b) |
以聚合物为基底的柔性应变传感材料,存在滞后或是响应延迟的现象。除聚合物基底本身的粘弹性性质之外,导电填料的粘弹性特征,纳米填料与聚合物界面间的相互作用力等因素也会导致滞后行为。这里压阻滞回率DH是表征纳米复合材料薄膜传感稳定性的重要参数,可由加-卸载全过程中材料的电阻相对变化量(ΔR/R0)与应变ε的关系曲线(即压阻滞回曲线)来定义,即
| $ \mathrm{DH}=\frac{A_{\mathrm{S}}-A_{\mathrm{R}}}{A_{\mathrm{S}}} \times 100 \% $ | (5) |
其中AS和AR分别为ΔR/R0-ε曲线中加载和卸载状态曲线下的面积。
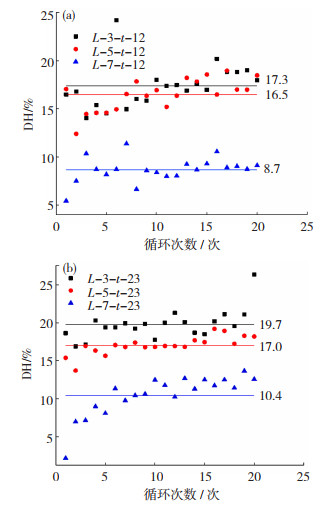
测试了AgNP/PDMS菱形结构薄膜在20次循环加载下的压阻滞回曲线。图 11给出了不同镀银时间下获得的“DH-循环次数”关系曲线。这里各离散点代表各试样每次循环的滞回率,实线则为不同L值对应滞回率DH的平均值。
|
图 11 t=12 min (a)和t=23 min (b)下的DH-循环次数图 Fig.11 DH-cycle number curves under t=12 min (a) and t=23 min(b) |
由图 11可知,在给定应变ε和沉积时间t下,DH值随L增大而减小。在最大应变为60%(图 11 (a)),t为12 min时,在菱形长度L从3 mm增大到5和7 mm的过程中,DH平均值从17.3减小16.5,再进一步减小到8.7,DH平均值最终减小了约50%。如前所述,随着L增大,其整体应变与局部应变比值γ变大,即同样整体变形下,材料的实际变形变小,这是DH值随L增大而减小,压阻稳定性提高的原因。t=23 min (图 11 (b))时,DH值随L的变化趋势以及DH平均值的变化量与t=12 min时很接近。但从另一方面看,在给定应变和L下,DH平均值随沉积时间t的增大而明显提高,例如,在最大应变为60%,L为3、5和7 mm时,如果沉积时间t从12 min增大到23 min,DH平均值分别从17.3,16.5和8.7增大到19.7,17和10.4,平均增大约12%。3.3菱形剪纸结构薄膜的应用
本文通过实例检测了菱形剪纸结构薄膜在人体运动监测中的适用性和其应变传感的各项性能。实验选择的菱形结构薄膜制备的沉积时间为12 min,其几何形状与尺寸如图 12(a)所示:试样为17 mm×60 mm的长方形,菱形结构中L=7 mm,a=1.2 mm,x=y=0.5 mm。图 12(b)为菱形结构薄膜实物图,这里电极材料为导电铜胶。将所制备的菱形剪纸结构薄膜分别固定在人体上对手指、手腕、屈膝弯曲以及下蹲动作进行监测。在反复弯曲关节时,通过数字万用表检测传感薄膜的电阻变化。

|
图 12 菱形剪纸结构薄膜几何示意图(a)和实物图(b) Fig.12 Geometric diagram (a)and physical image (b)of diamond kirigami film |
手指弯曲和手腕弯曲时“ΔR/R0-时间”关系如图 13(a)和(b)所示,图中每个上下周期代表一次完整的弯曲到放松的过程。可见,传感薄膜压阻特性较稳定,手指和手腕弯曲达到最大位移时,ΔR/R0基本稳定在一个常数值。由于最大位移及最大应变的不同,手指弯曲产生的最大ΔR/R0的平均值约为4.3,而手腕弯曲对应的平均值约为3.3。这一结果与文献[8]中的结果相近,表明本文中的结构传感薄膜与文献的灵敏度基本相同。

|
图 13 ΔR/R0与时间的关系:(a)手指弯曲;(b)手腕弯曲;(c)行走;(d)蹲起 Fig.13 Relation between ΔR/R0 and time: (a) finger bending; (b) wrist bending; (c) walking; (d) squatting |
行走及下蹲时膝盖弯曲如图 13(c)和(d)所示。膝盖运动时,信号的均匀性比较好,表明传感器具有良好的稳定性。行走时ΔR/R0最大值的平均值约为0.8,而下蹲时ΔR/R0最大值的平均值可达1左右。这比手指及手腕弯曲产生的对应值(3.3至4.3)要小很多,反映出不同部位运动时产生的位移大小不同。同时,图 13中电阻变化频率的不同也反映出身体各部位运动速度的快慢。
基于上述分析,ΔR/R0峰值的平均值及频率范围可以用于区别不同身体部位的弯曲运动。由此可见,该菱形剪纸结构薄膜能准确检测并追踪人体动作的信号,且根据电阻变化的特定范围和特定谱图区别动作部位、幅度及频率。这表明所获得的结构薄膜能够达到传感设备的基本要求,适用于监测不同部位的人体运动,在电子皮肤和可穿戴电子设备中具有广阔的应用前景。
4 结论1) 菱形剪纸结构设计的应变比提升两个数量级以上,工作范围扩大了近50倍。大应变比保证了大变形下结构薄膜较好的线性度、稳定性以及适当的灵敏度。菱形结构应变比随L,x和y的增大而增大,随a的增大而逐渐减小;其中应变比对L和x最为敏感。
2) 菱形结构几何参量L和薄膜合成工艺参数t对薄膜的压阻传感性能(工作范围,线性度,滞回率,灵敏度)均可产生影响。L的增大能显著的增大薄膜的工作范围和线性度同时降低薄膜的滞回率,但L的增加,亦会降低薄膜的灵敏度。t对工作范围,线性度和灵敏度影响较小,但会增加滞回率。
3) 本文制备的传感薄膜(尺寸为L=7 mm,a=1.2 mm,x=y=0.5 mm)在100%的大变形下具有良好的线性度和稳定性,以及合理的灵敏度。在灵敏度相近的情况下,其工作范围大于矩形结构薄膜。
4) 制备的菱形剪纸结构薄膜能准确检测并追踪人体动作的信号,且根据电阻变化的特定范围和特定谱图区别动作部位、幅度及频率。
| [1] |
SUN Xuguang, SUN Jianhai, LI Tong, et al. Flexible tactile electronic skin sensor with 3D force detection based on porous CNTs/PDMS nanocomposites[J]. Nano-Micro Letters, 2019, 11(1): 57. DOI:10.1007/s40820-019-0288-7 |
| [2] |
KUMAR K S, CHEN P Y, REN H. A review of printable flexible and stretchable tactile sensors[J]. AAAS Research, 2019, 2019(1): 3018568. DOI:10.34133/2019/3018568 |
| [3] |
MJADI M, PICHITPAJONGKIT A, LEE S, et al. Highly stretchable and sensitive strain sensor based on silver nanowire-elastomer nanocomposite[J]. ACS Nano, 2014, 8(5): 5154-5163. DOI:10.1021/nn501204t |
| [4] |
KIM H J, THUKRAL A, YU C. Highly sensitive and very stretchable strain sensor based on a rubbery semiconductor[J]. ACS Applied Materials & Interfaces, 2018, 10(5): 5000-5006. DOI:10.1021/acsami.7b17709 |
| [5] |
赵越, 俞笑竹, 张康, 等. 柔弹性复合薄膜的制备及其力电性能测试[J]. 材料科学与工程学报, 2020, 38(3): 414-419. ZHAO Yue, YU Xiaozhu, ZHANG Kang, et al. Fabri-cation and mechanical/electrical property testing of el-astomeric composite films[J]. Journal of Materials Science & Engineering, 2020, 38(3): 414-419. DOI:10.14136/j.cnki.issn1673-2812202003012 |
| [6] |
张康, 俞笑竹, 王成原, 等. 纳米银-聚合物薄膜的制备及力电性能测试[J]. 材料科学与工艺, 2020, 28(6): 11-28. ZHANG Kang, YU Xiaozhu, WANG Chengyuan, et al. Preparation of silver-polymer film and its mechanical and properties characterizationg[J]. Materials Science and Technology, 2020, 28(6): 11-28. DOI:10.11951/j.issn.1005-0299.20190003 |
| [7] |
HENG Shan, LIU Hongguang, WANG Chenyuan, et al. Electrical percolation and dynamic piezoresistivity of silver nanoparticle/polydimethylsiloxane films[J]. Materials Research Express, 2020, 7(4): 045701. DOI:10.1088/2053-1591/ab89d9 |
| [8] |
HU Yougen, ZHAO Tao, ZHU Pengli. A lowcost, printable, and stretchable strain sensor based on highly conductive elastic composites with tunable sensitivity for human motion monitoring[J]. Nano Research, 2018, 11(4): 1938-1955. DOI:10.1007/s12274-017-1811-0 |
| [9] |
MU Jiuke, WANG Gang, YAN Hongping, et al. Molecular-channel driven actuator with considerations for multiple configurations and color switching[J]. Nature Communications, 2018, 9(1): 590. DOI:10.1038/s41467-018-03032-2 |
| [10] |
ROJAS J P, AREVALO A, FOULDS I G, et al. Design and characterization of ultra-stretchable monolithic silicon fabric[J]. Applied Physics Letters, 2014, 105(15): 154101. DOI:10.1063/1.4898128 |
| [11] |
CAO Yudong, LI Tie, GU Yang, et al. Fingerprint inspired flexible tactile sensor for accurately discerning surface texture[J]. Small, 2018, 14(16): 1703902. DOI:10.1002/smll.201703902 |
| [12] |
XU Kaichen, LU Yuyao, HONDA S, et al. Highly stable kirigami-structured stretchable strain sensors for perdurable wearable electronics[J]. Journal of Materials Chemistry C, 2019, 7(31): 9609-9617. DOI:10.1039/c9tc01874c |
| [13] |
WANG Zhihui, ZHANG Ling, DUAN Shasha, et al. Kirigami-patterned highly stretchable conductors from flexible carbon nanotube-embedded polymer films[J]. Journal of Materials Chemistry C, 2017, 5(34): 8714-8722. DOI:10.1039/c7tc01727h |
| [14] |
张洪才. ANSYS 14.0理论解析与工程应用实例[M]. 机械工业出版社, 2013.
|
| [15] |
李正伟. 柔性电子多层封装及粘弹性效应分析[D]. 杭州: 浙江大学, 2012. LI Zhengwei. Multilayer packing of flexible electronics and analysis of viscoelastic effect[D]. Hangzhou: Zhejiang University, 2012. |
| [16] |
YEOH O H. Characterization of elastic properties of carbonblackfilled rubber vulcanizates[J]. Rubber Chemistry Technology, 1990, 63(5): 792-805. DOI:10.5254/1.3538289 |
| [17] |
YEOH O H. Some forms of the strain energy function for rubber[J]. Rubber Chemistry Technology, 1993, 66(5): 754-771. DOI:10.5254/1.3538343 |
| [18] |
陈莲, 周海亭. 计算橡胶隔振器静态特性的数值分析方法[J]. 振动与冲击, 2005, 24(3): 120-123. CHEN Lian, ZHOU Haiting. Numerical methods for analysing static characteristics of rubber isolator[J]. Journal of Vibration and Shock, 2005, 24(3): 120-123. DOI:10.13465/j.cnki.jvs.2005.03.035 |
| [19] |
SURESHKUMAR M, LEE P N, LEE C K. Stepwise assembly of multimetallic nanoparticles via self-polymerized polydopamine[J]. Journal of Materials Chemistry C, 2011, 21(33): 12316-12320. DOI:10.1039/C1JM11914A |
| [20] |
AHLBERG S, ANTONOPULOS A, DIENDORF J, et al. PVP coated, negatively charged silver nanoparticles: a multicenter study of their physicochemical characteristics, cell culture and in vivo experiments[J]. Beilstein Journal of Nanotechnology, 2014, 5(1): 1944-1965. DOI:10.3762/bjnano.5.205 |
| [21] |
FAHMY H M, MOSLEH A M, ELGHANY A, et al. Coated silver nanoparticles: synthesis, cytotoxicity, and optical properties[J]. RSC Advances, 2019, 9(35): 20118-20136. DOI:10.1039/c9ra02907a |
 2023, Vol. 31
2023, Vol. 31


