2. 工程机械智能制造安徽省教育厅重点实验室,合肥 230601
2. Anhui Key Laboratory of Intelligent Manufacturing of Construction Machinery, Hefei 230601, China
金属磁记忆检测是一种利用铁磁构件的磁记忆效应对其损伤状态(如应力集中)进行表征及评估的无损检测技术[1]。作为一种典型的弱磁检测方法,磁记忆检测对材料应力集中较为敏感,便于实现多通道自动化检测,常被用于构件的早期损伤评估[2-3]。目前,铁磁构件磁记忆信号检测过程常受到外磁场干扰[4],影响了检测结果的一致性。研究不同外磁场环境下铁磁构件损伤过程磁记忆信号特征及其规律,对于提高损伤评估精度,降低评估不确定性意义重大。
在金属构件损伤的磁记忆检测方面,Dubov于20世纪90年代后期率先提出了基于铁磁材料力-磁偶合效应的金属磁记忆诊断技术[5]。为实现铁磁构件应力集中及损伤的量化描述,人们在磁场强度和梯度[6]的基础上,选取模糊熵[7]、二维谱熵[8]、小波能量谱[9]等工具进行构件损伤过程的磁特征提取,结合试样初始磁化状态[10]、温度场[11]等条件,获取构件损伤过程中磁特征变化规律。在损伤模型构建方面,国内外学者提出了基于Chaboche理论的蠕变-疲劳损伤本构模型[12]、磁热弹塑性耦合模型[13]和力磁耦合[14]等模型,并将其应用于疲劳损伤评估。上述研究工作为开展铁磁构件损伤过程的磁特征提取及损伤状态评估提供了模型支撑。然而,在铁磁构件磁记忆检测工程实践中,外磁场环境对磁特征影响及外加磁场强度大小对疲劳损伤过程磁记忆信号测量值的作用机制尚不明确,增加了疲劳损伤量化评估难度。
本文选取45钢开展低周疲劳实验,获取不同外加磁场环境下(地磁场、200、400、600 A/m)试样各疲劳损伤状态的磁记忆信号。分析不同磁场环境下磁记忆信号的变化规律,提取了磁场强度法向分量Hp(y)极差值Hp(y)Rv和磁场强度梯度K最大值Kmax。基于上述特征,构建了考虑外加磁场环境的疲劳损伤模型。
1 实验 1.1 实验材料本文以同一批次45钢试样作为实验对象,试样尺寸见图 1,加工方式为激光切割。材料成分如表 1所示。

|
图 1 试样尺寸(单位:mm) Fig.1 Specimen size |
| 表 1 45钢试样成分(质量分数/%) Table 1 Chemical composition of 45 steel (wt. %) |
图 2所示为外加磁场环境低周疲劳实验装置图。

|
图 2 外加磁场环境的低周疲劳实验装置图 Fig.2 Diagram of low cycle fatigue test device under external magnetic field |
选取电液伺服疲劳试验机(SDS-200,中机试验装备股份有限公司)开展疲劳实验,设备最大负荷为±200 kN,最大位移为±75 mm。采用自制螺线管形成外加磁场环境,螺线管直径43 mm,长116 mm,漆包线直径1 mm,匝数100匝,采用直流稳压电源进行单路输出,螺线管上方接电源正极,下方接电源负极,其内部形成竖直向下的外加磁场。由于北半球地磁场方向斜向下,其竖直向下的分量磁场强度值为40 A/m,实验中外加磁场环境为实际测量值(含地磁场竖直向下分量)。
实验前,利用退磁器(TC-1,上海景欣机床附件有限公司)对试样进行退磁处理,使其初始磁状态保持基本一致,经退磁后4根试样Hp(y)值范围分别为-85~85 A/m、-48~82 A/m、-47~ 82 A/m、-64~45 A/m。将试样装夹在试验机上的自制螺线管内,在常温常压下采用恒幅值控制方式对试样进行加载,疲劳载荷为正弦波,加载幅值为0.7 mm,加载频率为5 Hz。分别在地磁场(40 A/m)、200、400和600 A/m的磁场环境下进行疲劳实验,利用金属磁记忆检测仪(EMS2000+,厦门爱德森)在卸载条件下离线测量疲劳循环周次1 000、2 000、3 000、4 000和断裂后的磁记忆信号(磁场强度法向分量Hp(y)和磁场强度梯度K值)。采集路径为图 1中的ab线段。
2 结果与分析 2.1 疲劳损伤过程磁记忆信号变化规律图 3所示为沿试样检测路径ab获取的外加磁场作用下疲劳损伤过程磁场强度法向分量Hp(y)的变化曲线。试样在循环载荷下发生塑性形变,材料内部孔洞、夹杂等不连续区域会产生应力的不均匀分布,出现应力集中现象。图中可见,各疲劳损伤状态(循环次数)对应的Hp(y)值均存在过零点,过零点处对应试样应力集中等隐性损伤区域。除初始和断裂阶段外,试样各数据采集点(不含过零点)对应的Hp(y)绝对值均随循环周次的增加而增加。表 2为外加磁场作用下的试样表面磁场强度法向分量最大值Hp(y)max和最小值绝对值|Hp(y)min |,可见,Hp(y)max和|Hp(y)min|随着循环周次的增加逐渐增大。试样断裂后,Hp(y)max和|Hp(y)min|达到最大,磁场强度值明显增加,这与材料位错密度及钉扎能变化有关,在断口附近磁信号发生了反向形成正负磁极,出现“磁反转”现象。各外加磁场作用下磁记忆信号变化规律相似。

|
图 3 不同外加磁场下疲劳损伤过程Hp(y)曲线 Fig.3 Hp(y) curve of fatigue damage process under different external magnetic fields: (a) geomagnetic field; (b) 200 A/m; (c) 400 A/m; (d) 600 A/m |
| 表 2 外加磁场作用下的Hp(y)max和|Hp(y)min| Table 2 Hp(y)max and |Hp(y)min| under external magnetic fields |
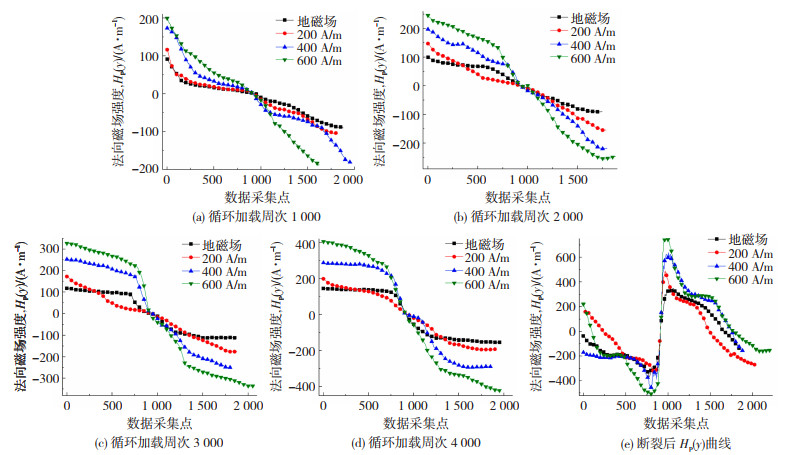
图 4所示为不同循环次数时外加磁场作用下对应的Hp(y)变化曲线。由图 4和表 2可见相同疲劳循环周次下,随着外加磁场强度的增大,Hp(y)max和|Hp(y)min|值均逐渐增加。
|
图 4 不同循环次数时外加磁场作用下的Hp(y)曲线 Fig.4 Hp(y) curve under external magnetic field at different cycle times: (a) 1 000 loading cycles; (b) 2 000 loading cycles; (c) 3 000 loading cycles; (d) 4 000 loading cycles; (e) Hp(y) curve after fracture |
图 5为不同外加磁场下疲劳损伤过程磁场强度梯度K的变化曲线,右侧坐标轴对应断裂阶段数值。图中可见随着损伤程度的增大,在Hp(y)过零点处K值呈上升趋势,断裂后K值达到最大,最大值随着外加磁场强度的增加而增加。不同外加磁场下相同循环次数对应的K值无显著变化规律。

|
图 5 不同外加磁场下疲劳损伤过程K曲线: (a) 地磁场; (b) 200 A/m; (c) 400 A/m; (d) 600 A/m Fig.5 K curve of fatigue damage process under different applied magnetic fields: (a) geomagnetic field; (b) 200 A/m; (c) 400 A/m; (d) 600 A/m |
为了对试样疲劳损伤程度进行量化评估,须在获取的磁记忆信号基础上进一步提取磁特征量。本文在磁记忆信号分析基础上,提取了磁场强度法向分量Hp(y)极差值Hp(y)Rv,Hp(y)Rv=Hp(y)max-Hp(y)min,其中Hp(y)max为对应于某一疲劳损伤阶段的Hp(y)曲线最大值,Hp(y)min为最小值。此外在K值曲线基础上提取了磁场强度梯度最大值Kmax,Kmax为对应于某一疲劳损伤阶段K值最大值。
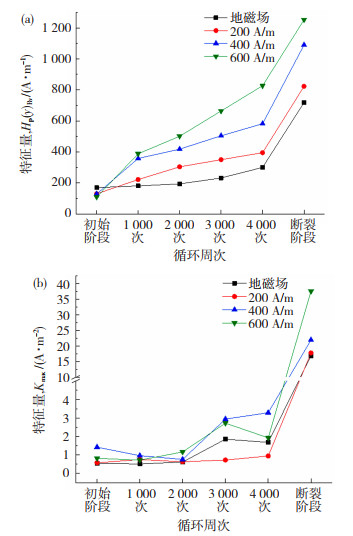
图 6为不同外加磁场下疲劳过程磁信号特征量变化曲线。
|
图 6 不同外加磁场下疲劳损伤过程特征量Hp(y)Rv (a)和Kmax(b)曲线 Fig.6 Curves of characteristic parameters Hp(y)Rv (a) and Kmax(b) of fatigue damage process under different applied magnetic fields |
由图 6可见当外加磁场方向与地磁场一致时,在一定外加磁场范围内,外加磁场会对磁记忆信号起强化作用,表现为:随外加磁场的增大,对应于各疲劳损伤阶段(循环周次)的Hp(y)Rv值逐渐增大,且Hp(y)Rv随循环周次的增加而增加。此外,对应于疲劳断裂阶段的Kmax值随着外加磁场的增大逐渐增大,且随循环周次的增加,Kmax值在疲劳断裂阶段显著增大,其他各损伤阶段无明显变化规律。外磁场对磁信号的强化机制可以从磁畴体积变化、磁畴壁聚合以及磁畴转动角度进行描述[15]。外加磁场会使铁磁材料系统总能增加,其内部磁畴体积与方向会发生改变以抵消系统增加的静磁能和弹性能。与外加磁场方向一致的磁畴体积变大,与其相反的磁畴体积变小,距离较近的磁畴壁相互靠拢,磁畴朝着外磁场方向发生转动。当外磁场消失后,铁磁体被磁化,宏观表现为磁记忆信号增强。
3 基于磁记忆信号特征量Hp(y)Rv和Kmax的疲劳损伤模型构建 3.1 基于经典连续损伤力学的低周疲劳损伤模型低周疲劳损伤主要是由于循环塑性应变累积所造成[16]。根据连续损伤力学理论,采用α来描述损伤累积程度,可得到损伤模型[17]
| $ D=1-\left(1-D_0\right)\left(1-N / N_{\mathrm{f}}\right)^{\alpha_{N_{\mathrm{f}}}} $ | (1) |
式中:D0为初始损伤;D为损伤参量;N为循环周次;Nf为疲劳寿命。模型中指数αNf与材料性能和实验环境有关,尚无统一表达式。本文实验仅改变磁场环境,为明确外加磁场大小与损伤参量之间的关系,可采用与外加磁场大小有关的函数表达式Ψ(ΔH)替换αNf以描述损伤累积的程度。假设每一次的循环造成的损伤量相同,得到疲劳损伤模型如下
| $ D = 1 - \left( {1 - {D_0}} \right){\left( {1 - N/{N_{\rm{f}}}} \right)^{\mathit{\Psi }(\Delta H)}} $ | (2) |
为构建基于Hp(y)Rv和Kmax的疲劳损伤模型,以磁记忆信号特征量Hp(y)Rv和Kmax表征材料损伤参量D,如式(3)、(4)所示:
| $ D = 1 - {H_{\rm{p}}}{(y)_{{\rm{Rv}}0}}/{H_{\rm{p}}}{(y)_{{\rm{Rv}}N}} $ | (3) |
| $ D=1-K_{\max 0} / K_{\max N} $ | (4) |
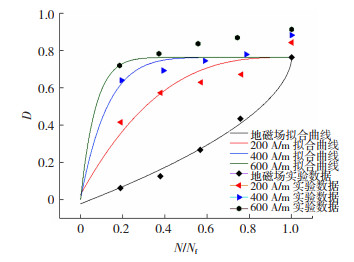
式中:Hp(y)Rv0和Kmax0为初始无损伤时的磁记忆信号特征量Hp(y)Rv和Kmax;Hp(y)RvN和KmaxN为循环加载过程中第N次循环时的磁信号特征量Hp(y)Rv和Kmax。将磁记忆信号特征量数据代入式(3)和式(4)中,得到基于Hp(y)Rv和Kmax的损伤参量D,结果分别见图 7和图 8。
|
图 7 基于Hp(y)Rv的N/Nf-D关系曲线 Fig.7 N/Nf-D relation curve based on Hp(y)Rv |

|
图 8 基于Kmax的N/Nf-D关系曲线 Fig.8 N/Nf-D relation curve based on Kmax |
已知经典连续损伤力学模型中当N=Nf时D=1,而通过式(3)和式(4)计算得到N=Nf时损伤参量D取值范围为0.763~0.912和0.935~0.978,因此分别建立基于Hp(y)Rv和Kmax的疲劳损伤模型,如下式:
| $ {D = 0.763 - P{{\left( {1 - N/{N_{\rm{f}}}} \right)}^{\mathit{\Psi }(\Delta H)}}} $ | (5) |
| $ {D = 0.935 - {P^\prime }{{\left( {1 - N/{N_{\rm{f}}}} \right)}^{{\mathit{\Psi }^\prime }(\Delta H)}}} $ | (6) |
式中:Ψ(ΔH)和Ψ′(ΔH)为损伤累积程度描述函数;P和P′是由材料初始损伤决定的系数。依据式(5)对图 7中N/Nf-D关系曲线进行拟合,拟合结果如下:
| $ \left\{\begin{array}{l} D=0.763-0.78582\left(1-N / N_{\mathrm{f}}\right)^{0.56046} \\ R^2=0.99356 \end{array}\right. $ | (7) |
| $ \left\{\begin{array}{l} D=0.763-0.7371\left(1-N / N_{\mathrm{f}}\right)^{2.79706} \\ R^2=0.95034 \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} D=0.763-0.7615\left(1-N / N_{\mathrm{f}}\right)^{7.81173} \\ R^2=0.96388 \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} D=0.763-0.76304\left(1-N / N_{\mathrm{f}}\right)^{14.03378} \\ R^2=0.93321 \end{array}\right. $ | (10) |
依据式(6)对图 8中N/Nf-D关系曲线进行拟合,拟合结果如下:
| $ \left\{\begin{array}{l} D=0.935-1.06126\left(1-N / N_{\mathrm{f}}\right)^{1.03209} \\ R^2=0.88108 \end{array}\right. $ | (11) |
| $ \left\{\begin{array}{l} D=0.935-0.8873\left(1-N / N_{\mathrm{f}}\right)^{0.2985} \\ R^2=0.95067 \end{array}\right. $ | (12) |
| $ \left\{\begin{array}{l} D=0.935-1.3804\left(1-N / N_{\mathrm{f}}\right)^{0.58618} \\ R^2=0.56097 \end{array}\right. $ | (13) |
| $ \left\{\begin{array}{l} D=0.935-1.05109\left(1-N / N_{\mathrm{f}}\right)^{1.05951} \\ R^2=0.86733 \end{array}\right. $ | (14) |
式中R2为可决系数,最大值为1,越接近1说明拟合程度越好。
图 7、图 8可见,随着循环周次的增加,基于Hp(y)Rv的损伤参量D和基于Kmax的损伤参量D均逐渐增加。相同循环周次下基于Hp(y)Rv损伤参量D随着外加磁场强度的增加而增加,基于Kmax损伤参量D随着外加磁场的增加无明显规律性变化。
对比图 7和图 8,可见,基于Kmax损伤参量D的拟合结果较差,R2较低。基于Hp(y)Rv损伤参量D拟合结果较好,本文优选该参量构建疲劳损伤模型。从图 7及式(7)~式(10)可以看出,基于Hp(y)Rv的损伤模型中,随着外加磁场的增加,Ψ(ΔH)逐渐增加。
继续对式(7)~式(10)中得到的Ψ(ΔH)值进行拟合,结果见图 9。由图可见,Ψ(ΔH)值与外加磁场具有较好的线性关系,因此对其进行线性拟合,拟合关系如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\Psi }(\Delta H) = 0.02435H - 1.24826}\\ {{R^2} = 0.97858} \end{array}} \right. $ | (15) |

|
图 9 Ψ(ΔH)与外加磁场关系曲线 Fig.9 Relation curve between Ψ(ΔH) and applied magnetic field |
将式(15)代入式(5)中,即可得到不同外加磁场下基于Hp(y)Rv的疲劳损伤模型表达式:
| $ D=0.763-P\left(1-N / N_{\mathrm{f}}\right)^{0.02435 H-1.24826} $ | (16) |
该疲劳损伤模型可为外加磁场作用下钢制构件疲劳损伤评估提供方法和模型支持。
4 结论本文以45钢试样为对象,获取了地磁场及外加磁场环境下各损伤阶段的磁记忆信号,并提取了磁场强度法向分量Hp(y)极差值Hp(y)Rv和磁场强度梯度K最大值Kmax,分析了磁记忆特征量的变化规律,结论如下:
1) 在一定外加磁场范围内,各疲劳损伤阶段的Hp(y)曲线均存在过零点,随着损伤程度的增大,Hp(y)的最大值Hp(y)max和最小值绝对值|Hp(y)min|逐渐增大。在Hp(y)过零点处K值随损伤程度的增大呈上升趋势,断裂后Hp(y)max、|Hp(y)min|和K值均达到最大,在断口附近出现了“磁反转”现象。随着外加磁场的增加,Hp(y)max、|Hp(y)min|和断裂后的K值均逐渐增大。
2) Hp(y)Rv和对应于疲劳断裂阶段的Kmax随着外加磁场的增加逐渐增大,且Hp(y)Rv随着疲劳循环周次的增加而增加。
3) 以特征量Hp(y)Rv和Kmax为损伤参量,分别建立了基于Hp(y)Rv和Kmax的疲劳损伤模型,采用Hp(y)Rv构建的模型拟合度更高,可用于开展试样疲劳损伤评估。
| [1] |
SHI Pengpeng, SU Sanqing, CHEN Zhenmao. Overview of researches on the nondestructive testing method of metal magnetic memory: status and challenges[J]. Journal of Nondestructive Evaluation, 2020, 39: 1-37. DOI:10.1007/s10921-020-00688-z |
| [2] |
LIU Bin, ZENG Zhihao, WANG Huipeng. Study on the early fatigue damage evaluation of high strength steel by using three components of metal magnetic memory signal[J]. NDT & E International, 2021, 117: 102380. DOI:10.1016/j.ndteint.2020.102380 |
| [3] |
杨晓惠, 谭川东, 唐名杰, 等. X80管线钢不同变形状态的磁记忆检测试验研究[J]. 材料科学与工艺, 2021, 29(2): 51-57. YANG Xiaohui, TAN Chuandong, TANG Mingjie, et al. Experimental investigation on magnetic memory testing for different deformation states of X80 pipeline steel[J]. Materials Science and Technology, 2021, 29(2): 51-57. DOI:10.11951/j.issn.1005-0299.20190222 |
| [4] |
龙琼, 钟云波, 余正平, 等. 外加磁场下焊接技术的研究现状[J]. 中国材料进展, 2020, 39(6): 472-479. LONG Qiong, ZHONG Yunbo, YU Zhengping, et al. Recent progress in welding technology under external magnetic fields[J]. Materials China, 2020, 39(6): 472-479. DOI:10.7502/j.issn.1674-3962.201908023 |
| [5] |
ZHANG Hong, LIAO Leng, ZHAO Ruiqiang, et al. The non-destructive test of steel corrosion in reinforced concrete bridges using a micromagnetic sensor[J]. Sensors, 2016, 16(9): 1439. DOI:10.3390/s16091439 |
| [6] |
冷建成, 李政达, 王玉洁, 等. 循环应力对磁记忆效应影响的试验研究[J]. 材料导报, 2019, 33(10): 1723-1727, 1733. LENG Jiancheng, LI Zhengda, WANG Yujie, et al. Experimental study on the effect of cyclic stress on magnetic memory effect[J]. Materials Review, 2019, 33(10): 1723-1727, 1733. DOI:10.11896/cldb.18020090 |
| [7] |
WANG Huipeng, DONG Lihong, WANG Haidou, et al. Effect of tensile stress on metal magnetic memory signals during on-line measurement in ferromagnetic steel[J]. NDT & E International, 2021, 117: 102378. DOI:10.1016/j.ndteint.2020.102378 |
| [8] |
邸新杰, 李午申, 白世武, 等. 金属磁记忆检测信号的二维谱熵特征[J]. 焊接学报, 2006(11): 69-72. DI Xinjie, LI Wushen, BAI Shiwu, et al. Two-dimension spectrum entropy feature for metal magnetic memory signal[J]. Transactions of The China Welding Institution, 2006(11): 69-72. DOI:10.3321/j.issn:0253-360X.2006.11.018 |
| [9] |
朱达荣, 潘志远, 刘涛, 等. 金属疲劳过程磁记忆信号多特征量提取研究[J]. 现代制造工程, 2018(10): 123-129. ZHU Darong, PAN Zhiyuan, LIU Tao, et al. The magnetic memory signal wavelet packet frequency band energy feature extraction[J]. Modern Manufacturing Engineering, 2018(10): 123-129. DOI:10.16731/j.cnki.1671-3133.2018.10.020 |
| [10] |
MOONESAN M, KASHEFI M. Effect of sample initial magnetic field on the metal magnetic memory NDT result[J]. Journal of Magnetism and Magnetic Materials, 2018, 460: 285-291. |
| [11] |
HUANG Haihong, QIAN Zhengchun. Effect of temperature and stress on residual magnetic signals in ferromagnetic structural steel[J]. IEEE Transactions on Magnetics, 2016, 53(1): 1-8. DOI:10.1109/TMAG.2016.2613064 |
| [12] |
曹宇, 崔鑫, 纪冬梅. P92钢的蠕变-疲劳损伤行为及蠕变-疲劳损伤本构模型的建立[J]. 机械工程材料, 2021, 45(10): 50-57. CAO Yu, CUI Xin, JI Dongmei. Creep-fatigue damage behavior and establishment of creep-fatigue damage constitutive model of P92 steel[J]. Materials for Mechanical Engineering, 2021, 45(10): 50-57. DOI:10.11973/jxgccl202110007 |
| [13] |
ZHU Wang, MA Zongwei, YAN Jian, et al. Magnetic domain structures and their evolution in quasi-two-dimensional ferromagnet Cr5Te8[J]. Journal of Magnetism and Magnetic Materials, 2020, 512: 167019. DOI:10.1016/j.jmmm.2020.167019 |
| [14] |
杨理践, 郑福印, 高松巍, 等. 基于力磁耦合型的管道电磁应力检测解析模型研究[J]. 仪器仪表学报, 2021, 42(8): 249-258. YANG Lijian, ZHENG Fuyin, GAO Songwei, et al. An analytical model of electromagnetic stress detection for pipeline based on magneto-mechanical coupling model[J]. Chinese Journal of Scientific Instrument, 2021, 42(8): 249-258. DOI:10.19650/j.cnki.cjsi.J2107957 |
| [15] |
REN Shangkun, REN Xianzhi, DUAN Zhenxia, et al. Studies on influences of initial magnetization state on metal magnetic memory signal[J]. NDT and E International, 2019, 103: 77-83. DOI:10.1016/j.ndteint.2019.02.002 |
| [16] |
WANG Ziyi, WU Shengchuan, KANG Guozheng, et al. In-situ synchrotron X-ray tomography investigation on damage mechanism of an extruded magnesium alloy in uniaxial low-cycle fatigue with ratchetting[J]. Acta Materialia, 2021, 211: 116881. DOI:10.1016/j.actamat.2021.116881 |
| [17] |
陈凌, 蒋家羚. 一种新的低周疲劳损伤模型及实验验证[J]. 金属学报, 2005, 41(2): 157-160. CHEN Ling, JIANG Jialing. A new low cycle fatigue damage model and its experimental verification[J]. Acta Metallurgica Sinica, 2005, 41(2): 157-160. DOI:10.3321/j.issn:0412-1961.2005.02.009 |
 2023, Vol. 31
2023, Vol. 31


