金属流变应力是轧制工艺设定以及设备评估的重要参数,在钢的实际生产中,需要掌握奥氏体变形过程中的流变应力。影响奥氏体流变应力的因素很多,包括化学成分、变形温度、变形程度、应变速率等,其中变形温度对金属流变应力的影响较大[1]。金属塑性变形组织结构复杂,各种变形条件对钢流变应力的影响难以用理论进行解析,为了优化轧制工艺以及合理设定设备力能参数,研究不同变形温度下钢的应力-应变曲线变化规律,建立奥氏体应力预测模型至关重要。
目前国内外对于流变应力模型的研究大多集中在高温奥氏体变形条件。Quelennec等[2]研究了高温奥氏体流变应力曲线,研究表明变形过程中发生了动态回复和动态再结晶,位错减少或重排使材料发生软化,在此基础上建立了高温奥氏体流变应力模型。Hernandezi等[3]建立的高温奥氏体流变应力模型由两部分组成:第一部分为硬化和动态回复,第二部分为动态再结晶引起的软化,两者的代数和构成了完整的流变应力表达式。在某一确定变形温度时,当达到临界变形量时即发生动态再结晶,动态再结晶产生的软化量对模型参数有重要影响[4-5]。上述研究主要涉及过冷奥氏体在高温变形条件下流变应力的预测模型。大量研究表明中、低温奥氏体变形能改善高强贝氏体钢相变动力学和组织[6-11],因此,除了高温奥氏体变形,中、低温奥氏体变形过程中的应力-应变规律也需要明确。一般奥氏体冷却过程中先发生铁素体或珠光体转变,当钢中添加合金元素后,在一定冷速下可以避开高温相变区,并在相对较低的温度(低于先共析铁素体相变温度Ar3)下保持全奥氏体组织,此时的奥氏体可以称为过冷奥氏体[12]。
本文拟通过热模拟压缩实验,研究奥氏体应力-应变曲线随温度变化规律,并采用不同应力应变模型对实验数据进行分析,最后提出修正方案,建立适合于本实验钢的奥氏体屈服强度预测模型,为其奥氏体变形工艺提供指导。
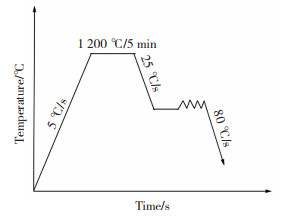
1 实验本实验采用化学成分为0.38C-1.44Si -0.82Mn-0.9Cr-0.25Mo-0.078V(质量分数)的某高强贝氏体钢,取50 kg用真空感应冶炼炉冶炼后,先将铸锭置于1 250 ℃下均匀化处理6 h,然后在900~1 100 ℃的温度范围内进行热轧,通过连续8道次将钢坯从50 mm轧制成12 mm。轧制后,从钢板上取直径5 mm、高10 mm的圆柱形试样,试样径向与轧制方向平行,在Gleeble3500热模拟试验机上进行热模拟压缩实验,工艺如图 1所示。将实验钢以5 ℃/s的速度加热到1 200 ℃,保温5 min,待其充分奥氏体化后以25 ℃/s的速度冷却到不同的变形温度。考虑到不同变形温度对相变、奥氏体强化、位错密度的影响,选取变形温度920、825、800、760和400 ℃(其中920 ℃为全奥氏体区,400~825 ℃为过冷奥氏体区),保温10 s后进行压缩实验,变形速率为0.8 s-1,变形量为20%,实验过程中记录轴向膨胀量和力-位移数据。变形结束后以80 ℃/s的速度冷却到室温,通过力-位移数据可以计算试样在变形过程中的应力-应变。将热模拟实验后的试样进行镶嵌、研磨、抛光、腐蚀(腐蚀剂为体积分数4%的硝酸酒精),使用Keyence金相显微镜观察热模拟实验后的显微组织。
|
图 1 热模拟实验工艺图 Fig.1 Process diagram of thermal simulation experiment |
图 2为变形温度为400 ℃时试样在整个热模拟实验过程中的轴向膨胀量随温度变化曲线。

|
图 2 400 ℃变形试样膨胀量随温度变化曲线(a)和图(a)中矩形区域放大图(b) Fig.2 (a) Expansion of 400 ℃ deformed specimen with temperature and (b) enlarged view of rectangular area in Fig. 2(a) |
从图 2(a)可以看出变形引起的膨胀量变化明显,400 ℃变形后,从400 ℃冷却到室温的过程中发生马氏体相变,如圆形区域标记所示。图 2(b)为图 2(a)中矩形区域的放大图,AB段为试样奥氏体化后的冷却段。可以看出,试样在AB段的膨胀量随温度几乎呈线性变化,说明试样在冷却和等温10 s过程中没有任何相变发生。针对本实验钢,25 ℃/s的冷却速度足以避开高温相变甚至贝氏体相变,因此,试样在变形前(B点)的组织为全奥氏体。同时,可以推断,当变形温度为920、825、800、760 ℃时,试样在变形前的组织均为奥氏体。
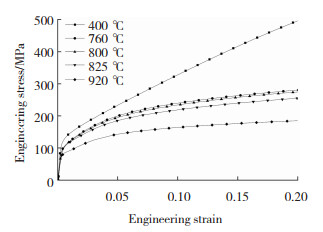
2.2 应力-应变曲线与微观组织图 3为实验钢在不同温度变形时的应力-应变曲线。可以看出,随着变形温度增加,流变应力逐渐减小,且没有观察到明显屈服现象。以产生0.2%残余应变时的应力值作为实验钢的屈服强度,根据截线法测得变形温度为920、825、800、760和400 ℃时,试样的屈服强度分别为85、99、103、104和120 MPa。当温度降为400 ℃时,在塑性变形阶段,试样应力随应变线性增大,呈现出一定冷加工硬化状态,这与试样变形过程中组织变化有关。
|
图 3 高强贝氏体钢的应力应变曲线 Fig.3 Stress-strain curve of high strength bainitic steel |
图 4为不同变形温度下试样的显微组织。由图 4可以看出当变形温度大于等于760 ℃时,组织几乎全为马氏体;当变形温度为400 ℃时,发现较多束状组织,如箭头所示。Eres-Castellanos等[13]研究了奥氏体变形过程中应力诱导马氏体和贝氏体相变,结果表明,确定温度时,当奥氏体应力达到某一临界值,即可诱发贝氏体相变。因此可以推测,400 ℃过冷奥氏体变形时,发生了贝氏体相变,黑色束状组织有可能是变形诱导形成的贝氏体,使基体强度增加,从而导致流变应力急剧增加。

|
图 4 不同变形温度下的OM组织 Fig.4 OM structure at different deformation temperatures: (a) 400 ℃; (b) 760 ℃; (c) 800 ℃; (d) 825 ℃; (e) 920 ℃ |
Medina等[3, 9]提出了高温奥氏体在硬化区域和动态回复区域流变应力模型
| $ \sigma=B[1-\exp (-C \boldsymbol{\varepsilon})]^m $ | (1) |
式中,B、C、m取决于变形条件(变形温度、应变速率),由流变应力曲线进行回归,B、C和m的值可以根据下列公式计算:
| $ B=\left(9.5326+0.6196 \ln \frac{Z}{A}\right)^2 $ | (2) |
| $ C=3.9202\left(\frac{Z}{A}\right)^{0.0592} $ | (3) |
| $ m=0.3449 \exp \left(0.0139 \sqrt{\frac{Z}{A}}\right) $ | (4) |
式中:Z为Zener-Hollomon参数(即温度补偿应变速率参数);A为材料常数。
常数A由下式获得
| $ \begin{aligned} A= & {[12.197+65.590(\text { wt. \% C })-} \\ & 49.052(\text { wt. } \% \mathrm{Nb})] \exp \left(7.076 \times 10^{-5} Q\right) \end{aligned} $ | (5) |
由Zener和Hollomon首次提出的Zener-Hollomon参数表示为
| $ Z=\dot{\varepsilon} \exp \left(\frac{Q}{R T}\right) $ | (6) |
式中:σ为流变应力;ε为应变量;
活化能Q可以根据下列经验公式计算[14]
| $ \begin{aligned} Q= & 26700-2535.52(\text { wt.% } \mathrm{C})+1010(\text { wt. } \% \mathrm{Mn})+ \\ & 33620.76(\text { wt. } \% \mathrm{Si})+35651.28(\text { wt.% } \mathrm{Mo})+ \\ & 93680.52(\text { wt. } \% \mathrm{Ti})^{0.5919}+31673.46(\text { wt. } \% \mathrm{V})+ \\ & 70729.85(\text { wt. } \% \mathrm{Nb})^{0.5649} \end{aligned} $ | (7) |
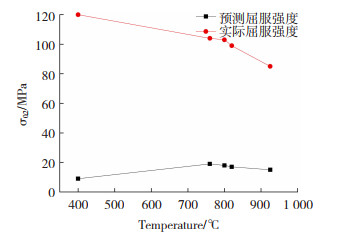
由公式计算本文实验钢的Q为108 596.7 J/mol,最后根据公式(1)~(7),取应变量ε为0.2%,则可以计算不同变形温度下的屈服强度,结果如图 5所示,可以看出模型计算结果与实测结果偏差较大,说明Medina模型无法直接用于本实验钢的奥氏体屈服强度计算。
|
图 5 Medina模型计算的屈服强度与实际屈服强度对比 Fig.5 Comparison between yield strength calculated by Medina model and actual yield strength |
为了更准确的预测试样的屈服强度,在Medina模型的基础上引入参数α,修正后的模型可以表示为
| $ \sigma=\alpha B[1-\exp (-C \varepsilon)]^m $ | (8) |
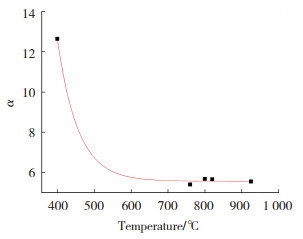
当变形温度为920、825、800、760和400 ℃时,由实验数据拟合所得的α值分别为5.545 578、5.655 915、5.674 137、5.400 483、12.64 556。α随温度变化拟合如图 6所示,当变形温度大于等于760 ℃时,所得的α值很接近。当变形温度为400 ℃时,所得的α值有较大偏差,原因是在400 ℃变形时发生了变形诱导相变,如图 4(a)中的黑色束状组织,导致强度显著增大。因此本试验中的拟合参数可以取变形温度大于或等于760 ℃时所拟合得到的α平均值5.6,添加拟合参数后,预测结果如图 7所示。
|
图 6 拟合参数α随温度变化图 Fig.6 Variation of fitting parameters α with temperature |
|
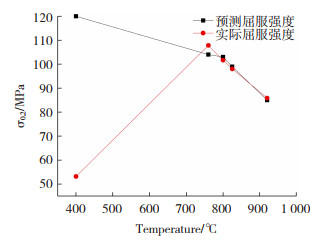
图 7 对Medina模型修正后的理论计算结果与实验值对比 Fig.7 Comparison between theoretical calculation results and experimental values after modification of Medina model |
由图 7可以看出,当变形温度大于等于760 ℃时,使用修正后的模型预测屈服强度,误差不超过5 MPa。而当变形温度为400 ℃时预测结果有较大偏差是由于此时发生了相变,故此模型不适用于预测有相变发生时试样的屈服强度。修正后的屈服强度预测模型可以表示为
| $ \sigma_{0.2}=5.6 B[1-\exp (-0.002 C)]^m $ | (9) |
但需要注意的是公式(9)仅适用于没有发生应变诱导相变时的奥氏体屈服强度预测,当有相变发生时,预测值与实测值有较大差别。考虑α在低温下取值变大,可以建立α与变形温度T的函数关系式,以使公式(9)能准确预测低温变形条件下的奥氏体屈服强度,关于这部分的研究还需要进一步深入。
3.2 Eres-Castellanos模型为了预测确定变形温度、应变速率、化学成分下的屈服强度,Johnson和Cook(JC)[15]与Zerilli-Armstrong(ZA)[16]提出了两个最常用的预测流变应力的模型,表达式为:
| $ \begin{aligned} \sigma= & \left(\sigma_{\mathrm{Yref}}+E \cdot \varepsilon^e\right) \cdot\left(1+D \cdot \ln \left(\frac{\dot{\varepsilon}}{\dot{\varepsilon}_0}\right)\right) \cdot \\ & \left(1-\left(\frac{T_{\mathrm{r}}}{T_{\mathrm{m}}-T_{\mathrm{room}}}\right)^g\right) \end{aligned} $ | (10) |
| $ \begin{aligned} \sigma= & \left(\sigma_{\mathrm{Yref}}+E \cdot \varepsilon^e\right) \exp \left(-A_1 \cdot T_{\mathrm{K}}+\right. \\ & \left.A_2 \cdot T_{\mathrm{r}} \cdot \ln (\dot{\varepsilon})\right) \end{aligned} $ | (11) |
式中:σYref为室温下参考屈服强度;ε为应变量;
Eres-Castellanos等[6]基于JC和ZA模型进行了拓展和优化,采用Nelder-Mead方法对模型参数进行拟合,得出屈服强度σY的两个表达式:
| $ \begin{aligned} \sigma_{\mathrm{Y} 1} & =\left(52.3+47.0 X_{\mathrm{c}}+31.3 X_{\mathrm{Si}}+1.0 X_{\mathrm{Mn}}+\right. \\ & 1.0 X_{\mathrm{Cr}}+31.3 X_{\mathrm{Mo}}+1.3 X_{\mathrm{Ni}}+10.7 X_{\mathrm{V}}+3.8 X_{\mathrm{Al}}+ \\ & \left.16.8 X_{\mathrm{Cu}}+15.2 X_{\mathrm{Ti}}+53(\pm 34)\right) \cdot \\ & \left(1+0.001 \ln \frac{\dot{\varepsilon}}{0.001}\right)\left(1-\left(\frac{T_{\mathrm{r}}}{1487-25}\right)^{0.658}\right) \end{aligned} $ | (12) |
| $ \begin{aligned} \sigma_{\mathrm{Y} 2} & =\left(52.6+50.7 X_{\mathrm{c}}+34.1 X_{\mathrm{Si}}+0.9 X_{\mathrm{Mn}}+\right. \\ & 0.6 X_{\mathrm{Cr}}+34.1 X_{\mathrm{Mo}}+2.3 X_{\mathrm{Ni}}+12.3 X_{\mathrm{V}}+6.5 X_{\mathrm{Al}}+ \\ & \left.19.1 X_{\mathrm{Cu}}+17.4 X_{\mathrm{Ti}}+53(\pm 34)\right) \exp \left(-0.0014 T_{\mathrm{r}}+\right. \\ & \left.\left(0.0111-2.2 \cdot 10^{-5} \cdot T_{\mathrm{r}}\right) \ln \left(\frac{\dot{\varepsilon}}{0.001}\right)\right) \end{aligned} $ | (13) |
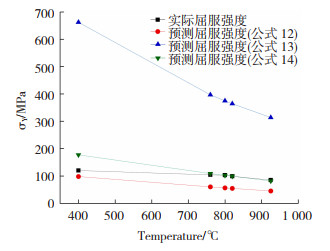
将本文实验钢成分和变形工艺参数代入公式(12)和(13),计算结果如图 8所示,可以看出采用公式(12)计算的结果更接近实验值。上述两个公式在表达形式上有一定差别,公式(12)中第三项为Tr的幂函数,公式(13)中第二项为Tr的指数函数。对比预测结果可知,在考虑变形温度对屈服强度的影响时,应采用幂函数表示其函数关系。由图 8可以看出,公式(12)计算所得的屈服强度与实际屈服强度偏差较小,使用公式(13)计算本实验的屈服强度时出现了较大偏差,特别是变形温度为400 ℃时,预测所得的屈服强度为662 MPa,严重偏离实际屈服强度值。对比公式(12)和公式(13)可得,幂函数更加适用于低应力水平屈服强度的测定,指数函数适用于高应力水平屈服强度的测定。
|
图 8 Eres-Castellanos模型计算屈服强度与实验值对比 Fig.8 Comparison between calculated yield strength of Eres-Castellanos model and experimental values |
为了使公式(12)更准确的用于预测本实验钢的屈服强度,添加拟合参数k,具体形式如下
| $ \begin{aligned} \sigma_{\mathrm{Y}}= & k\left(52.3+47.0 X_{\mathrm{c}}+31.3 X_{\mathrm{Si}}+1.0 X_{\mathrm{Mn}}+\right. \\ & 1.0 X_{\mathrm{Cr}}+31.3 X_{\mathrm{Mo}}+1.3 X_{\mathrm{Ni}}+10.7 X_{\mathrm{V}}+ \\ & \left.3.8 X_{\mathrm{Al}}+16.8 X_{\mathrm{Cu}}+15.2 X_{\mathrm{Ti}}+53(\pm 34)\right) \\ & \left(1+0.001 \ln \left(\frac{\dot{\varepsilon}}{0.001}\right)\right)\left(1-\left(\frac{T_{\mathrm{r}}}{1487-25}\right)^{0.658}\right) \end{aligned} $ | (14) |
通过拟合计算得到k值为1.81,添加拟合参数后预测屈服强度如图 8所示,在不考虑400 ℃下相变发生的情况,预测结果与实际屈服强度偏差不超过4 MPa。由公式(12)添加拟合参数后获得公式(14),使得该模型的预测屈服强度更符合实际屈服强度。需要说明的是,本文拟合的参数仅适用于类似成分的高强贝氏体钢屈服强度的预测,对于化学成分与实验钢相差较大的钢种,需要拟合新的k值,若化学成分相差较大,拟合所得的参数有较大波动。Medina模型和Eres-Castellanos模型都是预测中、低温奥氏体变形应力应变的经典模型,通过本文所做的工作表明,添加拟合参数后Eres-Castellanos模型更加适用于预测0.38C-1.44Si-0.82Mn-0.9Cr-0.25Mo-0.078V钢的屈服强度,能够更好的为此类高强贝氏体钢变形工艺提供指导。
4 结论1) 本文以0.38C-1.44Si-0.82Mn-0.9Cr -0.25Mo-0.078V钢为对象,采用热模拟实验研究了奥氏体变形时,应力-应变随温度的变化规律,随着变形温度增加,应力逐渐降低;随应变量的增加,应力逐渐增大。
2) 结合过冷奥氏体应力-应变曲线和室温显微组织,400 ℃过冷奥氏体变形会诱导相变,相变产生的束状组织会导致应力随应变急剧增加,相对较高温度的全奥氏体变形,呈现更大的加工硬化现象。
3) 基于Medina模型和Eres-Castellanos模型,建立了本实验钢过冷奥氏体屈服强度预测模型,可以为其奥氏体变形工艺提供指导。
| [1] |
阴树标, 刘清友, 孙新军, 等. 高铌钢奥氏体区变形抗力数学模型及试验研究[J]. 昆明理工大学学报(理工版), 2007, 32(2): 21-25. YIN Shubiao, LIN Qingyou, SUN Xinjun, et al. Mathematical model and experimental study on deformation resistance in austenite zone of high Nb steel[J]. Journal of Kunming University of Technology (Science and Technology Edition), 2007, 32(2): 21-25. DOI:10.3969/j.issn.1007-855X.2007.02.006 |
| [2] |
QUELENNEC X, BOZZOLO N, JONAS J J, et al. A new approach to modeling the flow curve of hot deformed austenite[J]. ISIJ International, 2011, 51(6): 945-950. DOI:10.2355/isijinternational.51.945 |
| [3] |
HERNANDEZ C A, MEDINA S F, RUIZ J. Modelling austenite flow curves in low alloy and microalloyed steels[J]. Acta Materialia, 1996, 44(1): 155-163. DOI:10.1016/1359-6454(95)00153-4 |
| [4] |
ZHOU Zijian, ZHANG Rui, CUI Chuanyong, et al. Hot compression behaviors and deformation mechanisms of a Ni-Co-based superalloy with columnar grains[J]. Materials Science & Engineering: A, 2022, 833: 142370. DOI:10.1016/j.msea.2021.142370 |
| [5] |
YANG Chunliang, WU ChuanSong, GAO Song. Modified constitutive equation by using phase field simulation of dynamic recrystallization in friction stir welding[J]. Journal of Materials Research and Technology, 2021, 12: 916-929. DOI:10.1016/j.jmrt.2021.03.031 |
| [6] |
ERES-CASTELLANOS A, TODA-CARABALLO I, LATZ A, et al. An integrated-model for austenite yield strength considering the influence of temperature and strain rate in lean steels[J]. Materials & Design, 2020, 188: 108435. DOI:10.1016/j.matdes.2019.108435 |
| [7] |
JIANG F L, TAKAKI S, MASUMURA T, UEMORI R, et al. Nonadditive strengthening functions for cold-worked cubic metals: experiments and constitutive modeling[J]. International Journal of Plasticity, 2020, 129: 102700. DOI:10.1016/j.ijplas.2020.102700 |
| [8] |
丁会明. 奥氏体不锈钢低温本构模型及其应用研究[D]. 杭州: 浙江大学, 2019: 60-86. DING Huiming. Study on low temperature constitutive model of austenitic stainless steel and its application[D]. Hangzhou: Zhejiang University, 2019: 60-86. |
| [9] |
MEDINA S F, HERNANDEZ C A. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels[J]. Acta Materialia, 1996, 44(1): 137-148. DOI:10.1016/1359-6454(95)00151-0 |
| [10] |
刘曼, 胡海江, 田俊羽, 等. 变形对超高强贝氏体钢组织和力学性能的影响[J]. 金属学报, 2021, 57(6): 749-756. LIU Man, HU Haijiang, TIANG Junyu, et al. Effect of deformation on microstructure and mechanical properties of ultra-high strength bainitic steel[J]. Acta Metallurgica Sinica, 2021, 57(6): 749-756. DOI:10.11900/0412.1961.2020.00310 |
| [11] |
TANG Wanru, LIU Shimeng, LIU Zheng. High strain rate compression deformation mechanism and constitutive equation of fine grained Mg-7Gd-5Y-1.2Nd-0.5Zr alloy at different temperatures[J]. Materials Science & Engineering: A, 2020, 780: 139208. DOI:10.1016/j.msea.2020.139208 |
| [12] |
崔忠圻, 覃耀春. 金属学与热处理[M]. 第二版. 北京: 机械工业出版社, 2017: 239-140. CUI Zhongqi, QIN Yaochun. Metallography and heat treatment[M]. 2nd ed. Beijing: China Machine Press, 2017: 239-240. |
| [13] |
ERES-CASTELLANOS A, CABALLERO F G, GARCIA-MATEO C. Stress or strain induced martensitic and bainitic transformations during ausforming processes[J]. Acta Materialia, 2020, 189: 60-72. DOI:10.1016/j.actamat.2020.03.002 |
| [14] |
SHIRAISHI R. Modeling of the dynamic transformation above the Ae3 temperature[D]. Hamilton: McMaster University, 2018: 29-31.
|
| [15] |
JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48. DOI:10.1016/0013-7944(85)90052-9 |
| [16] |
ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations[J]. Applied Physics, 1987, 61(5): 1816-1825. DOI:10.1063/1.338024 |
 2023, Vol. 31
2023, Vol. 31


