2. 河北省智能装备数字化设计及过程仿真重点实验室(唐山学院),河北 唐山 063000;
3. 唐山亚特专用汽车有限公司,河北 唐山 063000
2. Key Laboratory of Intelligent Equipment Digital Design and Process Simulation of Hebei Province (Tangshan University), Tangshan 063000, China;
3. Tangshan Yate Special Vehicle Co., Ltd., Tangshan 063000, China
胀压成形工艺是制造汽车桥壳的先进技术,所得桥壳具有壁厚分布合理、机械性能良好且无焊缝等优点[1-2]。制造胀压成形桥壳,首先需要对初始管坯进行端部缩径,目前管坯端部缩径工艺使用的是推压缩径。对于无芯轴推压缩径,Yong等[3]以薄壁铜管为例,分析了管坯变形缺陷发生的机理,并进行了实验验证;Kishimoto等[4]研究了工艺参数对管坯的成形质量的影响;Ameli等[5]研究了缩径管坯的残余应力变化规律,并进行了实验测定。对于芯轴推压缩径,滕宏春等人[6]对固定芯轴和动芯轴两种形式的变形力进行了解析,并进行了实验验证;Teng等[7]分析了芯轴推压缩径工艺参数对管件起皱的影响;张双杰等[8]对固定芯轴的推压缩径工艺的变形过程进行了理论分析,揭示出工艺参数对变形的影响规律;李攀等[9]对管件端部的整形载荷进行了求解,同时确定了芯轴加工速度和凹模半锥角对成形的影响规律;刘恒等[10]针对推压缩径存在的端部翘曲进行了分析,得到了翘曲变形的特征,并推导了残余应力与变形的关系表达式。无芯轴推压缩径管坯存在壁厚增加量大、端部翘曲及部分管坯端部轴向开裂等现象[11],且初始管坯存在的壁厚偏差会影响产品的使用性能[12]。针对以上问题,可采用推压-拉拔复合缩径工艺进行管坯两端缩径。对于推压-拉拔复合缩径工艺,已有学者针对管坯壁厚偏差、芯轴外径等工艺参数对成形的影响规律进行了一定的研究[13-14],并使用主应力对缩径应力进行了解析[15]。推压-拉拔复合缩径成形过程中,芯轴以大于管坯的伸长速度向管坯端部拉出,芯轴对变形管坯有一定的拉拔作用,该作用只是由管坯与芯轴之间的摩擦力来实现,其间的摩擦系数对成形有重要的影响,但目前对芯轴摩擦系数影响规律的研究尚未见报道。
本文基于推压-拉拔复合缩径的成形过程,分析了芯轴摩擦系数对成形的影响规律,针对具体实例,应用有限元仿真方法,得到了芯轴摩擦系数的设置范围,并进行了实验验证,为工程实践提供了根据。
1 推压-拉拔复合缩径变形分析图 1为推压-拉拔复合缩径的成形过程。初始管坯半径为R0,壁厚为t0。缩径后,管坯半径为R1,由于缩径凹模及芯轴的共同作用,壁厚值受到了控制。缩径管坯以速度v1向外自然伸长。凹模在凹模推力Fa的作用下以速度va由管坯外端向内部进给。缩径凹模半锥角为α,凹模出口处半径为R2,凹模过渡圆角半径为Ra。同时,管坯内部芯轴在拉力Fm作用下以速度vm由管坯内部向外端运动。芯轴外拉速度vm大于管坯的伸长速度v1,芯轴半径为Ri。
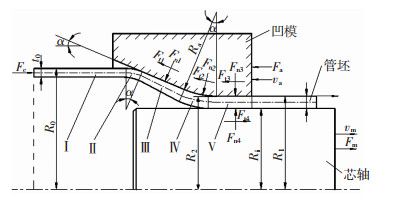
|
图 1 推压-拉拔复合缩径力学模型 Fig.1 Mechanical model of pushing-pulling necking Ⅰ—传力区;Ⅱ—入口弯曲区;Ⅲ—锥模减径区;Ⅳ—出口弯曲区;Ⅴ—芯轴作用区 |
缩径管坯分为5个变形区:传力区,入口弯曲区,锥模减径区,出口弯曲区以及芯轴作用区。设定管坯圆周方向为纬向,壁厚方向为法向,垂直以上两个方向的为经向。
在管坯传力区,质点单元近似处于单向压应力状态,其合力为传力区的经向抗力Fc;在管坯入口弯曲区,管坯金属发生经向弯曲变形;在管坯锥模减径区,管坯外表面受到凹模锥面作用的法向压力Fn1及切向摩擦力Ft1;在管坯出口弯曲区,管坯外表面受到凹模过渡圆弧面作用的法向压力Fn2及切向摩擦力Ft2;在芯轴作用区,减径后管坯的外表面与凹模的内壁接触,受到法向压力Fn3与切向摩擦力Ft3的作用,管坯内表面与芯轴外表面接触,受到芯轴的法向压力Fn4及切向摩擦力Ft4作用,摩擦力Ft4与芯轴移动方向相同,相当于对管坯作用了一定的拉拔力。针对管坯、缩径凹模与芯轴的整个系统而言,根据轴线方向受力平衡条件,管坯传力区抗力Fc应为
| $F_{\mathrm{c}}=F_{\mathrm{a}}-F_{\mathrm{t} 4}$ | (1) |
较大的摩擦系数使得摩擦力Ft4增大,传力区管坯的抗力Fc减小,降低了管坯失稳的可能性。变形时,芯轴作用区金属内外表面受到方向不同的摩擦剪切应力作用,较大的摩擦系数使金属受到的摩擦剪切应力作用增强,在一定程度上降低了缩径管坯的变形抗力,有利于减小凹模推力和芯轴拉拔力。较小的摩擦系数将减小摩擦力Ft4,致使传力区管坯的抗力Fc增大,可能导致传力区管坯轴向压应力过大,从而发生塑性变形,出现起皱失稳现象。
2 有限元模拟 2.1 研究对象以某载重6.5 t胀压成形汽车桥壳第一道次推压-拉拔复合缩径工艺为例,如图 2所示,初始管坯外径为Φ219 mm,壁厚t0为7.5 mm,长度L0为1 380 mm。变形后,管坯传力区长度L1为456 mm,外径为Φ190 mm;凹模半锥角α为23°,材料为40Cr。
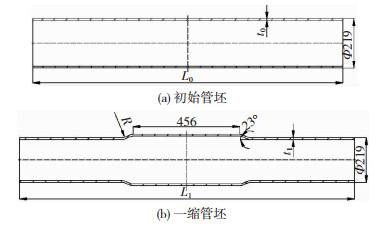
|
图 2 第一道次复合缩径工艺图(单位:mm) Fig.2 First pass of pushing-pulling necking: (a)initial tube blank; (b)first pass necking tube blank |
管坯选用Q345B无缝钢管,通过拉伸实验得到材料真实应力-应变关系为。管坯密度为7 800 kg/m3,弹性模量为2.1×105 MPa,硬化指数为0.2,泊松比为0.3,屈服极限为345 MPa,强度极限为612 MPa。
2.2 有限元模型变形过程的有限元模拟使用ABAQUS软件。因为管坯和缩径模具都为轴对称结构,在软件中建立了1/4有限元模型,如图 3所示。管坯网格为四面体单元类型。夹持模内径为219 mm,长度为125 mm;缩径凹模进给位移量为462.0 mm,芯轴外拉位移量为52.5 mm;芯轴外径为173.8 mm。将对称边界条件设置在管坯对称面上,设置了模具的位移约束,并在分析步中完成凹模推压、芯轴拉拔、退模等动作。模具设置为解析刚体,管坯与模具之间设置为刚-柔关系,并设定不同的芯轴摩擦系数进行仿真。
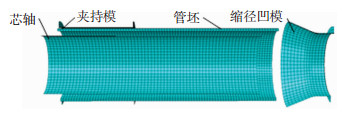
|
图 3 仿真模型 Fig.3 FEM simulation model |
设定芯轴与管坯间的接触动摩擦系数μ分别为0.05、0.10、0.15、0.20、0.25和0.30进行有限元仿真。缩径凹模与管坯间的接触动摩擦系数设定为0.10,夹持模与管坯间的接触动摩擦系数设定为0.15。
图 4为μ=0.05时管坯的模拟结果,管坯传力区的经向压应力极大值σρ为393.92 MPa,超过屈服极限σs,管坯传力区发生塑性变形,出现起皱现象,起皱处最大外径为Φ228.07 mm,凸起量为4.54 mm。管坯芯轴作用区外径为Φ190.25 mm,壁厚为8.10 mm。管端外径为Φ190.38 mm,无翘曲现象。凹模推力为2415.76 kN,芯轴拉拔力为888.39 kN。
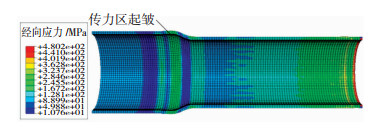
|
图 4 μ=0.05时模拟结果 Fig.4 Simulation results when μ=0.05 |
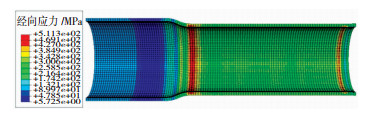
图 5为μ=0.10时管坯的模拟结果,管坯传力区经向压应力极大值σρ为326.01 MPa,未出现起皱失稳。管坯芯轴作用区外径为Φ190.52 mm,壁厚为8.11 mm。管端外径为Φ190.39 mm,无明显翘曲。凹模推力为2063.70 kN,芯轴拉拔力为823.74 kN。
|
图 5 μ=0.10时模拟结果 Fig.5 Simulation results when μ=0.10 |
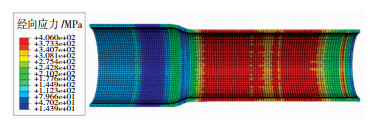
图 6为μ=0.15时管坯的模拟结果,管坯传力区经向压应力极大值σρ为281.19 MPa,未出现起皱失稳。管坯芯轴作用区外径为Φ190.19 mm,壁厚为8.11 mm。管端外径为Φ190.40 mm,无明显翘曲。凹模推力为1749.79 kN,芯轴拉拔力为579.12 kN。
|
图 6 μ=0.15时模拟结果 Fig.6 Simulation results when μ=0.15 |
对不同μ值缩径后管坯的几何参数、传力区经向压应力σρ及凹模推力和芯轴拉拔力进行测量,其测量值见表 1。
| 表 1 不同芯轴摩擦系数μ模拟结果 Table 1 Simulation results under different friction coefficient μ |
由以上测量结果可知:
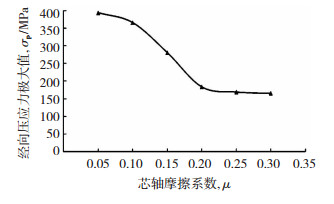
1) 随着μ的增大,管坯传力区的经向压应力极大值σρ随之减小。图 7为σρ随μ的变化曲线,当μ由0.05增加至0.20时,σρ由393.92 MPa迅速减小至183.59 MPa;当μ由0.20增加至0.30时,σρ逐渐减小至165.54 MPa。
|
图 7 σρ随μ的变化曲线 Fig.7 Variation curve of σρ with μ |
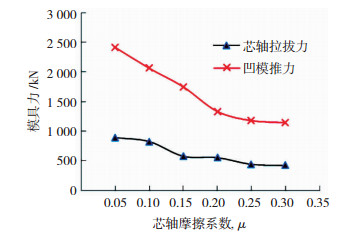
2) 随着μ的增大,凹模推力Fa与芯轴拉拔力Fm随之减小。图 8为Fa与Fm随μ的变化曲线,当μ由0.05增加至0.20时,Fa由2 415.76 kN减小至1 333.41 kN;当μ由0.20增加至0.30时,Fa逐渐减小至1 144.51 kN。当μ由0.05增加至0.30时,Fm由888.39 kN逐渐减小至426.99 kN。
|
图 8 凹模推力和芯轴拉拔力随μ的变化曲线 Fig.8 Variation curve of die pushing force and mandrel pulling force with μ |
基于传力区不失稳,即传力区轴向压应力σρ≤0.9σs,同时考虑当μ≥0.20时,轴向压应力、凹模推力和芯轴拉拔力变化不大。确定第一道次推压-拉拔复合缩径的芯轴摩擦系数μ取值范围为0.12≤μ≤0.20。
3 缩径实验 3.1 实验装备缩径实验在THP63-200型三向液压机上进行,如图 9所示。

|
图 9 推压-拉拔复合缩径专用液压机与模具 Fig.9 Equipment and die of pushing-pulling necking 1—上滑块 2—上夹持模 3—上模座 4—左滑块 5—左支撑筒 6—左缩径凹模 7—左芯轴 8—下夹持模 9—下模座 10—右芯轴 11—右缩径凹模 12—右支撑筒 13—右滑块 |
上滑块1固定上夹持模2,实现垂向移动,最大工作压力为2 000 kN;下模座9固定下夹持模8,固定不动;左右支撑筒(5、12)固定缩径凹模(6、11),最大工作压力为3 000 kN,实现凹模的水平方向移动;左右中心缸安装在侧缸中,用来固定芯轴(7、10),实现芯轴的水平方向移动,最大工作压力为1 000 kN。左缩径凹模6、右缩径凹模11分别固定于左支撑筒5和右支撑筒12上,左右支撑筒分别固定于液压机左滑块4和右滑块13上,左芯轴7和右芯轴10分别与液压机左右中心活塞相连,上夹持模2固定于上模座3上,下夹持模8固定在下模座9上,上模座连固定在液压机上滑块1上,下夹持模8通过下模座9固定在工作台上。
依据图 2所示的工艺选取一根初始管坯,在多动作液压机上进行缩径实验,实验条件与模拟条件相同。对左右两侧芯轴表面施加不同的润滑措施,如图 10所示。将右芯轴外壁涂抹乳化液,芯轴外壁与管坯内表面接触动摩擦系数μ近似为0.10;左芯轴不采用润滑措施,μ近似为0.15;左右缩径凹模与管坯间使用乳化液进行润滑,μ近似为0.10;夹持模与管坯间不润滑,μ近似为0.15。缩径时,上夹持模向下移动,与下夹持模合模后,对管坯的传力区进行夹持,夹持压力为50 kN,缩径凹模进给位移量462.0 mm,芯轴向外拉拔的位移量52.5 mm,记录左右两侧管坯变形时的凹模推力Fa与芯轴拉力Fm。

|
图 10 芯轴不同润滑措施 Fig.10 Different lubrication methods of mandrel |
图 11为缩径后管坯,管坯两侧皆能够顺利完成缩径,管件成形较好,未出现屈服起皱。测量不同润滑措施所得管坯的外形尺寸及壁厚值,记录管坯变形时凹模推力和芯轴拉力。当μ=0.10时,管侧直臂区长度为454.74 mm,伸长量为32.90 mm,芯轴作用区的管坯外径为190.14 mm,端部外径为190.68 mm,芯轴作用区的管坯壁厚为8.06 mm。凹模推力Fa1与芯轴拉力Fm1分别为2 256.47、905.21 kN;当μ=0.15时,管侧直臂区长度为452.24 mm,伸长量为31.66 mm,芯轴作用区的管坯外径为189.88 mm,端部外径为190.62 mm,芯轴作用区的管坯壁厚为8.10 mm。凹模推力Fa2与芯轴拉力Fm2分别为2 034.24、771.11 kN。

|
图 11 芯轴不同润滑措施所得管坯 Fig.11 Tube blank obtained with different lubrication methods of mandrel |
表 2为实验与模拟结果的对比,考虑到模具装配所致附加阻力等因素,实际凹模推力和芯轴拉拔力较大。Fa2、Fm2较Fa1与Fm1减小了9.85%、14.81%。缩径管件的几何尺寸、凹模推力和芯轴拉拔力与仿真数值接近,验证了仿真的正确性。
| 表 2 模拟与实验结果对比 Table 2 Comparison between simulation and test results |
1) 随着μ的增加,管坯传力区轴向压应力减小,缩径凹模推力和芯轴拉拔力减小。较小的摩擦系数可能导致轴向压应力过大而失稳起皱。较大的摩擦系数,有利于降低轴向压应力,但易造成管坯表面划伤,对于后期管坯的服役可能会造成影响。
2) 基于轴向不失稳,较小的凹模推力和芯轴拉拔力,确定了第一道次推压-拉拔复合缩径的芯轴摩擦系数μ取值范围为0.12≤μ≤0.20。
3) 设置两组不同外径的芯轴摩擦系数进行了实验,实验结果与模拟结果相吻合,证明了有限元仿真的可靠性。
| [1] |
吴娜, 刘超, 王晓迪. 小型汽车桥壳液压胀形加工方法的研究现状[J]. 塑性工程学报, 2020, 27(9): 12-19. WU Na, LIU Chao, WANG Xiaodi. Research status on hydro-bulging processing method of small automobile axle-housing[J]. Journal of Plasticity Engineering, 2020, 27(9): 12-19. DOI:10.3969/j.issn.1007-2012.2020.09.002 |
| [2] |
王晓迪, 王连东, 金淼, 等. 汽车桥壳多向充液压制小圆弧成形分析及设计[J]. 吉林大学学报(工学版), 2022, 52(5): 998-1008. WANG Xiaodi, WANG Liandong, JIN Miao, et al. Forming analysis and design for small arc in multi direction hydro pressing of auto mobile axle housing[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(5): 998-1008. DOI:10.13229/j.cnki.jdxbgxb20210195 |
| [3] |
YONG Li, HUANG Jin long, HUANG Guang wen, et al. Comparison of radial forging between the two and three-split dies of a thin-walled copper tube during tube sinking[J]. Materials and Design, 2014, 56: 822-832. DOI:10.1016/j.matdes.2013.11.079 |
| [4] |
KISHIMOTOT, SAKAGUCHI H, SUEMATSU S, et al. Outer diameter and surface quality of micro metal tubes in hollow sinking[J]. Procedia Manufacturing, 2020(47): 217-223. DOI:10.1016/j.promfg.2020.04.192 |
| [5] |
AMELI A, MOVAHHEDY M. A parametric study on residual stresses and forging load in cold radial forging process[J]. International Journal of Advanced Manufacturing Technology, 2007, 33(12): 7-17. DOI:10.1007/s00170-006-0453-2 |
| [6] |
滕宏春, 林桂霞, 胡平. 带有动芯轴的管料壁厚减薄缩口成形的理论解析[J]. 机械工程学报, 2005, 41(7): 234-238. TENG Hongchun, LIN Guixia, HU Ping. Theoretical analysis and experiment of sinking of tube with a moving mandrel[J]. Journal of Mechanical Engineering, 2005, 41(7): 234-238. |
| [7] |
TENG Hongchun, TENG Bingyan. An optiming process design for sinking with the thin-wall cylindrical cup[J]. Applied Mechanics and Materials, 2014, 456: 22-27. DOI:10.4028/www.scientific.net/AMM.456.22 |
| [8] |
张双杰, 李强, 王丽娟, 等. 厚壁管件有芯棒开式冷挤压成形极限分析[J]. 机械工程学报, 2010, 46(22): 53-57. ZHANG Shuangjie, LI Qiang, WANG Lijuan, et al. Analysis on the forming limit of cold open-die extrusion with mandrel for the thick-walled tube[J]. Journal of Mechanical Engineering, 2010, 46(22): 53-57. DOI:10.3901/JME.2010.22.053 |
| [9] |
李攀, 罗建国, 陈彬, 等. 驱动桥壳阶梯轴内壁精密整形工艺设计及理论解析[J]. 塑性工程学报, 2020, 27(8): 10-17. LI Pan, LUO Jianguo, CHEN Bin, et al. Design and theoretical analysis of inner wall precise reshaping technology for stepped shafts of drive axle housing[J]. Journal of Plasticity Engineering, 2020, 27(8): 10-17. DOI:10.3969/j.issn.1007-2012.2020.08.002 |
| [10] |
刘恒, 王连东, 王晓迪, 等. 管坯大变形自由推压缩径残余应力的研究[J]. 中国机械工程, 2021, 32(11): 1354-1360. LIU Heng, WANG Liandong, WANG Xiaodi, et al. Study on the residual stress of large deformatin free pushing diameter-reducing tube blanks[J]. China Mechanical Engineering, 2021, 32(11): 1354-1360. DOI:10.3969/j.issn.1004-132X.2021.11.012 |
| [11] |
LIU H, WANG L D, WANG X D, et al. Analysis and control of cracking and wrinkling at the end of seamless steel tube with multi-pass large deformation diameter-reducing[J]. Metals Open Access Metallurgy Journal, 2021, 11(9): 1438. DOI:10.3390/met11091438 |
| [12] |
王连东, 梁晨, 马雷, 等. 管坯双侧反向芯轴推压缩径模具及工艺: 201310191757.9[P]. 2015-05-13.
|
| [13] |
王连东, 刘超, 刘恒, 等. 芯轴外径对大变形推压-拉拔复合缩径的影响[J]. 中国机械工程, 2018, 29(17): 2131-2136. WANG Liandong, LIU Chao, LIU Heng, et al. Effects of mandrel diameters on large deformation pushing-pulling necking[J]. China Mechanical Engineering, 2018, 29(17): 2131-2136. DOI:10.3969/j.issn.1004132X.2018.17.017 |
| [14] |
刘超, 王连东, 刘恒, 等. 带壁厚偏差的无缝钢管推压-拉拔复合缩径[J]. 中国机械工程, 2018, 29(11): 1375-1379, 1385. LIU Chao, WANG Liandong, LIU Heng, et al. Study on seamless steel tube with wall thickness deviation in pushing-pulling necking[J]. China Mechanical Engineering, 2018, 29(11): 1375-1379, 1385. DOI:10.3969/j.issn.1004-132X.2018.11.019 |
| [15] |
刘超, 吴娜, 杨志安. 推压-拉拔复合缩径成形的理论解析[J]. 塑性工程学报, 2021, 28(10): 199-205. LIU Chao, WU Na, YANG Zhian. Theoretical analysis of pushing-pulling necking[J]. Journal of Plasticity Engineering, 2021, 28(10): 199-205. DOI:10.3969/j.issn.1007-2012.2021.10.025 |
 2023, Vol. 31
2023, Vol. 31


