2. 省部共建有色金属先进加工与再利用国家重点实验室(兰州理工大学),兰州 730050
2. State Key Laboratory of Advanced Processing and Recycling of Nonferrous Metals (Lanzhou University of Technology), Lanzhou 730050, China
随着国家对“碳达峰”和“碳中和”战略的推进,建立低碳、绿色、高效能源体系和制造体系是重要的发展方向。汽车等生产行业逐渐使用轻质合金和铝钢复合结构等对焊接工艺要求较高的热敏感材料代替传统钢铁结构。目前已有部分焊接工艺能够实现对热敏感材料的有效焊接,如激光焊[1-2]、激光电弧复合焊[3-4]、搅拌摩擦焊[5-6]等,但这些工艺生产成本较高,应用受限。本文所研究的双弧脉冲MIG焊是在脉冲旁路耦合电弧焊[7]的基础上提出的一种低能量输入的焊接方法,在传统MIG焊的基础上,引入TIG旁弧,分流流经母材的电流,从而减少母材的热输入,且旁弧的引入有利于促进熔滴过渡,同时主旁弧均采用脉冲电源,可进一步降低母材热输入,保证在较小的母材热输入下实现熔滴的稳定过渡[8],能够满足质量的低能量输入焊接,适用于对热敏感材料的焊接。但相较于传统MIG焊,由于双弧脉冲MIG焊采用脉冲电源,电弧自调节作用弱,仍存在焊接耦合电弧稳定性差、多参数匹配困难等难题。因此,深入研究耦合电弧的物理特性、优化多参数调控机制是双弧脉冲MIG焊亟待解决的关键问题。
随着数值分析理论和计算机技术的提高,数值模拟方法在焊接领域获得广泛应用。Tomasz[9]、Ahmed[10]、Bataev[11]、Iqbal[12]和何俊杰等[13]通过数值模拟方法对电弧、焊缝、熔池等进行物理特性分析,为激光焊、爆炸焊、搅拌摩擦焊、CMT等焊接工艺的改进提供理论支持。石玗等[14]对脉冲电流作用下TIG电弧进行了数值模拟,分析了不同脉冲电流参数作用下的电弧温度和压力的变化情况。Ogino等[15]通过数值模拟分析了不同钨极间距下双TIG电弧行为和热输入特性。石玗等[16]对旁路耦合电弧焊的温度场进行了模拟,分析了焊接参数对母材热输入的影响。王新鑫等[17-18]建立了双钨极耦合电弧三维瞬态模型,对耦合电弧进行了数值模拟,分析了不同钨极间距和不同弧长对耦合电弧的温度场、流场、电弧压力和电流密度的影响,并模拟了电弧-熔池的传热与流动,分析了电弧和熔池的相互影响。宗然等[19]通过数值模拟方法研究了电极相对位置和焊接电流对于TIG-MIG复合焊的电弧稳定性和焊缝成形的影响。方乃文等[20-21]对DE-GMAW焊接工艺的焊接温度场和应力场进行了数值模拟,为焊接残余应力的研究提供理论支持。Rodríguez-Hernández等[22]对比研究了GTAW-GMAW和GMAW两种焊接工艺,结果表明GTAW-GMAW工艺能够有效减少焊缝金属的晶粒组织和孔隙率,提高焊接质量。陈姬[23-25]和崔双双[26]等针对TIG-MIG复合焊系统,先后研究焊枪夹角、电弧间相互作用、焊接电流及丝极间距对TIG-MIG电弧及焊接过程的影响,为TIG-MIG复合焊的优化研究提供了理论支持。
针对双弧脉冲MIG焊耦合电弧稳定性差的问题,本文采用数值模拟的方法对双弧脉冲MIG焊耦合电弧的物理特性进行研究,以提高耦合电弧稳定性和焊接工艺性能。通过对不同脉冲电流作用下的耦合电弧进行瞬态数值模拟,对比分析了主旁弧峰值电流对耦合电弧形态、温度场及电弧压力的影响规律,并进行了实验验证,以期为双弧脉冲MIG焊耦合电弧稳定性多参数调控提供理论支持。
1 数学模型考虑到双弧脉冲MIG焊焊接过程中,实验环境和设备因素对耦合电弧的影响,在双弧脉冲MIG焊耦合电弧的数值模拟过程中,对三维瞬态数学模型做出以下假设:
1) 耦合电弧等离子体为连续介质,且处于局部热平衡状态;
2) 耦合电弧区为纯氩气环境,处于不可压缩状态;
3) 耦合电弧是光学薄的,对热量辐射的重吸收忽略不计;
4) 流体计算域中等离子体的状态为层流状态;
5) 不考虑焊丝及母材熔化带来的金属蒸发。
1.1 控制方程1) 质量连续性方程
| $ \frac{\partial \rho}{\partial t}+\nabla \cdot(\rho v)=0 $ | (1) |
2) 动量守恒方程
| $ \frac{\partial}{\partial t}(\rho v)+\nabla \cdot(\rho v v)=-\nabla P+\rho g+F $ | (2) |
式中:ρ为密度;v为速度;P为压力;g为重力加速度;F为体积力。
3) 能量守恒方程
| $ \frac{\partial}{\partial t}(\rho h)+\nabla \cdot(\rho v h)=\nabla \cdot\left(\frac{k}{C_p} \nabla \cdot h\right)+Q $ | (3) |
式中:ρ为密度;P为压力;Fx、Fy、Fz为体积力在x、y、z方向的分量;Cp为比热容;k为导热系数;Q为能量方程的源项,由焊丝和钨极产生的焦耳热、电子运输晗以及辐射散射组成。
4) 麦克斯韦方程组
① 电流连续性方程
| $ \nabla \cdot(\sigma \nabla \phi)=0 $ | (4) |
② 欧姆定律
| $ j=-\sigma(\nabla \phi) $ | (5) |
③ 磁矢势泊松方程
| $ -\nabla^2 A=\mu_0 j $ | (6) |
| $ B=\nabla \times A $ | (7) |
式中:σ为电导率;ϕ为电势;j为电流密度;μ0为真空磁导率;A为磁矢势;B为磁通密度。
通过Fluent进行数值模拟的过程中,材料的热物理参数[27-28]、动量守恒方程和能量守恒方程的源项以及电流连续性方程均通过UDF(用户自定义函数)和UDS(用户自定义标量)在Fluent控制面板中进行添加。
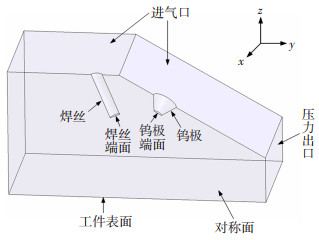
1.2 几何模型和边界条件基于双弧脉冲MIG焊实验平台建立了双弧脉冲MIG焊耦合电弧关于yoz面对称的三维几何模型,为了便于计算,对几何模型进行了简化,如图 1所示。
|
图 1 几何模型 Fig.1 Geometric model |
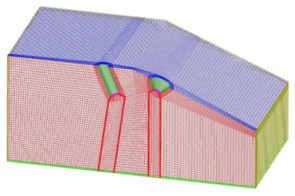
由于耦合电弧物理场变化较为复杂,对焊丝和钨极周围及下方变量梯度较大的区域进行局部加密,生成网格数约为40万,网格划分如图 2所示。
|
图 2 网格划分 Fig.2 Meshing |
数值模拟过程中,速度入口和压力出口与电弧距离较近,温度不能设置为室温,而设为1 000 K,焊丝和钨极壁面及端部温度设为2 000 K,工件表面温度设为5 000 K;将焊丝、钨极和工件表面设为固体壁面,流动速度为0,进气口设为速度入口,速度为u=Q/A, Q为保护气流量,A为进气口面积,压力出口设置为单向压力出口,相对压力P=0。焊丝和钨极端部以及工件表面有电流经过,其中工件表面电势为0,其他边界认为无电流通过。焊接过程中,MIG焊的保护气流量为20 L/min,TIG焊的保护气流量为5 L/min。具体的边界条件如表 1所示。
| 表 1 边界条件 Table 1 Boundary conditions |
在进行数值模拟时,为了减少计算时间,初始温度设置为T0=12 000 K,假设电弧已经处于起弧状态,磁矢势A=0,初始速度ν=0,初始电势ϕ=0。首先进行稳态计算,当电弧稳定后进行瞬态计算。
本文对5组脉冲电流作用下的双弧脉冲MIG焊耦合电弧进行数值模拟,数值模拟过程中所采用的主旁弧脉冲电流为同频脉冲电流,主旁弧脉冲频率均为f=80 Hz,占空比均为δ=20%,具体脉冲电流参数如表 2所示。
| 表 2 脉冲电流参数 Table 2 Pulse current parameters |
本文依据数值模拟结果对双弧脉冲MIG焊耦合电弧形态变化、温度及电弧压力的分布及变化情况进行讨论,分析了脉冲电流参数对耦合电弧物理特性的影响规律。
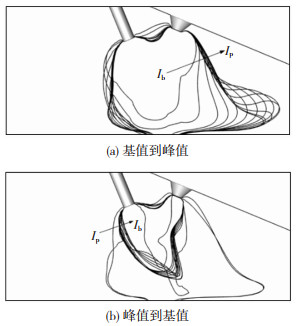
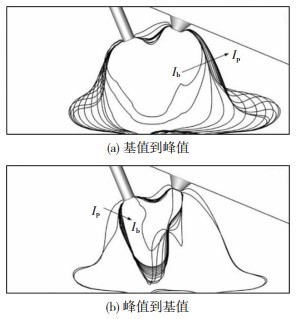
2.1 耦合电弧形态参考文献[14],耦合电弧形态取yoz截面上的10 000 K等温线进行表示。在耦合电弧形态变化图中,当电流从基值阶跃为峰值后,每两条等温线的时间间隔为0.2 ms;当电流从峰值跳变为基值后,前1 ms每两条等温线的时间间隔为0.2 ms,而后为1 ms。
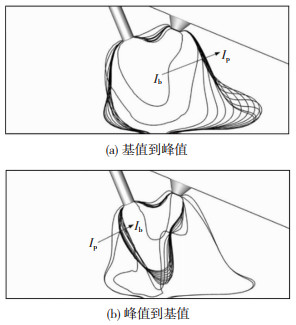
由图 3~图 7分别对应5组脉冲电流参数作用下一个脉冲周期内耦合电弧形态变化,可以看出,当脉冲电流发生跳变时,双弧脉冲MIG焊耦合电弧的形态随之改变,随着时间的进行,变化幅度逐渐减小,最终达到相对稳定的状态。与文献[6] 不同的是,由于旁弧的影响,耦合电弧形态在yoz截面上并不是呈现钟罩型,而是整体呈驼峰状。
|
图 3 IP=195 A, |
|
图 4 IP=145 A, |

|
图 5 IP=70 A, |

|
图 6 IP=70 A, |
|
图 7 IP=70 A, |
图 3~图 5分别为
对比图 3(b)、图 4(b)以及图 5(b),当IP为70、145和195 A时,在脉冲电流从峰值跳变为基值后,耦合电弧达到相对稳定状态所需的时间分别为5、7、8 ms。对比耦合电弧的形态可知,当主弧峰值电流较小时,耦合电弧形态一直呈现稳定的驼峰状;而当主弧峰值电流较大时,在跳变为基值电流的过程中,耦合电弧形态会先发生紊乱,再逐渐达到稳定,恢复为驼峰状;且峰值电流越大,耦合电弧形态紊乱越严重,达到稳定所需的时间越长。
图 5~图 7对应IP=70 A,
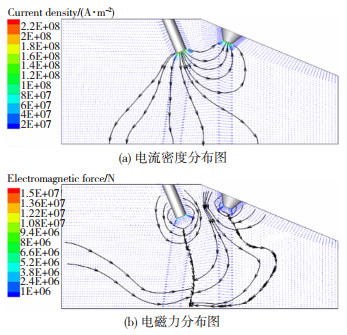
双弧脉冲MIG焊耦合电弧的特殊形态是由于主旁弧的电磁力不同造成的,图 8~图 10分别为不同主旁弧峰值电流达到稳态时的电流密度分布图和电磁力分布图。

|
图 8 IP=145 A, |
|
图 9 IP=70 A, |

|
图 10 IP=70 A, |
根据图 8(a)、图 9(a)、图 10(a)中电流密度分布所示,流经焊丝的电流密度分别流向工件表面和TIG焊枪,主旁弧产生的电磁力分布如图 8(b)、图 9(a)、图 10(b)所示。主旁弧的电磁力由四周指向中间,汇集到一条中心线,从而维持主旁弧的形态,但由于主旁弧的电流大小和方向不同,导致电磁力分布不对称。主弧受到自感应电磁力及旁弧洛伦兹力的耦合作用,沿焊丝轴线向左偏转。而根据电流密度分布图,可以发现主弧峰值电流越大,旁弧峰值电流越小,主弧电流密度向焊丝中心轴线左侧偏离的角度越小,因此,产生的电磁力越大,电磁力中心线向左偏转角度越小,从而使主弧向左偏转角度越小。而旁弧在自感应电磁力和主弧洛伦兹力的耦合作用下,向右偏转,旁弧峰值电流越大,主弧峰值电流越小,旁弧电流密度向钨极中心轴线右侧偏离的角度越大,因此,产生的电磁力越大,电磁力中心线向右偏转角度越大,从而使旁弧向右偏转角度越大。同时,越靠近工件表面,电流密度越小,产生的电磁力越小,主旁弧等离子流在电磁力的作用下运动,且随着电磁力中心线的偏转而偏转。当越靠近工件表面时,电磁力减小,导致电弧收缩量减小,同时等离子流在工件表面受到阻碍,向四周运动,从而导致耦合电弧形态的偏转和伸展,如图 3~图 7所示。当主弧峰值电流较大时,耦合电弧向钨极一侧伸展,而当旁弧峰值电流较大时,耦合电弧在工件表面向焊丝和钨极两侧进行伸展。
综上可知,通过调整主旁弧电流,可以调整耦合电弧达到相对稳定的时间及电磁力的分布,从而控制耦合电弧的稳定性和形态。
2.2 耦合电弧温度当脉冲电流发生跳变后,耦合电弧能够快速达到相对稳定的状态,本文主要对基值电流和峰值电流时达到相对稳定的耦合电弧,在yoz截面和z=0.1 mm水平截面的温度场进行分析。
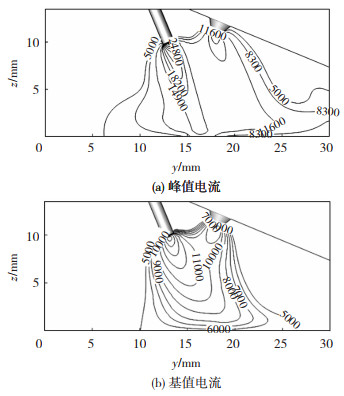
图 11~图 13是

|
图 11 IP=70 A, |

|
图 12 IP=145 A, |
|
图 13 IP=195 A, |
对比发现,当脉冲电流处于峰值时,耦合电弧温度场随主弧峰值电流变化明显。耦合电弧的热量主要来自焊丝和钨极产生的焦耳热,因此,峰值电流越大耦合电弧获得的焦耳热越多,其温度越高。由于只改变了主弧峰值电流,旁弧电流不变,因此,当处于峰值电流时,3组耦合电弧温度的变化主要表现在主弧一侧,当IP=70、145、195 A时,对应的主弧的最高温度约为26 000、30 000、32 000 K,旁弧的最高温度较为一致,约为19 000 K。且由于主弧峰值电流的增大,产生的电磁力增大,加速等离子流向工件表面运动,主弧温度场向工件方向伸展。对比不同峰值电流作用时的耦合电弧温度场发现,由于主旁弧等离子流在电磁力作用下发生偏转,使得耦合电弧整体温度场向钨极一侧偏移,且随着主弧峰值电流的增大,主弧向左偏转角度越小,温度场向钨极一侧偏移越多,这与耦合电弧形态的变化一致。
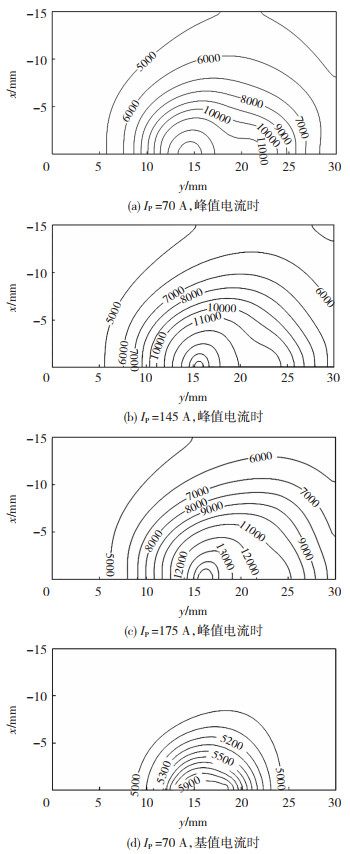
图 14是图 11~图 13中3组耦合电弧在z=0.1 mm水平截面的温度分布情况,图 14(a)~(c)对应3组脉冲电流峰值时期的耦合电弧,图 14(d)对应图 11中基值电流时的耦合电弧。从耦合电弧在yoz截面的温度场分布可以看出,当到达工件表面附近,耦合电弧的温度会发生急剧下降。由图 14(d)可以看出,当脉冲电流处于基值时,耦合电弧在水平截面的温度较低,分布范围较小。由图 14(a)~(c)可以看出,当处于峰值电流时,电磁力加速等离子流向工件方向运动,带给工件的热量增多,工件热输入增加,同时也使得耦合电弧在水平截面的分布范围扩大。当主弧峰值电流越大时,耦合电弧的整体温度越高,对工件热输入越高。同时由于耦合电弧的偏转,在z=0.1 mm水平截面的温度场同样偏向钨极一侧,主弧峰值电流越大,偏移越多。
|
图 14 z=0.1 mm水平截面温度场分布 Fig.14 Temperature field distribution in horizontal section with z=0.1 mm: (a) IP=70 A, peak current; (b) IP=145 A, peak current; (c) IP= 175 A, peak current; (d) IP=70 A, base current |
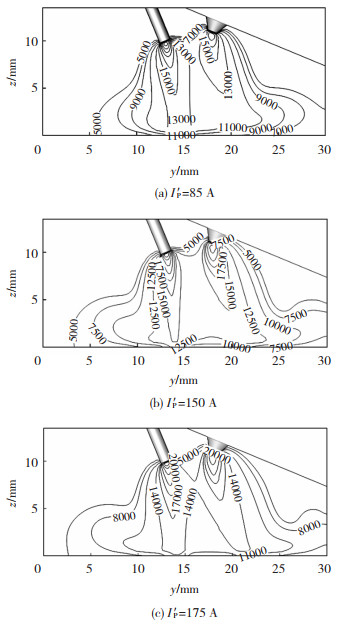
图 15为IP=70 A,
|
图 15 不同旁弧峰值电流时,耦合电弧温度场分布 Fig.15 Temperature field distribution of coupled arc under different side arc peak currents |
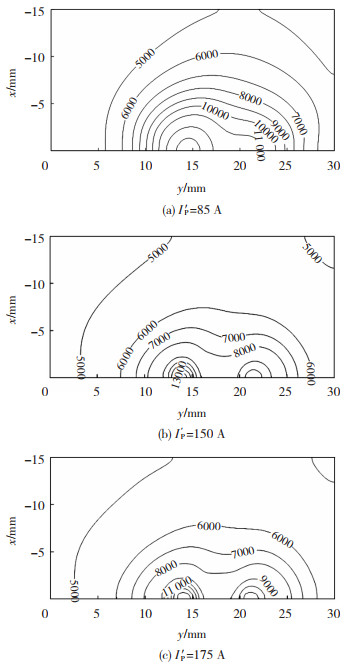
图 16是图 15中耦合电弧在z=0.1 mm水平截面的温度场分布。从图 15可以明显看出,当旁弧峰值电流越大时,耦合电弧在水平截面的分布范围越大,温度越高,对工件热输入越高。由于耦合电弧的整体温度场向钨极一侧偏转角度较小,导致水平截面上耦合电弧温度场向钨极一侧偏移较少。随着旁弧峰值电流的增加,由于旁弧等离子流受到电磁力增大,旁弧的温度场向工件方向伸展更多,当旁弧峰值电流过大时,水平表面的温度场开始呈现双峰分布。
|
图 16 z=0.1 mm水平截面温度场场分布 Fig.16 Temperature field distribution in horizontal section with z=0.1 mm |
图 17和图 18分别是不同主弧峰值电流和不同旁弧峰值电流时,z=0.1 mm截面中心线的温度(T)分布曲线。当焊接电流越大时,水平截面上耦合电弧的温度场分布范围越大,其温度越高。

|
图 17 不同主弧峰值电流时,z=0.1 mm水平截面中心线温度分布曲线 Fig.17 Temperature distribution curve of center line of horizontal section with z=0.1 mm under different main arc peak currents |
|
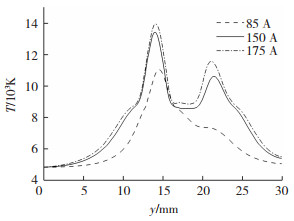
图 18 不同旁弧峰值电流时,z=0.1 mm水平截面中心线温度分布曲线 Fig.18 Temperature distribution curve of center line of horizontal section with z=0.1 mm under different side arc peak currents |
在图 17中,当IP=70、145、195 A时,z=0.1 mm水平截面的最高温度约为11 000、13 000、15 000 K。当主弧峰值电流增大时,由于温度场的偏移,温度峰值所在的位置逐渐向钨极一侧偏移,且电流越大,温度峰值所在的位置偏移越多。
而在图 18中,随着旁弧峰值电流的增大,水平截面的温度分布曲线开始呈现双峰分布,这与图 16中水平截面的温度场分布吻合。当
综上述分析,当脉冲电流增大时,耦合电弧温度升高,耦合电弧温度场向工件方向伸展,对工件的热输入增加,在工件表面的分布范围增大。对比5组脉冲电流作用下的耦合电弧温度可以发现,当焊丝总电流相同时,减小主弧电流,增大旁弧电流,主弧温度略有降低,但变化很小,而旁弧温度升高且变化较大,当旁弧峰值电流足够大时,z=0.1 mm水平截面的温度场呈双峰分布。
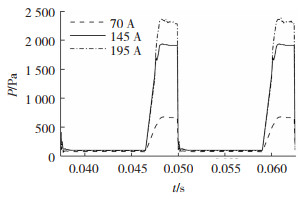
2.3 耦合电弧压力图 19是
|
图 19 不同主弧峰值电流时,电弧压力(P)随时间(t)的变化曲线 Fig.19 Arc pressure variation curve with time under different main arc peak currents |
如图 19所示,当脉冲电流发生跳变时,电弧压力发生变化,并逐渐趋于稳定,其变化滞后于脉冲电流的变化,且峰值电流越大,产生的电弧压力越大,达到稳定的时间越长。当脉冲电流处于基值电流时,由于电弧压力很小,约为100 Pa。当脉冲电流处于峰值时,相比于基值时耦合电弧压力较大,主弧峰值电流越大,电弧压力越大,当IP=70、145、195 A时,对应的电弧压力约为660、1 900、2 450 Pa, 随着主弧峰值电流的增大,电弧压力增幅减小。
图 20是IP=70 A,
|
图 20 不同旁弧峰值电流时, 电弧压力(P)随时间(t)的变化曲线 Fig.20 Arc pressure variation curve with time under different side arc peak currents |
通过对比5组脉冲电流作用下的电弧压力的变化规律,可以推断,当流经焊丝的总电流相同时,减小主弧电流、增大旁弧电流能够使主弧的电弧压力减小。
图 21为旁弧峰值电流为85 A,主弧峰值电流IP=70、145、195 A时,z=0.1 mm水平截面中心线的电弧压力分布。

|
图 21 不同主弧峰值电流时,z=0.1 mm水平截面中心线电弧压力分布曲线 Fig.21 Arc pressure distribution curve of center line of horizontal section with z=0.1 mm under different main arc peak currents |
由图 21可以看到,不同峰值电流下的电弧压力变化较大,主弧峰值电流为70、145、195 A时,对应最高电弧压力约为350、1 500、3 000 Pa,计算发现,当主弧峰值电流从70 A升高到145 A时,水平截面的耦合电弧温度变化率约为18.2%,而电弧压力的变化率约为328.6%,远高于电弧温度,因此,相对于耦合电弧的温度,电弧压力对脉冲电流的变化更为灵敏,这与文献[14]的结论一致。同时随着主弧峰值电流的增大,等离子流向钨极一侧偏转,导致电弧压力峰值向钨极一侧偏移,电流越大,偏移越多。因此,可以通过调整主旁弧的脉冲电流波形,控制焊接过程所需的电弧压力大小及作用范围,从而控制耦合电弧对熔池的作用力。
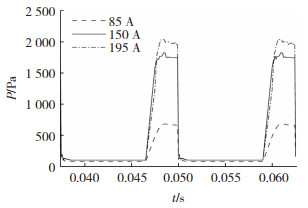
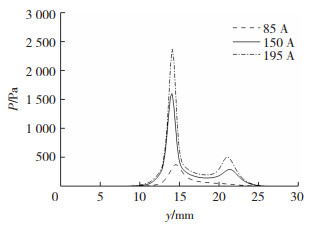
图 22为不同旁弧峰值电流时,z=0.1 mm水平截面中心线电弧压力分布曲线。与电弧温度分布类似,当旁路峰值电流足够大时,电弧压力呈现双峰分布。当旁弧峰值电流为85 A时,只有一个电弧压力峰值,约为370 Pa;当旁弧峰值电流为150、175 A时,电弧压力呈现双峰分布,对应的主弧一侧电弧压力峰值分别为1 600、2 400 Pa,旁弧一侧压力峰值较小,约为300、500 Pa。随着旁弧峰值电流的增大,受到电磁力影响,电弧压力的峰值位置向焊丝一侧偏移。
|
图 22 不同旁弧峰值电流时,z=0.1 mm水平截面中心线电弧压力分布曲线 Fig.22 Arc pressure distribution curve of center line of horizontal section with z=0.1 mm under different side arc peak currents |
在焊接过程中,熔池的形状取决电弧对其产生的作用力,其中电弧压力起重要作用,电弧压力过大,对熔池的作用力增强,容易造成未熔合、咬边、热裂纹等缺陷,电弧压力过小又会导致焊道两侧熔合。分析认为,电弧压力对脉冲电流的变化非常灵敏,焊接电流增大时,电弧压力增大,作用范围增大。对比5组脉冲电流作用下的电弧压力,当焊接总电流相同时,减小主弧电流,增大旁弧电流,主弧的电弧压力减小,而旁弧的电弧压力增大,当旁弧峰值电流足够大时,水平截面呈现双峰分布,使耦合电弧对熔池的作用范围增大。
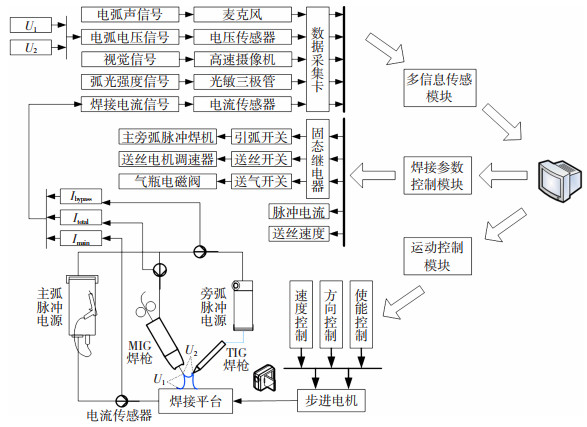
3 实验验证由于数值模拟过程中,进行了一系列简化与假设,因此需通过双弧脉冲MIG焊工艺实验验证数值模拟结果的准确性。为保证双弧脉冲MIG焊工艺实验的进行,搭建了基于LabVIEW的双弧脉冲MIG焊多信息传感控制系统,如图 23所示。
|
图 23 双弧脉冲MIG焊多信息传感控制系统 Fig.23 Multi-information sensing control system for dual-arc pulse MIG welding |
该系统主要包括多信息传感模块、焊接参数控制模块、运动控制模块,能够实现对焊接过程电压电流信号、视觉信号、声音信号以及弧光信号等多信息的实时采集和存储,以及对焊接过程的实时控制。
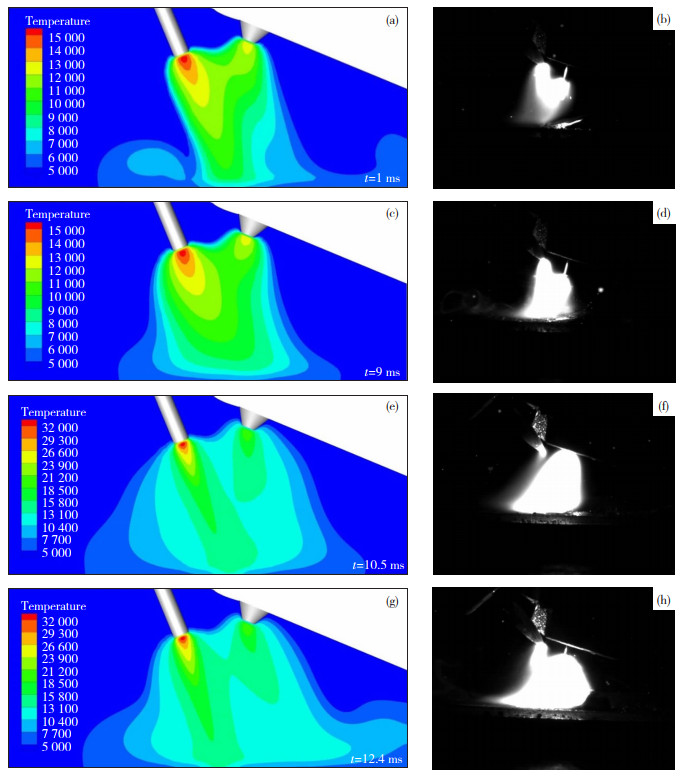
由于耦合电弧内部物理场较为复杂,且受实验设备限制,难以对其内部物理场进行实时监测,因此本文通过高速摄像机采集的焊接过程中耦合电弧图像来验证数值模拟结果的准确性。
焊接实验所采用的脉冲电流参数为:主旁弧电流选择同频脉冲电流,主弧峰值电流IP=70 A, 基值电流Ib=20 A,旁弧峰值电流
|
图 24 不同时刻下耦合电弧形态的数值模拟和实验结果对比 Fig.24 Comparison of numerical simulation and experimental results of coupled arc shape at different time points: (a), (b) t=1 ms; (c), (d) t=9 ms; (e), (f) t=10.5 ms; (g), (h) t=12.4 ms |
针对双弧脉冲MIG焊热源稳定性差、多参数匹配困难等问题,建立了双弧脉冲MIG焊耦合电弧三维模型,对5组不同脉冲电流参数作用下的耦合电弧进行瞬态数值模拟,并进行了实验验证。
1) 双弧脉冲MIG焊耦合电弧整体呈驼峰状,耦合电弧整体形态随主旁弧电流的变化而发生偏转,当主旁弧脉冲电流发生跳变时,耦合电弧形态发生伸展或收缩,最终达到相对稳定的状态,峰值电流越小,达到稳定的时间越短。
2) 当脉冲电流处于基值时,耦合电弧温度较低,仅起到维弧作用;当脉冲电流增大时,耦合电弧温度和电弧压力升高,工件的热输入增加,对熔池的作用力增大,作用范围增大。
3) 当总电流相同时,减小主弧电流,增大峰值电流,主弧温度和电弧压力减小,但变化较小,而旁弧温度和电弧压力增大。当旁弧电流足够大时,耦合电弧温度和电弧压力呈现双峰分布。
4) 搭建双弧脉冲MIG焊实验平台,通过焊接工艺试验对数值模拟结果进行了验证,数值模拟结果与双弧脉冲MIG焊工艺实验结果吻合良好,可对调控双弧脉冲MIG焊脉冲电流参数,改善其耦合电弧稳定性及工艺性能提供理论支持。
| [1] |
HONG K, SHIN Y. Prospects of laser welding technology in the automotive industry: Areview[J]. Journal of Materials Processing Technology, 2017, 465: 46-69. DOI:10.1016/j.jmatprotec.2017.02.008 |
| [2] |
QUAZI M M, ISHAK M, FAZAL M A, et al. Current research and development status of dissimilar materials laser welding of titanium and its alloys[J]. Optics and Laser Technology, 2020, 126(C): 106090. DOI:10.1016/j.optlastec.2020.106090 |
| [3] |
ZHANG Yan, GAO Yidi, ZHOU Jianping, et al. A composite joint based on two kinds of connection mechanisms for TA2/T2 bimetallic sheets by laser-TIG hybrid weldings[J]. Advances in Materials, 2020, 9(3): 55. DOI:10.11648/J.AM.20200903.13 |
| [4] |
CHEN Shuhai, LI Siqi, LI Yan, et al. Butt welding-brazing of steel to aluminum by hybrid laser CMT[J]. Journal of Materials Processing Technology, 2019, 272: 163-169. DOI:10.1016/j.jmatprotec.2019.05.018 |
| [5] |
TSUTOMU T, MASAYUKI N, SOHEI U, et al. Mechanism of intermetallic compound formation during the dissimilar friction stir welding of aluminum and steel[J]. Journal of Materials Science, 2020, 55(7): 1-9. DOI:10.1007/s10853-019-04106-2 |
| [6] |
MEHTA K P, CARLONE P, ASTARITA A, et al. Conventional and cooling assisted friction stir welding of AA6061 and AZ31B alloys[J]. Materials Science & Engineering A, 2019, 759: 252-261. DOI:10.1016/j.msea.2019.04.120 |
| [7] |
ZHANG Y M, JIANG M, LU W. Double Electrodes improve GMAW heat input control[J]. Welding Journal, 2004, 83(11): 39-41. |
| [8] |
李凯强. 双弧脉冲MIG焊过程稳定性分析及控制[D]. 曲阜: 曲阜师范大学, 2016. LI Kaiqiang. Stability analysis and control of double-arc pulse MIG welding process[D]. Qufu: Qufu Normal University, 2016. |
| [9] |
TOMASZ K. Heat source models in numerical simulations of laser welding[J]. Materials, 2020, 13(11): 2653. DOI:10.3390/ma13112653 |
| [10] |
AHMED H, CRISTINA C, MARÍA S J, et al. Experimental and numerical investigation of hybrid laser arc welding process and the influence of welding sequence on the manufacture of stiffened flat panels[J]. Journal of Manufacturing Processes, 2021, 61: 527-538. DOI:10.1016/j.jmapro.2020.11.040 |
| [11] |
BATAEV I A, TANAKA S, ZHOU Q D, et al. Towards better understanding of explosive welding by combination of numerical simulation and experimental study[J]. Materials & Design, 2019, 169: 107649. DOI:10.1016/j.matdes.2019.107649 |
| [12] |
IQBAL M P, TRIPATHI A, JAIN R, et al. Numerical modelling of microstructure in friction stir welding of aluminium alloys[J]. International Journal of Mechanical Sciences, 2020, 185: 105882. DOI:10.1016/j.ijmecsci.2020.105882 |
| [13] |
何俊杰, 马瑞杨, 王天琪. 镁合金冷金属过渡熔池动态行为数值模拟[J]. 材料科学与工艺, 2022, 30(5): 18-26. HE Junjie, MA Ruiyang, WANG Tianqi. Numerical simulation of dynamic behavior of magnesium alloy cold metal transition pool[J]. Materials Science and Technology, 2022, 30(5): 18-26. DOI:10.11951/j.issn.1005-0299.20210338 |
| [14] |
石玗, 郭朝博, 黄健康, 等. 脉冲电流作用下TIG电弧的数值分析[J]. 物理学报, 2011, 60(4): 738-744. SHI Yu, GUO Chaobo, HUANG Jiankang, et al. Numerical analysis of TIG arc under pulsed current[J]. Acta physica sinica, 2011, 60(4): 738-744. DOI: CNKI:SUN:WLXB.0.2011-04-119 |
| [15] |
OGINO Y, HIRATA Y, NOMURA K. Numerical analysis of the heat source characteristics of a two-electrode TIG arc[J]. Journal of Physics D Applied Physics, 2011, 44(21): 215202 (7pp). DOI:10.1088/0022-3727/44/21/215202 |
| [16] |
石玗, 韩日宏, 黄健康, 等. 旁路耦合电弧焊温度场模拟及验证[J]. 物理学报, 2012, 61(2): 23-29. SHI Yu, HAN Rihong, HUANG Jiankang, et al. Simulation and verification of temperature field in bypass coupled arc welding[J]. Acta physica sinica, 2012, 61(2): 23-29. DOI:10.7498/aps.61.020205 |
| [17] |
王新鑫, 樊丁, 黄健康, 等. 双钨极耦合电弧数值模拟[J]. 物理学报, 2013, 62(22): 412-421. WANG Xinxin, FAN Ding, HUANG Jiankang, et al. Numerical simulation of dual-tungsten coupled arc[J]. Acta Physica Sinica, 2013, 62(22): 412-421. DOI:10.7498/aps.62.228101 |
| [18] |
王新鑫, 樊丁, 黄健康, 等. 双钨极TIG电弧-熔池传热与流动数值模拟[J]. 金属学报, 2015, 51(2): 178-190. WANG Xinxin, FAN Ding, HUANG Jiankang, et al. Numerical simulation of heat transfer and fluid flow in double electrodes TIG arc-weld pool[J]. Acta Metallurgica Sinica, 2015, 51(2): 178-190. DOI:10.11900/0412.1961.2014.00401 |
| [19] |
ZONG Ran, CHEN Ji, WU Chuansong. A comparison of TIG-MIG hybrid welding with conventional MIG welding in the behaviors of arc, droplet and weld pool[J]. Journal of Materials Processing Technol, 2019, 270: 345-355. DOI:10.1016/j.jmatprotec.2019.03.003 |
| [20] |
FANG Naiwen, WANG Lliping, LI Liansheng, et al. Numerical simulation of DEGMAW of magnesium alloy cylinder[J]. China Welding, 2018, 27(2): 24-30. DOI:10.12073/j.cw.20180110001 |
| [21] |
FANG Naiwen, LI Liansheng, HUANG Ruisheng, et al. Effect of welding sequence on residual stress and deformation of Mg alloy fillet welds[J]. Journal of Physics, 2020, 1635: 17-19. DOI:10.1088/1742-6596/1635/1/012032 |
| [22] |
RODRÍGUEZ-HERNÁNDEZ T, CRUZ-HERNÁNDEZ V L, GARCÍA-RENTERÍA M A, et al. First assessment on the microstructure and mechanical properties of gtaw-gmaw hybrid welding of 6061-t6 AA[J]. Journal of Manufacturing Processes, 2020, 59: 658-667. DOI:10.1016/j.jmapro.2020.09.069 |
| [23] |
陈姬, 武传松, 陈茂爱. TIG-GAMW复合焊温度场的数值模拟[C]//中国焊接学会计算机辅助焊接工程专业委员会、哈尔滨工业大学先进焊接与连接国家重点实验室. 2014年全国计算机辅助焊接工程学术研讨会摘要集. 中国焊接学会计算机辅助焊接工程专业委员会、哈尔滨工业大学先进焊接与连接国家重点实验室: 中国焊接学会计算机辅助焊接工程专业委员会, 2014: 1. CHEN Ji, WU Chuansong, CHEN Maoai. Numerical Simulation of Temperature Field in TiG-GAMW Composite Welding[C]//Computer Aided Welding Engineering Committee of China Welding Society, State Key Laboratory of Advanced Welding and Joining, Harbin Institute of Technology. 2014 National Conference on Computer Aided Welding Engineering Abstract Collection. Computer Aided Welding Engineering Committee of China Welding Society, State Key Laboratory of Advanced Welding and Joining, Harbin Institute of Technology: Computer Aided Welding Engineering Committee of China Welding Society, 2014: 1. |
| [24] |
陈姬, 宗然, 武传松, 等. TIG-MIG复合焊电弧间相互作用对焊接过程的影响[J]. 机械工程学报, 2016, 52(6): 59-64. CHEN Ji, ZONG Ran, WU Chuansong, et al. Influence of arcs interaction on TIG-MIG hybrid welding process[J]. Journal of Mechanical Engineering, 2016, 52(6): 59-64. DOI:10.3901/JME.2016.06.059 |
| [25] |
HAN Yu, CHEN Ji, MA Haijun, et al. Numerical simulation of arc and droplet behaviors in TIG-MIG hybrid welding[J]. Journal of Mathematics, 2020, 13(20): 4520. DOI:10.3390/ma13204520 |
| [26] |
崔双双. TIG-MIG复合电弧-熔滴行为数值分析[D]. 济南: 山东大学, 2020. CUI Shuangshuang. Numerical analysis of TIG-MIG Composite arc-droplet behavior[D]. Ji'nan: Shandong University, 2020. |
| [27] |
PRAMOD R, KUMAR S M, GIRINATH B, et al. Fabrication, characterisation, and finite element analysis of cold metal transfer-based wire and arc additive-manufactured aluminium alloy 4043 cylinder[J]. Welding in the World, 2020, 64(11): 1905-1919. DOI:10.1007/s40194-020-00970-8 |
| [28] |
CHOO R T C, SZEKELY J, WESTHOFF R C. On the calculation of the free surface temperature of gas-tungsten-arc weld pools from first principles: Part I. modeling the welding arc[J]. Metallurgical Transactions B, 1992, 23(3): 357-369. DOI:10.1007/BF02656291 |
 2023, Vol. 31
2023, Vol. 31


