聚乳酸纳米纤维是最具发展前景的“绿色纤维”之一,因其良好的生物相容性和生物降解性在生物医用材料、过滤及防护、能源等领域具有广泛的应用[1]。静电纺丝技术作为目前唯一能够直接、连续制备聚合物纳米纤维的方法[2],所制备的纳米纤维具有表面积大、孔隙率高、直径小等优点[3]。然而静电纺丝工艺影响参数过多,会对纳米纤维的形态、孔隙率等产生影响,进一步影响到纤维膜过滤效率和过滤阻力[4]。在其制备过程中,为了得到所需的纳米纤维膜,需要花费大量的时间确定合适的工艺参数,导致制备效率较低。此外,由于静电纺丝工艺参数与纳米纤维直径、孔隙率等性能指标间的非线性关系,很难建立确切的数学模型,导致静电纺丝工艺参数方面的研究比较欠缺[5]。因此优化工艺参数对于提升静电纺丝制备纳米纤维效率和规模化生产具有十分重要的意义。
目前,国内外学者主要研究静电纺丝工艺参数对纳米纤维直径及性能的影响。聂孙建等[6]研究了纺丝液浓度对纳米纤维直径和表面形貌的影响,但是在对静电纺丝工艺参数的优化上并没有过多关注。Doustgani等[7]采用正交试验法对聚乳酸纳米纤维熔体静电纺丝工艺参数进行了优化。陈思羽等[8]提出了均匀设计法,并进行多因素多水平的实验设计优化静电纺丝工艺参数,最终实现了对纤维直径的有效预测。然而,尽管利用传统的数学统计分析方法建立了一定的数学回归方程,但是其具有计算开销大的问题,在规模化生产中难以应用[7-8]。有学者基于响应面法建立了相应的预测模型对静电纺丝工艺参数优化[9-12],该方法仅利用较少的实验,就能在局部范围内建立函数模型,且代数表达式建立简单,但是响应面法不能保证通过所有的样本点,在预测上存在一定的误差。传统的优化静电纺丝工艺参数的方法难以满足实际需求,需要寻找新型的工艺参数优化方法。
神经网络是近年来快速发展的人工智能的一个重要部分。作为一种非线性数据建模工具,神经网络能快速找出输入参数与输出参数间的函数关系[13]。因此,利用神经网络优化静电纺丝工艺逐渐引起学者的关注。其中,BP(Back Propagation)和RBF(Radial Basis Function)神经网络是目前应用较广的两种神经网络。BP网络是一种按误差反向传播训练的多层前馈网络,由输入层、隐藏层和输出层构成[14]。反向传播中,通过对权值和偏移量的不断修改,使网络的实际输出更接近于期望输出[15]。权值和偏移量的调节对BP网络的输出均有影响,因此BP神经网络是对非线性映射的“全局逼近”[16]。RBF神经网络与BP神经网络结构类似,但其以径向基函数作为隐藏层神经元激活函数[17],输入参数直接映射到隐藏层,无需权值连接。从输入层到隐藏层的变换是非线性的,从隐藏层到输出层的变换是线性的[18]。RBF网络的输出只与部分调节参数有关,因此具有“局部映射”特性。
利用BP神经网络算法构建预测模型,可得到静电纺丝工艺参数与纳米纤维膜性能指标的关系式[14-16]。采用响应面法和人工神经网络算法(ANN)分别对输入因子进行预测[19-20],发现神经网络对于高度复杂的数学模型拟合效果较好,准确性更高。
针对上述问题,本文在文献[14-16]的研究基础上,以聚乳酸纳米纤维膜为研究对象,采用纳米纤维直径为性能评价指标,通过设计实验获得数据样本,利用BP误差反向传播和RBF径向基神经网络搭建静电纺丝工艺参数与纤维直径的预测模型。对预测结果进行对比分析,选出预测精度更高、效果更好的方法,从而优化静电纺丝工艺参数,提升纳米纤维制备效率。
1 实验 1.1 材料及设备左旋聚乳酸(PLLA),相对分子质量1.43×106,PURAC Biomaterials;N, N-二甲基甲酰胺(DMF,分析纯),二氯甲烷(DCM,分析纯),上海阿拉丁生化科技股份有限公司。
NS-1专业型静电纺丝设备(青岛聚纳达科技有限公司);DF101S型磁力搅拌器(秋佐科技)。
1.2 纺丝液制备以PLLA为溶质,以DCM和DMF(质量比为19:1)的混合液为纺丝溶剂。首先将PLLA颗粒加入装有DCM液体的广口瓶中。密封后置于磁力搅拌器中,50 ℃下搅拌加热,直到溶液变得透明,然后缓慢将DMF加到溶液中,进行搅拌,配置PLLA质量分数为1.8%~2.2%的纺丝液。
1.3 纤维膜制备将制备好的聚乳酸纺丝液转移到5 mL的注射器中,针头大小为20G,将注射器固定在静电纺丝机注射泵上,调整高度使其与滚筒接收器中心位于同一水平线。静电纺丝操作在室温((25±2) ℃) 下进行,滚筒转速为100 r/min,设置好高压电源输出电压,调整针头与滚筒接收器间的距离,开始制备聚乳酸纳米纤维膜。实验用到的设备和制备过程如图 1所示。

|
图 1 静电纺丝设备(a)与纳米纤维制备(b) Fig.1 Electrospinning device (a) and preparation of nanofibers (b) |
对静电纺丝制备的纳米纤维膜进行形态表征的目的是测量制备样品的纤维直径。由于纤维直径是纳米纤维膜的性能评价指标,因此被用作预测模型的输出层节点。在后续实验设计中制备不同工艺参数下的纳米纤维膜,通过对不同纳米纤维膜进行形态表征以及利用ImageJ软件测量即可获得纤维平均直径。具体操作如下:对制备好的聚乳酸纳米纤维膜表面进行喷金处理,采用高分辨率场发射扫描电子显微镜(JSM-7900F,日本JEOL公司) 观察纤维表面形貌,如图 2所示。利用ImageJ软件测量纤维直径,为了避免偶然性,在图 2中随机选取样品N个区域测量纤维直径,并计算出纤维平均直径。

|
图 2 PLLA纤维膜SEM形貌 Fig.2 SEM morphology of PLLA fiber membrane |
为了保证实验的效能性且充分考察聚合物含量、电压、推进速度和接收距离对纤维直径的影响,以聚合物含量、电压、推进速度和接收距离作为输入变量,设定PLLA含量为1.8%~2.2%;电压18~22 kV;推进速度0.6~1.0 mm/min;接收距离13~17 cm。选取的4因素5水平编码,如表 1所示。采用ImageJ软件测得的聚乳酸纳米纤维平均直径作为性能评价指标,采取单因素控制变量法研究工艺参数对纤维直径的影响,设计20组实验作为训练样本,如表 2所示。考虑到实验的一般性原则,再设计8组实验作为测试验证,如表 3所示。
| 表 1 工艺参数因素编码水平表 Table 1 Process parameter factor coding level |
| 表 2 训练样本 Table 2 Training samples |
| 表 3 测试样本 Table 3 Testing samples |
采用三层BP神经网络建立预测模型,以聚合物含量、电压、推进速度和接收距离作为输入变量,以纤维直径作为输出结果。因此构建的神经网络模型在输入层为4个节点,在输出层有1个节点。隐藏层的节点个数是影响BP神经网络模型的关键因素之一,如果隐藏层节点过多,会增加网络训练时间,在训练过程中容易出现过拟合;如果隐藏层节点数较少,则神经元训练不足,无法达到网络的预期目标。本研究以误差均方值为目标,隐藏层神经元的最优个数主要通过试错得到。经过反复训练,当隐藏层节点数为4时,误差均方值最小,BP神经网络预测性能最佳。
使用实验测得的28组数据样本进行分析,对数据进行归一化处理,使模型样本数据处于[0, 1]之间,所用函数为
| $ x_i=\left(x-x_{i, \min }\right) /\left(x_{i, \max }-x_{i, \min }\right) $ | (1) |
式中:xi为归一化后的数据;xi, min和xi, max分别为数据中最小和最大的数。实验数据中训练样本用于搭建预测模型,测试样本用于衡量模型的泛化能力。隐藏层传递函数选择“tansig”、“purelin”,训练函数选择“trainlm”函数,使用newff函数建立神经网络模型。设置最大训练次数为400,均方误差目标为0.001,学习速率为0.05,对模型进行训练测试得到预测结果。
2.2 RBF神经网络的构建利用RBF神经网络对28组数据进行归一化处理后建立预测模型,输入层节点、输出层节点与BP神经网络设置相同,隐藏层节点数经过反复测试发现当神经元个数为25时达到了较好的逼近效果。使用“newrb”函数建立神经网络模型。在RBF神经网络模型中,扩展系数对RBF模型预测性能起着决定性影响,经过反复测试,将其设置为12,设置均方误差目标为0.001,对实验数据进行训练测试。
3 神经网络预测结果与分析为了验证BP和RBF神经网络模型的预测性能,对两种网络模型拟合度进行比较,得出样本值与模型训练输出值在训练样本和测试样本上的拟合回归情况,如图 3所示。

|
图 3 BP和RBF神经网络模型性能预测拟合曲线 Fig.3 Fitting curves of performance prediction by BP and RBF neural networks: (a) training samples of BP network; (b) testing samples of BP network; (c) training samples of RBF network; (d) testing samples of RBF network |
可以看出两种网络模型在训练样本上的拟合程度都比较高,拟合相关系数均达到了0.99。当样本归一化值与模型训练值相等,即拟合直线Y=T时,拟合相关系数R值为1。R值越接近1,表明实际输出与期望输出间的相关性越高。在测试样本上,BP神经网络模型的拟合相关系数为0.942 98,预测输出与目标输出有一定的偏差,RBF神经网络模型为0.991 71。综上分析可知,两种网络模型都具有较好的预测能力,RBF神经网络的预测性能更优越,对输入样本具有更准确的预测能力。
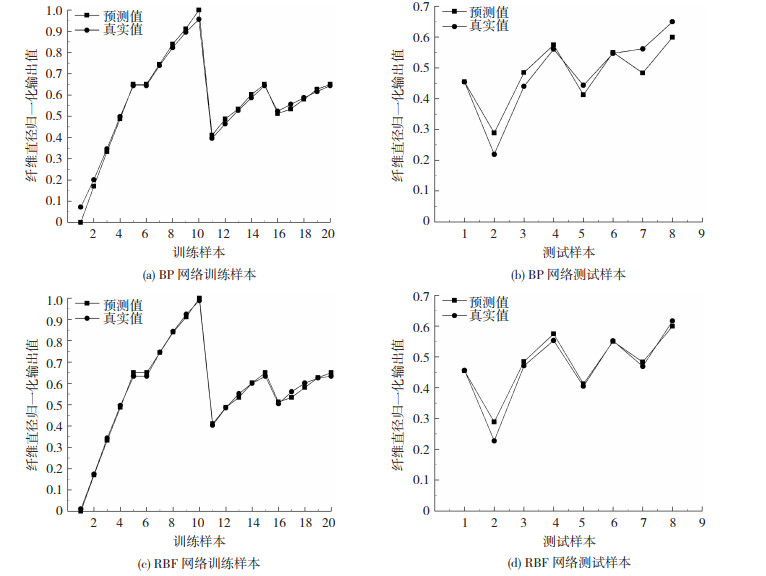
为了进一步验证预测性能,通过建立好的BP和RBF神经网络模型对纤维直径进行结果预测,得出分别针对训练样本和测试样本上的纤维直径归一化输出值,如图 4所示。针对训练样本,BP和RBF构建的网络模型预测值与真实值基本吻合,两种神经网络模型都很好地完成了对样本的最佳逼近。针对测试样本,尽管和预测样本有一定误差,但是总体预测效果较好,实现了对纤维直径在可接受误差范围内的预测。由图可以看出,BP神经网络仅在第4组测试样本预测精度较高,预测结果优于RBF神经网络,在其他组测试样本上均低于RBF神经网络。
|
图 4 BP和RBF神经网络对纤维直径的预测曲线 Fig.4 Prediction curve of fiber diameter by BP and RBF neural networks: (a) training samples of BP network; (b)testing samples of BP network; (c)training samples of RBF network; (d)testing samples of RBF network |
神经网络模型的预测误差表明了模型的精度。为了更直观表现测试样本中预测值与真实值的偏差,通过反归一化函数还原数据原始数量级,并计算两种网络预测模型的预测误差和相对误差。
| $ \begin{gathered} \text { Error }=R_i-P_i \end{gathered} $ | (2) |
| $ \text { Relative error }=\frac{R_i-P_i}{R_i} $ | (3) |
式中:Ri为真实值;Pi为预测值。
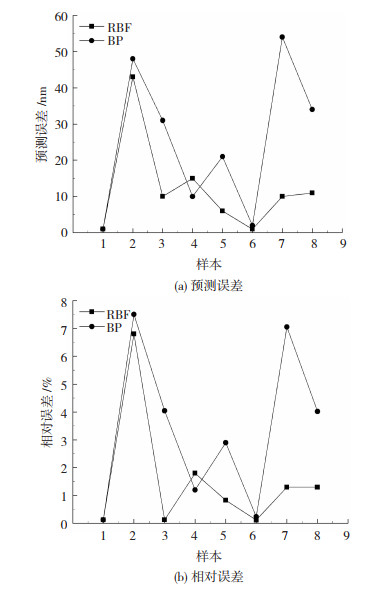
从图 5可以看出,BP神经网络模型的预测误差在0~60 nm,最大误差54 nm,相对误差不超过8%;RBF神经网络模型的预测误差在0~45 nm,最大误差为43 nm,相对误差不超过7%。BP和RBF神经网络均在测试样本第2组实验数据表现出较大误差。在其他组测试数据,RBF神经网络预测误差在1~15 nm,预测性能明显优于BP神经网络。可见,RBF模型比BP模型预测精度更高,稳定性更好。
|
图 5 BP与RBF神经网络模型误差分析 Fig.5 Error analysis of BP and RBF neural networks: (a)prediction error; (b)relative error |
对预测值与真实值进行分析,使用平均绝对误差(MAE)衡量预测模型准确性。BP模型训练样本平均绝对误差为12.3 nm,测试样本为25.125 nm;RBF模型训练样本平均绝对误差为7.4 nm,测试样本为12.125 nm,两种模型均表现出优异的预测性能。RBF模型在训练样本和测试样本上的平均绝对误差均小于BP模型,且RBF模型在训练样本和测试样本间的偏差更小,说明RBF神经网络模型表现出更好的泛化能力和预测效果。
4 结论利用静电纺丝工艺参数与纳米纤维直径相关性建立数学预测模型,从而优化静电纺丝制备工艺,具有重要的实际应用价值。利用神经网络在预测领域的优异性能,本文通过RBF神经网络和BP神经网络建立预测模型,对模型进行分析得出结论如下:
1) 在同等条件下使用RBF神经网络和BP神经网络建立的预测模型,拟合相关系数较高,两种神经网络均能较好的预测不同工艺参数下的纤维直径,能为静电纺丝制备过程中工艺参数的选择提供依据。
2) 将RBF神经网络预测模型与BP神经网络进行对比发现:RBF神经网络有着更高的预测精度,训练样本平均绝对误差为7.4 nm,测试样本平均绝对误差为12.125 nm,相对误差不超过7%,模型泛化能力更好,训练更加稳定,预测效果更好。
| [1] |
ABDULKHANI A, HOSSEINZADEH J, ASHORI A, et al. Preparation and characterization of modified cellulose nanofibersreinforced polylactic acid nanocomposite[J]. Polymer Testing, 2014, 35: 73-79. DOI:10.1016/j.polymertesting.2014.03.002 |
| [2] |
杨恩龙, 王善元, 李妮, 等. 静电纺丝技术及其研究进展[J]. 产业用纺织品, 2007(8): 7-10, 14. YANG Enlong, WANG Shanyuan, LI Ni, et al. Process inresearch of electrospinning technique[J]. Technical Textiles, 2007(8): 7-10, 14. DOI:10.3969/j.issn.1004-7093.2007.08.002 |
| [3] |
王雪芳, 刘景艳, 王鸿博, 等. 聚乳酸纳米纤维的电纺制备及影响因素[J]. 高分子材料科学与工程, 2014, 30(8): 161-166. WANG Xuefang, LIU Jingyan, WANG Hongbo, et al. Influencing factors of preparation of polylactic acid nanofibervia electrospinning[J]. Polymer Materials Science & Engineering, 2014, 30(8): 161-166. DOI:10.16865/j.cnki.1000-7555.2014.08.032 |
| [4] |
王银利, 陈艳, 张晓静, 等. 静电纺参数对二醋酸纳米纤维直径分布的影响[J]. 纺织学报, 2010, 31(11): 6-10. WANG Yinli, CHEN Yan, ZHANG Xiaojing, et al. Effect of electrospinningparameters on diameter distribution of SCA nanofiber[J]. Journal of Textile Research, 2010, 31(11): 6-10. DOI:10.13475/j.fzxb.2010.11.001 |
| [5] |
汪成伟. 基于静电纺丝技术的纳米纤维制备工艺及其应用研究[D]. 苏州: 苏州大学, 2016. WANG Chengwei. Preparation and application of nanofibersbased on electrostatic spinning technology[D]. Shuzhou: Soochow University, 2016. |
| [6] |
聂孙建, 梁燕, 周冠辰, 等. 静电纺PA66纳米纤维的制备与工艺研究[J]. 纺织科技进展, 2021(3): 14-17, 25. NIE Sunjian, LIANG Yan, ZHOU Guanchen, et al. Study on preparation and process of electrospinning PA66 nanofiber[J]. Progress in Textile Science & Technology, 2021(3): 14-17, 25. DOI:10.19507/j.cnki.1673-0356.2021.03.004 |
| [7] |
DOUSTGANI A, AHMADI E. Melt electrospinning process optimization of polylactic acid nanofibers[J]. Journal of Industrial Textiles, 2016, 45(4): 626-634. DOI:10.1177/1528083715610297 |
| [8] |
陈思羽, 吴春林, 王贺云, 等. 均匀设计法优化PVC静电纺丝工艺参数[J]. 石河子大学学报(自然科学版), 2015, 33(6): 766-774. CHEN Siyu, WU Chunlin, WANG Heyun, et al. Optimize the process parameters on the electrospinning of polyvinylchloride by uniform design method[J]. Journal of Shihezi University(Natural Science), 2015, 33(6): 766-774. DOI:10.13880/j.cnki.65-1174/n.2015.06.020 |
| [9] |
KHAN A N, GOUD V, ALAGIRUSAMY R, et al. Optimization study on wet electrostatic powder coating process to manufacture UHMWPE/LDPE towpregs[J]. Journal of Industrial Textiles, 2022, 51(S4): 6686-6704. DOI:10.1177/15280837211070995 |
| [10] |
赵鹏程, 王俊元, 梅林玉, 等. 基于响应面法的静电纺丝制备壳聚糖/聚氧化乙烯的工艺参数优化[J]. 丝绸, 2020, 57(2): 31-34. ZHAO Pengcheng, WANG Junyuan, MEI Linyu, et al. Optimization of process parameters for preparation of CS /PEO by electrospinningbased on responsesurface methodology[J]. Journal of Silk, 2020, 57(2): 31-34. DOI:10.3969/j.issn.1001-7003.2020.02.006 |
| [11] |
魏娜, 孙诚, 王丽超, 等. 静电纺羧甲基壳聚糖纳米纤维直径的预测模型[J]. 包装工程, 2016, 37(13): 8-13. WEI Na, SUN Cheng, WANG Lichao, et al. Prediction model of the diameter of carboxymethyl chitosam nanofibers prepared by electrospinning[J]. Packaging Engineering, 2016, 37(13): 8-13. DOI:10.19554/j.cnki.1001-3563.2016.13.002 |
| [12] |
CHEN P, ZHOU Q H, CHEN G, et al. Prediction and optimization of process parameters of electrospun polyacrylonitrile based on numerical simulation and responsesurface method[J]. Textile Research Journal, 2021, 91(19-20): 2332-2344. DOI:10.1177/00405175211003986 |
| [13] |
彭彬彬, 闫献国, 杜娟. 基于BP和RBF神经网络的表面质量预测研究[J]. 表面技术, 2020, 49(10): 324-328, 337. PENG Binbin, YAN Xianguo, DU Juan. Surface quality prediction based on BP and RBF neural networks[J]. Surface Technology, 2020, 49(10): 324-328, 337. DOI:10.16490/j.cnki.issn.1001-3660.2020.10.038 |
| [14] |
王婷. 静电纺纳米纤维膜孔隙率的数学模型及分形性质的研究[D]. 天津: 天津工业大学, 2019. WANG Ting. Study on mathematical model and fractal properties of porosity of electrospun nanofiber membrane[D]. Tianjin: Tiangong University, 2019. |
| [15] |
KANG L, LIU Y K, WANG L P, et al. Preparation of electrospun nanofiber membrane for air filtration and process optimization based on BP neural network[J]. Materials Research Express, 2021, 8(11): 115010. DOI:10.1088/2053-1591/ac37d6 |
| [16] |
康乐, 王立志, 高晓平. 基于BP神经网络的聚偏氟乙烯/聚丙烯梯度复合滤料工艺优化[J]. 复合材料学报, 2022, 39(8): 3776-3785. KANG Le, WANG Lizhi, GAO Xiaoping. Process optimization of polyvinylidene fluoride/polypropylene gradient composite filter material based on BP neural network[J]. Acta Materiae Compositae Sinica, 2022, 39(8): 3776-3785. DOI:10.13801/j.cnki.fhclxb.20210913.005 |
| [17] |
周金华, 任军学, 蔡菊. 基于RBF神经网络的航空叶片铣削残余应力预测[J]. 计算机集成制造系统, 2018, 24(2): 361-370. ZHOU Jinhua, REN Junxue, CAI Ju. Prediction of milling residual stress of aviation blade based on RBF neural network[J]. Computer Integrated Manufacturing Systems, 2018, 24(2): 361-370. DOI:10.13196/j.cims.2018.02.008 |
| [18] |
TAO J, YU Z, ZHANG R, et al. RBF neural network modeling approach using PCA based LM-GA optimization for coke furnace system[J]. Applied Soft Computing, 2021, 111: 1076. |
| [19] |
KHANLOU H M, SADOLLAH A, ANG B C, et al. Prediction and optimization of electrospinning parameters forpolymethyl methacrylate nanofiber fabrication using response surface methodology and artificial neural networks[J]. Neural Computing and Applications, 2014, 25(3): 767-777. DOI:10.1007/s00521-014-1554-8 |
| [20] |
NASOURI K, BAHRAMBEYGI H, RABBI A, et al. Modeling and optimization of electrospun PAN nanofiber diameterusing response surface methodology and artificial neural networks[J]. Journal of Applied Polymer Science, 2012, 126(1): 127-135. |
 2023, Vol. 31
2023, Vol. 31


