2. 中国石油集团工程技术研究有限公司,天津 300451
2. CNPC Engineering Technology Research Co., Ltd., Tianjin 300451, China
在船舶、工业锅炉等大型机械中,中厚板焊接具有较多的应用[1-3]。中厚板V型坡口多层多道焊接时,多层多道焊道的堆积会引起每层焊道之间因误差累积导致的质量问题,一般通过调节焊接工艺参数改变焊道几何形态从而提高焊缝成形质量。但因多层多道焊接时每一条焊道初始条件不同,根据现有工艺库很难直接获得预期尺寸的焊道,因此焊道几何参数预测对成形质量预测[4-5]以及成形质量控制[6-9]都有较大意义。
在多层多道焊接过程中,焊接工艺参数作为外部输入直接影响焊接质量,熔池的状态特征能直接反映焊接质量、焊接缺陷以及焊道形态。Zhu等[10]针对窄间隙气体保护焊容易产生气孔、未熔合缺陷的问题,采用三维瞬态数值模拟方法,研究了熔池行为及其对焊接缺陷的影响,发现靠近熔池侧壁边界的向上流动会造成未熔合缺陷,而靠近侧壁的向下和向后流动可能导致气孔。王建军等[11]通过分析铝合金焊接过程的特点,建立了焊接参数与熔池几何参数之间的随机系统模型,设计了基于电流最小方差调节的焊缝熔宽自适应控制器。
焊接是一个非线性、瞬时的过程,因此很难使用传统方法建立高精度的数学模型。神经网络可以在不考虑其他外界因素的情况下实现建模和预测,使用神经网络预测焊道几何参数能实现较好的效果[12-16]。Li等[17]通过瞬态响应实验验证了在其它焊接工艺参数不变的情况下,焊接速度的变化对焊道截面几何特征有直接影响,建立了以焊接速度为输入,焊缝宽度和高度为输出的人工神经网络模型,用于预测焊接速度变化时的焊道截面几何特征。高进强等[18]通过CCD相机获得熔池正面图像,经过图像处理算法得到熔池正面几何尺寸,通过BP神经网络搭建了熔池正面几何参数与背面熔宽的关系模型,实现了对背面熔宽的控制。
BP神经网络具有非线性映射能力、自适应能力和自学习能力强等优势,文中以BP神经网络[19]模型为基础对V型坡口焊道几何参数进行预测,分析各焊接工艺参数对焊道形态的影响,确定了神经网络的输入输出参数。但BP神经网络存在易陷入局部极值、收敛速度慢的问题。麻雀搜索算法(SSA)[20]具有寻优能力强、收敛速度快的优势,为进一步提高模型的稳定性和精度,引入麻雀搜索算法对模型进行优化。对比优化前后模型性能,优化后的模型满足V型坡口焊道几何参数预测精度要求。
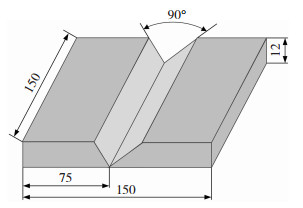
1 实验 1.1 V型坡口焊接视觉传感实验系统平台如图 1所示,实验系统主要由工业机器人(ABB-IRB14 10)、Fronius TPS 4000 CMT自动化焊机(一元化焊接工艺)执行焊接工作,使用XVC-1000摄像机进行熔池图像连续采集。图 2为待焊工件参数,工件选用Q235低碳钢,规格为150 mm×75 mm×12 mm,坡口角度为90°,焊丝采用1.2 mm直径实心焊丝THQ-50C。

|
图 1 V型坡口焊接视觉传感实验系统平台 Fig.1 Visual sensing test system platform of V-bevel welding |
|
图 2 待焊工件(单位:mm) Fig.2 Work piece to be welded |
在对待焊工件进行多层多道焊接时,完成打底焊后,让后续的每一焊层都比前一焊层多一条焊道,从左到右依次焊接,如图 3所示,待每条焊道冷却后测量获得所需的宏观尺寸数据,在该焊接过程下验证采用SSA优化的BP神经网络预测模型的可行性和准确性。
|
图 3 焊接工艺 Fig.3 Welding process |
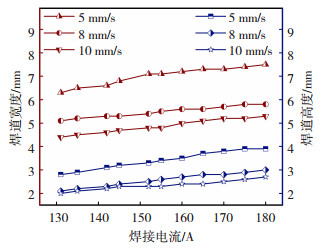
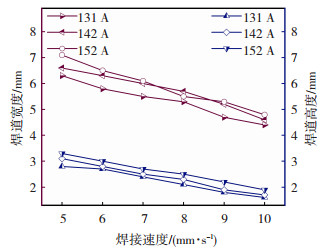
图 4为采用不同焊接电流和不同焊接速度进行的单道焊接对比实验,用于分析焊道宽度和高度与参数关系。如图 5所示,其它参数不变,随着焊接电流的增加焊道宽度和高度增加;如图 6所示,随着焊接速度的增加焊道宽度和高度随之减小。这是因为焊接电流与单位时间熔覆金属量成正比,焊接速度与焊接时间成反比,两者共同作用决定了焊道的熔覆体积。

|
图 4 对比实验 Fig.4 Comparative experiment |
|
图 5 焊接电流对焊道宽度和高度的影响 Fig.5 Effect of welding current on width and height of weld channel |
|
图 6 焊接速度对焊道宽度和高度的影响 Fig.6 Effect of welding speed on width and height of weld channel |
建立焊道几何参数预测模型首先要选择合理的输入和输出,根据焊接工艺参数对焊道形态的影响以及对图 5、6中的数据分析得出:在调整焊接工艺参数的过程中,焊接电流和焊接速度对焊道几何参数都有直接影响,可作为模型的输入参数。
多层多道焊接时,每一条焊道都受到前一道和前一层焊道的影响,焊道间隙和不平整的焊道表面会导致电弧偏转及弧长变化,造成焊道尺寸与预期存在偏差。焊接所形成的熔池是焊接工艺参数在当前焊接点热传导和热累积的直接反映,包含了能反映焊接过程和焊接质量的丰富信息。在输入参数中加入熔池特征,可以综合考虑焊道间隙、弧长变化等因素的影响,图 7为熔池信息。

|
图 7 熔池宽度 Fig.7 Melt pool width |
由于V型坡口多层多道焊接过程复杂,多层焊道之间的误差累积后,会出现如图 8所示的最上层焊道表面不平整的典型问题。为了避免这种问题,需要对焊接过程中每条焊道的几何参数进行预测。为准确可靠地预测焊道参数,确定以焊接工艺参数(焊接电流I、焊接速度v)和熔池宽度W作为神经网络的输入,将能表征焊接质量的单道焊道高度h1和焊道计算高度h2作为输出。熔池宽度为焊接过程中随机测量5张熔池图像的均值。焊道高度为焊道截面最低点到顶端垂直投影距离,焊道计算高度为焊道截面最低点到顶部搭接一侧最低点垂直投影距离,如图 9所示。

|
图 8 不平整的焊缝表面 Fig.8 Uneven weld surface |

|
图 9 焊道特征尺寸示意图 Fig.9 Schematic diagram of weld channel feature size |
目前的相关研究中,通过增加隐藏层数量或增加隐藏层节点数量来提高预测精度的有效性还没有得到证实,但这样会使神经网络更复杂,模型的训练时间更长、占用空间更大。实际计算中常选择具有单个隐藏层的三层网络。隐藏层节点数的选择对神经网络模型的性能也有很大影响,综合考虑网络结构的复杂性、误差的大小和样本数,以及对性能的比较,确定了隐藏层节点数为4。综上,已经可以确定用于预测V型坡口焊道几何参数的BP神经网络模型,模型结构如图 10所示。
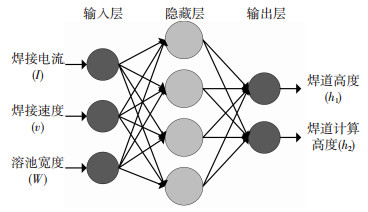
|
图 10 BP神经网络模型结构 Fig.10 BP neural network model structure |
训练样本数量需要满足大于预测模型连接权重数量的要求,因此,本文中至少需要40个训练样本。采用同一组打底焊接参数获得实验预制件,在此基础上进行填充层焊接,测量焊接成形较好工件填充层每条焊道,共测得60组焊道宏观尺寸,其中50组作为训练样本,10组作为测试样本,表 1为部分样本数据。BP神经网络训练参数设置为:训练次数1 000次;学习率0.01;目标误差0.000 1。
| 表 1 部分样本数据 Table 1 Partial sample data |
图 11为测试集预测结果与实际结果的比较,图 12为训练效果较好的10组计算均方根误差,从中可得到焊道高度和焊道计算高度预测结果的最大误差为0.2 mm,最大均方根误差差值为0.1 mm。结果表明,该模型理论上能够一定程度的预测焊道成形尺寸,但是测试集的预测精度和稳定性不能满足焊道成形质量评估标准,较大的误差会造成计算机误判从而引起错误的机器人指令,造成更严重的问题。因此,为提高V型坡口焊道几何参数预测模型的性能,需要对模型进行优化。
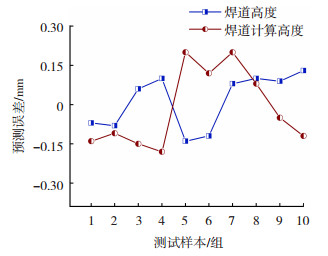
|
图 11 优化前模型预测误差 Fig.11 Model prediction error before optimization |
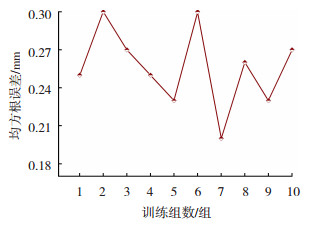
|
图 12 优化前模型均方根误差 Fig.12 RMSE of model before optimization |
由于BP神经网络初始连接权值和阈值的选择对训练结果的影响很大,网络训练时容易过早陷入局部最小点,针对这些问题可以采用麻雀搜索算法优化BP神经网络的初始权值、阈值,达到提高模型训练速度、预测精度以及稳定性的目的。图 13为SSA-BP算法流程图。
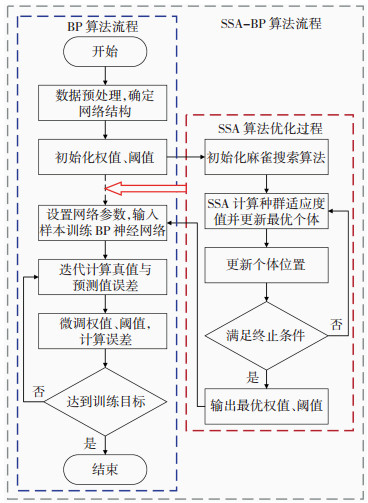
|
图 13 SSA-BP算法流程图 Fig.13 Flow chart of SSA-BP algorithm |
该优化算法受麻雀觅食和反捕食行为的启发,将麻雀种群分为发现者和加入者,分别负责提供种群觅食方向和获取食物。当种群中的侦查者觉察到危险时,种群移动到安全区域觅食并更新种群位置。该算法在每次迭代过程中,发现者的位置更新可由公式(1)获得:R2<ST时,表示周围觅食环境安全,发现者可以前往更广泛的区域发现食物;R2≥ST时,表示部分麻雀发现捕食者并报警,种群前往更安全的区域觅食。
| $ X_{i, j}^{t+1}=\left\{\begin{array}{l} X_{i, j}^t \cdot \exp \left(\frac{-i}{a \cdot N}\right), R_2<S T \\ X_{i, j}^t+Q \cdot L \quad, R_2 \geqslant S T \end{array}\right. $ | (1) |
式中:Xi, j为第i只麻雀在第j维中的位置;t为当前迭代次数;N为最大迭代次数;n为种群大小;ST为安全值,ST∈[0.5, 1];R2为预警值,R2∈[0, 1];Q为服从正太分布的随机数;L为单位行向量;a为(0, 1]之间的随机数。
加入者的位置更新可由公式(2)获得:i>n/2时,表明适应度值较低的第i个加入者没有获得食物,因饥饿需要前往其他地方觅食以获取能量。
| $ X_{i, j}^{t+1}=\left\{\begin{array}{l} Q \cdot \exp \left(\frac{X_{\text {worst }}^{\prime}-X_{i, j}^{\prime}}{i^2}\right), i>\frac{n}{2} \\ X_{\mathrm{P}}^{t+1}+\left|X_{i, j}^{\prime}-X_{\mathrm{P}}^{t+1}\right| \cdot A^{+} \cdot L, \text { 其他 } \end{array}\right. $ | (2) |
式中:XP为发现者所处的最优位置;Xworst为当前全局最差的位置;A为单位行向量,A+=AT(AAT)-1。
侦查者的位置更新可由公式(3)获得:fi>fbest时,表明麻雀此时处于种群边缘,易受到捕食者攻击;fi=fbest时,表明位于种群中间的麻雀意识到危险,为降低被捕食风险,需向其他麻雀靠近。
| $ X_{i, j}^{t+1}=\left\{\begin{array}{l} X_{\text {beat }}^t+\beta \cdot\left|X_{i, j}^{\prime}-X_{\text {best }}^t\right|, f_i>f_{\text {best }} \\ X_{i, j}^t+K \cdot\left(\frac{\left|X_{i, j}^{\prime}-X_{\text {worst }}^{\prime}\right|}{\left(f_i-f_{\text {worst }}\right)+\varepsilon}\right), f_i=f_{\text {best }} \end{array}\right. $ | (3) |
式中:Xbest为当前全局最优位置;β为步长控制参数;K为[-1, 1]之间的随机数;fi、fbest、fworst分别为当前麻雀个体的适应度值、全局最佳和最差适应度值;ε为非零常数。
SSA-BP算法训练参数设置为:训练次数1 000次;学习率0.01;目标误差0.000 1;初始种群规模40;最大进化代数50;安全值0.6;发现者所占比重0.7(其余为加入者);侦查者所占比重0.2。
3 优化模型预测结果分析 3.1 模型稳定性分析图 14为优化前后训练效果较好的10组计算均方根误差,可以看出,优化后模型相比未优化模型的均方根误差更小,优化前模型最大均方根误差差值为0.1 mm,反映出模型在预测焊道高度和焊道计算高度时会出现较大的波动,预测结果不稳定会对后续进行焊缝质量评估造成重要影响。优化后的模型最大均方根误差差值为0.05 mm,由图 14中数据可计算出,优化前后10组均方根误差的均值分别为0.256、0.122 mm,模型的稳定性得到较好的提高。
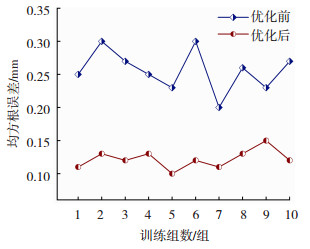
|
图 14 优化前后模型均方根误差 Fig.14 RMSE of model before and after optimization |
训练结束后使用测试样本对模型进行测试,对10组测试样本预测结果进行分析,确认无异常数据。将预测结果与实际测量值进行对比,根据公式(4)和(5)计算得到预测结果的绝对误差和相对误差,如图 15所示。从图 15(a)、(b)中可以看出,优化前焊道高度和焊道计算高度测试结果的最大绝对误差分别为0.14、-0.2 mm,优化后分别为-0.04、0.08 mm,模型的准确率如表 2所示,经过优化后,模型的准确率得到了提升,焊道高度和焊道计算高度预测的相对误差分别保持在±4%、±8%以内。
| $ A^{\prime}=a-A $ | (4) |
| $ \delta=\frac{A^{\prime}}{A} \times 100 \% $ | (5) |
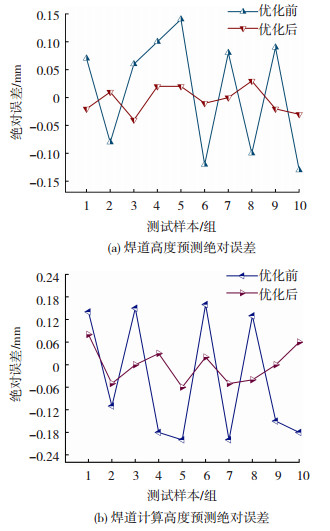
|
图 15 模型预测误差 Fig.15 Model prediction error: (a) absolute error in prediction of weld channel height; (b) absolute error in prediction of calculated height of weld channel |
| 表 2 模型准确率 Table 2 Model accuracy rate |
式中:a为预测值;A为实际测量值;A′为绝对误差;δ为相对误差。
经过麻雀搜索算法优化后,均方根误差减小且平稳,预测结果绝对误差降低,体现出模型的稳定性和预测准确率都有了较大改善,模型的性能有了较好的提升。实验结果对比不仅证明了BP神经网络模型预测焊道几何参数的可行性,也表现出用SSA算法优化BP神经网络模型的可行性。优化后的模型在质量评估时的误差更低,从而能够提高焊接质量和效率。
4 结论为了评估V型坡口焊接时的焊缝成形质量,预测焊道几何参数,本文提出了基于SSA优化的BP神经网络焊道几何参数预测模型。通过实验分析与模型验证,得到的结论如下。
1) 通过实验及分析得出,将焊接工艺参数(焊接电流I、焊接速度v)和熔池宽度(W)作为神经网络模型的输入,焊道高度(h1)和焊道计算高度(h2)作为输出,能够实现BP神经网络对V型坡口多层多道焊道几何参数的预测。
2) 提出了采用麻雀搜索算法优化BP神经网络模型,优化后的模型在稳定性、准确率上都有较大的提升,焊道高度和焊道计算高度的预测相对误差分别保持在±4%、±8%以内,满足V型坡口焊道几何参数预测精度以及后续焊缝成形控制的要求。
| [1] |
唐立. 机械设备加工过程中厚板焊接工艺的应用[J]. 现代制造技术与装备, 2016(2): 101-102. TANG Li. The application of thick plate welding process in the processing of mechanical equipment[J]. Modern Manufacturing Technology and Equipment, 2016(2): 101-102. DOI:10.3969/j.issn.1673-5587.2016.02.047 |
| [2] |
杨立拥, 吴耘森, 葛涛, 等. 机器人焊接中厚板的工艺应用[J]. 机器人技术与应用, 2020(3): 42-44. YANG Liyong, WU Yunsen, GE Tao, et al. Process application of robot welding of medium-thick plates[J]. Robotics and Applications, 2020(3): 42-44. DOI:10.3969/j.issn.1004-6437.2020.03.008 |
| [3] |
武亚鹏, 侯建伟. 国内自动化焊接设备在中厚板领域中的发展及应用[J]. 金属加工(热加工), 2012(22): 15-18, 22. WU Yapeng, HOU Jianwei. The development and application of domestic automated welding equipment in the field of medium thick plate[J]. Metal Processing (Thermal Processing), 2012(22): 15-18, 22. |
| [4] |
李慧平, 王婧, 唐启冬, 等. 水管锅炉焊缝质量检测标准对比研究[J]. 机械, 2018, 45(3): 61-65. YANG Huiping, WANG Jing, TANG Qidong, et al. Comparative study of quality inspection standards for water tube boiler welds[J]. Machinery, 2018, 45(3): 61-65. DOI:10.3969/j.issn.1006-0316.2018.03.016 |
| [5] |
CARO L, ODENBERGER E L, SCHILL M, et al. Prediction of shape distortions during forming and welding of a double-curved strip geometry in alloy 718[J]. International Journal of Advanced Manufacturing Technology, 2020, 107(7-8): 2983-2983. DOI:10.1007/s00170-020-05118-y |
| [6] |
胡雪, 王玉忠, 蒋明鸿, 等. 马鞍形焊缝焊接质量控制研究现状[J]. 热加工工艺, 2021, 50(19): 6-9, 14. HU Xue, WANG Yuzhong, JIANG Minghong, et al. Current status of research on quality control of saddle weld seam welding[J]. Thermal Processing Technology, 2021, 50(19): 6-9, 14. DOI:10.14158/j.cnki.1001-3814.20201393 |
| [7] |
JIAO Ziquan, FENG Ziqiang, CHEN Shenben, et al. An approximate inference scheme based on distance-induced relations: weld forming prediction[J]. IEEE Access, 2021, 9: 62820-6286. DOI:10.1109/ACCESS.2021.3074429 |
| [8] |
JIAO W H, WANG Q Y, CHENG Y C, et al. Prediction of weld penetration using dynamic weld pool arc images[J]. Welding Journal, 2021, 99(11): 295-302. DOI:10.29391/2020.99.027 |
| [9] |
段师剑, 赵勇, 王远传, 等. 建筑钢结构焊缝检测的质量控制探讨[J]. 工程质量, 2018, 36(4): 64-67. DUAN Shijian, ZHAO Yong, WANG Yuanchuan, et al. Discussion on quality control of weld inspection of construction steel structures[J]. Engineering Quality, 2018, 36(4): 64-67. DOI:10.3969/j.issn.1671-3702.2018.04.016 |
| [10] |
ZHU Chenxiao, CHEON Jason, TANG Xinhua, et al. Molten pool behaviors and their influences on welding defects in narrow gap GMAW of 5083 Al-alloy[J]. International Journal of Heat & Mass Transfer, 2018, 126: 1206-1221. DOI:10.1016/j.ijheatmasstransfer.2018.05.132 |
| [11] |
王建军, 陈善本. 铝合金TIG焊自适应控制方法[J]. 上海交通大学学报, 2010, 44(S1): 160-162, 166. WANG Jianjun, CHEN Shanben. Adaptive control method for TIG welding of aluminum alloys[J]. Journal of Shanghai Jiaotong University, 2010, 44(S1): 160-162, 166. |
| [12] |
邢海燕, 葛桦, 等. 基于遗传神经网络的焊缝缺陷等级磁记忆定量化研究[J]. 材料科学与工艺, 2015, 23(2): 33-38. XING Haiyan, GE Hua, et al. Genetic neural network-based quantification of weld defect level magnetic memory[J]. Materials Science and Technology, 2015, 23(2): 33-38. DOI:10.11951/j.issn.1005-0299.20150206 |
| [13] |
王凯, 李冬青, 张忠典, 等. 人工神经网络及其在焊接中的应用与展望[J]. 焊接, 2005(6): 5-9. WANG Kai, LI Dongqing, ZHANG Zhongdian, et al. Artificial neural networks and their applications and perspectives in welding[J]. Welding, 2005(6): 5-9. DOI:10.3969/j.issn.1001-1382.2005.06.002 |
| [14] |
顾新盛, 姚润钢, 孔红雨, 等. 人工神经网络在焊接中的应用研究和发展[J]. 材料开发与应用, 2010, 25(4): 72-76. GU Xinsheng, YAO Rungang, KONG Hongyu, et al. Research and development of artificial neural networks for welding applications[J]. Materials Development and Applications, 2010, 25(4): 72-76. DOI:10.3969/j.issn.1003-1545.2010.04.018 |
| [15] |
WAN Xiaodong, WANG Yuanxun, et al. A comparison of two types of neural network for weld quality prediction in small scale resistance spot welding-science direct[J]. Mechanical Systems and Signal Processing, 2017, 93: 634-644. DOI:10.1016/j.ymssp.2017.01.028 |
| [16] |
LI Shichun, MO Bin, XU Wei, et al. Research on nonlinear prediction model of weld forming quality during hot-wire laser welding[J]. Optics & Laser Technology, 2020, 131: 106436. DOI:10.1016/j.optlastec.2020.106436 |
| [17] |
LI Ran, DONG Manshu, GAO Hongming. Prediction of bead geometry with changing welding speed using artificial neural network[J]. Materials, 2021, 14(6): 14061494. DOI:10.3390/ma14061494 |
| [18] |
高进强, 武传松, 刘新峰. TIG焊背面熔宽的神经网络模糊控制[J]. 焊接学报, 2001, 22(5): 5-8, 4. GAO Jinqiang, WU Chuansong, LIU Xinfeng. Neural network fuzzy control of TIG welding backside melt width[J]. Journal of Welding, 2001, 22(5): 5-8, 4. DOI:10.3321/j.issn:0253-360X.2001.05.002 |
| [19] |
DE R H, HINTON G E, WILLIAMS R J. Learning representations by back propagating errors[J]. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 |
| [20] |
XUE Jiankai, SHEN Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
 2023, Vol. 31
2023, Vol. 31


