近年来，由于环境污染及能源损耗严重，汽车轻量化要求不断提高^[1]。将钢/铝等异种材料结合使用来取代传统的钢材可明显减轻车身质量，但异种材料之间的有效连接却面临挑战^[2]。自冲铆接可代替传统焊接进行同种及异种材料的有效连接，且具备连接速度快，无废料产生等优势^[3]。

目前，国内外学者已对自冲铆接工艺进行了相关研究。Asati等^[4]通过实验对比分析了内锁长度和钉头高度等工艺参数对自冲铆接头强度的影响，发现在保证接头完整性的情况下增大内锁长度可有效提高接头强度。刘洋等^[5]综述了影响自冲铆接头疲劳性能的因素，主要包括铆接工艺、基板参数和添加粘接剂等，提出粘接剂可大幅提高接头的疲劳性能。Atzeni等^[6]通过观察自冲铆接头成形过程中各阶段的轴向截面，探究了接头成形机理，验证了铆接过程中载荷-位移曲线的准确性，并建立可预测接头抗拉伸剪切强度的有限元仿真模型。毛晓东等^[7]选用4种不同长度的铆钉对5182-O铝合金进行铆接，并建立有限元模型对自冲铆接成形工艺进行了预测，研究发现接头强度随铆钉长度的增加呈先上升后下降的趋势。邢保英等^[8]通过对比自冲铆接头与自冲铆-粘接复合接头的强度，发现粘接剂对异种接头的影响大于同种接头。刘洋等^[9]通过正交试验分析了AA5052接头强度受铆接参数的影响，结果表明刺穿压强对接头强度起决定性作用。陈贵坤等^[10]通过响应面法预测铝合金自冲铆接头工艺参数对接头强度的影响，并通过实验验证响应面法可有效预测接头力学性能与铆接参数。综上说明，自冲铆接工艺参数的选取对接头强度具有重要影响，并且随着科技不断发展，研究自冲铆接工艺的方法已不再局限于实验和有限元仿真^[11]。响应面法作为一种操作简易且能够分析各工艺参数对接头强度交互作用的预测方法，已被学者应用到自冲铆接工艺的研究中^[12]。自冲铆-粘接复合连接是自冲铆接工艺中能够显著提高自冲铆接头强度的一种连接方式，因此，建立一种可快速预测自冲铆-粘接复合接头各工艺参数及交互作用对接头强度影响的模型具有重要意义。

本文采用响应面法，建立回归预测模型，以板材硬度、胶层厚度和刺穿压强各因素及其平方项和交互作用为影响因素，探究3种工艺参数对自冲铆-粘接复合接头失效载荷值与能量吸收值的影响，并通过实验验证该回归模型的有效性，以期得到一种能够快速预测自冲铆-粘接复合接头强度的模型。

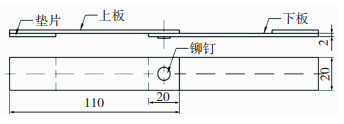
本次实验选用厚度为2 mm的铝合金5182(AA5182)、铝合金5052(AA5052)和铝锂合金1420(AL1420)3种板材，硬度分别为73.4HV、82.1HV和130.1HV，板材尺寸设定为110 mm×20 mm，搭接区域尺寸为20 mm×20 mm。铆钉选用硼钢36MnB4铆钉，硬度为462HRC。粘接剂为3M-DP460环氧树脂胶，并将胶层厚度设置为0.5、1.0及1.5 mm。试件搭接示意图见图 1。

图 Figure1(Fig.Figure1)

图 1 试件搭接示意图(单位：mm) Fig.1 Schematic diagram of test piece lapping

本实验采用德国Bollhoff公司生产的RIVSET VARIO-FC(MTF)型铆接设备对试件进行自冲铆接，如图 2所示，该设备通过电液伺服机构实现连接，其最大许可铆接力为50 kN。铆接过程中使用凸台凹模，冲头直径为7.7 mm。

图 Figure2(Fig.Figure2)

图 2 自冲铆接实验 Fig.2 Self-piercing riveting test

通过试铆确定较优铆接参数，即设置预压压强为5 MPa，整形压强为11 MPa，冲头行程为130.9 mm，刺穿压强分别为17、19和21 MPa，而后对试件进行铆接。将铆接后的试件放入保温箱，24 h后取出并采用MTS Landmark 100材料试验机对试件进行拉伸测试，如图 3所示，试件两端固定尺寸25 mm×20 mm×2 mm垫片以保持拉力对中。拉伸速率设置为5 mm/min，载荷值加载到99%或处于极低数值长时间无明显变化时停止拉伸。

图 Figure3(Fig.Figure3)

图 3 拉伸实验 Fig.3 Tensile test

采用Design-Expert软件对数据进行设计分析，设置板材硬度、胶层厚度和刺穿压强为自变量，失效载荷值与能量吸收值为响应值，进行三因素三水平响应面试验。试验因素及水平如表 1所示，响应面设计与结果如表 2所示。

表1(Table 1)

表 1 试验因素及水平 Table 1 Test factors and levels 因素 水平 -1 0 1 板材硬度(HV) 73.4 82.1 130.1 刺穿压强/MPa 17 19 21 胶层厚度/mm 0.5 1.0 1.5

表 1 试验因素及水平 Table 1 Test factors and levels

表2(Table 2)

表 2 响应面试验设计及结果 Table 2 Response surface test design and results 序号 板材硬度(HV) 胶层厚度/mm 刺穿压强/MPa 失效载荷/N 能量吸收值/J 1 73.4 1.0 21 4 673.6 17.2 2 82.1 1.0 19 4 177.6 14.8 3 130.1 1.0 17 6 718.4 18.6 4 82.1 1.5 17 3 982.0 9.7 5 82.1 1.0 19 4 414.6 12.6 6 73.4 1.0 17 4 696.9 14.7 7 130.1 0.5 19 6 832.2 19.8 8 73.4 1.5 19 4 741.8 16.0 9 82.1 1.5 21 4 189.4 14.6 10 82.1 1.0 19 4 275.9 14.1 11 82.1 0.5 17 4 305.0 16.8 12 73.4 0.5 19 4 410.4 17.2 13 130.1 1.0 21 6 624.3 21.9 14 130.1 1.5 19 5 853.0 19.4 15 82.1 0.5 21 4 184.8 17.5

表 2 响应面试验设计及结果 Table 2 Response surface test design and results

分析表 2数据，以失效载荷值F为响应值，采用最小二乘法对自变量板材硬度x₁、胶层厚度x₂和刺穿压强x₃进行回归拟合。将显著性水平设为0.05，当P值＜0.01时，认为该回归模型极显著；若P值>0.05，则认为回归模型不显著，P值越小则认为显著性越高^[13]。优化后的二次回归模型为

失效载荷值响应面回归模型的方差结果如表 3所示，方差R²=0.993 9>0.9，说明该模型显著性极高，可用于预测接头失效载荷值。对比表中各P值大小，发现板材硬度为单因素中对失效载荷值影响最大的因素，而交互作用中影响最大的为板材硬度与胶层厚度，平方项影响作用与一次项一致。

表3(Table 3)

表 3 失效载荷值方差分析表 Table 3 Failure load value variance analysis table 项目 平方和 自由度 均方误差 F值 P值 方差R2 模型 1.453×107 9 1.614×106 91.01 ＜0.000 1 0.993 9 x1 7.041×106 1 7.041×106 397.00 ＜0.000 1 x2 3.253×105 1 3.253×105 18.34 0.003 7 x3 1 257.17 1 1 257.17 0.071 0.934 0 x1x2 4.091×105 1 4.091×105 23.07 0.002 0 x1x3 4 047.18 1 4 047.18 0.23 0.653 0 x2x3 26 819.27 1 26 819.27 1.51 0.236 0 x12 1.444×106 1 1.444×106 81.41 ＜0.000 1 x22 1.086×105 1 1.086×105 6.12 0.056 0 x32 8 305.00 1 8 305.00 0.47 0.524 0 失拟项 60 330.74 3 20 110.25 1.42 0.438 9

表 3 失效载荷值方差分析表 Table 3 Failure load value variance analysis table

将板材硬度x₁、胶层厚度x₂和刺穿压强x₃三因素作为自变量，能量吸收值E作为响应值，分析各因素及各因素交互作用对响应值的影响。显著性水平仍设为0.05，可建立如下回归模型

由表 4可知，模型P值为0.025＜0.05，失拟项P值为0.348>0.05。方差分析结果表明，模型显著，失拟项不显著，多元相关系数R²为0.923 2，说明该模型拟合度高，可用于预测接头能量吸收值。板材硬度为单因素和平方项中对能量吸收值影响最大的因素，交互作用中刺穿压强和胶层厚度对能量吸收值影响最大。

表4(Table 4)

表 4 能量吸收值方差分析表 Table 4 Analysis of variance of energy absorption value 项目 平方和 自由度 均方误差 F值 P值 方差R2 模型 121.83 9 13.54 6.68 0.025 0.923 2 x1 26.69 1 26.69 13.17 0.015 x2 11.15 1 11.15 5.50 0.066 x3 14.44 1 14.44 7.13 0.044 x1x2 3.13 1 3.13 1.55 0.269 x1x3 0.30 1 0.30 0.15 0.716 x2x3 3.56 1 3.56 1.75 0.243 x12 20.71 1 20.71 10.22 0.024 x22 0.48 1 0.48 0.23 0.649 x32 0.43 1 0.43 0.21 0.663 失拟项 7.62 3 2.54 2.02 0.348

表 4 能量吸收值方差分析表 Table 4 Analysis of variance of energy absorption value

通过试验验证所建立的失效载荷值与能量吸收值回归模型有效性。该验证试验设置为：首先选取4组差异性较大的工艺参数，对其分别进行多次铆接实验，再通过MTS Landmark 100材料试验机进行拉伸测试后取其均值。实验结果如表 5所示，分别将实验所得失效载荷均值以及能量吸收均值的结果与预测值进行对比，发现两组误差均不超过9.4%。说明该回归模型所得结果与实际值误差小，预测结果可信度高。因此，说明利用该回归模型对自冲铆接头静力学性能进行预测的方式可行。

表5(Table 5)

表 5 验证实验结果 Table 5 Verification test resultsx 组号 板材硬度(HV) 胶层厚度/mm 刺穿压强/MPa 失效载荷实验均值/N 失效载荷预测值/N 误差/% 能量吸收实验均值/J 能量吸收预测值/J 误差/% 1 82.1 0.5 19 4 804.4 4 756.8 1.0 15.1 16.0 5.4 2 130.1 1.5 17 6 231.9 5 914.8 5.4 19.1 17.5 9.4 3 82.1 0.6 20 4 200.7 4 441.8 1.6 15.8 14.9 5.9 4 130.1 1.0 18 6 620.9 6 800.5 2.7 18.9 17.8 5.8

表 5 验证实验结果 Table 5 Verification test resultsx

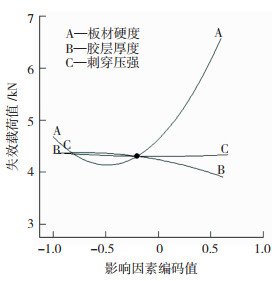
进行单因素分析时，将其中两个单因素数值固定在中值，观察另一因素变化时对其的影响。影响因素编码值最低水平编码为-1，最高水平编码为1，分析结果如图 4所示。分析可得，失效载荷值随板材硬度增加呈先减后增的变化趋势，且变化明显。胶层厚度在0.5~0.9 mm时，曲线较为平稳，随后开始下降。这是由于胶层厚度越大，导致铆钉钉脚扩张难度越大，而钉脚张开度减小是影响失效载荷值降低的重要因素^[14]。因此，失效载荷值随胶层厚度增加而减少，刺穿压强与失效载荷值的变化呈正相关，板材硬度对失效载荷值的影响最大。

图 Figure4(Fig.Figure4)

图 4 单因素对失效载荷值的影响 Fig.4 Influence of single factor on failure load value

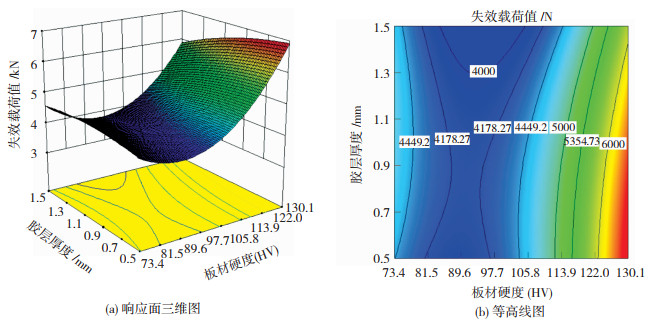
将刺穿压强固定在中值，观察板材硬度与胶层厚度的交互作用对失效载荷值的影响，结果如图 5所示。观察图 5(a)可得，失效载荷值整体呈先减后增的变化趋势，在板材硬度处于82HV~95HV时，失效载荷值位于最低值，且变化幅度较为平缓。随着板材硬度不断增大，失效载荷值大幅上升并在板材硬度处于130.1HV时达到最大值。由此可得，板材硬度处于100HV~130HV且胶层厚度保持在0.5~0.9 mm时，可有效提高失效载荷值。由图 5(b)可得，当板材硬度处于81.5HV~97.7HV之外，等高线主要垂直分布，表明此时胶层厚度的变化对失效载荷值的影响较小。

图 Figure5(Fig.Figure5)

图 5 板材硬度与胶层厚度交互作用对失效载荷值的影响 Fig.5 Effect of interaction between plate hardness and adhesive layer thickness on failure load

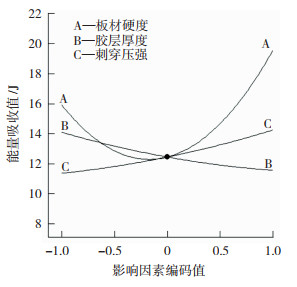
与上述对失效载荷值分析步骤相同，分析三因素对能量吸收值的变化影响，结果如图 6所示, 可以看到，能量吸收值随板材硬度的增大，呈先减后增的弧形变化趋势，弧线中部较为平缓，说明板材硬度处于90HV~110HV时，对能量吸收值的变化影响不大。胶层厚度与能量吸收值呈负相关变化。产生此现象的主要原因有两点，首先胶层厚度增大会阻碍铆钉腿的扩张，其次在树脂胶未干时进行铆接，试件搭接区域的摩擦力大大降低。以上两点共同作用，使能量吸收值减小。能量吸收值随刺穿压强的增加而不断增大，但刺穿压强过大会导致铆扣底部出现裂纹甚至下板被刺穿^[15]。

图 Figure6(Fig.Figure6)

图 6 单因素对能量吸收值的影响 Fig.6 Influence of single factor on energy absorption value

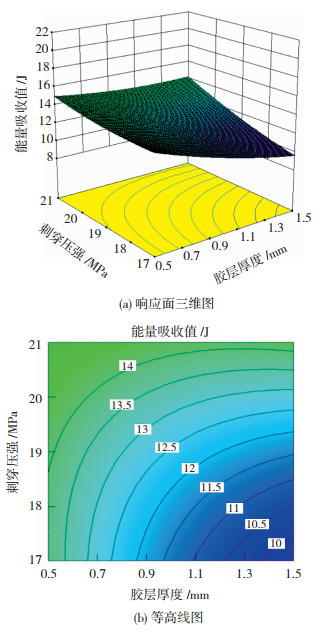
通过方差分析表可得，刺穿压强与胶层厚度的交互作用对能量吸收值影响最大。由图 7可得，能量吸收值平面总体向右倾斜，且在刺穿压强最大，胶层厚度最小时，能量吸收值达到最大值。由图 7(b)可得，等高线呈规律的弧形分布且弧线距离较为均匀。固定胶层厚度，能量吸收值随刺穿压强的增大而增大。反之固定刺穿压强时，能量吸收值随胶层厚度的增加不断减小，与单因素分析结果一致。上述分析表明，胶层厚度过大会减小铆接时搭接区域的摩擦力和拉伸时的失效位移，从而减小能量吸收值。因此铆接时为保证接头具有较大能量吸收值，应将胶层厚度控制在0.5~0.9 mm，并在保证接头残余底厚的情况下，可将刺穿压强增大到20~21 MPa。

图 Figure7(Fig.Figure7)

图 7 胶层厚度与刺穿压强的交互作用对能量吸收值的影响 Fig.7 Effect of the interaction between adhesive layer thickness and piercing pressure on the energy absorption

1) 本文基于响应面法建立了板材硬度、胶层厚度及刺穿压强与失效载荷、能量吸收值之间的多元回归模型，经实验验证，该数学模型预测结果值与实验结果的误差均小于10%，说明此数学模型可用于预测粘铆复合接头静力学性能。

2) 失效载荷响应面预测结果表明，板材硬度对失效载荷的影响最为显著。将板材硬度控制在100HV~130HV，且胶层厚度保持在0.5~0.9 mm时，粘接剂的加入使失效载荷值明显增大。

3) 能量吸收值响应面预测结果表明，各单因素中板材硬度对其影响最大，交互作用中刺穿压强与胶层厚度显著性最高，且刺穿压强与能量吸收值呈正相关变化，实际铆接过程中在确保接头质量的前提下，可将刺穿压强调整到20~21 MPa。