2. 深圳信息职业技术学院 中德机器人学院,广东 深圳 518029;
3. 深圳大学 机电与控制工程学院,广东 深圳 518060
2. School of Sino-German Robotics, Shenzhen Institute of Information Technology, Shenzhen 518029, China;
3. College of Mechanical and Control Engineering Shenzhen University, Shenzhen 518060, China
氧化铝陶瓷凭借其高温下具备的高硬、脆、耐腐蚀等特性,广泛应用于机械、航空航天、汽车、国防工业[1-2],然而,由于氧化铝陶瓷零件大多采用传统烧结工艺和3D打印制备,导致零件表面较粗糙,严重阻碍了氧化铝陶瓷在工业中的应用和性能的提高,因此,降低氧化铝表面粗糙度,提高表面质量是当今学者研究的热点。
激光加工在稳定性、选择性、环保性、非直接接触等方面优于传统的机械加工、化学加工和电解加工方法[3-4]。大量学者的研究表明,激光加工能够降低材料的表面粗糙度[5-8]。在激光加工过程中,由于激光与材料作用时间快且激光强度大,实验中很难观测到加工过程中材料表面形貌的演变,许多学者选择通过数值模拟对金属加工机理、熔池动力学进行研究[9-11]。然而,陶瓷激光加工领域的数值模拟,目前还主要是集中在温度场、应力场分析。Li等[12]研究了陶瓷材料激光熔化建模中热源的影响,研究表明,体积热源比表面热源能够更准确地预测熔池的深度、宽度和截面积。Zhao等[13]利用COMSOL对激光烧蚀氧化铝陶瓷进行了数值模拟,分析了热应力的产生及裂纹扩展路径。华显刚等[14]利用ANSYS模拟激光加工氧化铝陶瓷,并对加工过程中温度场和应力场进行了分析,结果表明,激光辐射区域表面在极短时间达到熔点甚至沸点,热影响区域约为2.5 μm。
综上研究可以发现,目前针对陶瓷材料激光加工的数值模拟尚缺乏对表面形貌演变过程的深入研究,建立适合陶瓷材料激光加工表面形貌演变过程的模型,将有利于更加直观地显示出实验中无法观测的形貌演变过程,为实验加工提供理论指导。本文基于固定激光热源,通过有限元法建立了一个耦合传热和层流的二维轴对称模型,研究了单脉冲激光、多脉冲激光作用于氧化陶瓷表面形貌的演变过程及激光工艺参数对表面粗糙度的影响,并通过实验验证了数值模型的准确性。
1 数值模型的建立 1.1 模型假设在实际激光加工过程中,由于激光是通过一个接一个的激光点作用在材料表面进行加热,因此,可以通过模拟激光点作用在材料表面来描述激光作用于材料表面形貌的演变过程。为了研究激光作用氧化铝陶瓷表面形貌演变过程及激光参数对粗糙度的影响,本文建立了二维瞬态轴对称数值模型,并对模型做出以下假设。
1) 加工过程中熔池内部流动被称为不可压缩的牛顿层流。
2) 材料分布满足各向同性、连续性,且材料属性参数只与温度有关。
3) 忽略等离子体对流体的影响。
4) 忽略加工过程中入射角变化对加工的影响。
5) 忽略加工过程中发生的化学反应。
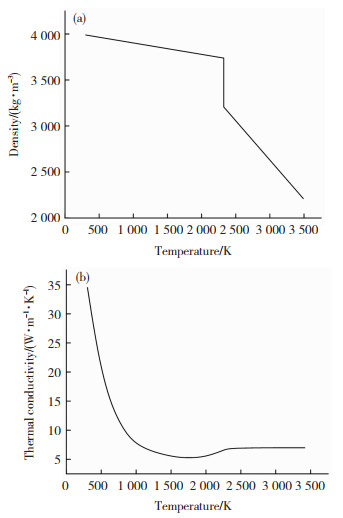
1.2 材料属性模型采用的材料为99% Al2O3,在激光加工过程中,由于材料发生相变,而相变期间吸收或者释放的热量直接影响表面温度、反冲压力、熔池大小和流体速度的大小,因此,模型中应包含温度相关特性,如密度和热导率。图 1为密度和热导率随温度的变化曲线,表 1总结了氧化铝陶瓷的其他材料特性和激光加工参数。
|
图 1 密度(a)和热导率(b)随温度的变化图[15] Fig.1 Variation of density (a) and thermal conductivity (b) with the temperature [15] |
| 表 1 氧化铝陶瓷材料特性及激光加工参数[16-20] Table 1 Alumina ceramic material properties and laser processing parameters[16-20] |
本模型基于COMSOL进行模拟,其中加工过程中传热和层流的控制方程主要由能量、质量和动量守恒组成[21],分别表示为:
| $ \rho C_p^*\left[\frac{\partial T}{\partial t}+\nabla \cdot(\vec{u} T)\right]=\nabla \cdot(k \nabla T) $ | (1) |
| $ \rho \nabla \cdot \vec{u}=0 $ | (2) |
| $ \begin{gathered} \rho\left[\frac{\partial \vec{u}}{\partial t}+\left(\vec{u}-\vec{u}_{\mathrm{m}}\right) \cdot(\nabla \vec{u})\right]= \\ \rho_{\text {ref }} g\left[1-\beta\left(T-T_{\mathrm{m}}\right)\right]+ \\ \nabla \cdot\left\{-p I+\mu\left[\nabla \vec{u}+(\nabla \vec{u})^T\right]\right\} \end{gathered} $ | (3) |
式中:ρ为氧化铝陶瓷的密度;ρref为参考密度;T为加工时表面温度;k为热导率;
| $ C_p^*=C_{p-\mathrm{s}}+L_{\mathrm{m}}\left(\frac{\mathrm{d} f_{\mathrm{L}}}{\mathrm{d} t}\right) $ | (4) |
式中:Cp-s为固态氧化铝比热容;Lm为氧化铝固相转化为液相的熔化潜热;fL为熔池中液相体积分数,其表达式为
| $ f_{\mathrm{L}}=\left\{\begin{array}{cc} 0 & T \leqslant T_{\mathrm{s}} \\ \frac{T-T_{\mathrm{s}}}{T_1-T_{\mathrm{s}}} & T_{\mathrm{s}} \leqslant T \leqslant T_1 \\ I & T \geqslant T_1 \end{array}\right. $ | (5) |
式中:Ts、T1分别为氧化铝的固相、液相线温度。
为了模拟氧化铝陶瓷表面形貌演变过程,采用动网格描述流体内部流动,同时在计算时采用拉普拉斯平滑,从而提高数值模型的收敛性,网格的控制方程[21]为
| $ u_{\text {mesh }} \cdot \vec{n}=u_{\text {mat }} \vec{n} $ | (6) |
式中:umesh为动网格速度;umat为由方程计算的材料速度。
1.4 边界条件为了保证模拟中表面初始轮廓与实际材料表面初始轮廓相符合,采用白光干涉仪测量初始表面轮廓,再通过傅里叶过滤表面高频噪点,避免直接导入模型造成计算不收敛。然后,再将处理后的表面轮廓导入模型,考虑到激光加工过程中材料只在浅表层熔化,建立了二维轴对称模型,其中模型的长宽为200 μm×80 μm,模拟时仅有半个激光辐射在材料表面。模型中各边界条件如图 2所示,其中边界2是对称轴,边界1、4存在表面对环境辐射,边界热源加载在边界1上,边界条件含义及控制方程如表 2所示。

|
图 2 计算域模型示意图 Fig.2 Diagram of computational domain model |
| 表 2 边界条件 Table 2 Boundary conditions |
为了简化模型,激光热源采用平顶热源,热源控制方程为
| $ E_{\text {laser }}=\alpha \frac{P_{\mathrm{pk}}}{\pi r_0^2} \beta_1 $ | (7) |
式中:α为激光吸收率;Ppk为激光峰值功率,可表示为
| $ P_{\mathrm{pk}}=\frac{P}{P_{\mathrm{w}} f} $ | (8) |
β1为用于模拟脉冲激光的方波函数,可表示为
| $ \beta_1=\operatorname{rect1}\left[\bmod \left(t, \frac{1}{f}\right)\right] $ | (9) |
考虑到模型中材料蒸发主要产生反冲压力和材料去除两个影响,其中反冲压力Pr表示为
| $ P_{\mathrm{r}}=\frac{1+\beta_{\mathrm{r}}}{2} P_{\mathrm{sat}}\left(T_{\mathrm{f}}\right) $ | (10) |
式中:Tf为发生蒸发时表面温度;βr为逆向扩散系数;Psat为饱和蒸汽压,可表示为[9]
| $ P_{\text {sat }}=P_{\text {atm }} \exp \left[\frac{\Delta H_{\mathrm{v}}}{k_{\mathrm{B}} T_{\mathrm{v}}}\left(1-\frac{T_{\mathrm{v}}}{T_{\mathrm{f}}}\right)\right] $ | (11) |
式中:Patm为标准大气压;ΔHv为单个原子汽化的相变焓;kB为波尔兹曼常数。
模型中材料去除通过汽化热通量损失Qevap表示为
| $ Q_{\text {evap }}=\left(1-\beta_{\mathrm{r}}\right)\left(\frac{m}{2 \pi k_{\mathrm{B}} T_{\mathrm{f}}}\right)^{1 / 2} P_{\mathrm{sat}}\left(T_{\mathrm{f}}\right) \times L_{\mathrm{v}} $ | (12) |
式中:m为单个原子的质量;Lv为蒸发潜热。
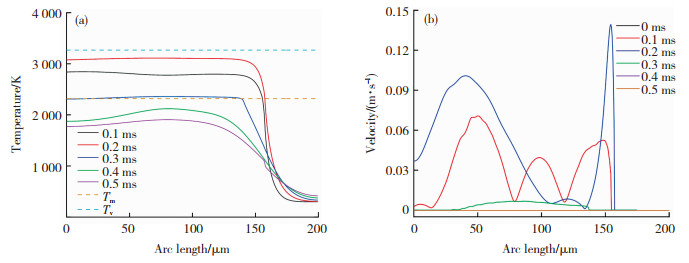
2 模拟结果分析 2.1 单脉冲激光作用下材料表面形貌演变过程为了模拟单个脉冲激光作用于氧化铝陶瓷表面形貌演变过程,光斑中心作用在r=0 μm处,其中脉冲宽度0.2 ms,功率为52 W,激光聚焦后的光斑直径为0.314 mm,氧化铝陶瓷材料的相关参数如表 1所示。为了模拟出脉冲激光加热的效果,在激光热源处加载方波函数,该方波函数持续加热时间为0.2 ms,冷却时间0.3 ms。图 3(a)给出了激光功率52 W不同时刻材料表面的温度变化,可以看出:0~0.2 ms表面温度逐渐上升,最大表面温度达3 110 K, 随后进入冷却阶段;0.5 ms时表面最大温度降低至1 905 K。图 3(b)为0~0.5 ms材料表面流体速度的变化图,由于本模型设置固体动力粘度为105 Pa ·s,液体动力粘度为0.03 Pa ·s,因此,当温度低于熔化温度,辐射区域流体速度被限制为0,随着辐射时间的增加,流体突破动力粘度的限制,其最大速度达0.14 m/s,在冷却阶段,随着温度的降低,辐射区域流体速度逐渐下降,直到材料重新凝固,流体速度被限制为0 m/s。
|
图 3 0~0.5 ms材料表面温度及熔池内流体速度大小分布:(a)表面温度分布图;(b)熔池内流体速度大小分布图 Fig.3 0~0.5 ms material surface temperature and fluid velocity distribution in molten pool: (a) surface temperature distribution; (b) fluid velocity distribution in molten pool |
使用表面轮廓曲率来衡量加工后材料表面的平滑程度,理论上来说,曲率越趋于零,平滑效果越好。图 4(a)是0~0.5 ms材料表面轮廓曲率变化图,可以看出,辐射区域在加热阶段0~0.2 ms,由于熔池中流体在毛细力和热毛细力等驱动力作用下,流体由表面凸起向凹陷区域流动,材料表面在一定程度上得到平滑,因此,0~0.2 ms表面轮廓曲率逐渐降低。辐射区域在冷却阶段0.2~0.5 ms,表面温度逐渐降低,在0.3 ms时,由图 3(a)可知,表面温度下降到熔化温度附近,熔池尺寸逐渐缩小,材料表面轮廓曲率进一步减小。此外,可发现各个时刻熔池边缘材料表面轮廓曲率突变,这是因为熔池边缘材料的冷却速率高于熔池其他区域,边缘处流体材料冷却后迅速凝固,熔池边缘流体得不到充分的平滑。图 4(b)给出了0~0.5 ms时材料表面轮廓高度变化图。对比加工前0 ms和加工后0.5 ms时辐射区域材料表面轮廓高度变化,可以发现加工后材料表面轮廓高度差由8 μm下降到3.5 μm,同时,可以发现轮廓波峰高度降低而波谷高度增加,因此,单脉冲激光对材料表面具有显著的平滑效果。

|
图 4 0~0.5 ms材料表面轮廓曲率及表面轮廓高度变化:(a)表面轮廓曲率变化图;(b)表面轮廓高度变化图 Fig.4 0~0.5 ms material surface contour curvature and surface contour height change: (a) curvature change diagram of surface contour; (b) surface contour height variation diagram |
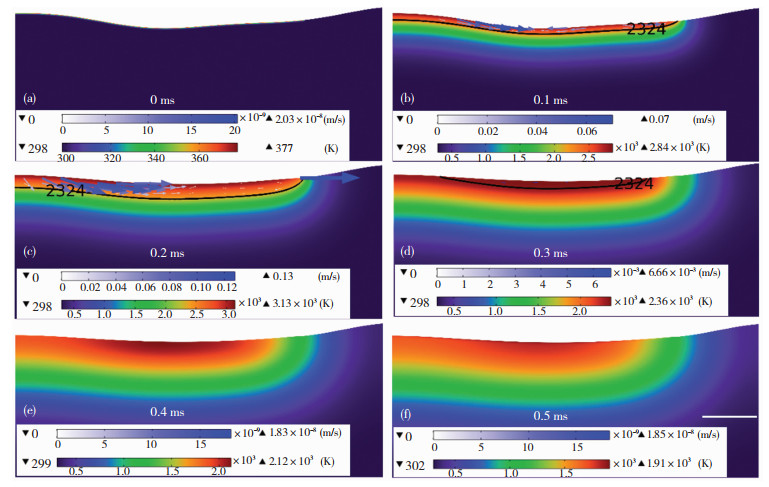
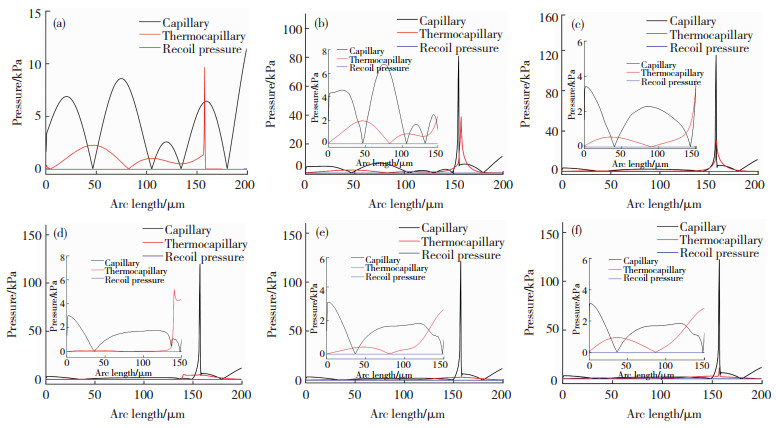
图 5给出了0~0.5 ms材料表面熔池演变过程,图中箭头方向表示流体流动方向,箭头的大小与流速呈正比,其中黑色曲线表示材料熔化温度等温线,等温线以内表示材料为液态,反之为固态。图 6为0~0.5 ms材料表面毛细力、热毛细力、反冲压力分布,可以看到在0.1 ms,辐射区域材料形成一个深度仅为3.5 μm的熔池(图 5(b)),熔池内流体由表面凸起向凹陷区域流动,结合图 6(b)可知,熔池中流体的驱动力主要为毛细力。随着辐射时间的增加,在0.2 ms时,熔池深度进一步加深至8 μm(图 5(c)),熔池内流体流动更加剧烈, 值得注意的是,在熔池的边缘区域(140<r<152 μm)流体向表面轮廓高的位置流动,结合图 6(c), 这是因为该边缘区域热毛细力大于毛细力,流体由热毛细力驱动从温度中心向边缘位置流动。随后辐射区域进入冷却阶段,在0.3 ms时,由于表面对环境辐射和热对流,导致熔池尺寸急剧缩小(图 5(d)),随着温度的降低,在0.4~0.5 ms时,熔池内流体逐渐凝固,此时毛细力、热毛细力将无法驱动流体流动。
|
图 5 0~0.5 ms材料表面形貌演变过程 Fig.5 0~0.5 ms material surface morphology evolution process: (a) 0 ms; (b) 0.1 ms; (c) 0.2 ms; (d) 0.3 ms; (e) 0.4 ms; (f) 0.5 ms |
|
图 6 0~0.5 ms材料表面毛细力、热毛细力、反冲压力分布 Fig.6 0~0.5ms material surface capillary force, thermal capillary force and recoil pressure distribution: (a) 0 ms; (b) 0.1 ms; (c) 0.2 ms; (d) 0.3 ms; (e) 0.4 ms; (f) 0.5 ms |
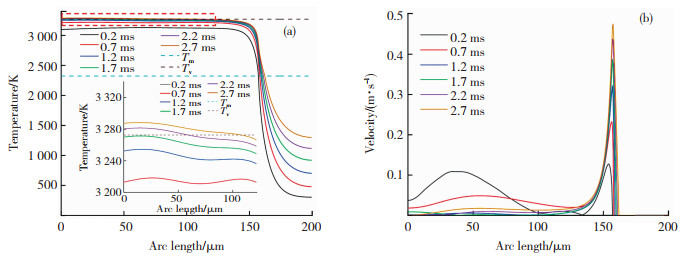
通过单脉冲激光作用材料表面形貌演变可以发现,在单脉冲加工后材料表面形貌得到一定的平滑,但是辐射后材料表面凸起并未完全消失。在实际加工实验中,材料表面接受单个或者多个脉冲辐射,材料表面才能得到完全平滑,因此,在单脉冲加工的基础上,本文增加一定数量的脉冲次数来研究材料表面形貌演变过程。图 7(a)为脉冲1~6次峰值温度曲线,可以看出,随着脉冲次数的增加,辐射区域峰值温度逐渐增加,0.2~1.7 ms时,表面最大温度达3 271 K, 材料表面最大温度一直处于熔化温度和蒸发温度之间,而2.2~2.7 ms时,材料表面最大温度突破蒸发温度,表面最大温度达3 288 K, 由于蒸发产生的反冲压力也将驱动流体流动,此时熔池中的流体将会受到毛细力、热毛细力、反冲压力3个驱动力共同作用。图 7(b)为0.2~2.7 ms熔池中流体速度分布曲线。观察发现,0.2~1.7 ms时,在熔池中心部位(0<r<80 μm),流体流速随着脉冲数量的增加而降低,这是因为在前一个脉冲作用下,熔池中心部位凸起逐渐被平滑,驱动熔池流动的毛细力降低,熔池中流体流动速度减缓。在2.2~2.7 ms时,熔池部分材料被蒸发,熔池中流体流速受反冲压力的影响轻微增加。值得注意的是,在熔池的边缘位置,随着脉冲数量的增加,熔池逐渐向外扩展,边缘处流体流速逐渐增加。
|
图 7 0.2~2.7 ms材料表面温度及熔池内流体速度大小分布:(a)表面温度分布图;(b)熔池内流体速度大小分布图 Fig.7 0.2~2.7 ms material surface temperature and molten pool fluid velocity distribution: (a) surface temperature distribution; (b) distribution of fluid velocity in molten pool |
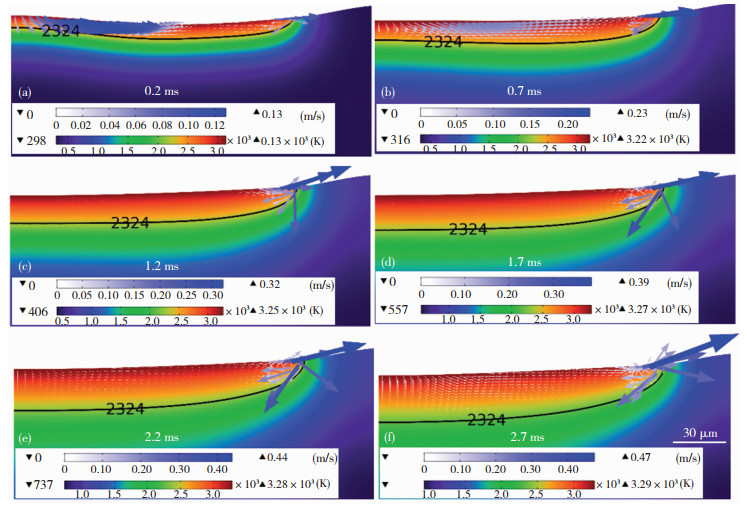
图 8给出了0.2~2.7 ms材料表面熔池演变过程,图 9为对应时刻材料表面毛细力、热毛细力、反冲压力分布。熔池中心部位(0<r<80 μm),在0.2~1.7 ms时,由于材料表面凸起较为明显,熔池中心区域大部分由毛细力占主导地位(图 9(a)~(d)),故熔池中流体在以毛细力为主导的驱动力下由轮廓高的区域向低的区域流动。随着辐射时间的增加,材料表面接受脉冲的次数增加,在2.7 ms时,熔池中反冲压力剧增,超过毛细力和热毛细力成为熔池中的主要驱动力,如图 9(f)所示,熔池中的反冲压力驱动流体向下并在浮力的作用下向熔池的边缘流动。值得注意的是,图 8中各时刻熔池边缘位置出现了明显的回流,结合图 9可知,在熔池边缘位置,熔池中流体由热毛细力驱动,而氧化铝陶瓷材料的表面温度张力系数为负,因此,该区域流体由温度中心向边缘流动,并在固液边界位置形成回流。
|
图 8 0.2~2.7 ms材料表面形貌演变过程 Fig.8 0.2~2.7 ms material surface morphology evolution process: (a) 0.2 ms; (b) 0.7 ms; (c) 1.2 ms; (d) 1.7 ms; (e) 2.2 ms; (f) 2.7 ms |

|
图 9 0.2~2.7 ms材料表面毛细力、热毛细力、反冲压力分布 Fig.9 0.2~2.7 ms surface capillary force, thermal capillary force and recoil pressure distribution: (a) 0.2 ms; (b) 0.7 ms; (c) 1.2 ms; (d) 1.7 ms; (e) 2.2 ms; (f) 2.7 ms |
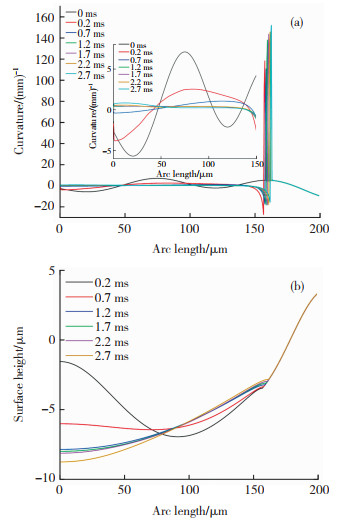
图 10为0.2~2.7 ms时刻材料上表面轮廓曲率及轮廓高度变化图。对比加工前后表面轮廓曲率,总体来说,脉冲激光加工后熔池中心部位材料表面轮廓曲率均大幅降低,脉冲2~3次(0.7~1.2 ms)具有最佳平滑效果,而熔池边缘位置则是由于高冷却速率形成新的轮廓曲率突变。对比材料上表面轮廓高度变化可以发现(图 10(b)),在0<r<70 μm位置,表面凸起基本被消除,由于温度的升高和负的表面张力系数,导致熔池中出现了明显的向外流动模式,属于典型的热毛细力诱导流动,因此,出现了该区域加工后向下微凹陷,在2.7 ms时,表面凹陷深度有微小的加剧,则主要是2.7 ms熔池温度超过了材料蒸发温度,由此产生的竖直向下的反冲压力作用于该区域熔池上表面,从而加剧了凹陷程度,表面逐渐变粗糙。
|
图 10 0.2~2.7 ms材料表面轮廓曲率和轮廓高度变化图:(a)表面轮廓曲率变化图;(b)表面轮廓高度变化图 Fig.10 0.2~2.7 ms material surface contour curvature and surface contour height change: (a) curvature change diagram of surface contour; (b) surface contour height variation diagram |
在脉冲激光加工过程中,影响加工效果的因素很多,其中激光功率、频率、脉宽是加工过程中重要的工艺参数。采用控制变量法研究激光工艺参数对表面粗糙度的影响,图 11(a)、(b)、(c)分别是不同频率、脉宽、功率所得加工表面粗糙度及最大熔池深度变化图,其中0.2、10 ms分别表示熔融态和冷却凝固后表面粗糙度。

|
图 11 不同工艺参数单脉冲激光加工后表面粗糙度及熔池最大深度变化图:(a)不同频率; (b)不同脉宽; (c)不同功率 Fig.11 Variation of surface roughness and maximum depth of melt pool after single-pulse laser processing with different process parameters: (a) different frequencies; (b) different pulse width; (c) different power |
从图 11(a)可以看出,随着脉冲频率的增加,粗糙度则随之增加,这主要是由于在其他工艺参数不变的情况下,增加脉冲频率会导致单脉冲激光通量减小,熔池最大熔化深度逐渐降低,熔池内材料熔化不充分,材料表面粗糙度逐渐增加;图 11(b)中随着激光脉宽的增加,表面粗糙度呈现先减小而后增大的趋势,这主要是由于激光脉宽增加,辐射时间延长,材料表面在脉宽0.1~0.25 ms时表面粗糙度降低,超过0.25 ms后激光通量继续下降,导致熔池最大深度急剧下降,辐射区域材料熔化不充分,材料表面粗糙度逐渐上升;图 11(c)中,在其他工艺参数不变时,随着激光功率的增加,材料表面粗糙度呈现先减小后增加的趋势,同时熔池最大深度处于一直上升趋势,在功率42~72 W时,激光功率增大导致激光通量增大,材料得到充分熔化,表面粗糙度降低,82~92 W时,由于激光功率增大,材料表面温度急剧增大,超过材料蒸发温度,辐射区域部分材料以气体形式逸出,同时逸出的气体产生的反冲压力向下作用在流体材料表面,因此,材料表面粗糙度逐渐增加。
3 实验验证由于模型中对加工过程进行了假设简化,因此需要通过加工实验对模拟结果进行验证,为了保证脉冲激光加工实验的进行,采用CO2激光器搭建了加工实验装置,其能量分布是一个平顶式的激光束,如图 12所示,实验装置主要包括激光器(FSTI100SWC, SYNRAD, USA)、三维动态聚焦振镜(RF8330-3D-1200,金海创,江苏,中国)、三维调节架等,其中激光器的功率输出范围为0~ 150 W,振镜工作焦距为550 mm,幅面为400 mm× 400 mm。由于激光加工涉及复杂的物理过程,难以对其演变过程进行实时检测,因此,本文通过激光共聚焦显微镜获取实验加工点的表面粗糙度Rt及熔池直径与模拟结果对比来验证模拟的准确性。

|
图 12 实验装置 Fig.12 Experimental apparatus |
加工实验和模拟均采用激光功率为52 W、脉宽0.2 ms、频率为2 kHz。图 13为脉冲激光辐射1.7 ms时加工点的SEM图像。从图 13(a)可以发现,激光辐射后材料表面形成了明显的圆形熔池,材料表面得到一定的平滑,值得注意的是,表面产生了明显的微裂纹,这主要是由于激光加工产生大的热应力引起的,对比图 13(b)、(c)可以观察到,加工后材料表面粉末颗粒进一步细化,颗粒之间的空隙缩小,这主要是由于激光作用后材料表面形成了致密的熔融层导致的。

|
图 13 激光辐射1.7 ms时材料表面加工点实际SEM图像 Fig.13 Actual SEM image of material surface processing point at 1.7 ms laser irradiation |
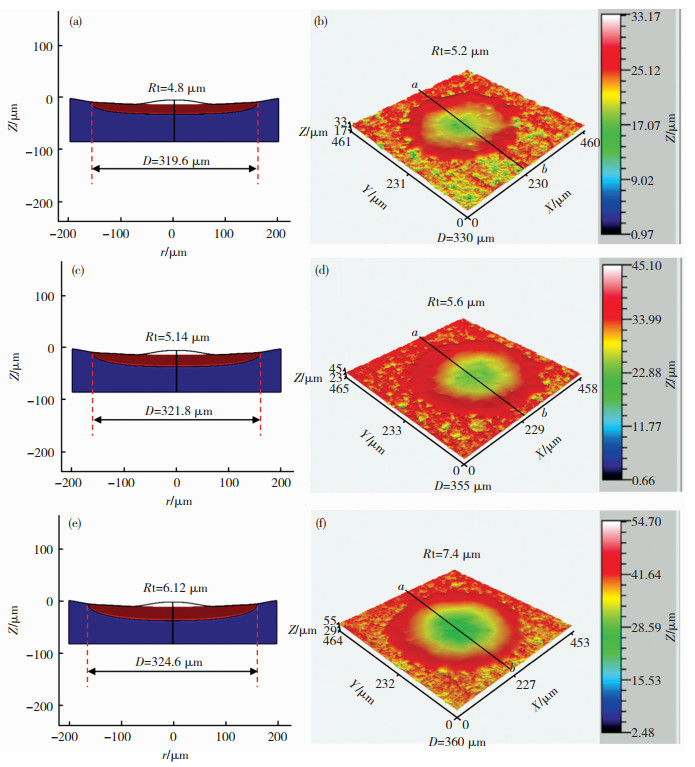
为了检验模拟的准确性,分别选取辐射时间为1.7、2.2、2.7 ms熔池的表面粗糙度Rt及熔池直径D进行对比。图 14为实验和模拟加工所得熔池表面粗糙度Rt和熔池宽度对比图,图 14(a)、(c)、(e)为模拟熔池截面形貌图,其中黑色曲线表示原始轮廓曲线,图 14(b)、(d)、(f)为实验所得熔池形貌图。此外,表 3给出了实验和模拟所得数据值的比较。结合图 14和表 3可知,模拟结果所得Rt和熔池直径D均小于实验测量值,最大误差控制在21%以内,考虑到模型进行了一定的假设简化,因此,本文认为实验与模拟结果相吻合,采用该模型进行数值模拟具有较高的准确性。
|
图 14 实验和模拟加工所得熔池表面粗糙度Rt和熔池宽度D对比图 Fig.14 Comparison of melt pool surface roughness Rt and melt pool width D obtained by experiment and simulation processing |
| 表 3 实验和模拟所得数据值比较 Table 3 Comparison of experimental and simulated data |
本文建立了一个耦合传热和层流的二维轴对称模型,研究了单脉冲、多脉冲激光作用氧化陶瓷表面形貌的演变过程,及不同激光工艺参数对表面粗糙度的影响,并通过实验对数值模型进行了验证。
1) 采用激光功率为52 W、脉宽0.2 ms、频率为2 kHz的单脉冲激光作用于氧化铝陶瓷表面时,加工后材料表面轮廓曲率降低,具有显著的平滑效果,熔池内部流体主要是在毛细力的驱动下由波峰流向波谷,而边缘位置则主要在热毛细力的作用下由温度中心向固液边界流动。
2) 采用相同参数下的多脉冲激光作用氧化铝陶瓷表面时,在脉冲2~3次时,具有最佳平滑效果,随着脉冲次数的增加,熔池内部流体主要驱动力由毛细力逐渐转变为反冲压力,同时反冲压力的出现,增加了熔池表面轮廓的凹陷程度,反冲压力是造成材料表面平滑效果减弱的主要原因。
3) 采用不同激光工艺参数的脉冲激光作用于氧化铝陶瓷表面时,保持其他参数不变,较大的频率或者脉冲宽度都会导致激光通量降低,材料表面得不到充分的熔化,粗糙度降低不明显,然而较大的激光功率则会导致激光通量过大,从而使表面粗糙度增加。
| [1] |
ZHANG Chao, LIANG Yingdong, CUI Zhijie, et al. Study on the effect of ultrasonic vibration-assisted polishing on the surface properties of alumina ceramic[J]. Ceramics International, 2022, 48(15): 21430-21447. DOI:10.1016/j.ceramint.2022.04.105 |
| [2] |
ZHANG Ximin, JI Lingfei, ZHANG Litian, et al. Polishing of alumina ceramic to submicrometer surface roughness by picosecond laser[J]. Surface and Coatings Technology, 2020, 397: 125962. DOI:10.1016/j.surfcoat.2020.125962 |
| [3] |
BHADURI D, GHARA T, PENCHEV P, et al. Pulsed laser polishing of selective laser melted aluminium alloy parts[J]. Applied Surface Science, 2021, 558: 149887. DOI:10.1016/j.apsusc.2021.149887 |
| [4] |
LIU E, CHEN Xi, PAN Zhimin, et al. Enhanced corrosion performance of S136 steel after nanosecond pulsed laser polishing[J]. Journal of Materials Research and Technology, 2022, 20: 1328-1340. DOI:10.1016/j.jmrt.2022.07.132 |
| [5] |
LIU Bowen, MI Gaoyang, WANG Chunming. Study on the morphology and microstructure of 5A06 alloy by high-pulse-frequency pulsed laser micro polishing[J]. Materials Chemistry and Physics, 2020, 255: 123500. DOI:10.1016/j.matchemphys.2020.123500 |
| [6] |
VADALI M, MA C, DUFFIE N A, et al. Pulsed laser micro polishing: Surface prediction model[J]. Journal of Manufacturing Processes, 2012, 14(3): 307-315. DOI:10.1016/j.jmapro.2012.03.001 |
| [7] |
王涛, 康清川. 脉冲光纤激光抛光Ti6Al4V的实验分析及研究[J]. 激光与红外, 2022, 52(3): 336-342. WANG Tao, KANG Qingchuan. Experimental analysis and research of pulsed fiber laser polishing Ti6Al4V[J]. Laser & Infrared, 2022, 52(3): 336-342. DOI:10.3969/j.issn.1001-5078.022.03.005 |
| [8] |
徐一帆, 邵景珍, 林颖, 等. 硬脆材料的激光表面抛光研究进展[J]. 激光与光电子学进展, 2022, 59(13): 32-39. XU Yifan, SHAO Jingzhen, LIN Ying, et al. Research progress in laser surface polishing of hard and brittle materials[J]. Laser & Optoelectronics Progress, 2022, 59(13): 32-39. DOI:10.3788/LOP202259.1300003 |
| [9] |
LI Kai, ZHOU Houming, ZHAO Zhenyu, et al. A study on transient molten pool dynamics in laser polishing of Ti6Al4V using numerical simulation[J]. Journal of Manufacturing Processes, 2021, 65: 478-490. DOI:10.1016/j.jmapro.2021.03.045 |
| [10] |
XU Jilin, ZOU Ping, WANG Wenjie, et al. Study on the mechanism of surface topography evolution in melting and transition regimes of laser polishing[J]. Optics & Laser Technology, 2021, 139: 106947. DOI:10.1016/j.optlastec.2021.106947 |
| [11] |
ZHOU Hao, ZHOU Houming, ZHAO Zhenyu, et al. Numerical simulation and verification of laser-polishing free surface of S136D die steel[J]. Metals, 2021, 11(3): 400. DOI:10.3390/met11030400 |
| [12] |
LI JF, LI L, STOTT F H. Comparison of volumetric and surface heating sources in the modeling of laser melting of ceramic materials[J]. International Journal of Heat and Mass Transfer, 2004, 47(6-7): 1159-1174. DOI:10.1016/j.ijheatmasstransfer.2003.10.002 |
| [13] |
ZHAO Wanqin, MEI Xuesong, YANG Zixuan. Simulation and experimental study on group hole laser ablation on Al2O3 ceramics[J]. Ceramics International, 2022, 48(4): 4474-4483. DOI:10.1016/j.ceramint.2021.10.233 |
| [14] |
华显刚, 魏昕, 周敏, 等. 355nm紫外激光加工Al2O3陶瓷的温度场和应力场仿真分析[J]. 机械设计与制造, 2014(12): 159-162. HUA Xiangang, WEI Xin, ZHOU Min, et al. Simulation analysis of 355 nm UV laser polishing alumina ceramic temperature field and stress field[J]. Machinery Design & Manufacture, 2014(12): 159-162. DOI:10.19356/j.cnki.1001-3997.2014.12.042 |
| [15] |
VORA H D, SANTHANAKRISHNAN S, HARIMKAR S P, et al. One-dimensional multipulse laser machining of structural alumina: Evolution of surface topography[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(1): 69-83. DOI:10.1007/s00170-012-4709-8 |
| [16] |
MCQUARRIE M. Thermal conductivity: VⅡ, analysis of variation of conductivity with temperature for Al2O3, BeO, and MgO[J]. Journal of the American Ceramic Society, 1954, 37(2): 91-95. DOI:10.1111/j.1551-2916.1954.tb20106.x |
| [17] |
PARADIS P F, ISHIKAWA T. Surface tension and viscosity measurements of liquid and undercooled alumina by containerless techniques[J]. Japanese Journal of Applied Physics, 2005, 44(7R): 5082. DOI:10.1143/jjap.44.5082 |
| [18] |
QUINTERO F, VARAS F, POU J, et al. Theoretical analysis of material removal mechanisms in pulsed laser fusion cutting of ceramics[J]. Journal of Physics D: Applied Physics, 2005, 38(4): 655. DOI:10.1088/0022-3727/38/4/021 |
| [19] |
SAMANT A N, DAHOTRE N B. Laser machining of structural ceramics——A review[J]. Journal of the European Ceramic Society, 2009, 29(6): 969-993. DOI:10.1016/j.jeurceramsoc.2008.11.010 |
| [20] |
鄢锉, 李力钧, 李大生. Al2O3陶瓷对CO2激光吸收率试验测定[J]. 湖南大學學報(自然科學版), 2008, 35(1): 41-44. YAN Cuo, LI Lijun, LI Dasheng. Experimental measurement on the absorption coefficients of Al2O3 ceramics to CO2 laser radiation[J]. J Hunan Univ (Nat Sci), 2008, 35: 41-44. |
| [21] |
LI Kai, ZHAO Zhenyu, ZHOU Houming, et al. Numerical analyses of molten pool evolution in laser polishing Ti6Al4V[J]. Journal of Manufacturing Processes, 2020, 58: 574-584. DOI:10.1016/j.jmapro.2020.08.045 |
 2023, Vol. 31
2023, Vol. 31


