1. 河钢材料技术研究院, 石家庄 050000
1. HBIS Material Technology Research Institute, Shijiazhuang 050000, China
随着环境和能源问题的日趋加重,轻量化成为汽车制造行业的一个大趋势[1],汽车厂为实现轻量化而尽可能使用更薄的高强钢,由此带来的对抗凹性能的影响受到更多的关注[2-3]。作为评价和反映车身覆盖件表面质量和使用性能的抗凹性能,直接反映了车身覆盖件在外部载荷作用下抵抗凹陷变形的能力[4]。抗凹性能受材料厚度、屈服强度、成形引起的厚度减薄和应变硬化等多种因素的影响[5-7]。为更好评价材料的抗凹性能,国家标准GB/T 34477—2017以及中国汽车工程学会技术规范SAE-China J3201—2013分别制定了金属材料和汽车覆盖件板材的抗凹性能试验方法[8-9],同时,随着抗凹有限元数值模拟技术的不断完善,国内外学者开展了相关仿真计算和研究[6, 10-12]。但是目前抗凹性能仿真未全面考虑材料厚度、屈服强度、成形因素、材料硬化模型等对抗凹性能的影响,不能够真实反映试样的抗凹性能。本文按照SAE-China J3201—2013标准进行试样成形和抗凹性能测试,并开展成形、抗凹性能仿真计算,考虑成形引起的厚度减薄和应变硬化对抗凹性能的影响,实现了成形-抗凹性能联合仿真计算,对比了不同计算方法对抗凹性能结果的影响。
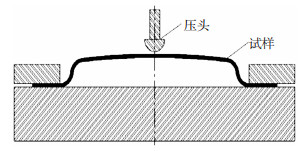
1 抗凹性能测试 1.1 抗凹实验方法研究对象为汽车外板常用牌号HC180BD+Z(厚度0.65 mm)。首先利用模具,并通过控制成形行程将板料冲压成两种变形量的试样,然后使用半球形钢制压头以一定加载速度对试样进行加载,记录力-位移曲线,最后通过曲线计算获得初始刚度和失效凹陷载荷。图 1为实验示意图[9],其中压头直径为25.4 mm,图 2为抗凹性能测试试样的形状和尺寸。
|
图 1 抗凹实验示意图 Fig.1 Schematic diagram of dent resistance test |

|
图 2 抗凹试样尺寸(单位:mm) Fig.2 Sample size of dent resistance |
冲压成形过程:首先将材料裁剪成305 mm×127 mm的平板试样并放置在压边圈上方;然后凹模向下与压边圈接触后继续向下运动,为保证板材被完全锁定,凹模设置刺状筋;最后凹模向下使板料与凸模接触,通过控制凹模行程获得不同成形深度的试样。本文分别控制凹模行程获得成形深度H为16和24 mm的两种试样。
抗凹实验过程:在装备抗凹实验工装的拉伸试验机上进行抗凹性能实验,首先将试样固定在实验台,保证实验过程中对试样紧固,将直径为25.4 mm的钢制压头垂直放在试样测试位置表面并保持同轴;然后使用钢制压头以10 mm/min的速度对试样进行加载,加载过程中采用载荷与位移传感器记录足够的实验数据,获得力-位移曲线;最后对10~25 N范围内的力-位移数据进行线性拟合获得初始刚度,力-位移曲线斜率第一次为0时对应的力为失稳凹陷载荷。
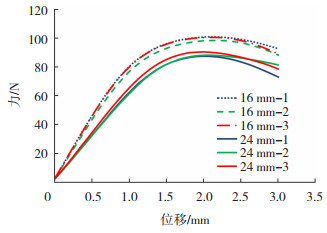
1.3 实验结果由实验获得的力-位移曲线(图 3)可以看出,成形深度16 mm试样的初始刚度和失稳载荷整体高于成形深度24 mm试样。表 1为初始刚度和失稳载荷结果,实验结果一致性较好,成形深度16 mm试样的初始刚度和失稳凹陷载荷的平均值分别为86.6 N/mm和100.0 N;成形深度24 mm试样的初始刚度和失稳凹陷载荷平均值分别为62.3 N/mm和88.8 N。成形深度24 mm试样的初始刚度低于成形深度16 mm试样,主要是因为:1)成形深度24 mm试样H值大(图 2),侧壁更长,引起初始刚度下降;2)成形深度24 mm试样变形量大,厚度减薄率大,试样实际厚度小,引起初始刚度下降。
|
图 3 力-位移实验曲线 Fig.3 Force-displacement experimental curve |
| 表 1 初始刚度和失稳凹陷载荷实验结果 Table 1 Test result of the initial stiffness and buckling effect load |
成形引起试样厚度减薄和应变硬化,会影响试样的抗凹性能[6-7, 11],因此在抗凹性能计算时应该考虑这种影响。为了对比厚度减薄和应变硬化对抗凹性能仿真结果的影响,本文分别进行了计算,并与实验结果进行了对比。本节进行了不考虑厚度减薄和应变硬化影响的抗凹性能仿真。
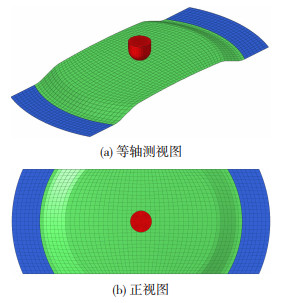
2.1 抗凹性能仿真模型利用Catia软件按图 2试样尺寸建立3D模型,其中H分别设定为16和24 mm。利用hypermesh前处理软件导入试样3D模型,抽取中面并划分网格,赋材料属性和厚度属性,最后建立约束和加载条件,完成抗凹有限元模型(图 4)。试样采用Belytschko-Tsay全积分壳单元方程,网格尺寸5 mm。材料采用MAT_PIECEWISE_LINEAR_PLASTICITY模型,材料性能参数见表 2。压头采用MAT_RIGID刚性材料模型,实体单元。试样两侧法兰约束6个自由度,压头加载速度1 mm/s。利用Ls-dyna软件进行抗凹性能计算,输出压头与试样之间的接触力-时间曲线,并转化为力-位移曲线。
|
图 4 抗凹实验模型 Fig.4 Dent resistance model: (a) isometic view; (b) front view |
| 表 2 HC180BD+Z材料性能 Table 2 Material properties of HC180BD+Z |
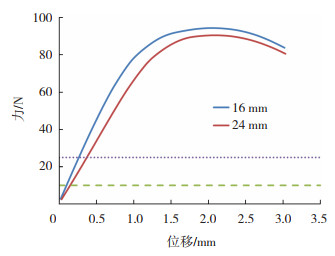
图 5为仿真计算的力-位移曲线,可以看出成形深度16 mm试样的曲线整体高于成形深度24 mm试样,这与实验结果相符。
|
图 5 力-位移仿真曲线 Fig.5 Force-displacement simulation curve |
力-位移曲线计算的初始刚度和失效凹陷载荷(表 3)与实验结果对比,初始刚度仿真结果整体高于实验值,其中成形深度24 mm试样的初始刚度仿真结果偏大7.8%;成形深度16和24mm试样失稳凹陷载荷仿真结果与实验值分别偏差5.7%和2.0%。
| 表 3 初始刚度和失效凹陷载荷仿真结果 Table 3 Simulation result of the initial stiffness and buckling effect load |
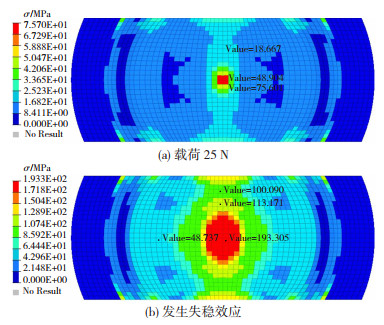
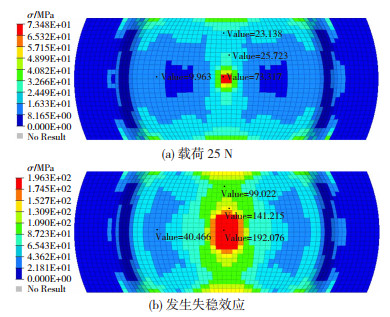
从成形深度16和24 mm试样应力结果(图 6、图 7)可以看出,试样最大应力位于试样的中心,与压头接触的位置。当载荷为25 N时,两种试样对应的最大应力分别为76和73 MPa,均未超过材料的屈服强度,材料处于弹性阶段,因此初始刚度与屈服强度无关。在本模型中,由于未考虑成形引起的厚度减薄,导致初始刚度仿真结果偏高,尤其对于成形深度24 mm的试样,其厚度减薄更加明显,初始刚度仿真结果与实验结果偏差更大。
|
图 6 成形深度16 mm试样的应力结果 Fig.6 Stress result of samples with a forming depth of 16 mm: (a) load is 25 N; (b) buckling effect occurs |
|
图 7 成形深度24 mm试样的应力结果 Fig.7 Stress result of samples with a forming depth of 24 mm: (a) load is 25 N; (b) buckling effect occurs |
失稳凹陷载荷不仅与厚度相关,还与材料屈服强度有关。试样发生失稳效应时,成形深度16和24 mm试样中心位置的应力分别为193和194 MPa,也就是说试样中心的应力达到材料屈服强度(193 MPa)后发生了失稳效应,说明失稳凹陷载荷与材料屈服强度有关[13]。材料在成形阶段会发生应变硬化,变形抗力增大,从而影响失稳凹陷载荷,因此有必要在仿真计算中考虑厚度减薄和应变硬化影响,从而提升失稳凹陷载荷精度。
3 成形-抗凹性能联合仿真 3.1 仿真分析方法为考虑成形引起的厚度减薄和应变硬化对抗凹性能的影响,本文联合成形和抗凹性能仿真。首先进行成形仿真分析,然后采用映射的方法将成形仿真结果中的厚度和应变信息传递到抗凹性能仿真计算中。具体步骤:在成形仿真时,通过Interface_Springback_Lsdyna关键字输出厚度和应变结果到dynain文件;建立抗凹有限元模型(2.1小节);分别在试样相同位置选择3个节点确定两个模型中试样的映射关系;通过Ls-dyna软件include_stamped_part关键字将dynain中的厚度和应变结果映射到抗凹有限元模型中,通过该关键字可以实现不同网格之间的映射。材料仍然采用MAT_PIECEWISE_LINEAR_PLASTICITY各向同性硬化模型。
3.2 成形仿真建模及结果 3.2.1 成形仿真建模利用三维软件设计了凸模和凹模(图 8),其中凸模表面的曲率半径为940 mm,圆角半径为13 mm,凹模圆角半径为13 mm。仿真参数设置:成形速度设定为100 mm/s,材料采用MAT_3-PARAMETER_BARLAT模型[14],凸模和凹模采用MAT_RIGID刚性材料模型,试样初始网格尺寸为5 mm,计算过程中网格自适应,为提升仿真精度,采用Belytschko-Tsay全积分壳单元方程。通过Interface_Springback_Lsdyna关键字输出结果到dynain文件,用于后续抗凹性能仿真。

|
图 8 成形仿真模型 Fig.8 Forming simulation model |
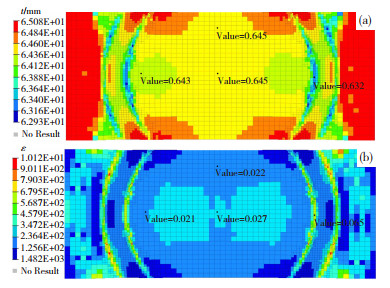
从图 9成形深度16 mm试样的厚度和塑性应变结果可以看出,试样中心区域的塑性应变为2.1%~2.7%,实际厚度为0.643~0.645 mm,减薄约0.006 mm,减薄率0.9%;试样圆角区域应变和减薄较大,如试样右侧圆角处塑性应变为6.5%,厚度为0.632 mm,减薄0.018 mm,减薄率2.8%。
|
图 9 成形深度16 mm试样的厚度(a)和塑性应变(b)结果 Fig.9 Thickness (a) and plastic strain (b) result of samples with a forming depth of 16 mm |
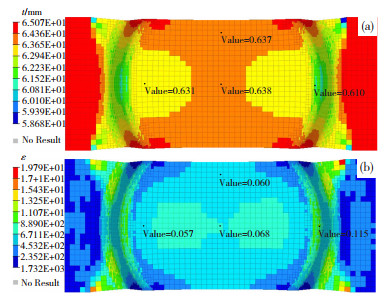
从图 10成形深度24 mm试样的厚度和塑性应变结果可以看出,试样中心区域塑性应变为5.7%~6.8%,厚度为0.631~0.638 mm,减薄约0.015 mm,减薄率2.3%;试样圆角区域应变和减薄较大,如试样右侧圆角处塑性应变为11.5%,厚度为0.61 mm,减薄0.04 mm,减薄率6.2%。
|
图 10 成形深度24 mm试样的厚度(a)和塑性应变(b)结果 Fig.10 Thickness (a) and plastic strain (b) result of samples with a forming depth of 24 mm |
通过Ls-dyna软件include_stamped_part关键字将成形仿真结果文件dynain中的厚度和应变结果映射到抗凹有限元模型中,再次计算初始刚度和失稳凹陷载荷,表 4为成形深度16和24 mm试样的初始刚度和失稳凹陷载荷仿真结果,初始刚度和失稳凹陷载荷仿真误差均<5%。
| 表 4 初始刚度和失效凹陷载荷仿真结果 Table 4 Simulation result of initial stiffness and buckling effect load |
成形深度16和24 mm试样中心位置最大塑性应变分别达2.7%和6.8%,通过与HC180BD+Z应力应变曲线(图 11)对比,两个塑性应变对应的材料强度分别为259.3和309.1 MPa。因为仿真模型采用的是各向同性硬化模型,因此试样中心位置材料的屈服强度也分别提高到259.3和309.1 MPa。

|
图 11 HC180BD+Z应力应变曲线 Fig.11 Stress-strain curve of HC180BD+Z |
图 12为成形深度16和24 mm试样发生失稳效应时的应力结果,其试样中心位置的应力分别为261和309 MPa,即试样中心的应力达到材料应变硬化后的屈服强度(259.3和309.1 MPa)后发生了失稳效应。结合前面数据,考虑应变硬化后材料屈服强度增加,试样更不容易发生失稳效应,从而失稳凹陷载荷的仿真结果增大。

|
图 12 发生失稳效应时的应力结果 Fig.12 Stress result when the buckling effect occurs: (a) 16 mm; (b) 24 mm |
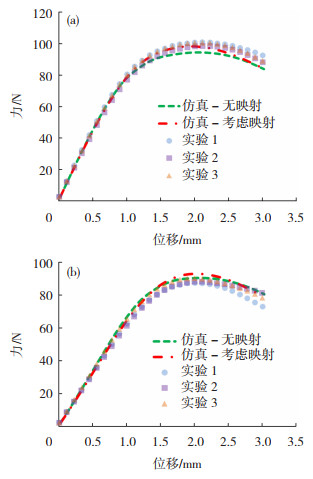
图 13为实验与两次仿真计算获得的力-位移曲线,其中“仿真-无映射”曲线为不考虑厚度减薄和应变硬化的计算结果,“仿真-考虑映射”曲线为采用厚度减薄和应变硬化映射方法的计算结果,两种方法获得的仿真曲线与实验曲线基本一致,但是采用映射方法的仿真结果显然更贴合实验曲线。
|
图 13 实验和仿真计算的力-位移曲线 Fig.13 Force-displacement curve of the test and simulation: (a) 16 mm; (b) 24mm |
表 5为初始刚度的实验和仿真结果,在不考虑厚度减薄时,成形深度24 mm试样的初始刚度为67.1 N/mm,仿真误差为7.8%,而考虑厚度减薄后初始刚度降低为64.4 N/mm,仿真误差减小到3.4%。可见,厚度是影响刚度的一个关键因素,不考虑成形引起的厚度减薄使得初始刚度计算结果偏高。
| 表 5 映射对初始刚度仿真结果的影响 Table 5 Effect of mapping on the results of initial stiffness |
失稳凹陷载荷的实验和仿真结果如表 6所示。通过映射方法考虑厚度减薄和应变硬化的影响后,成形深度16 mm试样的失稳凹陷载荷仿真误差从5.7%降低至1.8%,而成形深度24 mm试样仿真误差从2.0%增大到4.8%。采用映射方法后成形深度24 mm试样的失稳凹陷载荷仿真误差增大,主要原因为试样在成形、抗凹性能测试过程中受到复杂的应力加载历程,需要考虑材料Bauschinger效应[15]。而本文采用的各向同性硬化模型单一,不能获得真实的材料行为,采用该模型会高估材料的硬化强度,从而高估试样的失稳凹陷载荷。金属材料的真实硬化行为应该是各向同性硬化和随动硬化的混合模型[16-18],因此应该使用各向同性硬化和随动硬化的混合硬化模型来获得更加精确的仿真结果。
| 表 6 映射对失稳凹陷载荷仿真结果的影响 Table 6 Effect of mapping on the results of buckling effect loads |
本文采用MAT_PLASTIC_KINEMATIC混合硬化模型重新计算成形深度24 mm试样的失稳凹陷载荷。该模型采用双线性曲线近似描述材料的弹塑性,可描述各向同性硬化和随动硬化塑性模型。根据硬化系数β值的不同描述不同的硬化模型:β=0为随动硬化模型;β=1为各向同性硬化模型;0<β<1为混合硬化模型。MAT_PLASTIC_KINEMATIC模型的材料密度、弹性模量、泊松比采用表 2中的数据。该模型应力应变方程为
| σ=σ0+ET(ε−σ0/E) | (1) |
式中:σ为真实应力;σ0为屈服强度;ε为真实应变;ET为切线模量, E为弹性模量。将该方程转化为真实应力-塑性应变方程为
| σ=σ0+EPεP | (2) |
式中:Ep为塑性硬化模量且Ep=ETE/(E-ET);εp为真实塑性应变。本文将通过与HC180BD+Z应力应变曲线(图 14)对比获得合适的σ0和Ep值,然后计算出MAT_PLASTIC_KINEMATIC模型的参数ET。

|
图 14 应力应变曲线对比 Fig.14 Comparison of stress-strain curve |
从前面分析得出,试样发生失稳凹陷主要与试样中心位置的材料发生屈服有关,由3.2.2小节的成形仿真结果可知,成形深度24 mm试样中心区域的最大塑性应变为0.068,因此只需在0~0.068塑性应变范围内将公式(2)的曲线趋近HC180BD+Z应力应变曲线即可。HC180BD+Z应力应变曲线过(0,182.5)和(0.068,309.1)两个点,使公式(2)的曲线同样也经过这两个点(图 14),并计算出σ0为182.5 MPa,Ep为1 862 MPa,ET为1 846 MPa。最终获得了MAT_PLASTIC_KINEMATIC材料模型的参数。
本文采用以上MAT_PLASTIC_KINEMATIC材料模型,β分别取0、0.1、0.2等9个值重新计算了失稳凹陷载荷,获得了不同硬化系数的仿真结果(表 7)。结果显示:β=1时(各向同性硬化)失稳凹陷载荷仿真结果为93.07 N,与4.3小节采用MAT_PIECEWISE_LINEAR_PLASTICITY各向同性硬化模型计算的结果(93.1 N)基本一致,也说明在该抗凹仿真模型中采用MAT_PLASTIC_KINEMATIC材料模型具有一定的合理性;β=0时(随动硬化)失稳凹陷载荷仿真结果为86.27 N,低于实验结果(88.8 N);随着硬化系数的降低,随动硬化比重越大,失稳凹陷载荷仿真结果逐渐越低;β值为0.2时失稳凹陷载荷仿真结果(89.26 N)与实验结果(88.8 N)最吻合。
| 表 7 硬化系数β对失稳凹陷载荷仿真结果的影响 Table 7 Effect of hardening parameter on the results of buckling effect loads |
1) 未考虑成形引起的厚度减薄和应变硬化影响时,初始刚度和失稳凹陷载荷的仿真误差<10%,通过映射方法考虑成形引起的厚度减薄和应变硬化效应后,仿真误差<5%,仿真精度得到提升。
2) 初始刚度与材料厚度相关,与材料屈服强度无关,采用厚度映射的方法能够更加准确反映真实的试样厚度,因此能有效提升试样初始刚度的仿真精度。
3) 失稳凹陷载荷与材料厚度和材料强度均有关,成形引起的厚度减薄降低失稳凹陷载荷,而应变硬化提升材料屈服强度,有利于提升失效凹陷载荷。
4) 在采用厚度和应变映射后,成形深度24 mm试样的失稳凹陷载荷仿真误差增大,主要是由于采用了同向硬化模型导致的,采用更加合理的各向同性和随动混合硬化模型会得到更好的仿真结果。
| [1] |
李光霁, 刘新玲. 汽车轻量化技术的研究现状综述[J]. 材料科学与工艺, 2020, 28(5): 47-61. LI Guangji, LIU Xinling. Literature review on research and development of automotive lightweight technology[J]. Materials Science and Technology, 2020, 28(5): 47-61. DOI:10.11951/j.issn.1005-0299.20190232 |
| [2] |
陈晓辉, 金飞翔, 沈智, 等. 汽车覆盖件抗凹性能研究进展[J]. 材料导报, 2015, 29(8): 70-75. CHEN Xiaohui, JIN Feixiang, SHEN zhi, et al. The progress of the dent resistance of automotive body panels[J]. Materials Repots, 2015, 29(8): 70-75. DOI:10.11896/j.issn.1005-023X.2015.015.013 |
| [3] |
逯若东, 程超, 陈自凯, 等. DP490双相钢车门外板应用研究[J]. 锻压技术, 2020, 45(5): 110-115. LU Ruodong, CHENG Chao, CHEN Zikai. Research on DP490 dual phase steel application in door outer panel[J]. Forging and Stamping Technology, 2020, 45(5): 110-115. DOI:10.13330/j.issn.1000-3940.2020.05.019 |
| [4] |
ZHANG Yan, LAI Xinmin, ZHU Ping, et al. Lightweight design of automobile component using high strength steel based on dent resistance[J]. Materials and Design, 2006, 27(1): 64-68. DOI:10.1016/j.matdes.2004.09.010 |
| [5] |
汪承璞, 俞宁峰, 吴华, 等. 汽车钢板抗凹性实验研究[J]. 材料科学与工艺, 2004, 12(6): 623-629. WANG chengpu, YU Ningfeng, WU Hua, et al. Research on denting resistance testing for auto body sheet steel[J]. Materials Science and Technology, 2004, 12(6): 623-629. DOI:10.3969/j.issn.1005-0299.2004.06.017 |
| [6] |
STEFAN H, BABAK N. Numerical assessment of stiffness and dent properties of automotive exterior panels[J]. Materials and Design, 2004, 25(5): 361-368. DOI:10.1016/j.matdes.2003.12.005 |
| [7] |
张龙柱, 王连轩, 李晓广, 等. 汽车覆盖件用钢板的抗凹性能研究[J]. 热加工工艺, 2022, 51(7): 40-43. ZHANG Longzhu, WANG Lianxuan, LI Xiaoguang, et al. Research on dent resistance properties of steel sheets for automotive outer panel[J]. Hot Working Technology, 2022, 51(7): 40-43. DOI:10.14158/j.cnki.1001-3814.20200849 |
| [8] |
全国钢标准化技术委员会. 金属材料薄板和薄带抗凹性能试验方法: GB/T34477—2017[S]. 北京: 中国标准出版社, 2017.
|
| [9] |
中国汽车工程学会. 汽车覆盖件板材抗凹性能试验方法: SAE-China J3201—2013[S]. 北京: 中国汽车工程学会, 2013.
|
| [10] |
SHAIK S, RAJ A, MANIKANDAN G, et al. Prediction of forming strain for optimum dent resistance[J]. International Journal of Mechanical Engineering and Robotics Research, 2021, 10(11): 633-638. DOI:10.18178/IJMERR.10.11.633-638 |
| [11] |
杨雁文. 某车型汽车顶盖冲压成形与抗外压能力的研究[D]. 长春: 吉林大学, 2021. YANG Yanwen. Research on stamping and resistance to external pressure of automotive roof cover[D]. Changchun: Jilin University, 2021. |
| [12] |
俞祖俊, 张军, 陈新力, 等. 冲压成形对车身外覆盖件抗凹性影响研究[J]. 汽车工艺与材料, 2021, 36(1): 43-46. YU Zujun, ZHANG Jun, CHEN Xinli, et al. Study on influences of stamping on the dent resistance of automotive body outer panels[J]. Materials Science and Technology, 2021, 36(1): 43-46. DOI:10.19710/J.cnki.1003-8817.20200264 |
| [13] |
JAEHYUN K, HONGWOO L, KYUNGSEOK O, et al. Experimental and numerical investigation on the dent resistance of a dual phase steel originated from the yield-point phenomenon[J]. Journal of Materials Processing Technology, 2021, 289: 116929. DOI:10.1016/j.jmatprotec.2020.116929 |
| [14] |
赵坤民, 高岩, 赵德望, 等. 汽车用大型复杂冲压件拉延回弹仿真[J]. 塑性工程学报, 2021, 28(12): 12-20. ZHAO Kunming, GAO Yan, ZHAO Dewang, et al. Drawing springback simulation of large complex stamping part for automobile[J]. Journal of Plasticity Engineering, 2021, 28(12): 12-20. DOI:10.3969/j.issn.1007-2012.2021.12.002 |
| [15] |
SHEN Hongqing, LI Shuhui, CHEN Guanlong. Numerical analysis of panels' dent resistance considering the Bauschinger effect[J]. Materials and Design, 2010, 31(2): 870-876. DOI:10.1016/j.matdes.2009.07.043 |
| [16] |
RESAPU R, PERUMAHANTHI R. Numerical study of bilinear isotropic & kinematic elastic-plastic response under cyclic loading[J]. Materials Today: Proceedings, 2021, 39(4): 1647-1654. DOI:10.1016/j.matpr.2020.05.812 |
| [17] |
DANIEL C, ANDRÉ P, VASCO S, et al. Work hardening of metallic sheets under tension-compression and simple shear reverse loading[J]. Key Engineering Materials, 2022, 6392: 2012-2021. DOI:10.4028/P-73LQ3W |
| [18] |
CHEN Guang, ZHAO Changcai, SHI Haiwei, et al. Nonlinear kinematic hardening constitutive model based on Hill48 yield criterion and its application in reverse deep drawing[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2022, 44(10): 1-11. DOI:10.1007/S40430-022-03741-2 |
 2024, Vol. 32
2024, Vol. 32



