目前,对轻质结构构件的需求一直是航空航天中的主要关注点,具有高强度比和高刚度比的碳纤维复合材料已经慢慢取代了传统飞机结构中的铝合金材料[1-3]。为了获得更好的结构设计,尺寸优化、形状优化和拓扑优化等结构优化方法被研究并应用。拓扑优化是一种数学方法,拓扑优化设计区域体积为约束函数,以柔度最小为目标函数,改进特定设计空间中的材料排列来提高零件的机械性能[4-6]。然而,拓扑优化的结果通常是一些复杂的结构特征,它们在复杂设计中的应用受到传统方法的制造能力和高成本的限制,如热压罐、拉挤成型和树脂传递模塑(RTM)[7-8]。增材制造是逐层累积材料的制造技术,弥补了将几何复杂的拓扑优化零件转化为复合材料成型件的技术空白[9]。Uriondo和Klippstein等[10-11]已经尝试使用增材制造技术来制造无人飞行器(UAV)。热塑性材料的抗拉强度较低,大多数3D打印产品现在仍被用作概念模型来展示,而不是最终的功能性产品,因为通过3D打印制造的纯聚合物产品缺乏有效的机械性能,限制了其功能性应用[12-14]。复合材料的3D打印解决了以上这些问题,通过基质和增强材料的结合来构成一个系统,该系统具有任何单独的成分都无法获得的更有用的结构或功能属性[15-16]。Wang等[17]研究了颗粒增强和短纤维增强复合材料的不同增材制造技术,通过这种工艺生产的零件显示出与铝相当的性能。最常见的两种实现方式是在基质中填充短纤维或连续纤维,并已取得了相应的研究成果。Andrew等[18]在纯聚酰胺(PA)中添加短纤维,以悬臂梁为研究对象,并与纯树脂样品对比,发现短切纤维增强试样的机械强度明显提高。虽然短纤维相对于基础聚合物有了一定的提高,但连续碳纤维增强材料将聚合物性能提高了1~2个数量级[19-20]。连续碳纤维增材制造的优势在于,可以有选择地增强零件的某个部位,通过在最需要强度的地方添加连续纤维,精确地调整零件的强度剖面。
本文利用3D打印技术制备了“椭圆形跑道”样件,主要研究了不同纤维角度和纤维层分布对样件力学性能的影响,并观察了样件的断裂模式,然后采用拓扑优化对样件进行优化设计,并通过三点弯曲梁、C形夹和弹架悬臂试件进行了验证。
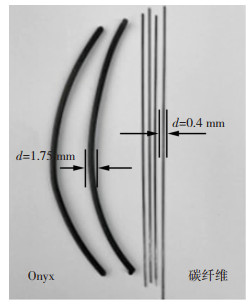
1 纤维铺设方式对成型件力学性能的影响 1.1 原材料使用的材料为Markforged提供的专用预浸碳纤维和Onyx基材,其中碳纤维线径0.4 mm,Onyx基材线径1.75 mm,如图 1所示。
|
图 1 原材料 Fig.1 Raw materials |
其中Onyx是将韧性尼龙与一种短切碳纤维所做成的复合基材,它的强度和硬度是ABS的1.6倍,并减少了收缩和翘曲。预浸长纤维丝束由多股涂有尼龙基质的碳纤维组成,纤维轴向上的力学性能如表 1所示。
| 表 1 碳纤维复合材料的力学性能 Table 1 Mechanical properties of carbon fiber composites |
本文研究使用的设备是Mark Two 3D打印机,如图 2所示。该打印机带有一个双喷嘴系统的打印头,打印参数如表 2所示。Onyx基材被熔化成大约1 mm宽和0.125 mm厚的路径。

|
图 2 Mark Two 3D打印机 Fig.2 Mark Two 3D printer |
| 表 2 打印参数 Table 2 Printing parameters |
本实验使用的双喷嘴3D打印机工作原理如图 3所示。双喷嘴独立工作,分别打印预浸制连续纤维和Onyx基质。打印线材通过送丝装置传送到加热装置中,在加热装置中将材料加热至熔融状态并通过打印喷嘴将其挤出,喷嘴在打印平台上的水平移动来完成熔融丝的有序沉积,从而在同一水平面上构建一个完整的打印层。在连续纤维层中,先使用连续碳纤维复合材料进行填充,然后使用Onyx基质将空缺部分填充完整。

|
图 3 双喷嘴3D打印原理图 Fig.3 Dual nozzle 3D printing schematic |
连续碳纤维具有各向异性的特点,其中纤维方向具有较高的强度和刚度,而跨层方向具有较低的强度和刚度。Goh等[21]研究了连续碳纤维在x、y和z方向上对拉伸、压缩和弯曲性能的影响,其中x方向的拉伸强度比z方向上的拉伸强度提高了15 031%,x方向的压缩强度比z方向上的压缩强度提高了242.9%,xy方向上的剪切强度比xz和yz方向上的剪切强度分别提高了373.7%、251.6%。因此接下来本文主要研究xy层上纤维方向对样件力学性能的影响。
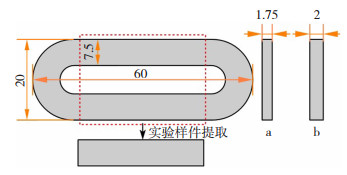
如图 4所示,样件成“椭圆形跑道”,以允许从每个试样中提取多个单向样品进行拉伸、压缩和三点弯曲试验。其中样件a、b的厚度分别为1.75和2 mm,可打印层数分别为14层和16层,2种样件在打印过程中都会有0.125 mm厚的底层和顶层是用Onyx进行填充,以保证上下面的光洁度。
|
图 4 连续碳纤维打印样件(单位:mm) Fig.4 Continuous carbon fiber print specimen |
样件a的连续纤维层采用“同心”纤维路径铺设,基材使用三角形路径打印,其中碳纤维层中连续纤维共4圈,内外墙各铺设2圈,如图 5所示。

|
图 5 椭圆形跑道碳纤维层铺设方式 Fig.5 The laying method of carbon fiber layer for oval racetrack |
本样件中打印层共14层,其中碳纤维层数为6,打印过程中底层和顶层各铺设2层Onyx基材,其余打印层的分布方式如图 6所示。图 6(a)中碳纤维层全部分布在顶端;图 6(b)碳纤维层均匀分布在上下两端;图 6(c)碳纤维层均匀分布在上、中、下;图 6(d)碳纤维层采用间隔的分布方式。

|
图 6 碳纤维层的分布方式 Fig.6 The distribution of carbon fiber layers |
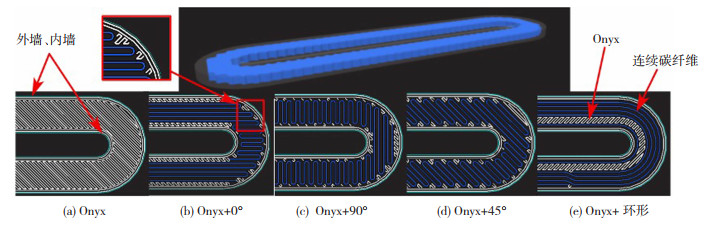
样件b打印层共16层,底层和顶层各铺设2层纯基材,其余打印层全部采用不同角度的碳纤维填充。图 7是0°和90°交叉铺设。图 8(a)全部采用Onyx填充;图 8(b)的纤维角度为0°;图 8(c)的纤维角度为90°;图 8(d)的纤维角度为45°;图 8(e)采用同心纤维的铺设路径。虽然纤维层中的纤维角度不同,但在设置过程中会保证不同角度的纤维层中的连续碳纤维含量是相同的。

|
图 7 0°和90°交叉铺设 Fig.7 0° and 90° cross laying |
|
图 8 不同角度的碳纤维铺设路径 Fig.8 Different angles of carbon fiber laying paths |
图 9为椭圆形的打印样件,将上述不同纤维路径制造的椭圆形样件分别取一段在UTM4204型电子材料试验机上做拉伸、压缩和弯曲力学性能测试,装置设置如图 10所示。其中,拉伸试验标距25 mm,加载速度2 mm/min,当样件断裂时实验结束,计算标准为GB/T 1447—200。压缩试验标距10 mm,加载速度2 mm/min,由于压缩试样较小,在压缩过程中破裂现象不明显,计算标准为GB/T 1448—2005。弯曲试验跨距35 mm,加载速2 mm/min,计算标准为GB/T 1449—2005。

|
图 9 椭圆形打印样件 Fig.9 Oval print sample |

|
图 10 样件力学性能测试 Fig.10 Mechanical properties testing of sample parts: (a) the tensile test; (b) the compression test; (c) three-point bending test |
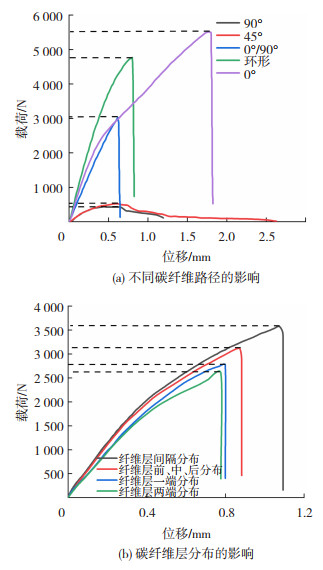
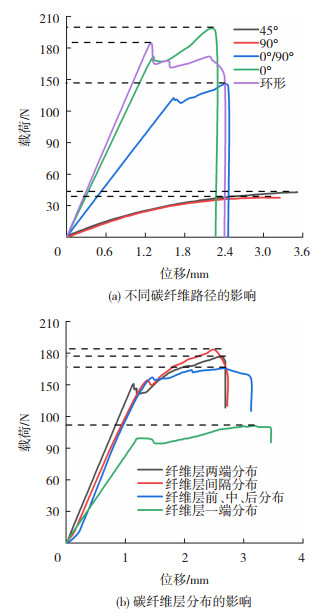
连续碳纤维不同铺设方式的拉伸载荷-位移曲线如图 11所示。从图 11(a)中可以看出,0°碳纤维铺设峰值载荷为5 513 N,而90°碳纤维铺设峰值载荷仅为427 N,约为0°铺设路径的1/13。45°和90°纤维铺设的样件仅有塑性变形阶段,而0°、0°/90°和环形纤维铺设的样件的失效方式为断裂。这是因为连续纤维增强复合材料被设计用来承受纤维方向的载荷,横向载荷可能导致早期失效。
|
图 11 连续碳纤维铺陈对拉伸强度的影响 Fig.11 Effect of continuous carbon fiber laydown on tensile strength: (a) effect of different carbon fiber paths; (b) effect of carbon fiber layer distribution |
从图 11(b)可以看出,当碳纤维层仅分布在样件的某一端面时,承载力为2 596 N,而当碳纤维层间隔分布时,最大承载力为3 573 N,比分布在某一端面时的峰值载荷约提高了37.6%。从这4种不同纤维层的峰值载荷可以得出,当碳纤维层分布排列越均匀时,样件所承受的最大拉伸载荷越大。
1.3.2 连续碳纤维路径对压缩强度的影响连续碳纤维不同铺设方式的压缩载荷-位移曲线如图 12所示。碳纤维复合材料样件在压缩实验过程中的主要失效模式是层间剪切,这是因为在3D打印的过程中喷嘴在层间的压力比较小而导致高空隙率,进而形成碳纤维与基体层之间的不良粘合。从图 12(a)可以看出90°纤维铺设时的最大承载力为694 N,而0°和环形路径铺设时的最大承载力分别为1 659和1 893 N,比90°铺设时分别提高了153.67%和172.77%。由于碳纤维各向异性的特点,在纤维方向具有较高的强度和刚度,45°和90°纤维铺设与压缩方向存在一定的角度,在压缩过程中纤维会受到弯曲力和剪切力,从而导致样件的过早失效。

|
图 12 续碳纤维铺陈对压缩强度的影响 Fig.12 Continued effect of carbon fiber laydown on compression strength: (a) effect of different carbon fiber paths; (b) effect of carbon fiber layer distribution |
从图 12(b)可以看出,在研究碳纤维层分布方式对压缩强度的影响时,最大承载件是碳纤维层间隔分布(1 704 N),最小承载件为碳纤维层在样件中前、中、后均匀分布(1 310 N),两者仅相差394 N。结合图 12可以得出,在压缩试验时,碳纤维的铺设角度对样件的压缩性能影响占主要因素,而碳纤维层的分布对样件的压缩强度影响较小。
1.3.3 连续碳纤维路径对弯曲强度的影响连续碳纤维不同铺设方式的三点弯曲载荷-位移曲线如图 13所示,从图 13(a)可以看出,碳纤维角度为90°时的最大承载力为37 N,而碳纤维角度为0°时的最大承载力为194 N,比最小承载力提高了424%。0°和环形的碳纤维方向在弯曲实验中基本一致,根据实验数据来看,两者的峰值载荷仅相差10 N。在0°、0°/90°和环形纤维样件弯曲过程中,由于垂直于弯曲方向的连续碳纤维丝拉扯作用导致最大承载力增大,而45°和90°碳纤维样条在三点弯曲实验中,垂直于弯曲方向基本无连续碳纤维,此时弯曲面相当于只有基材Onyx,因而仅发生塑性变形而没有发生断裂。
|
图 13 续碳纤维铺陈对三点弯曲强度的影响 Fig.13 Continued effect of carbon fiber laydown on three-point bending strength: (a) effect of different carbon fiber paths; (b) effect of carbon fiber layer distribution |
从图 13(b)可以看出,当碳纤维层仅分布在样件的一端时,承载力仅为111 N,而碳纤维层间隔均匀分布时的承载力为182 N,比最小承载力提高了64.0%。通过观察不同碳纤维层样件的峰值载荷的变化趋势可以得出,当碳纤维层在样件的两端外表面分布越均匀时,弯曲载荷的峰值越高。
2 基于变密度的结构拓扑优化拓扑结构优化设计中,结构部件柔度的最小化(刚度的最大化)定义为初始设计目标,将体积分数设置为约束条件,用于确定最佳材料分布的相对密度定义为设计变量,并且其材料参数和密度之间存在着连续变量的函数对应关系,材料的密度可在区间[0, 1]取值[22]。假设材料是各向同性的,最小化柔度C的拓扑优化数学模型表示如下所示:
| $ \left\{\begin{array}{l} \text { Find: } x=\left(X_i, X_2, \cdots, X_i\right), \quad i=1, 2, \cdots, n \\ \operatorname{Min}: C(x)=\boldsymbol{F}^T U=\boldsymbol{U}^T K u \\ \text { Subject to }: f=V^* / V \\ 0<X_{\min } \leqslant X_n \leqslant 1, \quad i=1, 2, \cdots, n \end{array}\right. $ |
式中:Xi为设计变量,代表离散单元的相对密度,取值为[0, 1]之间的连续值,n代表设计变量个数,为了避免总刚度矩阵奇异,取Xmin=0.001[23];C(x) 为目标函数;C为结构的柔顺度,Cmin表示结构刚度最大;K为总体刚度矩阵;U为总体位移矢量;F为结构所受载荷矢量;f为给定材料体积比;V为整体结构体积;V*为优化后的结构体积。
当拓扑优化模型的伪密度值在[0, 1]内任意连续取值时,若求解后单元的密度为0,则此处单元可以完全去除材料;若求解后单元的密度等于1,此处单元为实体;若密度在0.5附近,则需引入惩罚因子P对中间值进行惩罚,使其更快的向0和1两端偏移[24-25]。
拓扑优化是在给定的设计区域内,根据约束条件,已知载荷及界条件,如图 14,经过拓扑优化分析寻找到该零件的最佳结构分布如图 15,在满足结构刚度的前提下,减轻结构重量,以实现结构的轻量化设计。

|
图 14 初始设计区域 Fig.14 Initial design area |

|
图 15 拓扑优化结果 Fig.15 Topology optimization results |
图 16是C形夹的设计域及拓扑优化过程,左端面仅固定x和y方向,在右端口处分别向上/下施加载荷。优化部件的总厚度为5 mm,使用尺寸为1 mm×1 mm的四边形四节点正方形单元的精细网格方法对设计域进行离散化。整个结构的柔度最小化为设计目标,而材料体积分数设为约束条件,其中体积分数f=0.2。
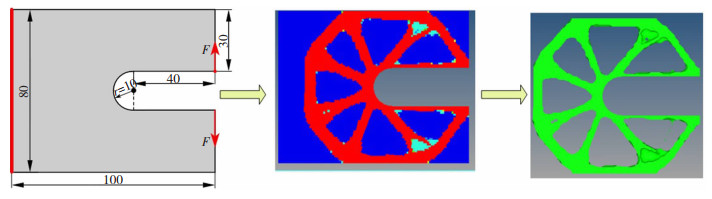
|
图 16 C形夹设计区域及拓扑优化过程(单位: mm) Fig.16 C-clip design area and topology optimization process |
在制备打印件时要经过结构拓扑优化和打印制造两个步骤,图 17为连续碳纤维增强复合材料结构件的拓扑设计和3D打印流程图。在拓扑优化过程中,根据零件载荷和工况创建相应的设计变量、约束条件和目标函数,并选择合适的最小成员尺寸和惩罚因子以获得拓扑收敛体。在制造过程中,首先根据拓扑优化后的结构创建适合加工的三维模型,然后设置适合的打印参数和连续纤维铺设路径将样件制造出来。
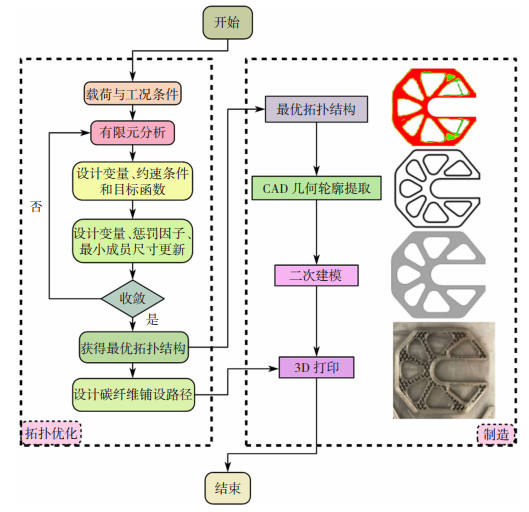
|
图 17 连续碳纤维增强复合材料结构件的拓扑设计和3D打印流程图 Fig.17 Topology design and 3D printing flow chart of continuous carbon fiber reinforced composite structural parts |
图 18为用于拉伸测试的不同碳纤维路径的3D打印C形夹构件。5个复合材料3D打印件的碳纤维路径分别是Onyx、Onyx+0°连续碳纤维、Onyx+45°连续碳纤维、Onyx+90°连续碳纤维、Onyx+环形连续碳纤维。

|
图 18 不同碳纤维路径的C形夹3D打印件 Fig.18 C-clamp 3D printed parts with different carbon fiber paths |
采用UTM4204型万能材料试验机进行C形夹结构件的拉伸实验,拉伸速率为10 mm/min,计算标准参照GB/T 1447—2005。图为C形夹样件的拉伸载荷-位移曲线。仅有Onyx基质的样件具有最低的峰值载荷(2 710 N),而具有连续碳纤维的样件中具有最高的峰值载荷的是纤维角度为90°的样件,大小为5 022 N,比只使用Onyx基质样件的峰值载荷提高了85.3%。5个样件的加载过程相似,在拉伸初始阶段为弹性变形,随着载荷逐渐增大,分别到达各自的峰值载荷后,发生断裂失效。
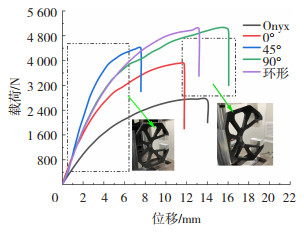
|
图 19 C形夹样件的载荷-位移曲线 Fig.19 Load-displacement curve of C-clamp sample |
当C形夹样件施加的载荷变成从两端向中间压缩时,将优化结构的厚度设计为10 mm,图 20是C形夹的设计域及结构拓扑优化过程,左端面仅固定x和y方向,在右端口两端向中间加压。
|
图 20 C形夹设计区域及拓扑优化过程(单位: mm) Fig.20 C-clamp design area and topology optimization process |
图 21为用于压缩测试的不同碳纤维路径的3D打印C形夹构件,5个复合材料3D打印件是由Onyx、Onyx+0°连续碳纤维、Onyx+45°连续碳纤维、Onyx+90°连续碳纤维、Onyx+环形连续碳纤维组成。

|
图 21 不同碳纤维路径的C形夹3D打印件 Fig.21 C-clamp 3D printed parts with different carbon fiber paths |
采用UTM4204型万能材料试验机进行C形夹结构件的压缩试验,压缩速率为10 mm/min,计算标准参照GB/T 1448—2005。图 22为C形夹压缩样件的载荷-位移曲线。仅有Onyx基质的样件具有最低的峰值载荷(1 469 N),而具有连续碳纤维的样件中环形铺设的样件峰值载荷为5 727 N,比只使用Onyx基质样件的峰值载荷提高了289.9%。初始都为弹性变形阶段,各个样件随着载荷逐渐增大,分别到达各自的峰值载荷后,发生断裂失效。
|
图 22 C形夹压缩试样的载荷-位移曲线 Fig.22 Load-displacement curve of C-clamp compression sample |
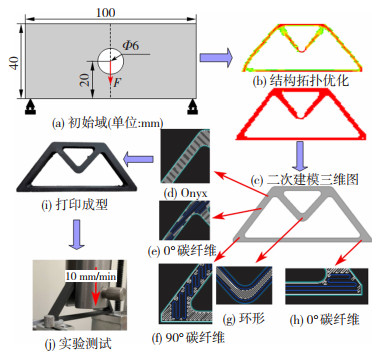
图 23为三点弯曲梁的结构拓扑优化设计、制造和实验测试过程,其中图 23(a)为三点弯曲梁的初始设计域、载荷和边界条件,在几何中心有一个直径为6 mm的圆形孔,用于在孔的底部边缘中心承受集中载荷。在梁的两个底端仅固定z方向。使用尺寸为1 mm×1 mm的四边形四节点正方形单元的精细网格方法对设计域进行离散化,整个结构的柔度最小化为设计目标,材料体积分数设为约束条件,其中体积分数f=0.2,即各向同性材料的总重量减少至少80%,拓扑优化迭代过程如图 23(b)所示。拓扑优化后的结构锯齿点较多,不满足制造条件。基于优化后的结构,结合增材制造零件的设计准则,对零件重新建模如图 23(c)所示。图 23(d)~(h)是在保证碳纤维含量一致的情况下不同纤维路径的铺设方式。制造出来的样件如图 23(i),在拉伸机上进行力学性能的测试,测样件安装情况如图 23(j)所示。根据设计边界条件,截面的两个底端由固定滚轮支撑,压缩加载销施加在三点弯曲试样的中心开孔上,位移速率为10 mm/min。
|
图 23 三点弯曲梁的结构拓扑优化设计、制造和实验测试过程 Fig.23 Process of structural topology optimization design, fabrication and experimental testing of three-point bending beams |
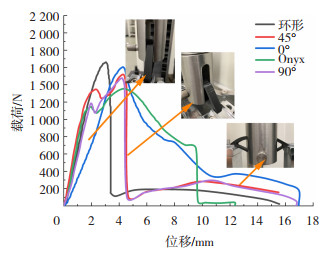
三点弯曲样件的载荷-位移曲线如图 24所示。
|
图 24 三点弯曲梁的载荷-位移曲线 Fig.24 Load-displacement curves of three-point bending beams |
由图 24可以看出,当位移达到约4.2 mm时,样件的载荷迅速增加至峰值,最大值是环形铺设方式,数值为1 660 N;最小值为纯Onyx基质,数值为1 352 N,两者仅相差308 N。差值较小的原因与本实验铺设连续碳纤维含量过少有一定的关系。达到峰值后,样件的载荷由于上部框架的开裂而下降,然后载荷由于大面积开裂而急剧下降。
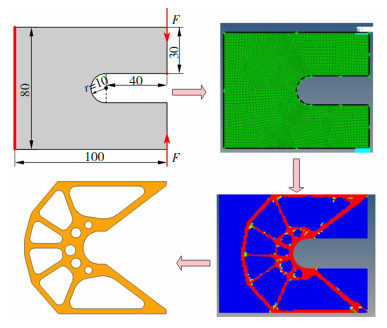
2.3 弹架悬臂拓扑优化弹架悬臂是航空器上的重要构件,在结构上应足够坚固,以抵抗在工作时的瞬时冲击和磨损,并且足够轻,以便战斗机可以具有更长的续航能力,而普通的热塑性塑料强度不足以承受这种冲击。因此,可基于结构拓扑优化和连续碳纤维3D打印制造出兼顾结构和重量的弹架悬臂。弹架悬臂结构的拓扑优化设计过程如图 25所示,首先在几何形状简单的材料块上定义边界和载荷条件如图 25(a)所示,在拓扑优化过程中将从该材料块上移除材料。弹架悬臂的底部是简单支撑的,在结构右端八个通孔处施加垂直向下的载荷。选择优化区域进行网格划分,本文共划分90 364个网格,如图 25(b)所示。以体积分数f=0.2为约束条件,最小柔度为目标函数进行拓扑优化,最终优化结果如图 25(c)所示。由于拓扑优化所得到的结构通常是不平滑和不连续的,在保证原始轮廓尺寸的前提下并结合3D打印结构设计准则通过使用三维建模软件对拓扑优化算法生成的结构重新建模,如图 25(d)所示。并对建模后的三维模型再次受力分析,如图 25(e)所示。结合上文中不同的纤维路径对机械性能的影响和受力云图进行纤维路径的设计,最终打印件如图 25(f)所示。

|
图 25 弹架悬臂拓扑优化设计流程 Fig.25 Topology optimization design process of the bullet rack cantilever |
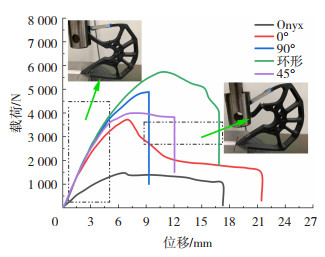
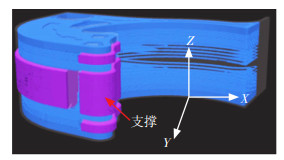
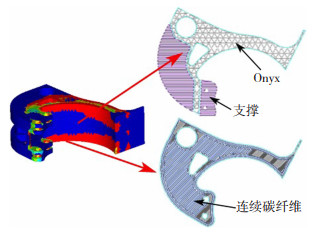
弹架悬臂结构打印切片模型如图 26所示,其中紫色为支撑,其余为打印层,共有236层,连续碳纤维的使用量为11.31 cm3,总打印时间约为10.5 h。在图 27中,根据受力云图选择性的铺设连续纤维增强复合材料,连续纤维的特定放置将极大地提高部件的强度。本文所使用的铺设方法以较少量的连续纤维增强材料显著提高弹架悬臂的机械性能,如图 27所示。
|
图 26 打印切片模型 Fig.26 Printed slice model |
|
图 27 连续碳纤维铺设方式 Fig.27 Continuous carbon fiber laying |
弹架悬臂结构试验装置如图 28所示,使用直径为3 mm长度为55 mm金属杆穿过右端的通孔。采用UTM4204型万能材料试验机进行弹架悬臂结构的压缩试验,压缩速率为10 mm/min,计算标准参照GB/T 1448—2005。

|
图 28 弹架悬臂测试装置 Fig.28 Test device for bullet rack cantilever |
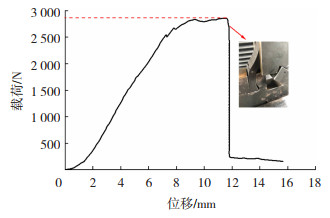
图 29为弹架悬臂压缩测试的载荷-位移曲线,当弹架悬臂位移为11.58 mm时,压缩载荷峰值为2 854 N。压缩过程中先发生弹性形变,当达到压缩载荷峰值后发生断裂而失效,载荷迅速降低。断裂部位如图 30所示,在此处发生断裂是因为在铺设连续碳纤维时,此部位宽度过窄,而导致此处连续纤维含量过少。
|
图 29 弹架悬臂载荷-位移曲线 Fig.29 Load-displacement curve of bullet rack cantilever |

|
图 30 弹架悬臂断裂处 Fig.30 Bullet rack cantilever fracture |
1) 研究了连续碳纤维角度对样条力学性能的影响。在拉伸试验中由于纤维增强复合材料被设计用来承受纤维方向的载荷,所以碳纤维角度为0°的样条比90°的样条最大承载力提高了1 191.1%。在压缩试验中,0°和环形碳纤维样条的最大承载力比90°的样条分别提高了153.67%和172.77%。45°和90°纤维铺设与压缩方向存在一定的角度,在压缩过程中纤维会受到弯曲力和剪切力,从而导致样件的过早失效。在样条三点弯曲试验中,连续碳纤维铺角度为0°的样条比90°的样条最大承载力提高了193%。
2) 研究了碳纤维层的分布对样件力学性能影响,发现碳纤维层的分布对压缩性能的影响较小。在拉伸试验中,从最大承载力变化的趋势可知,当碳纤维层分布越均匀时,样条所能承受的最大拉伸载荷越大,其中碳纤维层均匀分布比分布在某一端面时的最大承载力约提高了37.6%。在弯曲试验中,碳纤维层在样条的两端分布越均匀时,弯曲载荷越高,碳纤维层均匀分布和两端分布比碳纤维层一端分布弯曲载荷分别提高了64%和60.4%。
3) 在C形夹的拉伸、压缩试验中,具有连续碳纤维的样件峰值载荷比纯Onyx基质的样件分别提高了85.3%和289.9%,其中90°和环形铺设连续碳纤维样件表现比较优异,这是由于90°连续碳纤维与拉伸、压缩方向一致。而在三点弯曲样件中,0°和环形铺设的连续碳纤维样件表现比较优异。
4) 结构优化后的弹架悬臂结构能够承受2 854 N的载荷才发生断裂失效,这意味着弹架悬臂在实际应用中不会受到明显的压缩损伤。
本文揭示了3D打印复合材料具有显著的优异性,并证明了在适当的科学方法和创新设计的支持下,3D打印技术为航空航天工业制造高性能优化部件是可能的。
| [1] |
YEONG W Y, GUO D G. 3D printing of carbon fiber composite: The future of composite industry[J]. Matter, 2020, 2(6): 1361-1363. DOI:10.1016/j.matt.2020.05.010 |
| [2] |
KROLL E, ARTZI D. Enhancing aerospace engineering students' learning with 3D printing wind-tunnel models[J]. Rapid Prototyping Journal, 2011, 17(5): 393-402. DOI:10.1108/13552541111156522 |
| [3] |
BARILE C, CASAVOLA C, DE C F. Mechanical comparison of new composite materials for aerospace applications[J]. Composites, 2019, 1(Apr.1): 122-128. DOI:10.1016/j.compositesb.2018.10.101 |
| [4] |
YE M L, GAO L, LI H. A design framework for gradually stiffer mechanical metamaterial induced by negative Poisson's ratio property[J]. Materials & Design, 2020, 192: 108751. DOI:10.1016/j.matdes.2020.108751 |
| [5] |
SHA Wei, ZHAO Yiting, GAO Liang, et al. Illusion thermotics with topology optimization[J]. Journal of Applied Physics, 2020, 128(4): 045106. DOI:10.1063/5.0007354 |
| [6] |
LUO Yunfeng, LI Quhao, LIU Shutian. Topology optimization of shell-infill structures using an erosion-based interface identification method[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 355: 94-112. DOI:10.1016/j.cma.2019.05.017 |
| [7] |
CAMINERO M A, CHACON J M, GARCIA-MORENO I, et al. Interlaminar bonding performance of 3D printed continuous fibre reinforced thermoplastic composites using fused deposition modelling[J]. Polymer Testing, 2018, 68: 415-423. DOI:10.1016/j.polymertesting.2018.04.038 |
| [8] |
陈威, 张秋菊. 连续纤维增强热塑性复合材料3D打印研究进展[J]. 材料科学与工艺, 2022, 30(1): 21-34. CHEN Wei, ZHANG Qiuju. Research progress on 3D printing of continuous fiber reinforced thermoplastic composites[J]. Materials Science and Technology, 2022, 30(1): 21-34. DOI:10.11951/j.issn.1005-0299.20210096 |
| [9] |
PARANDOUSH P, LIN Dong. A review on additive manufacturing of polymer-fiber composites[J]. Composite Structures, 2017, 182(Dec.15): 36-53. DOI:10.1016/j.compstruct.2017.08.088 |
| [10] |
URIONDO A, ESPERON-MIGUEZ M, PERINPANAYAGAM S. The present and future of additive manufacturing in the aerospace sector: A review of important aspects[J]. Proceedings of the Institution of Mechanical Engineers, 2015, 229(11): 2132-2147. DOI:10.1177/0954410014568797 |
| [11] |
KLIPPSTEIN H, SANCHEZ A D D, HASSANI H, et al. Fused deposition modeling for unmanned aerial vehicles (UAVs): A review[J]. Advanced Engineering Materials, 2018, 20(2): 1700552. DOI:10.1002/adem.201700552 |
| [12] |
O'CONNOR H J, DOWLING D P. Low-pressure additive manufacturing of continuous fiber-reinforced poly mercomposites[J]. Polymer Composites, 2019, 40(11): 329-4339. DOI:10.1002/pc.25294 |
| [13] |
JUSTO J, TAVARA L, GARCIA-GUZMAN L, et al. Characterization of 3D printed long fibre reinforced composites[J]. Composite Structures, 2018, 185(Feb.2): 537-548. DOI:10.1016/j.compstruct.2017.11.052 |
| [14] |
NAKAGAWA Y, MORI K, MAENO T. 3D printing of carbon fibre-reinforced plastic parts[J]. International Journal Additive Manufacturing, 2017, 91(5-8): 2811-2817. DOI:10.1007/s00170-016-9891-7 |
| [15] |
SUGIYAMA K, MATSUZAKI R, UEDA M, et al. 3D printing of composite sandwich structures using continuous carbon fiber and fiber tension[J]. Composites, Part A-Applied Science and Manufacturing, 2018, 113: 114-121. DOI:10.1016/j.compositesa.2018.07.029 |
| [16] |
QUAN Chao, HAN Bin, HOU Zhanghao, et al. 3D printed continuous fiber reinforced composite auxetic honeycomb structures[J]. Composites, Part B-Engineering, 2020, 187(Apr.15): 107858. DOI:10.1016/j.compositesb.2020.107858 |
| [17] |
WANG Xin, JIANG Man, ZHOU Zuowan, et al. 3D printing of polymer matrix composites: A review and prospective[J]. Composites, Part B-Engineering, 2017, 110(Feb.1): 442-458. DOI:10.1016/j.compositesb.2016.11.034 |
| [18] |
ANDREW N D, JAMES N B, KEVIN A M, et al. Fabrication of continuous carbon, glass and kevlar fibre reinforced polymer composites using additive manufacturing[J]. Additive Manufacturing, 2017, 16146-16152. DOI:10.1016/j.addma.2017.06.004 |
| [19] |
VAN D W N, TEKINALP H, KHANBOLOUKI P N, et al. Additively manufactured carbon fiber-reinforced composites: State of the art and perspective[J]. Additive Manufacturing, 2020, 31: 100962. DOI:10.1016/j.addma.2019.100962 |
| [20] |
VAN DE WERKEN N, HURLEY J, SARVESTANI A N, et al. Design considerations and modeling of fiber reinforced 3D printed parts[J]. Composites, Part B-Engineering, 2019, 160(Mar.1): 684-692. DOI:10.1016/j.compositesb.2019.107681 |
| [21] |
GOH G D, TOH W, YAP Y L, et al. Additively manufactured continuous carbon fiber reinforced thermoplastic for topology optimized unmanned aerial vehicle structures[J]. Composites, Part B-Engineering, 2021, 216(July.1): 108840. DOI:10.1016/j.compositesb.2021.108840 |
| [22] |
张国锋. 基于变密度法的结构拓扑优化敏度过滤及后处理方法研究[D]. 成都: 四川大学, 2021. ZHANG Guofeng. Research on sensitivity filtering and post-processing methods for structural topology optimization based on variable density method[D]. Chengdu: Sichuan University, 2021. |
| [23] |
李好. 基于变密度法的连续体结构拓扑优化方法研究[D]. 武汉: 华中科技大学, 2011. LI Hao. Research on topology optimization method of continuum structure based on variable density method[D]. Wuhan: Huazhong University of Science and Technology, 2011. |
| [24] |
董莉, 吴晓明. 基于变密度法的多材料与结构一体拓扑优化研究[J]. 机电工程, 2020, 37(9): 1109-1114. DONG Li, WU Xiaoming. Topology optimization of multi-material and structure based on variable density method[J]. Mechanical and Electrical Engineering, 2020, 37(9): 1109-1114. DOI:10.3969/j.issn.1001-4551.2020.09.021 |
| [25] |
王景良, 朱天成, 朱龙彪, 等. 连续体结构的变密度拓扑优化方法研究[J]. 工程设计学报, 2022, 29(3): 279-285. WANG Jingliang, ZHU Tiancheng, ZHU Longbiao, et al. Study on variable density topology optimization for continuum structures[J]. Journal of Engineering Design, 2022, 29(3): 279-285. DOI:10.3785/j.issn.1006-754X.2022.00.039 |
 2024, Vol. 32
2024, Vol. 32


