2. 华南理工大学 机械与汽车工程学院,广州 510640;
3. 佛山市南海蕾特汽车配件有限公司,广东 佛山 528244
2. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, China;
3. Foshan Nanhai Lei Te Automotive Parts Co., Ltd., Foshan 528244, China
近年来,随着工业社会的进步和发展,轻量化零件已成为板料成形领域的研究热点。铝合金薄板因具有密度小、强度高等特点而成为最热门的轻量化材料之一,但其在冲压成形过程中极容易出现起皱、开裂等质量缺陷。为了分析铝合金圆锥形件的侧壁起皱机理,专家学者做了大量研究。Dick等[1]研究了材料特性对铝合金锥形件侧壁起皱幅值的影响,结果表明材料的各向异性会促进起皱的发生,而较低的屈服应力可降低起皱幅值。Neto等[2]利用数值模拟和实验对比的方法研究了网格质量、材料本构模型、工具体几何形状和摩擦系数对起皱幅值的影响,结果表明料片的有限元网格质量是准确预测侧壁起皱行为的关键。Oide等[3]利用静态隐式分析和人工阻尼相结合的方法,分析了采用弹塑性薄壳单元的圆锥形件局部起皱行为并评估了起皱区域的有效宽度。高亚南等[4]对绕弯成形特性进行研究, 并通过优化截面特征减小了成形后两侧面的宽度差,通过优化产品截面得出增强壁厚的方式不能够抵抗成形过程中立筋向内倒塌的趋势;采取增加微小凸台的方法,使得成形后右侧面宽度差减少。朱英霞等[5]提出基于ABAQUS/Explicit平台建立了铜钛双金属复合管绕弯- 回弹有限元模型,并通过实验验证了模型的可靠性,提出了一种适用于多种管材、多尺寸研究的数学模型。以上研究虽然分析了相关因素对数值模拟精确度和起皱幅值的影响程度,但未涉及解决铝合金薄板侧壁起皱的问题。
Tanongsak等[6]研究认为起皱行为是板料成形中最常见的失效形式之一,在炊具制造的拉深成形过程中经常发生,利用改进的Yoshida屈曲试验的实验和数值模拟所开发的起皱极限曲线(WLCs)准确预测了AA5054 - O和AA5052 - H32铝合金板材矩形杯形件拉深起皱行为。Sun等[7]研究了充液成形铝合金整流罩侧壁起皱机理及抑制方法,提出临界应变是起皱的评价指标,临界应变的大小和幅值可以定性分析起皱趋势,并从几何角度研究了材料流动趋势,预测了起皱发生的可能性。李振杰[8]在半球形冲压件起皱因素的分析中对宽凸缘半球形件的凸缘起皱和球面起皱机理进行了理论分析和有限元仿真,研究中采用增加压边力和毛坯直径可消除凸缘起皱; 增加压边力、增大毛坯直径、增加摩擦系数和采用圆形毛坯措施可以抑制球面起皱的发生。
本文以铝合金圆锥形件为研究对象,以最小起皱幅值为优化目标,采用最优拉丁超立方抽样进行实验设计,利用BP神经网络构建准确的预测模型,再通过遗传算法极值寻优获得了最优的工艺参数组合。通过对工艺参数进行优化设计,得到了无侧壁起皱缺陷的零件,为解决铝板悬空区侧壁起皱提供一种可行的方法。
1 数值模拟 1.1 几何模型以铝合金圆锥形件为研究对象,对悬空区侧壁起皱行为进行研究。本文样件使用的材质为AA5042铝合金,料片尺寸为厚度0.208 3 mm,直径64.77 mm。
零件成形工序为倒装的单动拉延,模具几何模型及相关尺寸参数如图 1所示。该几何模型工具体由凸模、凹模、压边圈和板料组成,其中凸模、凹模和压边圈定义为刚体,板料定义为弹性体。凸凹模间隙为0.51 mm,凸模冲压行程为18 mm,工具体最大网格长度为1 mm。凸模中间部分设计为空心的作用主要是排气作用以及可达到减轻重量和节省造价等目的。
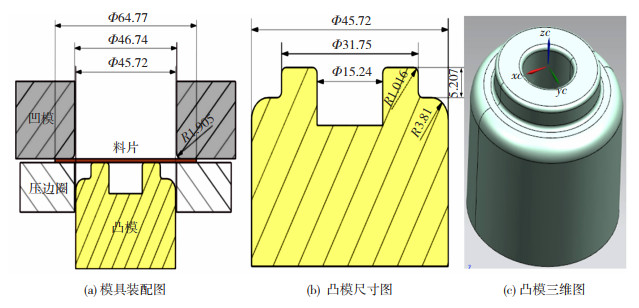
|
图 1 模具几何模型(单位:mm) Fig.1 Die geometric model: (a) die assembly drawing; (b) punch dimension drawing; (c) three-dimensional graph of convex module |
该圆锥形件材料物性参数如表 1所示。由表 1可知,铝合金薄板在与轧制方向成不同角度时塑性应变比差异较大,具有明显的各向异性行为。板材的平均塑性应变比R用3个方向塑性应变比的平均值表示,如公式(1)所示。R值越小,板材抵抗变薄的能力越差,越容易产生起皱、开裂等质量缺陷。平面各向异性参数▽R由公式(2)表示,数值越大代表板材平面内的各向异性越严重,越容易产生制耳现象和导致侧壁厚度不均匀。
| 表 1 铝合金AA5042物性参数 Table 1 physical parameters of aluminum alloy AA5042 |
| $ R=\left(R_0+2 R_{45}+R_{90}\right) / 4 $ | (1) |
| $ \nabla R=\left(R_0-2 R_{45}+R_{90}\right) / 2 $ | (2) |
式中:R0为与轧制方向呈0°时塑性应变比;R45为与轧制方向呈45°时塑性应变比;R90为与轧制方向呈90°时塑性应变比。
结合表 1和公式(1)可得铝合金薄板的平均塑性应变比为0.94,说明板材厚向变形较小,开裂风险较低。结合表 1和公式(2)可得铝合金薄板的平面各向异性参数为-0.194,其值为负,说明制耳波峰发生在与轧制方向为45°时。
依据表 2和表 3单、双轴拉伸实验数据进行比较分析,同时利用流变应力模型数据(该流变应力模型通过Voce公式拟合得到,如公式(3)所示),综合以上数据得到AA5042铝合金薄板单轴(与轧制方向呈0°、45°、90°)和双轴拉伸的真实应力- 真实塑性应变曲线如图 2所示。其中,AA5042铝板的屈服强度为277.17 MPa,抗拉强度为322.0MPa,加工硬化指数为0.096,屈强比为0.86。其加工硬化指数和屈强比较低,表明成形性能较差,在冲压成形过程中容易产生质量缺陷。
| 表 2 单轴拉伸实验数据 Table 2 Uniaxial tension test data |
| 表 3 双轴拉伸实验数据 Table 3 Equal biaxial tension test data |
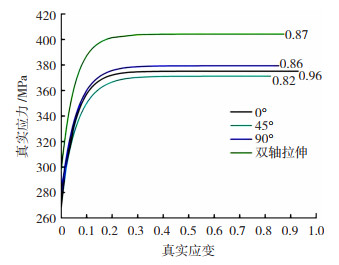
|
图 2 铝合金AA5042的真实应力- 真实塑性应变曲线 Fig.2 True stress-true plastic strain curves of aluminum alloy AA5042 |
文中的真实应力模型通过公式(3)(Voce公式)拟合得到,图 2横坐标是真实塑性应变(真实塑性应变=真实应变- 真实弹性应变),从纵坐标可以看出应力初始位置是从屈服应力开始的,所以图 2中看到的应力应变曲线是加工硬化的表现。
| $ \sigma=A-B \times \exp \left(-C \times \varepsilon_{\mathrm{p}}\right) $ | (3) |
式中:σ为流变应力;εp为真实塑性应变;A、B、C为拟合参数。冲压有限元软件Autoform中的硬化曲线一般为与轧制方向成0°的真实应力应变曲线,其拟合参数A、B、C分别为375.08,107.28和17.859 MPa。
正确地运用各向异性屈服准则能够有效提高数值模拟精度,因此本文选择先进的BBC屈服准则来描述铝板的各向异性行为。在Autoform有限元软件中定义BBC屈服准则至少需要7个参数,分别为3个方向的塑性应变比R0、R45、R90,3个方向的屈服强度σ0、σ45、σ90和屈服函数指数M。其中,3个方向的塑性应变比由表 2可得,3个方向的屈服强度分别为277.17、281.31和289.58 MPa,铝板的屈服函数指数M默认为8。
1.3 起皱标准铝合金圆锥形件在拉深成形过程中,侧壁区域处于悬空状态,不与模具发生直接接触,极易产生起皱失稳现象。铝合金薄板侧壁起皱程度由多种因素共同影响,如板料几何形状和尺寸、料厚比、材料性能参数、压边力、凸凹模圆角和润滑条件等。为了便于测量起皱的大小,本文采用起皱径向位移r和起皱幅值▽r来表征起皱程度,如图 3所示。其中,起皱径向位移r定义为以圆锥形件底部圆心为坐标系原点,建立如图 3(a)所示坐标系,轮廓上起皱最大值某点与原点之间距离为r。
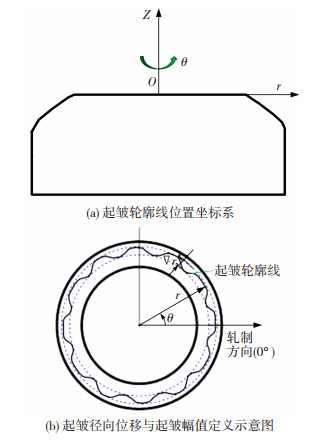
|
图 3 起皱评判标准 Fig.3 Evaluation criteria of wrinkle: (a) coordinate system for position of wrinkle curves; (b) defination diagram of wrinkling radial diaplacement and wrinkling amplitude |
拉深时在不同高度平面(如Z= -3.5 mm、Z= -4.5 mm、Z= -5.5 mm等)的不同角度的r值,以及设备的力位移曲线不同,实验中取Z= -4.5 mm时进行分析,该处板材剖面的起皱轮廓线到坐标中心的径向位移,起皱幅值▽r表示为最大起皱径向位移与最小起皱径向位移之差。
1.4 网格划分在Autoform冲压有限元软件中采用自适应网格技术对板料进行网格划分,物理量变化剧烈的区域采用精密网格,物理量变化平缓的区域采用粗大网格,在保证计算精度的同时提高计算效率。圆锥形件侧壁起皱行为对网格质量有较强的敏感性,采用不同网格参数模拟得到的仿真结果具有较大差异,其皱纹个数、起皱径向位移和起皱幅值与实验数值差异明显,因此选择合适的网格参数可以有效提高数值模拟精度[9]。
在冲压成形仿真模拟中,网格类型按对象不同可分为板料网格和工具体网格,其中板料网格参数对侧壁起皱行为影响较大。本文中采用的板料网格参数为:最大初始网格尺寸为4 mm,最大细化等级为6级,初始网格数量为1 900个,单元类型为弹塑性壳单元。
1.5 有限元模型的验证本文以圆锥形件为研究对象,在室温下进行拉深成形,根据零件特性以及冲压工艺要求,当两摩擦表面在载荷的作用下,由于边界膜较薄和金属表面凹凸不平,使得接触微凸体的压力很大,当两表面相互滑动时,接触点上的温度很高,使这部分的边界膜破裂,产生金属直接接触,因此有限元模型中的摩擦类型采用边界摩擦。
实验中板料成形数值模拟的结果是否接近于生产实际,接触摩擦的处理至关重要;板料成形过程中影响摩擦的因素众多,其因素主要包括: 接触压力、成形速度、板料及模具的材料、表面粗糙度、润滑剂以及即时变形情况等[10-11]。
当模具与板料两表面之间被极薄的润滑膜隔开,且润滑膜不遵从流体动力学定律及两表面之间的摩擦主要决定于两表面的特性和润滑剂的特性时,此时模具与板料之间就处于边界润滑状态[12],根据模具与板料接触状态的不同,对不同润滑条件下不同区域的摩擦模型进行了分析推导,建立了流体润滑等条件下的摩擦模型。
在冲压过程中使用的工艺参数如下:压边力为恒定值8.9 kN,摩擦系数为0.03,冲压速度为140 mm/s,下压距离为工件完全成型,约20 mm;冲压设备参数如表 4所示。根据冲压工艺以及品质要求,采用FABLE/福邦- 铝冲压油PO系列,其具有优良的润滑冷却性,冲压油能防止冲模与工件的粘结,提高表面质量,延长模具寿命,防止铝及其铝合金氧化,降低废品,且表面残留的油非常少,可减少清洗环节的成本,让工件表面更干净,提高工效。铝合金圆锥形件在经过拉深成形之后,侧壁悬空区发生严重起皱,仿真结果和实验结果对比如图 4所示。在实验结果中,圆锥形件的侧壁皱纹个数为13个;而在仿真结果中,侧壁皱纹个数为12个。一方面是由于有限元模型的对称性,皱纹个数只能为偶数;另一方面是由于实验过程中很难保证润滑条件均匀分布以及凸凹模和板料之间的对中性完全一致,铝材AA5042分析的起皱效果与实际冲压出来的外观基本一致,如图 4所示。铝材的各向异性差异较大,导致成型各个方向材料流动不一。
| 表 4 冲压设备参数 Table 4 Stamping equipment parameters |

|
图 4 成形结果 Fig.4 Forming result: (a)test result; (b)simulation result |
实验中为了直观地描述仿真模型的准确性,起皱轮廓线径向位移的仿真与实验结果对比如图 5所示。在实验结果中,起皱轮廓线的最大径向位移为22.21 mm,最小径向位移为19.78 mm,最大起皱幅值为2.43 mm;而在仿真结果中,起皱轮廓线的最大径向位移为21.88 mm,最小径向位移为19.63 mm,最大起皱幅值为2.25 mm,最大起皱幅值实验和仿真的相对误差为7.4%。圆锥形件的侧壁起皱轮廓线仿真值与实验值走势基本吻合,其中起皱轮廓线仿真值的平均径向位移为20.87 mm,起皱轮廓线实验值的平均径向位移为21.19 mm,相对误差仅为1.48%,因此该有限元模型是正确的,可用于指导成形工艺参数优化设计。
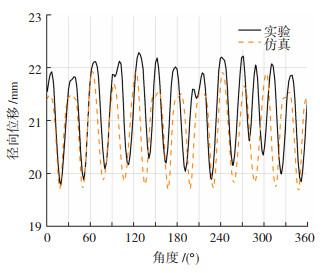
|
图 5 起皱轮廓线 Fig.5 Wrinkle curves |
肖良红、冯斌[13-14]提出的拉丁超立方抽样属于多维空间中的分层抽样,在一维空间中具有较好的均匀性,但在多维空间中由于各维参数随机组合,容易导致空间中某一区域样本点过于集中或稀疏,从而使样本失去对部分空间的代表性。因此,为了使样本点尽可能地“充满”整个空间,本文利用遗传算法对拉丁超立方抽样进行优化设计,以获得更加均匀的样本点分布。
本文将多维空间看作一个系统,该系统由一群样本粒子构成。各样本粒子相互存在排斥力,促使粒子在系统中不断运动,直至系统平衡。此时系统势能最低,样本粒子“充满”整个实验空间。其中,系统势能与粒子间距离的平方成反比,如式(4)所示
| $ E=\sum\limits_{i=1}^{N-1} \sum\limits_{j=i+1}^N \frac{1}{\left\|x_i-x_j\right\|^2} $ | (4) |
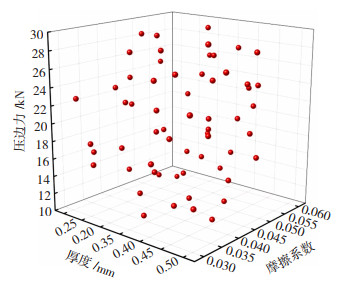
式中:E为系统势能;N为样本粒子数;xi和xj为第i和第j个样本粒子坐标;║xi-xj║为第i和第j个样本粒子之间的欧氏距离。以系统势能为适应度函数,利用遗传算法使系统势能取得最小值,此时系统处于平衡状态。通过优化后的拉丁超立方抽样获取的60个样本点在实验空间中的分布如图 6所示。
|
图 6 实验点分布 Fig.6 Distribution of test points |
本文以料厚、摩擦系数、压边力和冲压速度等4个参数为优化变量,以最大起皱幅值最小化为优化目标[15],各优化变量取值范围如表 5所示。根据最优拉丁超立方抽样获取的样本点,利用Autoform软件对铝合金薄板进行侧壁起皱分析,得到不同成形参数下的起皱幅值。由于该样本数据有60组,数据量过大,在此列出部分样本数据,具体如表 6所示。各实验样本的最大减薄率都小于12%,远低于冲压件30%的最大减薄率评判标准,因此该模型只考虑起皱缺陷对成形质量的影响。
| 表 5 优化变量及取值范围 Table 5 Optimization variables and value range |
| 表 6 部分样本数据及结果 Table 6 Partial sample datas and results |
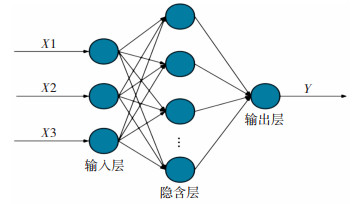
根据上述的样本数据及仿真结果,选用BP神经网络进一步预测圆锥形件侧壁起皱幅值。其中BP神经网络包含输入层、隐含层和输出层三部分结构,具有较强的非线性映射和泛化能力,适用于构建非线性预测模型,本文构建的神经网络结构如图 7所示。首先,将60个样本随机划分为训练集和测试集,训练集包含50个样本,测试集包含10个样本;其次,对实验数据归一化到区间[-1, 1],消除不同变量之间的量纲影响。然后初始化神经网络参数,李雷等[16]提出将起皱、厚度不均匀性、回弹量作为优化指标,利用人工神经网络代表优化变量与优化指标之间的关系,采用NSGA-II多目标遗传算法优化人工神经网络,获得帕累托前沿解集。
|
图 7 神经网络结构图 Fig.7 Structure of BP neutral network |
BP神经网络的隐含层层数、隐含层神经元数量和学习率对神经网络预测模型的预测精度具有很大的影响。本文是三输入,单一输出的神经网络模型,非线性映射关系相对简单,更适用于选用单隐含层网络结构。隐含层神经元数量范围一般由经验公式确定
| $ l<\sqrt{(m+n)}+a $ | (5) |
式中:l为隐含层神经元数量;m为输入层节点数;n为输出层节点数;a为0~10的常数。
根据公式(5)可得,该神经网络模型的隐含层神经元数量在[3, 13]之间。神经网络的学习率一般不宜过大,通常在0.1左右,取其范围在[0.01,0.2]之间。为了寻找最优的隐含层神经元数量和学习率,本文以测试集平均相对误差最小化作为优化目标,经过循环迭代之后得到的平均相对误差最小值为2.69%,对应的最优隐含层神经元数量为5,学习率为0.1。
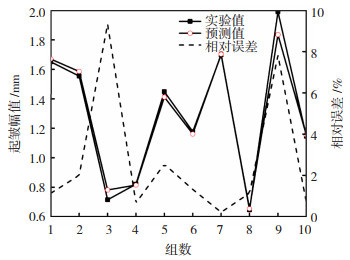
3.2 神经网络预测结果在MATLAB中编写神经网络代码,利用拉丁超立方实验数据及结果训练神经网络,并选择最优的隐含层神经元数量和学习率,提高了模型的预测精度,其训练结果如图 8所示。测试集平均相对误差为2.69%,最大相对误差为9.33%,最小相对误差为0.22%,拟合优度R2为0.9831,其表达式如式(6)所示。训练结果表明该神经网络模型具有极高的预测精度,在整个样本空间中的泛化能力较强,能够很好地应用于预测圆锥形件侧壁起皱幅值。
|
图 8 神经网络训练结果 Fig.8 Neural network training results |
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2}{\sum\limits_{i=1}^n\left(y_i-\bar{y}\right)^2} $ | (6) |
式中:R2为拟合优度;yi为实验值;
同理,可采用BP神经网络模型以及分析结果,进行分析、预测圆锥形件侧壁低减薄率的变化值,从而实现低减薄率的高质量目标零件。
4 遗传算法寻优及验证 4.1 遗传算法寻优优化铝合金圆锥形件在成形过程中侧壁起皱幅值F(X)的数学模型和约束条件如式(7)所示。
| $ \begin{aligned} & F(X)=\min f\left(x_1, x_2, x_3\right) \\ & \text { s.t. }\left\{\begin{array}{l} 0.2 \mathrm{~mm} \leqslant x_1 \leqslant 0.5 \mathrm{~mm} \\ 0.03 \leqslant x_2 \leqslant 0.06 \\ 10 \mathrm{kN} \leqslant x_3 \leqslant 30 \mathrm{kN} \\ 140 \mathrm{~mm} / \mathrm{s} \leqslant x_4 \leqslant 800 \mathrm{~mm} / \mathrm{s} \end{array}\right. \\ & \end{aligned} $ | (7) |
式中:x1为料厚;x2为摩擦系数;x3为压边力;f(x1,x2,x3)为最大起皱幅值。
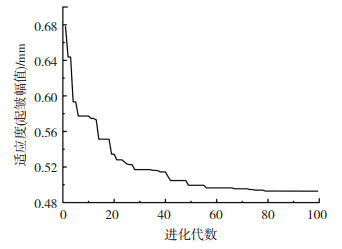
基于以上算法基础将训练好的神经网络预测模型作为遗传算法的适应度函数,最大进化代数为100,种群规模为20,交叉概率为0.4,变异概率为0.2。经过选择、交叉和变异等程序,求解待优化函数模型的全局最优解,遗传算法迭代寻优的适应度曲线如图 9所示。寻优结果表明,经过100次迭代之后,适应度(起皱幅值)收敛于0.492 9 mm,相关最优成形参数如表 7所示。
|
图 9 适应度曲线 Fig.9 Fitness curve |
| 表 7 最优成形参数 Table 7 Optimal forming parameters |
将遗传算法求得的最优成形参数代入冲压有限元软件Autoform仿真验证,导出起皱轮廓线之后,在UG软件中测量得到优化后的侧壁起皱幅值为0.513 6 mm,与遗传算法寻优预测的起皱幅值0.492 9 mm相比较,可得两者的相对误差为4.03%。
为了更好地描述优化后的成形参数对成形质量的改善效果,以软件自带的起皱准则作为依据,其起皱准则如式(8)所示。
| $ \text { wrinkles }=\frac{t}{2 R} $ | (8) |
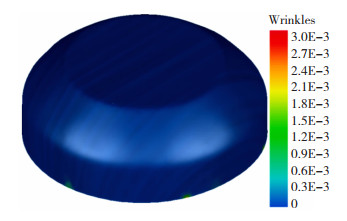
式中:wrinkels为起皱值,属于无量纲数值;t为板料厚度;R为曲率半径。起皱值云图如图 10所示,一般起皱值不得超过0.1。
|
图 10 起皱云图 Fig.10 Wrinkles cloud chart |
由图 10可见,经过极值寻优成形出的圆锥形工件,其最大起皱值不超过0.003,侧壁起皱值全为0,说明零件不存在起皱缺陷,证明了该方法的有效性。通过最优成形参数求得的最大起皱幅值比原实验最大起皱幅值2.43 mm下降了78.9%,表明利用神经网络和遗传算法极值寻优可以有效地解决铝合金侧壁起皱缺陷。
5 结论1) 以铝合金圆锥形件为研究对象,通过建立材料模型和选择合适的网格参数,分析了铝合金侧壁起皱轮廓线与基于优化后的参数,并进行实验验证,结果基本一致,验证了有限元模型的准确性和可靠性。
2) 利用遗传算法优化拉丁超立方抽样,获取了更加均匀的试样点分布。通过训练样本建立了BP神经网络预测模型,测试集平均相对误差为2.69%,最大相对误差为9.33%,最小相对误差为0.22%,拟合优度R2为0.9831,表明该神经网络模型具有极高的预测精度。
3) 以最大起皱幅值最小化为优化目标,通过遗传算法极值寻优获得了最优的成形参数,即料厚0.486 mm,摩擦系数0.0552,压边力28.9 kN和冲压速度278.10 mm/s,代入Autoform软件中进行数值模拟验证,最大起皱幅值的预测值和有限元值分别为0.492 9和0.513 6 mm,相对误差仅为4.03%,表明利用神经网络和遗传算法极值寻优可以有效解决铝合金侧壁起皱缺陷。
| [1] |
DICK R E, YOON J W. Wrinkling during cup drawing with NUMISHEET2014 benchmark test[J]. Steel Research International, 2015, 86(8): 915-921. DOI:10.1002/srin.201500018 |
| [2] |
NETO D M, OLIVEIRA M C, DICK R E, et al. Numerical and experimental analysis of wrinkling during the cup drawing of an AA5042 aluminium alloy[J]. International Journal of Material Forming, 2017, 10(1): 125-138. DOI:10.1007/s12289-015-1265-4 |
| [3] |
OIDE K, MIHARA Y, KOBAYASHI T, et al. Drawing simulation by static implicit analysis with the artificial damping method[J]. Journal of Physics: Conference Series, 2016, 734(3): 032039. DOI:10.1088/1742-6596/734/3/032039 |
| [4] |
高亚南, 李彦波, 曹大兴, 等. 基于绕弯成形工艺的铝型材截面优化研究[J]. 材料科学与工艺, 2021, 29(4): 81-86. GAO Yanan, LI Yanbo, CAO Daxing, et al. Research on section optimization of aluminum profiles based on rotary-draw bending process[J]. Materials Science and Technology, 2021, 29(4): 81-86. DOI:10.11951/j.issn.1005-0299.20200209 |
| [5] |
朱英霞, 万苗苗, 陈炜, 等. 铜钛双金属复合管绕弯成形回弹的尺寸效应研究[J]. 材料科学与工艺, 2021, 29(6): 10-17. ZHU Yingxia, WAN Miaomiao, CHEN Wei, et al. Size effect of springback on rotary-draw bending of copper-titanium composite tube[J]. Materials Science and Technology, 2021, 29(6): 10-17. DOI:10.11951/j.issn.1005-0299.20210203 |
| [6] |
TANONGSAK B, SUTHEP Y, SANSOT P. Wrinkling prediction of rectangular cup deep drawing process for aluminum alloy sheets by using the modified yoshida buckling test[J]. Key Engineering Materials, 2020, 6036: 143-151. DOI:10.4028/www.scientific.net/KEM.856.143 |
| [7] |
SUN Zhiying, LANG Lihui, LI Kui, et al. Study on the mechanism and the suppression method of wrinkling in side wall using hydroforming of the fairing[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(9-12): 2527-2535. DOI:10.1007/s00170-016-9606-0 |
| [8] |
李振杰. 半球形冲压件起皱因素的分析[J]. 锻压技术, 2014, 39(5): 56-60, 95. LI Zhenjie. Analysis of wrinkling factors for hemispherical stamping parts[J]. Forging & Stamping Technology, 2014, 39(5): 56-60, 95. DOI:10.13330/j.issn.1000-3940.2014.05.012 |
| [9] |
李晶. 汽车侧围前连接板冲压成形质量优化研究[J]. 材料科学与工艺, 2023, 31(2): 90-96. LI Jing. Optimization forstamping formingquality of front connecting plate of automobile side panel[J]. The International Journal of Advanced Manufacturing Technology, 2023, 31(2): 90-96. DOI:10.11951/j.issn.1005-0299.20220107 |
| [10] |
何泽歆, 黄超群. 基于克里金模型和智能算法的汽车加强件热冲压工艺优化[J]. 锻压技术, 2020, 45(10): 47-52. HE Zexin, HUANG Chaoqun. Optimization of hot stamping process for automobile reinforcement part based on Kriging model and intelligent algorithm[J]. Forging&Stamping Technology, 2020, 45(10): 47-52. DOI:10.13330/j.issn.1000-3940.2020.10.008 |
| [11] |
LEE B H, KEUM Y T, WAGONER R H. Modeling of the friction caused by lubrication and surface roughness in sheet metal forming[J]. Journal of Mterials Processing Teehnology, 2002, 130: 60-63. DOI:10.1016/S0924-0136(02)00784-7 |
| [12] |
戴雄杰. 摩擦学原理[M]. 上海: 上海科学技术出版社, 1984. DAI Xiongjie. Tribological principle[M]. Shanghai: Shanghai Science and Technology Press, 1984. |
| [13] |
肖良红, 罗慧娜, 向俊仲, 等. 基于AutoForm的轿车行李箱内板成形工艺优化[J]. 锻压技术, 2014, 39(6): 60-64. XIAO Lianghong, LUO Huina, XIANG Junzhong, et al. Forming process optimization for inner panel of car trunk lid based on AutoForm[J]. Forging&Stamping Technology, 2014, 39(6): 60-64. DOI:10.13330/j.issn.1000-3940.2014.06.012 |
| [14] |
冯斌, 毛建中, 胡晖. 基于BP神经网络的条带刚凸特征回弹预测[J]. 锻压技术, 2020, 45(3): 20-26. FENG Bin, MAO Jianzhong, HU Hui. Springback prediction on rigidity and convexity charateristices ofstrip based on BP neural network[J]. Forging&Stamping Technology, 2020, 45(3): 20-26. DOI:10.13330/j.issn.1000-3940.2020.03.004 |
| [15] |
王泌宝. 汽车B柱加强板热冲压工艺的遗传算法多目标优化[J]. 锻压技术, 2021, 46(5): 46-52. WANG Mibao. Multi-objective optimization on hot stamping process for vehicle B-pillar reinforced plate based on genetic algorithm[J]. Forging&Stamping Technology, 2021, 46(5): 46-52. DOI:10.13330/j.issn.1000-3940.2021.05.008 |
| [16] |
李雷, 赵柏森. 基于人工神经网络和遗传算法的封头成形工艺参数多目标优化[J]. 锻压技术, 2021, 46(5): 39-45. LI Lei, ZHAO Baisen. Multi-objective optimization on head forming process parameters based onartificial neural network and genetic algorithm[J]. Forging&Stamping Technology, 2021, 46(5): 39-45. DOI:10.13330/j.issn.1000-3940.2021.05.007 |
 2024, Vol. 32
2024, Vol. 32


