2. 潍坊职业学院 汽车工程学院,山东 潍坊 262737;
3. 南京理工大学 机械工程学院,南京 210094;
4. 皖江工学院 机械工程学院,安徽 马鞍山 243031
2. School of Automotive Engineering, Weifang Vocational College, Weifang 262737, China;
3. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;
4. School of Mechanical Engineering, Wanjiang University of Technology, Ma'anshan 243031, China
作为一种传统的吸能结构,金属薄壁管具有轻量化、高比刚度、高比强度与高吸能效率等优点[1],被广泛应用于航空航天、汽车、轨道交通等工程领域[2-4]。金属薄壁管在服役过程中往往承受着轴向压缩及弯曲压力,在变形吸能过程中变形模式不稳定,其屈曲失稳问题限制了吸能特性的发挥,因此金属薄壁管轴向压缩性能的研究与优化一直是结构抗冲击吸能领域的研究重点[5]。目前,围绕金属薄壁管力学性能与吸能效率提高的研究主要集中在增加填充物前后的实验对比研究[6]、工艺理论研究[7-8]以及仿真与实验对比研究[9]。其中,泡沫铝等一类多孔材料由于其良好的轻质吸能特性,被应用于薄壁管填充设计,对提高其抗压缩性能有着重要的现实意义。另外,相关研究人员所设计的一些特别的填充薄壁复合结构在具备轻量化的同时,还达到了良好的吸能和抗冲击性能方面的综合收益[9-10]。
负泊松比超材料(Negative Poisson's Ratio, NPR)是一种典型的机械超材料,受压时材料向内部聚集,瞬时密度增大,伴随着独特的收缩变形现象,呈现出负泊松比、多孔轻质、高比强度和抗冲击等超常规力学性能[11-12],是目前国际上公认的最有前景的新型超强韧轻质材料结构之一[13-15]。Gibson等[16]在普通蜂窝的基础上首次提出了泊松比为-1的内凹六边形蜂窝,并且推导了结构弹性参数的解析式。Lakes[17]基于可旋转圆形节点的手形结构的概念首次提出了六韧带手性蜂窝结构的力学超材料。Gao等[18]创新性地提出了一种碳纤维增强复合材料负泊松比点阵结构及其制备方法,并结合理论模型系统研究了准静态压缩特性。Joseph等[19]对比了不同构型的负泊松比蜂窝材料的等效力学性能,认为双箭头几何构型结构的等效弹性模量和屈服强度相对较高,其静力承载性能也优于其他类型负泊松比超材料。刘璐[20]提出了一种随机负泊松比泡沫填充薄壁结构,并利用有限元方法对其进行力学特性分析,研究其在轴向冲击载荷作用下的屈曲模态和能量吸收性能。鲍呈浩等[21]通过实验和数值模拟相结合的方法研究了周期性点阵填充双薄壁管吸能结构在轴向压载条件下的能量吸收能力,结果表明其比能量吸收、碰撞力效率等抗撞性能有良好提升。Liu等[22]分析了有无负泊松比泡沫填充物的薄壁圆管结构的轴向冲击吸能特性,结果表明填充管具有较大的吸能量和较高的比吸能率,在此基础上,设计了不同层数的多层负泊松比泡沫填充管。Mohsenizadeh等[23-24]采用数值模拟的方法对比研究了具有不同泊松比值(-0.31~-0.03) 的负泊松比泡沫填充方管的轴向压缩吸能特性,结果表明随着负泊松比泡沫泊松比值的提高(效应减弱),填充管比吸能率的提高量逐渐下降直至区域稳定,但仍高于空心方管。
综上可知,目前针对负泊松比薄壁填充结构的研究主要集中在负泊松比泡沫作为填充物的薄壁结构设计,但负泊松比泡沫自身绝对抗压刚度和强度较低,无法满足更高的冲击吸能需求,而目前针对负泊松比金属点阵填充薄壁结构在压缩载荷下力学性能的研究还不充分。因此,为了进一步提高薄壁管的力学性能,提出了一种结合双箭头型负泊松比点阵结构与金属薄壁管的新型填充式薄壁吸能结构,采用经典方法对相互作用效应进行解耦,建立了其力学性能表征模型,并结合轴向压缩实验与数值仿真分析的方法验证了理论模型的可靠性。在此基础上,研究了填充式薄壁吸能结构的变形失效模式与力学响应,并进一步分析了结构设计参数对力学性能的影响规律。
1 实验设计与有限元模拟 1.1 填充管结构设计本文将双箭头型负泊松比点阵结构填充于方形截面金属薄壁管内部,从而形成一种新型填充式薄壁吸能结构,如图 1所示。本文采用的双箭头构型负泊松比结构是在Gibson[16]提出的二维内凹六边形蜂窝结构的基础上演化而来,目前已有部分研究报道了该结构诸多优异力学性能[25-26],其三维点阵结构是由双箭头型胞元结构在三维方向阵列而成,每个胞元结构是由8根正方形截面杆件构成,分为上肋杆和下支撑杆,图中结构参数可表示为:胞元的半宽为d,上肋杆和下支撑杆与垂直方向夹角分别是θ2、θ1,以及胞元杆件壁厚为b。方形截面金属薄壁管的结构参数为:薄壁管高度为h,薄壁管截面宽度为w,薄壁管壁厚为t。

|
图 1 新型填充管结构示意图 Fig.1 Structure diagram of new type filling pipe |
结构的相对密度与薄壁管耐撞性能直接相关,因此进一步分析结构设计参数对相对密度的影响,该填充管相对密度可通过结构实际体积与所占空间体积之比表示
| $ \rho_{\mathrm{R}}=\frac{V_{\text {tule }}+V_{\mathrm{NPR}}}{V^{\prime}} $ | (1) |
式中Vtube、VNPR、V′分别是薄壁管、负泊松比点阵和填充管的体积。他们可分别表示为:
| $ V_{\text {tube }}=w^2 h-(w-2 t)^2 h $ | (2) |
| $ V_{\mathrm{NPR}}=2 b^2\left(\frac{d}{\sin \theta_1}+\frac{d}{\sin \theta_2}\right) n_x n_y n_z $ | (3) |
| $ V^{\prime}=w^2 h $ | (4) |
式中nx、ny、nz分别是双箭头型负泊松比点阵结构在各个正交方向上的胞元个数,且nx=ny。同时,由于点阵结构是紧密填充于薄壁管内部,因此薄壁管的尺寸可表示为:
| $ w=2 d n_x+2 t $ | (5) |
| $ h=\left(\frac{d}{\tan \theta_1}-\frac{d}{\tan \theta_2}\right) n_z $ | (6) |
将式(1)~(6)相结合,即可通过所述结构参数(t、d、b、θ1、θ2、nx、nz)确定填充管的细观构型及相对密度。
1.2 轴向准静态压缩实验进一步通过准静态压缩实验与数值仿真分析的方式研究填充管的轴向压缩性能,并进一步对比分析压缩过程中的载荷特性,以验证上述理论模型的可靠性。用于验证分析的填充管的结构参数设置如下:h=70 mm、w=40 mm、t=1 mm、d=5 mm、b=1 mm、θ1=30°、θ2=60°、nx=2、nz=6。基体材料采用合金钢,其材料参数为:弹性模量E=215 GPa,泊松比μ=0.25,屈服强度ReL= 229 MPa。采用激光选择性熔化技术(SLM)制备的样件如图 2(a)所示。参考GB/T 1453—2005的要求,在INSTRON 3360 (10 kN)万能试验系统上采用位移加载的形式进行压缩实验,压缩速度为2 mm/min,压缩总位移为60 mm,实验装置如图 2(b)。样件放置在上下两个刚性压头之间,通过上压头内置的力传感器,可直接测量压缩载荷-位移数据。

|
图 2 填充管轴向准静态压缩实验 Fig.2 Axial quasi-static compression experiment of filled tube: (a) prototype; (b) experimental device |
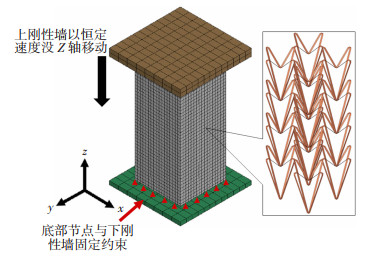
基于HYPERWORKS有限元软件对填充管轴向压缩性能进行有限元仿真分析,仿真模型的结构参数、材料属性与实验样件保持一致,建立的有限元仿真模型如图 3所示,薄壁管和点阵填充结构均采用CQUAD4壳单元(shell 63)进行网格划分,通过网格灵敏度验证后,仿真模型网格基本尺寸确定为0.5 mm。建立与填充管居中对齐的上下刚性墙,分别模拟压缩实验中的顶部压头与底部承载,顶部刚性墙采用强制位移加载的方式以2 mm/min的恒定速度沿Z轴逐渐移动压缩填充管,填充管底部节点与下刚性墙采用固定端约束。为保证计算收敛性,刚性墙与填充管、薄壁管与填充结构之间采用面-面自动接触(Type1),结构自身为避免穿透采用单面自接触(Type7)。
|
图 3 轴向准静态压缩有限元模型 Fig.3 Finite element model of axial quasi-static compression |
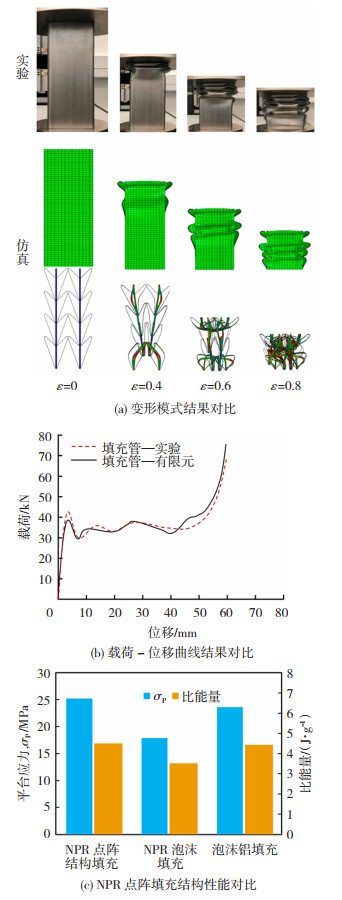
基于上述实验与有限元仿真,得到了填充管在轴向准静态压缩载荷下的变形模式和载荷-位移曲线,如图 4所示。从4(a)可知,准静态压缩实验中填充管的变形失效模式与有限元结果基本一致,均是从中间段出现坍塌形成标准褶皱,而后逐渐溃缩变形。图 4(b)描绘了填充管在压缩过程中的载荷位移曲线,从图中对比可知实验与有限元结果吻合良好,这表明建立的有限元模型能准确地模拟填充管的轴向压缩力学响应。从图 4(b)中可以看出,填充管压缩载荷曲线呈现明显的三段式特征:第一阶段为弹性阶段,载荷随着压缩位移逐渐增加,并逐渐到达初始峰值;第二阶段为载荷振荡平台阶段,在这个阶段填充管开始产生屈服变形,溃缩褶皱逐层产生,载荷随位移逐渐振荡,形成一个稳定的平台期;第三阶段为密实化阶段,填充管的外部薄壁管与内部填充结构均达到密实化应变,载荷迅速上升。通过对比载荷曲线中的特征值可知,实验中获得的初始峰值为41.5 kN、平均碰撞力为31.6 kN;仿真获得的初始峰值为39.6 kN、平均碰撞力为30.2 kN,误差均在5%以内,说明有限元仿真结果是可靠的。
|
图 4 填充管轴向准静态压缩性能 Fig.4 The axial quasi-static compression properties of the auxetic lattice filled tubes: (a) deformation mode validation; (b) load-displacement curve validation; (c) compression properties comparison |
为了进一步研究负泊松比点阵填充结构的性能,将本文提出结构与典型泡沫铝填充管[27]及负泊松比泡沫填充管[22]的轴向压缩性能进行对比(平台应力σP和比能量(SEA,比能量取压缩行程终了时的值)),结果如图 4(c)所示,从图中可知,NPR点阵填充管的压缩平台应力和比吸能显著优于NPR泡沫填充管,这主要是因为泡沫填充内芯的压缩强度和刚度较低;NPR点阵填充管和泡沫铝填充管的压缩性能虽然相近,但典型泡沫铝存在孔隙率低、计算复杂、成本高等问题,较难实现填充管的准确参数化设计,而本文提出的NPR点阵填充管可以通过薄壁结构和点阵结构的参数优化,探求具有最佳吸能效果的填充管结构。
图 5为通过有限元仿真获得的不同结构应力应变以及能量吸收曲线,图中同时列出了单独针对薄壁管与点阵结构进行轴向准静态压缩有限元仿真获得的特性曲线。

|
图 5 不同结构抗压缩力学特性对比 Fig.5 Comparison of mechanical properties of different structures against compression: (a) stress-strain curve; (b) specific energy strain curve |
从图 5(a)可以看出,对于点阵填充管,在小变形下,应力基本呈现线性升高趋势,当压缩应变到达约0.015时应力达到峰值,应力曲线在轻微下降后进入平台阶段;薄壁方管的应力曲线会在到达峰值进入平台区间时出现快速下降的阶段;双箭头点阵填充结构的曲线变化趋势与填充管基本一致,但应力水平显著低于填充管。从曲线对比可知,填充管与薄壁方管相比具有更稳定的抗压缩力学特性。图 5(b)中进一步对比了不同结构在压缩过程中的比吸能曲线,其中新型填充管的吸能曲线比单独薄壁管与点阵结构在压缩过程中的叠加高约25%,这主要是因为填充管中薄壁管与填充结构之间的耦合变形效应。通过分析两者的变形可以看出强化效应主要是因为压缩过程中点阵结构杆件对管壁的支撑,同时在压溃区域轴向和周向载荷的共同作用下,填充管形成致密压缩,导致了碰撞力的整体增加,提高了填充管的吸能特性和能量吸收效率。
2.2 抗压缩性能参数分析由上述分析可知在填充管轴向压缩过程中负泊松比填充结构对薄壁管具有强化作用,需要进一步研究填充结构几何设计参数对抗压缩性能的影响。依次改变4个填充结构设计参数(d、b、θ1、θ2)的同时保持其余设计参数不变,通过仿真分别得到结构的平台应力σP和比能量(SEA)如图 6所示。从图 6中可知,不同结构设计参数对填充管吸能指标具有不同的影响规律。图 6(a)为胞元半宽d对填充管吸能指标的影响,随着d的逐渐增加,填充管的σP和SEA略有增加,但变化不明显,这表明胞元半宽对填充管准静态压缩性能影响较小。胞元半宽参数的变化并不影响胞元结构的细观构型,但与点阵填充结构的宏观尺寸相关,从图 6(a)的变化趋势可知,填充管准静态压缩性能的尺寸效应在所研究的参数范围内不显著。

|
图 6 填充管吸能指标与结构设计参数关系 Fig.6 Relationship between energy absorption index of filled tube and structural design parameters: (a) cell half width; (b) wall thickness of member; (c) included angle of lower support rod; (d) included angle of upper rib |
图 6(b)为胞元杆件壁厚b对填充管吸能指标的影响,填充管的σP和SEA会随着b的增加而增加,且变化趋势明显,表明胞元杆件壁厚对填充管准静态抗压缩性能影响较大,呈现正相关。从理论模型的建立过程中可知,胞元杆件壁厚越大,则杆件的截面惯性矩增大,杆件稳定性越高,抗屈曲失效性能提高,从而提高了点阵填充结构的抗压缩性能。
图 6(c)、(d)分别为下支撑杆夹角θ1、上肋杆夹角θ2对填充管吸能指标的影响,填充管的σP和SEA随θ1、θ2的增加而降低,其中θ1对结构抗压缩性能的影响略强于θ2。通过建立胞元结构在轴向压缩中的力学模型可知,下支撑杆主要承受轴向压缩与弯曲载荷,而上肋杆主要承受轴向拉伸与弯曲载荷。考虑到在结构压缩过程中塑性铰与杆件屈曲是主要失效形式,当θ1增加时,下支撑杆的抗屈曲性能下降,削弱了点阵填充结构的抗压缩性能;而θ2增加时,对于点阵填充结构的抗压缩性能的削弱并不显著。
3 平均碰撞力理论预测与分析为了进一步研究填充管的轴向压缩动态性能,本文基于Wierzbicki等[28]提出的泡沫铝填充管的平均碰撞力的理论预测模型,建立负泊松比点阵结构填充管的等效平均碰撞力Pm的理论公式
| $ P_{\mathrm{m}}=C_1 P_{\mathrm{t}}+C_2 P_{\mathrm{NPR}} $ | (7) |
式中:Pt、PNPR分别表示薄壁管与填充结构的平均碰撞力;C1、C2分别表示对应字结构的耦合强化系数,取C1 = C2 = 1.25。
薄壁管在折叠变形过程中通过形成塑性铰而吸收压缩能量,因此可以通过确定变形区域的薄膜耗散能的解析解,从而求解得到薄壁管的平均碰撞力。Wierzbicki等[28]提出方形薄壁管的塑性绞线包括水平固定绞线以及倾斜移动绞线。对于水平固定的塑性绞线,通过积分可求得其塑性耗散能W1
| $ W_1=2 \int_0^{\frac{\pi}{2}} M_0 w \mathrm{~d} \alpha=\pi M_0 w $ | (8) |
式中:α表示塑性铰弯曲角度,M0为薄壁管塑性极限弯矩,可表示为
| $ M_0=\sigma_y t \frac{2 w^2+(w-2 t)^2}{2} $ | (9) |
式中σy为填充管材料屈服应力。
对于有倾斜性的绞线的塑性耗散能W2可表示为
| $ W_2=4 M_0 I_2\left(\psi_0\right) h^2 / t $ | (10) |
式中I2(ψ0)表示薄壁管截面二次惯性矩且I2(ψ0)=1.11。
除上述两种耗散能以外,当材料发生强制折叠变形时,会在折痕处形成一个圆弧状曲面,在该区域内材料也会发生塑性变形而耗散能量,相应的耗散能W3可表示为
| $ W_3=16 M_0 \frac{h b}{t} I_3\left(\psi_0\right) $ | (11) |
式中I3(ψ0)表示薄壁管截面二次惯性矩且I3(ψ0)=0.58。
根据塑性能做功守恒定理,其平均碰撞力Pt为
| $ P_{\mathrm{t}}=\frac{W_1+W_2+W_3}{2 h} $ | (12) |
将式(8)、式(10)、式(11)分别带入式(12),根据能量最小原理
| $ P_{\mathrm{t}}=9.56 \sigma_y t^{\frac{5}{3}} w^{\frac{1}{3}} $ | (13) |
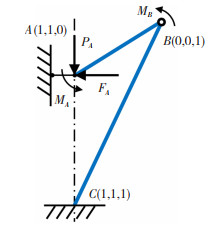
在轴向压缩过程中,双箭头型负泊松比点阵结构的坍塌失效行为主要包含塑性铰、胞壁屈曲以及弯曲失效。如图 7所示,建立胞元结构面内压缩受力示意图。根据图 7所示,A点在外力的作用下产生的位移为uZA
|
图 7 双箭头型负泊松比胞元结构压缩受力分析 Fig.7 Compressive force analysis of double arrow head cell structure with negative Poisson′s ratio |
| $ u_Z^A=d \frac{\sin \left(\theta_2-\theta_1\right)-\sin \theta_2+\sin \theta_1}{\sin \theta_1 \sin \theta_2} $ | (14) |
根据塑性耗散理论,绞线处的塑性耗散能等于外力所作的功
| $ (2 \mathrm{~d})^2 \sigma_0 u_Z^A=8 M_{\mathrm{P}} \theta_2 $ | (15) |
式中:MP为塑性弯矩;σ0为胞元结构等效失效应力,可表示为
| $ \sigma_0=\frac{2 M_{\mathrm{P}} \theta_2}{\mathrm{~d}^3} \frac{\sin \theta_1 \sin \theta_2}{\sin \left(\theta_2-\theta_1\right)-\sin \theta_2+\sin \theta_1} $ | (16) |
对于具有方形截面的理想弹塑性梁,塑性弯矩Mp可表达为
| $ M_{\mathrm{P}}=\frac{1}{4} b^3 \sigma_y $ | (17) |
将式(16)、(17)相结合,即可求得点阵结构面内压缩等效失效应力σ0
| $ \sigma_0=\frac{1}{2}\left(\frac{\mathrm{b}}{\mathrm{d}}\right)^3 \frac{\theta_2 \sin \theta_1 \sin \theta_2}{\sin \left(\theta_2-\theta_1\right)-\sin \theta_2+\sin \theta_1} \sigma_y $ | (18) |
进一步即可求得点阵结构平均碰撞力PNPR
| $ P_{\mathrm{NPR}}=\sigma_0\left(2 d n_x\right)^2 $ | (19) |
将求得的薄壁管平均碰撞力Pt(式(13))、点阵结构平均碰撞力PNPR(式(19))代入式(7),即可求得填充管平均碰撞力Pm的理论表达式
| $ \begin{aligned} P_{\mathrm{m}}= & 11.95 \sigma_{\mathrm{y}} t^{\frac{5}{3}} w^{\frac{1}{3}}+0.625\left(\frac{b}{d}\right)^3 \times \\ & \frac{\theta_2 \sin \theta_1 \sin \theta_2}{\sin \left(\theta_2-\theta_1\right)-\sin \theta_2+\sin \theta_1} \sigma_y\left(2 d n_x\right)^2 \end{aligned} $ | (20) |
表 1通过对具有不同结构设计参数的模型进行仿真分析来验证所建立的平均碰撞力理论公式的可靠性。从表 1中数据对比可知平均碰撞力的解析模型与仿真结果误差在8%以内,且理论值均低于仿真值,这主要是因为基于经典梁理论和能量守恒定律构建点阵结构等效失效应力时仅考虑了杆件的弯曲变形,忽略了杆件的剪切变形,从而导致理论结果略低于仿真获得的实际碰撞力,但总体来说解析模型预测精度是可以接受的,表明所建立的理论模型能准确的预测填充管的平均碰撞力。
| 表 1 结构设计参数变化表 Table 1 Table of structural design parameter changes |
本文将双箭头型负泊松比点阵结构与金属薄壁管相结合提出一种新型填充式薄壁吸能结构,并通过准静态压缩实验和有限元数值模拟方法研究了该结构在压缩载荷作用下的力学响应与吸能特性,具体结论如下。
1) 填充管在压缩载荷作用下的失效模式为局部屈曲失效,其压缩载荷-位移曲线呈现典型的三段式特征,压缩过程中薄壁管与填充结构的相互耦合也提高了填充管抗压缩性能。
2) 通过参数分析探明了点阵结构的细观设计参数对填充管吸能特性的影响,其中胞元杆件壁厚的增加会提高结构吸能特性,而胞元杆件夹角的增加则会降低结构吸能特性。
3) 基于Wierzbicki耦合理论建立了新型填充管的等效平均碰撞力预测模型,通过有限元数值仿真验证了理论模型的可靠性,为后续负泊松比点阵填充结构的抗冲击优化设计提供重要参考。
| [1] |
李光霁, 刘新玲. 汽车轻量化技术的研究现状综述[J]. 材料科学与工艺, 2020, 28(5): 47-61. LI Guangji, LIU Xinling. Literature review on research and development of automotive lightweight technology[J]. Materials Science and Technology, 2020, 28(5): 47-61. DOI:10.11951/j.issn.1005-0299.20190232 |
| [2] |
吴文旺, 肖登宝, 孟嘉旭, 等. 负泊松比结构力学设计、抗冲击性能及在车辆工程应用与展望[J]. 力学学报, 2021, 53(3): 611-638. WU Wenwang, XIAO Dengbao, MENG Jiaxu, et al. Mechanical design, impact energy absorption and applications of auxetic structures in automobile lightweight engineering[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(3): 611-638. DOI:10.6052/0459-1879-20-333 |
| [3] |
张向奎, 李昭, 韩成祥, 等. 热塑性玻璃纤维头盔服役性能分析与数值仿真[J]. 材料科学与工艺, 2023, 31(1): 1-9. ZHANG Xiangkui, LI Zhao, HAN Chengxiang, et al. Service performance analysis and numerical simulation of glass fiber thermoplastic helmets[J]. Materials Science and Technology, 2023, 31(1): 1-9. DOI:10.11951/j.issn.1005-0299.20220164 |
| [4] |
孙亚东, 周芸, 汪天尧, 等. 泡沫钢的制备及压缩吸能特性[J]. 材料科学与工艺, 2019, 27(5): 44-51. SUN Yadong, ZHOU Yun, WANG Tianyao, et al. Preparation process, compression and energy absorption properties of steel foams[J]. Materials Science and Technology, 2019, 27(5): 44-51. DOI:10.11951/j.issn.1005-0299.20180026 |
| [5] |
韦铁平, 周兴洋, 郭金泉, 等. A6061薄壁圆锥管轴向压缩性能的数值分析和理论研究[J]. 中国机械工程, 2022, 33(14): 1725-1733, 1750. WEI Tieping, ZHOU Xingyang, GUO Jinquan, et al. Numerical analysis and theoretical studies of axial compression behavior of A6061 thin-walled conical tubes[J]. China Mechanical Engineering, 2022, 33(14): 1725-1733, 1750. DOI:10.3969/j.issn.1004-132X.2022.14.011 |
| [6] |
NAJIBI A, GHAZIFARD P, ALIZADEH P. Numerical crashworthiness analysis of a novel functionally graded foam-filled tube[J]. Journal of Sandwich Structures and Materials, 2021, 23(5): 1635-1661. DOI:10.1177/1099636219900334 |
| [7] |
BARZIGAR S S, AHMADI H, LIAGHAT G H. An analytical investigation on the crushing behavior of thin-walled tubes filled with a foam with strain hardening region[J]. Thin-Walled Structures, 2023, 182: 110169. DOI:10.1016/j.tws.2022.110169 |
| [8] |
LIU H, CHNG Z X C, WANG G, et al. Crashworthiness improvements of multi-cell thin-walled tubes through lattice structure enhancements[J]. International Journal of Mechanical Sciences, 2021, 210: 106731. DOI:10.1016/j.ijmecsci.2021.106731 |
| [9] |
杨旭东, 许佳丽, 邹田春, 等. 泡沫铝填充金属薄壁管复合结构的研究进展[J]. 材料导报, 2019, 33(21): 3637-3643. YANG Xudong, XU Jiali, ZOU Tianchun, et al. Advances in the composite structure of aluminum foam filled metal thin-walled tube[J]. Materials Reports, 2019, 33(21): 3637-3643. DOI:10.11896/cldb.18080101 |
| [10] |
卢子兴, 赵亚斌, 陈伟, 等. 金属泡沫填充薄壁圆管的轴压载荷位移关系[J]. 力学学报, 2010, 42(6): 1211-1218. LU Zixing, ZHAO Yabin, CHEN Wei, et al. Relation of load and displacement for the metal foam-filled tube during the axial compression[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1211-1218. |
| [11] |
张勇, 闫晓刚, 曾意, 等. 不同冲击工况下蜂窝填充薄壁结构的耐撞性能[J]. 上海交通大学学报, 2019, 53(1): 77-84. ZHANG Yong, YAN Xiaogang, ZENG Yi, et al. Crashworthiness research of honeycomb-filled thin-walled structure under multi-impacting cases[J]. Journal of Shanghai Jiao Tong University, 2019, 53(1): 77-84. DOI:10.16183/j.cnki.jsjtu.2019.01.011 |
| [12] |
LUO C, HAN C Z, ZHANG X Y, et al. Design, manufacturing and applications of auxetic tubular structures: A review[J]. Thin-Walled Structures, 2021, 163: 107682. DOI:10.1016/j.tws.2021.107682 |
| [13] |
任鑫, 张相玉, 谢亿民. 负泊松比材料和结构的研究进展[J]. 力学学报, 2019, 51(3): 656-687. REN Xin, ZHANG Xiangyu, XIE Yimin. Research progress in auxetic materials and structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 656-687. DOI:10.6052/0459-1879-18-381 |
| [14] |
NAIK S, DANDAGWHAL R D, WANI C N, et al. A review on various aspects of auxetic materials a review on various aspects of auxetic materials[J]. AIP Conference Proceedings, 2019, 2105(1): 20004. DOI:10.1063/1.5100689 |
| [15] |
SHUKLA S, BEHERA B K. Auxetic fibrous structures and their composites: A review[J]. Composite Structures, 2022, 290: 115530. DOI:10.1016/j.compstruct.2022.115530 |
| [16] |
GIBSON L, ASHBY M. The mechanics of three-dimensional cellular materials[J]. Proceedings of the Royal Society of London, 1982, 382(1782): 43-59. DOI:10.1098/rspa.1982.0088 |
| [17] |
LAKES R S. Deformation mechanisms of negative Poisson's ratio materials: structural aspects[J]. Journal of Materials Science, 1991, 26(9): 2287-2292. DOI:10.1007/BF01130170 |
| [18] |
GAO Y, ZHOU Z G, HU H, et al. New concept of carbon fiber reinforced composite 3D auxetic lattice structures based on stretching-dominated cells[J]. Mechanics of Materials, 2021, 152: 103661. DOI:10.1016/j.mechmat.2020.103661 |
| [19] |
JOSEPH A, MAHESH V, HARURSAMPATH D. On the application of additive manufacturing methods for auxetic structures: A review[J]. Advances in Manufacturing, 2021, 9(3): 342-368. DOI:10.1007/s40436-021-00357-y |
| [20] |
刘璐. 随机负泊松比泡沫填充薄壁结构设计及力学特性分析[D]. 沈阳: 东北大学, 2019. LIU Lu. Design and mechanical properties analysis of foam filled thin-walled structures wuth random Poisson's ratio[D]. Shenyang: Northeastern University, 2019. |
| [21] |
鲍呈浩, 金浩, 王垠. 点阵结构填充双薄壁管的能量吸收性能研究[J/OL]. 应用力学学报: 1-9[2022-12-02]. http://kns.cnki.net/kcms/detail/61.1112.O3.20221201.1719.005.html. BAO Chenghao, JIN Hao, WANG Yin. Study on energy absorption performance of bitubular square tubes filled with lattice structure[J/OL]. Chinese Journal of Applied Mechanics: 1-9[2022-12-02]. http://kns.cnki.net/kcms/detail/61.1112.O3.20221201.1719.005.html. |
| [22] |
LIU W, HUANG J, DENG X L, et al. Crashworthiness analysis of cylindrical tubes filled with conventional and negative Poisson's ratio foams[J]. Thin-Walled Structures, 2018, 131: 297-308. DOI:10.1016/j.tws.2018.07.004 |
| [23] |
MOHSENIZADEH S, AHMAD Z. Auxeticity effect on crushing characteristics of auxetic foam-filled square tubes under axial loading[J]. Thin-Walled Structures, 2019, 145: 106379. DOI:10.1016/j.tws.2019.106379 |
| [24] |
MOHSENIZADEH S, ALIPOUR R, RAD M S, et al. Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading[J]. Materials & Design, 2015, 88: 258-268. DOI:10.1016/j.matdes.2015.08.152 |
| [25] |
ZHAO X, GAO Q, WANG L M, et al. Dynamic crushing of double-arrowed auxetic structure under impact loading[J]. Materials & Design, 2018, 160: 527-537. DOI:10.1016/j.matdes.2018.09.041 |
| [26] |
GAO Q, GE C Q, ZHUANG W C, et al. Crashworthiness analysis of double-arrowed auxetic structure under axial impact loading[J]. Materials & Design, 2019, 161: 22-34. DOI:10.1016/j.matdes.2018.11.013 |
| [27] |
LI Z B, CHEN R, LU F Y. Comparative analysis of crashworthiness of empty and foam-filled thin-walled tubes[J]. Thin-Walled Structures, 2018, 124: 343-349. DOI:10.1016/j.tws.2017.12.017 |
| [28] |
WIERZBICKI T, ABRAMOWICZ W. On the crushing mechanics of thin-walled structures[J]. Journal of Applied Mechanics, 1983, 50: 727-734. DOI:10.1115/1.3167137 |
 2024, Vol. 32
2024, Vol. 32


