2. 上海交通大学 四川研究院,成都 610042;
3. 上海交通大学 机械与动力工程学院,上海 200240
2. Sichuan Research Institute of Shanghai Jiao Tong University, Chengdu 610042, China;
3. School of Mechanical and Power Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
切削振动是镗孔加工难以避免的问题[1],会降低被加工孔的表面质量[2]。并加速刀片的磨损[3],进一步会浪费生产资源并降低生产效率。减振性能优越的镗杆可以有效降低切削振动,降低生产损失。
减振镗杆主要有主动式、半主动式和被动式3种。主动式减振镗杆利用闭环系统的反馈控制来抑制振动[4],研究人员将压电驱动材料[5]和电磁驱动材料[6]应用于振动控制中,当传感器检测到镗杆发生振动时,控制端将反馈信号通过压电执行器或磁力驱动器输入到系统中,抵消镗杆的振动。半主动式减振镗杆通过使用智能材料组件,如电流变液[7]和磁流变液[8],通过改变电场和磁场的强度来调节智能材料的特性,改变减振系统的性能参数,达到减振的目的。被动式减振镗杆通过改善镗杆的结构和材料来抑制振动[9],具有代表性的是约束阻尼型减振镗杆,其以多种材料代替传统镗杆的单一材料[10],综合发挥这些材料的优势以提升镗杆的减振性能。宋清华等[11]用硬质合金作为约束层、泡沫铝作为阻尼层设计约束阻尼型镗杆,利用硬质合金提升了镗杆的刚度和硬度,利用泡沫铝提升了镗杆的阻尼性能,理论分析和实验证明,提升这些性能对抑制切削颤振和强迫振动具有良好的效果;刘洋等[12]建立了约束阻尼型镗杆静刚度和结构损耗因子的理论公式,通过使用硬质合金、环氧树脂等提升了这两个性能参数,同时对镗杆的结构和材质选择进行了优化;夏峰等[13]利用有限元分析得到了硬质合金、泡沫铝的材料占比对镗杆静刚度、阻尼比及固有频率的影响因子,以降低振幅、提升固有频率为目标对镗杆进行了优化设计,并通过切削实验验证了镗杆的抗振性能。
综上所述,目前针对约束阻尼型镗杆研究的内容和特点如下。首先,价格昂贵、加工困难的硬质合金仍是减振镗杆的主流选择[14-15]; 其次,在对镗杆进行材料优选与结构优化时,优化分析的内容集中在提升镗杆的静刚度[11-12]、固有频率[16]等相对独立的性能参数上,这些参数中的每一个仅能代表镗杆在某一方面的振动特性[10]。
为此,本文设计了一种轻量化复合结构碳纤维复合材料(Carbon Fiber Reinforced Plastic,CFRP)镗杆,使用轻质坚固的CFRP和钢材代替硬质合金,以碳纤维的缠绕角度和复合材料的铺层厚度为镗杆的设计变量,以镗杆的固有频率、静刚度和动刚度为研究和优化对象,从提升动态特性的角度增强镗杆的减振能力。
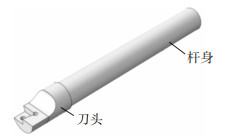
1 CFRP镗杆的设计 1.1 镗杆的结构设计和材料选择本文减振镗杆的设计理念与减振机理如下:使用低密度、高比刚度的CFRP实现镗杆的轻量化[16],通过复合结构将优质钢材与CFRP相结合使镗杆具有较高的静刚度,通过镗杆的结构优化来提升其固有频率频和动刚度,最终设计出高固有频率和高动刚度的轻质减振镗杆。镗杆的形状见图 1,复合结构的组成见图 2。当振动发生时,各层材料会由于形变量不同在CFRP内部产生交变的拉压应力和应变[12],CFRP内部纤维之间的聚合物结合剂则通过做功将振动能转化为低水平的热量并耗散掉。
|
图 1 镗杆外形图 Fig.1 Boring bar shape diagram |
|
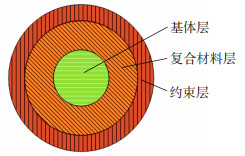
图 2 镗杆复合结构示意图 Fig.2 Schematic diagram of the boring bar composite structure |
在材料选择方面:复合材料层使用高性能40T碳纤维预浸料;基体层和刀头选用调质后的40Cr合金钢,这种材料具有良好的综合力学性能;约束层的主要作用是保护内部材料,需要有防腐蚀、耐氧化的性能,因此,选用304不锈钢。硬质合金镗杆材料选用碳化钨合金。各材料性能参数见表 1。其中,E1为沿碳纤维轴向的弹性模量;E2为垂直于碳纤维轴向的弹性模量;G12为垂直于碳纤维轴向的剪切模量;μ12为沿轴向拉伸碳纤维时,碳纤维的横向正应变与轴向正应变的比。
| 表 1 材料性能参数 Table 1 Material performance parameters |
CFRP减振镗杆的几何尺寸见表 2,其中复合材料层和基体层单边厚度之和为10 mm。由于镗杆的形状与尺寸均会影响其力学性能和受力情况,因此,硬质合金镗杆与CFRP镗杆保持形状一致、尺寸相同。
| 表 2 镗杆尺寸参数 Table 2 Boring bar size parameters |
复合材料层的设计参数为缠绕角度和铺层厚度[12],这些参数会影响复合材料层的力学性能,进而影响镗杆的动态切削性能。0°的碳纤维缠绕角可以增强镗杆的静刚度,而静刚度是镗杆切削稳定性的基本保证之一[17],因此将总占比为50%的碳纤维的缠绕角度设为0°,并将50%的角度设为变量,变化范围设置为15°~75°(碳纤维缠绕角度须在90°以下)[18]。
复合结构CFRP镗杆各层材料的生产加工顺序如下:先加工出基体层(细长杆件,通常采用车削方式进行加工)[16],再将碳纤维预浸料以层层叠加的方式缠绕到基体层上,在真空状态下对复合材料层进行加热固化,使其在基体层上紧固,最后将约束层(圆筒状衬套)通过粘结胶与复合材料层粘结在一起。
在车削加工过程中,杆件的刚度会随着其长度的增加而降低,这容易引发其变形,使其不再适合预浸料的缠绕。经多次切削测试,将基体层的最小半径定为2.5 mm,此时复合材料层的厚度最大,为7.5 mm。将复合材料层的最小厚度取为3.5 mm,厚度参数的间隔定为1 mm[18],具体设计参数见表 3。
| 表 3 复合材料层设计参数 Table 3 Design parameters of composite layer |
根据表 1、2、3可以计算出CFRP镗杆与硬质合金镗杆的质量如表 4所示。
| 表 4 各镗杆的质量 Table 4 Quality of boring bars |
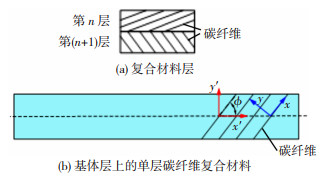
固有频率是决定镗杆振动特性的重要参数,在实际加工中,镗杆的固有频率越高,切削颤振就越难发生[19-20],加工过程就越平稳。本文将建立CFRP镗杆固有频率的计算模型,并结合有限元法对其进行研究。镗杆内部的碳纤维复合材料以层层叠加的方式缠绕在基体层上,由于缠绕角度不同,在进行力学性能计算时,需要先进行本构方程转换,复合材料的缠绕状态示意图见图 3,其中,n为碳纤维复合材料层数。
|
图 3 缠绕在镗杆上的碳纤维复合材料 Fig.3 CFRP wrapped around boring bar: (a) laminated composite layer; (b) monolayer of composite wrapped around substrate layer |
对于缠绕在基体层上的单层碳纤维预浸料,镗杆轴线作为直角坐标系x′-y′的x′轴,预浸料中碳纤维的缠绕轨迹线作为直角坐标系x-y的x轴,x轴和y轴的夹角为ϕ。虽然每层预浸料在自身缠绕轨迹线方向上的力学模量都相同,但每层预浸料的ϕ值不同,需要通过柔度转换矩阵将每层预浸料的力学模量转换到x′轴方向上,转换关系为
| $ \left[\boldsymbol{S}^{\prime}\right]=[\boldsymbol{T}]^{\mathrm{T}}[\boldsymbol{S}][\boldsymbol{T}] $ | (1) |
式中:[S′]为预浸料在x′方向上的柔度矩阵;[S]为预浸料在x方向上的柔度矩阵;[T]为转换矩阵,矩阵元素为
| $ \left[\begin{array}{ccc} \cos ^2 \phi & \sin ^2 \phi & 2 \sin \phi \cos \phi \\ \sin ^2 \phi & \cos ^2 \phi & -2 \sin \phi \cos \phi \\ -\sin \phi \cos \phi & \sin \phi \cos \phi & \cos ^2 \phi-\sin ^2 \phi \end{array}\right] $ |
根据式(1)可以求出矩阵[S′]中的元素值,对该矩阵求逆,便可得出碳纤维预浸料在x′轴方向的刚度矩阵。针对镗杆的复合结构,基于基霍夫假设和复合材料层合板的层压理论[16],其等效抗弯刚度(EI)为
| $ E I=\sum\limits_{n=1}^N \frac{{\rm{\mathsf{π}}}\left[\left(D^n\right)^4-\left(d^n\right)^4\right]}{64} E_{x^{\prime}}^n $ | (2) |
式中:N为镗杆中各层材料的总层数;Dn和dn分别为第n层材料的外直径和内直径,Ex′为第n层材料在x′轴方向的有效工程模量。
复合结构镗杆在切削状态下的受力模型简化为悬臂梁,悬臂梁的无阻尼固有频率f可以根据其等效抗弯刚度进行计算[20]
| $ f=3.516 \sqrt{\frac{E I}{m l^3}} $ | (3) |
式中:m为镗杆的质量;l为镗杆的悬伸长度。
镗杆的有阻尼固有频率f′和无阻尼固有频率f的关系为
| $ f^{\prime}=f \sqrt{\left(1-\zeta^2\right)} $ | (4) |
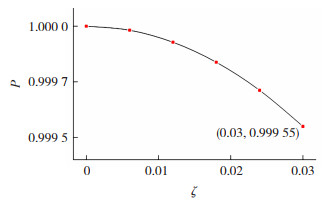
式中:ζ为镗杆的阻尼比。根据式(4),设f′和f的比值为P,P随ζ的变化规律见图 4。
|
图 4 P和ζ的关系 Fig.4 Relationship between P and ζ |
如图 4所示,当阻尼比ζ=0.03时,f′和f之间的差值为f值的0.045%。根据CFRP减振镗杆与硬质合金镗杆的材料阻尼特性,其制成轴件的阻尼比在0.03以内[12-13]。阻尼比对镗杆固有频率的影响很小,此时,镗杆的无阻尼固有频率和有阻尼固有频率是近似相等的。
2.2 CFRP镗杆固有频率的有限元分析通过Abaqus软件对镗杆进行约束模态仿真,镗杆在端头约束状态(镗杆的悬伸量为镗杆的全长)下的仿真结果见图 5,镗杆固有频率的理论计算结果和相对误差见表 5。

|
图 5 镗杆A、B、C、D、E、F、G、H、I的模态振型图 Fig.5 Mode pattern of boring bar A, B, C, D, E, F, G, H and I |
| 表 5 镗杆固有频率的理论计算结果和相对误差 Table 5 Theoretical calculation results and relative error of natural frequencies for boring bar |
如表 5所示,CFRP镗杆固有频率的理论计算结果与有限元仿真结果相对误差的最大值为0.85%,说明这两种结果是比较准确的。硬质合金镗杆固有频率的仿真结果为676.45 Hz。
根据镗杆固有频率的仿真结果绘制关系曲线图,如图 6所示。
|
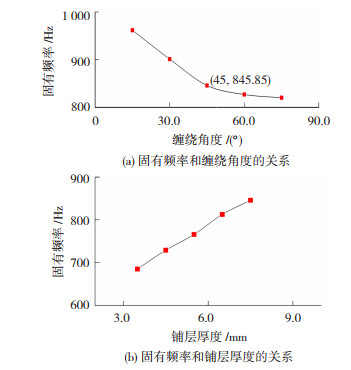
图 6 设计参数对镗杆固有频率的影响规律 Fig.6 Influence of design parameters on natural frequency of boring bar: (a) relationship between natural frequency and winding angles; (b) relationship between natural frequency and laying thickness |
CFRP镗杆的固有频率和碳纤维缠绕角度呈负相关关系,当缠绕角度大于45°时,曲线的下降趋势减缓,说明当缠绕角度在0°~45°的范围内,减小缠绕角度可以更有效地提升镗杆的固有频率。镗杆的固有频率与CFRP铺层厚度呈正相关关系,曲线的变化趋势均匀,表明镗杆的固有频率会随着CFRP厚度的增加而匀速增加,因此,以提升固有频率为目标对镗杆进行评估的结果是:镗杆F的固有频率最高。
3 CFRP镗杆静、动刚度的研究 3.1 CFRP镗杆静刚度计算与实验验证镗杆的静、动刚度分别代表了镗杆的静态力学性和动态力学性能[19],在切削加工中,当切削速度较低时,切削力的频率也比较小,此时的切削力可以视为静态载荷,镗杆抵抗弯曲变形的能力取决于静刚度的大小。但随着切削速度的提升,载荷频率逐渐增大,镗杆的动刚度对其抵抗弯曲变形能力的影响越来越大,动刚度越大,切削振动的强度越小[20]。因此,需要先研究镗杆的静刚度,再建立镗杆的结构动力学模型,从频响函数的角度,对镗杆的动刚度进行分析。
将载荷加载到镗杆的前端端头,镗杆端头挠曲量ymax和镗杆静刚度K′的关系为
| $ K^{\prime}=\frac{F}{y_{\max }} $ | (5) |
式中F为施加在镗杆端头的力。
式(5)表示镗杆的静刚度与端头挠曲量成反比,因此,挠曲量的大小可以直接反映出静刚度的大小,ymax的计算公式为
| $ y_{\max }=\frac{F L^3}{3 E I} $ | (6) |
式中:L为CFRP镗杆的悬伸量;EI可以根据式(1) 和式(2)求出。
令L为165 mm,F为49 N,可得到每根镗杆的端头挠曲量。为了验证计算结果的有效性,通过实验对计算结果进行验证,将质量为5 kg的质量块悬挂在镗杆的端头,镗杆用装夹装置固定,悬伸量为165 mm,用千分表测量镗杆的端头挠曲量,各镗杆端头挠曲量的计算结果、实验结果和相对误差如表 6所示。
| 表 6 镗杆端头挠曲量的计算结果、实验结果及相对误差 Table 6 Calculation results, experimental results and relative errors of deflection of boring bars end |
两种结果的相对误差最大为9.7%,考虑到经验公式带来的误差[18],计算结果是较为准确的。硬质合金镗杆在相同的实验条件下,端头挠曲量为0.014 mm。根据实验结果,结合式(5),各镗杆的实验静刚度值如表 7所示,其变化规律如图 7所示。
| 表 7 各镗杆的静刚度 Table 7 The static stiffness of boring bars |
|
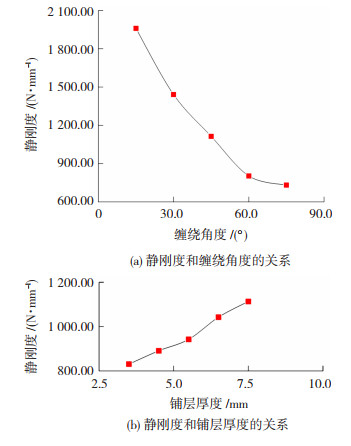
图 7 设计参数对静刚度的影响规律 Fig.7 Influence of design parameters on end deflection amount: (a)relationship between static stiffness and winding angles; (b)rlationship between static stiffness and laying thickness |
根据静刚度曲线,镗杆的静刚度和碳纤维缠绕角度呈负相关关系,与铺层厚度呈正相关关系,说明减小碳纤维角度和增大碳纤维预浸料铺层厚度可以改善镗杆的静刚度。因此,以提升静刚度为目标对镗杆进行评估的结果是:镗杆F的静刚度最大。
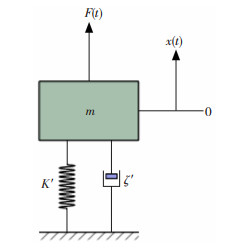
3.2 CFRP镗杆动刚度的研究分析在进行切削加工时,径向切削力导致的径向振动是切削振动的主要来源[3],此时镗杆可以简化为单自由度弹簧振子系统,如图 8所示。
|
图 8 单自由度弹簧振子模型 Fig.8 Single-degree-of-freedom spring oscillator model |
图 8中:F(t)为作用在系统上的载荷;x(t)为系统的位移;K′为系统的静刚度;m为系统的质量;ζ′为系统的阻尼比;系统的固有频率为ωn。该系统用位移表征的频率响应函数表达式为
| $ H(i \omega)=\frac{x(i \omega)}{F(i \omega)} $ | (7) |
式中ω为载荷的频率。
将K′、m、ζ′、ωn代入式(7)可得
| $ H(i \omega)=\frac{1}{-m \omega^2+i 2 \zeta^{\prime} \omega_n \omega+K^{\prime}} $ | (8) |
系统的动刚度K可以表示为
| $ K(i \omega)=\frac{F(i \omega)}{x(i \omega)} $ | (9) |
因此,动刚度K可以进一步表示为
| $ K=-m \omega^2+i 2 \zeta^{\prime} \omega_n \omega+K^{\prime} $ | (10) |
由式(10)可知,镗杆的动刚度包含了质量、固有频率、静刚度和阻尼比这些参数,是具有较强综合性的表征参数。将CFRP镗杆A、C、E、F和硬质合金镗杆的静刚度K′、固有频率ωn和质量m代入式(10),任取镗杆的阻尼比ζ′为0.01和0.02,绘制镗杆在频域内动刚度的变化曲线,如图 9所示。
|
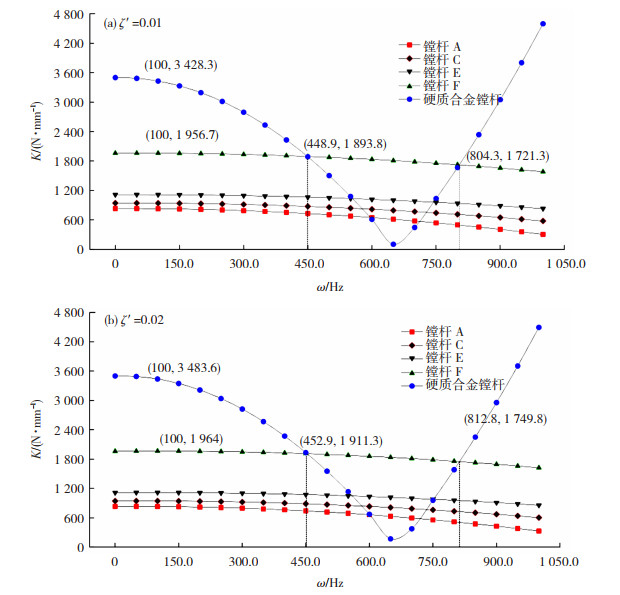
图 9 硬质合金镗杆与CFRP镗杆的动刚度曲线 Fig.9 Dynamic stiffness curves of tungsten boring bar and CFRP boring bars |
从动刚度曲线的整体变化趋势看,硬质合金镗杆会先下降再提升,且其下降和提升的速度都很快,而所有的CFRP镗杆都会以平稳的速度缓慢下降,这表明与硬质合金镗杆相比,CFRP镗杆更能够使动刚度在载荷频率变化时保持稳定,这使得CFRP镗杆在频率由小变大的整个加工过程中,可以保持稳定的抗弯曲变形的能力,可以更稳定地进行切削加工。同时,在一定的频率范围内,CFRP镗杆的动刚度会超过硬质合金镗杆的动刚度,以镗杆F为例,当ζ′=0.01时,该频率范围为448.9~804.3 Hz,占整个频率范围的35.54%,当ζ′=0.02时,该频率范围为452.9~812.8 Hz,占整个频率范围的35.99%。此时,CFRP镗杆F比硬质合金镗杆的加工更加平稳,产生的切削振动的振幅更小。
根据式(10)的函数特性,可以研究镗杆的性能参数对动刚度曲线的影响规律。在式(10)中,静刚度K′是常系数项,因此K′不会影响动刚度曲线的变化趋势,但会与变化趋势一起影响动刚度整体水平的大小,以镗杆F为例,镗杆F的静刚度为1 960 N/mm,在所有CFRP镗杆中最大,并且所有CFRP镗杆动刚度均比较稳定,因此, 镗杆F的动刚度曲线处于所有的CFRP镗杆之上。
在式(10)中,质量m是二次项系数,固有频率ωn是一次项系数,因此,减小m和ωn的值都有利于使动刚度曲线更加平稳,但ωn的作用比较微弱,减小m的效果更加明显,这同时也证明了镗杆的轻量化设计确实有利于提升镗杆的切削稳定性。以镗杆F和硬质合金镗杆为例,虽然镗杆F的固有频率比较高,但其质量是最小的,因此其动刚度曲线比较平稳。而硬质合金镗杆的固有频率虽然低,但其质量是CFRP镗杆的4~5倍,因此其动刚度曲线变化幅度最大。
对于阻尼比ζ′,在图 9硬质合金镗杆的动刚度曲线中,当ω=100 Hz时,两点对应的动刚度的差值仅为10.3 N/mm,而在镗杆F的动刚度曲线中,该差值仅为7.3 N/mm,不难看出,阻尼比ζ′对动刚度曲线的影响非常小。
根据图 9可知,以提升动刚度为目标对镗杆的结构进行优化分析的结果是:镗杆F的动刚度最大。综合考虑各项性能参数,对镗杆进行优化分析的最终结果是:镗杆F在当前设计下减振效果最佳。将硬质合金镗杆命名为Y,通过镗杆F和硬质合金镗杆Y的振动加工实验来验证镗杆F的减振性能。镗杆F和Y的实物如图 10和图 11所示。

|
图 10 镗杆F的样品与截面示意图 Fig.10 Schematic of sample and section of boring bar F |

|
图 11 镗杆Y的样品与截面示意图 Fig.11 Schematic of sample and section of boring bar Y |
本实验通过测量镗杆F和Y在加工时的振动信号,比较出两根镗杆切削振动的强弱,从而衡量二者的减振性能。根据本文的分析,两根镗杆减振性能不同的主要原因在于,当载荷频率变化时,保持动刚度稳定性的能力不同,因此,控制载荷频率变化是本实验的关键,由于载荷频率与切削速度成正比[21],因此,在设计切削参数时,将切削速度作为主要变量进行研究。
同样,振动信号要选择对载荷频率变化较为敏感的,在众多振动信号中,加速度信号同时考虑了振动幅值、振动频率和频率变化,是对频率敏感性最高的振动信号,因此,用吸附在镗杆上的单向加速度传感器测量镗杆的径向加速度信号,再通过信号分析仪和CUTPRO软件对信号进行处理[12]。
本实验的切削参数如表 8所示,实验设备及其相关参数如表 9、图 12所示。
| 表 8 切削参数 Table 8 Cutting parameters |
| 表 9 实验设备及相关参数 Table 9 Experimental equipment and relevant parameters |

|
图 12 实验设备 Fig.12 Test equipments: (a)machining machine; (b)vibration signal measurement equipment |
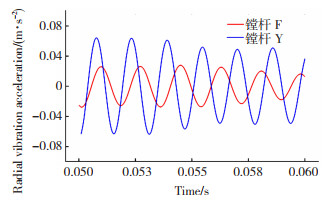
将镗杆的悬伸量设置为130 mm,在切削速度为165 m/min,背吃刀量为0.05 m,进给量为0.1 mm/r时,两根镗杆的切削加工处于较为稳定状态下的径向加速度的测量结果如图 13所示。
|
图 13 径向振动加速度曲线 Fig.13 Radial vibration acceleration curve |
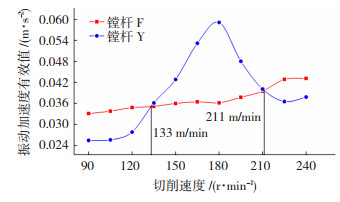
振动加速度有效值(RMS值)与振动能量的关系最大[12],因此,将表 8中的每组切削参数均重复加工3次,将3次加工中两根镗杆都处于较为稳定加工状态下,测得的径向加速度RMS值的平均值作为衡量两根镗杆振动强度的标准,作出该值与切削速度的关系曲线如图 14所示。
|
图 14 振动强度曲线 Fig.14 Vibration strength curve |
根据图 14,从整体趋势上来看,虽然镗杆F的加速度RMS曲线会随着切削速度的增加而上升,但上升的趋势较为缓慢且稳定,而硬质合金镗杆Y的加速度RMS曲线则在迅速上升后迅速下降,这是由于在切削加工时,硬质合金镗杆的动刚度更容易受到载荷频率影响而产生波动,当其动刚度较小时,动态切削力会使其产生振幅较大、强度较高的振动,而CFRP镗杆则由于更具有保持动刚度稳定的能力,使其在整个切削加工过程中保持了良好的切削稳定性。也正是由于这一原因,当切削速度增加到133~211 m/min范围时(约占整个加工过程切削速度范围的52%),镗杆F的振动强度才会低于镗杆Y,从而具备更好的减振性能。
综上,因为CFRP镗杆可以在载荷频率变化时更好地维持自身动刚度的稳定性,所以其减振性能可以在52%的切削速度范围内强于硬质合金镗杆。
5 结论1) 本文以轻质坚固的40T型碳纤维复材为主要材料,设计了一种静刚度略小于而固有频率大于硬质合金镗杆的轻量化复合结构CFRP镗杆。
2) 利用镗杆的频响函数推算出其动刚度特性方程,作出设计参数不同的CFRP镗杆和硬质合金镗杆的动刚度曲线图,研究了不同设计参数对镗杆动刚度的影响效果:镗杆具备较大的静刚度是维持其本身具备较高动刚度的前提;减小质量可以有效减缓镗杆动刚度降低的速率;减小固有频率和增大阻尼比虽然也有利于维持镗杆的动刚度稳定,但其影响相对较小。
3) 不同镗杆动刚度曲线图的研究结果显示,质量较小的CFRP镗杆远比硬质合金镗杆更能够在承受动载荷时将动刚度维持在较高的水平。为了验证相关结论,挑选出优化后的CFRP镗杆和硬质合金镗杆进行振动加工实验,实验以振动加速度有效值(RMS值)作为衡量镗杆振动强度的标准,实验结果表明:在切削速度提升过程中,CFRP镗杆的RMS值维持在相对稳定的水平,表现出更加稳定的切削特性,并且在52%的切削速度范围内的振动RMS值低于硬质合金镗杆,表现出更好的减振能力。
| [1] |
SALEH M, NEJATPOUR M, ACAR H Y, et al. A new mag-netorheological damper for chatter stability of boring tools[J]. Journal of Materials Processing Technology, 2020, 289(1): 116931. DOI:10.1016/j.jmatprotec.2020.116931 |
| [2] |
LU Xiaodong, CHEN Feng, ALTINTAS Y. Magnetic actuator for active damping of boring bars[J]. CIRP Annals Manufacturing Technology, 2014, 63(1): 369-372. DOI:10.1109/TMECH.2015.2393364 |
| [3] |
TIAN Xiaoqing, CHEN Ruofeng, JIANG Hong, et al. Detection and visualization of chatter in gear hobbing based on combination of time and frequency domain analysis[J]. International Journal of Advanced Manufacturing Technology, 2020, 111(3): 1-12. DOI:10.1007/s00170-020-06120-0 |
| [4] |
FALLAH M, MOETAKEF-IMANI B. Investigation on nonlin-ear dynamics and active control of boring bar chatter[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43(3): 1116-1143. DOI:10.1007/s40430-021-02808-w |
| [5] |
MATSUBARA A, MAEDA M, YAMAJI I. Vibration suppression of boring bar by piezoelectric actuators and LR circuit[J]. CIRP Annals-Manufacturing Technology, 2014, 63(1): 373-376. DOI:10.1016/J.CIRP.2014.03.132 |
| [6] |
CHEN Feng, LIU Guangya. Active damping of machine toolvibrations and cutting force measurement with a magnetic actuator[J]. International Journal of Advanced Manufacturing Technology, 2017, 89(1): 691-700. DOI:10.1007/s00170-016-9118-y |
| [7] |
SINGARAVELU C, VARATHARAJAN P, RAMU G, et al. Investigation of damping characteristics on copper-based shape memory alloy frictional damper in boring process[J]. Arabian Journal for Science and Engineering, 2021, 21(6): 501-512. DOI:10.1007/s13369-021-05719-z |
| [8] |
HAYATI S, SHAHROKHI M, HEDAYATI A. Development of a frictionally damped boring bar for chatter suppression in boring process[J]. International Journal of Advanced Manufacturing Technology, 2021, 113(9): 2761-2778. DOI:10.1007/s00170-021-06791-3 |
| [9] |
HAYATI S, HAJALIAKBARI M, RAJABI Y, et al. Chatter reduction in slender boring bar via a tunable holder with variable mass and stiffness[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 2017, 232(12): 2098-2108. |
| [10] |
BONDA A, SRINIVAS J, NANDA B K. Investigation of stability in internal turning using a boring bar with a passive constrained layer damping[J]. FME Transactions, 2021, 49(2): 384-394. DOI:10.5937/fme2102384Y |
| [11] |
SONG Qinghua, SHI Jiahao, LIU Zhanqiang, et al. Boring bar with constrained layer damper for improving process stability[J]. International Journal of Advanced Manufacturing Technology, 2016, 83(9): 1951-1966. DOI:10.1007/s00170-015-7670-5 |
| [12] |
刘洋, 刘战强, 宋清华. 约束阻尼型镗杆的优化及减振性能[J]. 航空学报, 2016, 37(6): 1992-2002. LIU Yang, LIU Zhanqiang, SONG Qinghua. Optimization and damping performance of constrained damping boring bar[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1992-2002. DOI:10.7527/S100-6893.2015.0241 |
| [13] |
夏峰, 刘战强, 宋清华. 约束阻尼型镗杆的优化及减振性能[J]. 航空学报, 2014, 35(9): 2652-2659. XIA Feng, LIU Zhanqiang, SONG Qinghua. Optimization and damping performance of constrained damping boring bar[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2652-2659. DOI:10.7527/s1000-6893.2013.0484 |
| [14] |
GUO Haiwei. The design and optimization of carbon fiber epoxy matrix composite boring bar[J]. Manufacturing Technology & Machine Tool, 2019, 35(1): 101-104. DOI:10.19287/j.cnki.1005-2402.2019.01.019 |
| [15] |
马伯乐, 任勇生, 张玉环, 等. 旋转镗杆切削颤振稳定性预测[J]. 振动与冲击, 2019, 38(16): 115-122. MA Bole, REN Yongsheng, ZHANG Yuhuan, et al. Stability prediction of rotating boring bar[J]. Journal of Vibration and Shock, 2019, 38(16): 115-122. DOI:10.13465/j.cnki.jvs.2019.16.017 |
| [16] |
SUN Zeyu, XIAO Jie, YU Xuduo, et al. Vibration charac-teristics of carbon-fiber reinforced compositedrive shafts fabricated using filament winding technology[J]. Composite Structures, 2020, 7(241): 111725. DOI:10.1016/j.compstruct.2019.1125 |
| [17] |
LI Lie, SUN Beibei, HUA Haitao. Analysis of the vibraton characteristics of a boring bar with a variable stiffness dynamic vibration absorber[J]. Shock and Vibration, 2019, 19(9): 2501-2513. DOI:10.1155/2019/5284194 |
| [18] |
郭海伟. 复合材料减振镗杆参数设计与加工精度实研究[D]. 北京: 中国矿业大学, 2020. GUO Haiwei. Parametric design and machining accuracy test of composite damping boring bar[D]. Beijing: China University of Mining and Technology, 2020. |
| [19] |
AIMINI P N, MOETAKEF-IMANI B. Highperformance controller design and evaluation for active vibration control in boring[J]. Scientia Iranica, 2019, 29(5): 2839-2853. DOI:10.1016/j.eng.2021.03.022 |
| [20] |
SUI He, ZHANG Lifeng, WANG Shuang, et al. Feasibility study on machining extra-large aspect ratio aviation deep-hole Ti6Al4V part with axial ultrasonic vibration-assisted boring[J]. International Journal of Advanced Manufacturing Technology, 2021, 118(11): 3995-4017. DOI:10.1007/s00170-021-08212-x |
| [21] |
PENG Huanghu, XU Hao, WU Yijie, et al. Research on multi-parametric coupling design method of deformable boring bar in embedded giant magnetostrictive actuator[J]. International Journal of Precision Engineering and Manufacturing, 2020, 21(12): 2234-2245. DOI:10.1007/s12541-020-00414-9 |
 2024, Vol. 32
2024, Vol. 32


