2. 浙江省零件轧制成形技术研究重点实验室,浙江 宁波 315211
2. Part Rolling Key Laboratory of Zhejiang Province, Ningbo 315211, China
钛合金材料具有优异的比强度、比刚度和耐腐蚀等特性,因而备受航空、航天、交通等行业的青睐[1-2]。采用Ti-45Nb钛合金材料制作紧固件在航空领域已得到了广泛应用[3]。紧固件常使用冷镦加工,目前多道次冷镦成形技术快速发展,相较于其他加工工艺,冷镦成形具有很大的优势:冷镦成形件尺寸精度高, 生产效率高以及冷镦成形材料利用率高等[4-5]。但在冷镦成形的紧固件中,尤其是对于较难成形的薄壁长管类零件,其大长径比的特征在常规的冷镦成形时常会出现套管破裂、头部折叠以及表面粗糙等缺陷,并且在成形薄壁件时模具的损耗也会增加。如何减少成形应力、减少模具磨损以及提高产品质量是亟待解决的问题。有研究表明:振动辅助成形技术既可以降低成形压力,也可以提升零件成形质量[6]。振动辅助成形技术是近20年发展的新型技术,其具有近净成形、加工难变形金属的潜力,最早被应用在拉拔工艺中,后续在振动辅助板料成形、挤压等其他工艺中也逐渐得到了发展,被应用于铝、钛、铜、钢等材料的成形中[7]。一直以来,研究者不断通过实验对振动辅助成形技术进行研究,并结合实验建立可靠的理论模型。但随着计算机技术的发展,采用仿真模拟技术研究振动辅助成形工艺的方法方兴未艾。在振动辅助成形本构理论研究方面,Kirchner等[8]建立了与弹塑性应变率无关材料和应变率相关材料的压缩应力振荡叠加分析模型,研究表明: 在低频振动辅助下,对于应变率无关的材料, 平均应力将低于静态应力;而对于应变率相关的材料, 有可能低于或一致或高于静态应力。蔡改贫等[9]依据Kirchner对应变时间历程的基本假设,建立了振动辅助拉伸的本构模型,研究表明,采用粘弹塑性模型描述金属材料在振动条件下的力学性能具有较好的预测能力。王家鹏等[10]从超声振动辅助成形机理出发,结合蔡改贫教授所用率相关的粘弹塑性模型建立了6061铝合金的本构模型。陈晓晓等[11]在渐进成形中基于晶体塑性理论,在考虑声软化效应后建立了本构模型,研究表明,改进后的材料本构模型较以往的模型在精度上有了很大提高。
近几年来,国内外学者不断通过数值模拟和实验的方法对模具优化进行大量的研究。温诗铸[12]对材料磨损研究的进展进行了总结,提出使用先进的理论和测试手段可从深层次揭示磨损机制及其本质,从而建立普适性较强的宏观磨损准则。张剑寒等[13]使用正交试验法研究了冷镦模具、工艺参数对钢球成形质量的影响,得到最优的工艺方案。丛兵兵等[14]利用Deform有限元软件对马车螺栓冷镦成形过程进行模拟,分析了各工步毛坯材料在模具内的流动情况以及毛坯成形缺陷与模具结构的相关性,并对模具结构进行优化设计,使模具的受力情况得到改善。Fernandes等[15]利用有限元方法对管状螺钉的成形过程进行研究,完善了螺钉成形工艺,优化了模具结构,解决了管状预制棒的塑性变形和模具的弹性变形问题。André等[16]从摩擦的角度出发,对杆件的冷正挤压进行了有限元模拟,在变形过程的各个阶段分析了摩擦参数对模拟力-位移曲线的影响,研究发现,恒定摩擦系数和恒定摩擦应力参数可适用于研究成形过程。
Lin等[17]对Ti-45Nb钛合金试样进行了低频振动辅助镦粗实验,研究发现:施加振动后,Ti-45Nb的变形均匀性得到提高,流动应力显著降低,且振动频率和振幅越大,流动应力降低现象越明显;且振动辅助Ti-45Nb铆钉的成形,可以有效降低成形力和裂纹概率。本文将依据Lin等所进行的低频振动辅助镦粗实验研究结果,研究Ti-45Nb钛合金材料在振动辅助冷镦条件下的本构模型,并利用数值模拟技术对钛合金材料冷镦成形进行分析,优化模具结构。
1 振动辅助钛合金Ti-45Nb多道次冷镦成形的粘弹塑性本构方程 1.1 钛合金Ti-45Nb塑性成形本构模型基于晶体塑性理论中宏观的连续介质力学与运动学的结合,根据现有的粘弹塑性理论建立模型,可以准确地描述材料的应力应变关系,清楚地反映材料在塑性变形过程中的物理变化。描述钛合金材料粘弹塑性行为的力学模型可以由弹簧模型和粘壶模型组合。综合考虑材料粘弹性和粘塑性变形影响的应力叠加混合模型如图 1所示。

|
图 1 粘弹塑性模型图 Fig.1 Visco-elasticity plasticity model |
由图 1可知,振动辅助冷镦成形热力耦合本构模型假设由两个微观机制构成:第①部分主要描述振动的应力叠加效应,将模型分为粘弹性部分与粘塑性部分串联;第②部分表示的是金属变形过程中的材料软化。
在机制①中,应力分解为粘弹性部分和粘塑性部分,由能量平衡与熵不平衡来表示材料的变化过程:在弹性阶段,塑性应变不发生,其总应力可采用弹性第二皮奥拉应力表示[9]。当材料发生屈服时,进入塑性阶段,总应变是弹性应变与塑性应变的叠加,其中应变包含了振动导致的反复加载和卸载。
在机制②中,采用Maxwell单元反映材料的软化变化,其中以粘壶表示在金属成形过程中金属位错密度与应变率相关的变化。
1.1.1 自由能在连续介质力学的热力学框架下,用一个简单的线弹性形式来表示自由能,
| $ \bar{\psi}^{(1)}=\frac{1}{2} E \varepsilon^2-E \alpha\left(\theta-\theta_0\right) \varepsilon+\tilde{f}(\theta) $ | (1) |
式中:E为弹性模量;ε为应变率;α为热膨胀系数;θ为温度;θ0为初始温度;
| $ \sigma^{(1)}=\frac{\eta_1}{\eta_1+\eta_2} E \varepsilon+\frac{\eta_1 \eta_2}{\eta_1+\eta_2} \dot{\varepsilon}+\sigma_i $ | (2) |
式(2)中:等式右边第1项表示在振动条件下弹性应力变化;第2项表示振动条件下粘性应力的变化,可以体现出振动的应力叠加效应,即在原有应力应变基础上叠加周期性的波动;第3项σi表示塑性应力部分,金属塑性变形以滑移为主,滑移是借助位错在滑移面上的运动来逐步进行的。位错的运动导致位错密度的变化,其在能量平衡中对塑性变形项作出了重要贡献。
1.1.2 塑性流动速率首先定义一个阻抗
| $ \begin{aligned} S_{\mathrm{a}}= & S_0(\theta)+S_{\mathrm{f}}(\theta)+S_{\mathrm{HP}}= \\ & K_0 \exp (-\theta /B)+\beta \mu(\theta) b \sqrt{\rho}+K_{\mathrm{HP}} d^{1 /2} \end{aligned} $ | (3) |
式中:
| $ \mu(\theta)=\mu_0-\frac{e}{\exp \left(\theta_0 /\theta\right)-1} $ | (4) |
式中:e为材料常数;θ0为参考温度。
等效压缩塑性应变率
| $ \dot{\bar{\varepsilon}}^p=\left\{\begin{array}{cc} 0 & \bar{\sigma} \leqslant S_{\mathrm{a}} \\ \dot{\varepsilon}_0 \exp \left[-\frac{\Delta Q}{k_{\mathrm{B}} \theta}\left(1-\left(\frac{\bar{\sigma}}{\sigma_i}\right)\right)^p\right]^q & \bar{\sigma}>S_{\mathrm{a}} \end{array}\right. $ | (5) |
式中:
对于绝大部分的金属材料,当应变率范围在10-4~104时,其塑性变形的主要形式为位错的运动,在位错运动过程中,位错之间以及位错和其他障碍之间会发生作用。位错可以在外力作用下产生运动,也能够在热能的作用下克服障碍而运动。
由于位错的交互作用,流动应力中的塑性激活分量可看成是长程障碍引起的内部应力和短程障碍引起的等效应力,可以表示为[18]
| $ \sigma_i=M a G b \sqrt{\rho}\left(\frac{\dot{\bar{\varepsilon}}^p}{\dot{\bar{\varepsilon}}_0}\right)^{1 /m} $ | (6) |
式中:M为泰勒因子,取决于材料的织构,通常取为常数3.06;a为塑性激活分量系数;对于一般的金属材料,伯氏矢量b取0.286 nm;m是材料常数。
参考Mecking和Kocks[19]建立的预测金属位错密度的变化模型,塑性变形过程中,位错演化规律可表示为
| $ \frac{\mathrm{d} \rho}{\mathrm{d} \varepsilon}=M k_1 \sqrt{\rho}-k_2 \rho $ | (7) |
式中:位错存储系数k1视为一个常数;k2为动态恢复系数。
对于多道次冷镦成形,静态回复具有重要意义,必须包含在模型中。静态回复可以通过在位错密度演化方程中引入一个额外的项来解释[20]。
| $ \rho=-k_3 \rho^n \exp \left(-\frac{Q_{\mathrm{s}}}{R \theta}\right) $ | (8) |
式中:
材料在塑性变形过程中收到的背应力可以表示为
| $ \sigma_{\text {back }}=\frac{3}{2} C \ln A $ | (9) |
其中,C为背应力模量,内部缺陷能量A的演化方程可以表示为
| $ A=2 A D^p-\gamma A \ln A \dot{\varepsilon}^p, A(0)=1 $ | (10) |
式中:Dp为塑性变形率,γ≥0是A的动态恢复决定的本构参数。
另外,由于振动的作用引起的应力降低可以表示为
| $ \sigma^{(2)}=-2 \hat{\tau} \varphi\left(E_{\mathrm{u}} /\hat{\tau}\right)^\lambda $ | (11) |
式中:φ和λ为振动能场参数;为材料的剪切阈值;Eu为超声能,其表达式为
| $ E_{\mathrm{u}}=\zeta_{\mathrm{Ti}}^2 \omega^2 \rho_{\mathrm{Ti}} \alpha_{\mathrm{t}} $ | (12) |
式中:ζTi为振幅;ω为振动圆频率;ρTi为材料密度;αt为透射系数。
钛合金Ti-45Nb的材料参数如表 1所示。
| 表 1 Ti-45Nb的材料参数 Table 1 Parameters of Ti-45Nb material |
综上所述,钛合金Ti-45Nb在振动辅助冷镦挤压时,首先会发生粘弹性变形,此时的应力与材料的弹性模量,粘度系数相关。然后在到达屈服极限时,材料发生屈服,产生塑性应变。一方面,随着塑性应变的不断增加,材料位错密度也逐渐增加,同时滑移抗力也随之增加。另一方面,随着振动的作用,材料发生软化,应力下降。本构模型材料参数可根据振动辅助冷镦成形实验数据拟合得到。
1.2 本构模型参数拟合受到振动的影响后,位移加载历程可以表示为一个正弦函数,
| $ X(t)=A_{\mathrm{R}} \sin (2 \pi f t)+v t $ | (13) |
式中: AR为振幅,mm; f为振动频率,Hz; v为加载速度,mm/min; t为加载时间,s。
本文通过尝试法拟合出在振动辅助冷镦成形条件下的材料参数数据。计算开始时,需要先给定材料参数,状态变量初始化,随着应变的增加,内变量演化,应力不断的更新迭加,直至材料产生塑性变形,随后材料的位错密度更新,以及材料滑移抗力的更新。在计算过程中,通过时间增量来求解相关时间微分增量段内的材料应力应变关系,随着时间迭加,不断的更新应变、内变量及应力数据。
MATLAB计算主程序流程如图 2所示
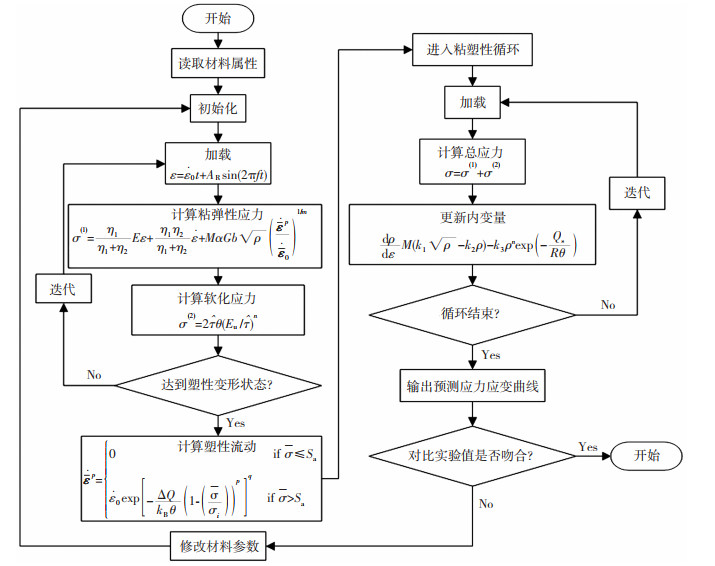
|
图 2 MATLAB主程序流程图 Fig.2 MATLAB main program flow chart |
由图 2可知,在给定材料参数预先取值范围内,MATLAB计算出相应的应力应变曲线并与实验数据进行比较。若误差满足要求,结束计算,得到本构方程中的材料参数。本构模型中材料参数以及拟合的材料参数分别列于表 2、表 3中。用于比较的实验数据为表 4中的F1-1组所得到的数据。
| 表 2 钛合金Ti-45Nb材料本构模型材料参数 Table 2 Material parameters of constitutive model for Ti-45Nb titanium alloy |
| 表 3 钛合金Ti-45Nb材料本构模型拟合的材料参数 Table 3 Material parameters fitted by material constitutive model for Ti-45Nb titanium alloy |
图 3给出了两种不同振动频率工艺参数条件下流变应力计算值与实际实验值的对比图,本文实际实验值参考了文献[17]中的实验内容。该实验原材料为Ti -45Nb丝材,直径为4 mm,高度为5 mm。具体实验方案如表 4所示。0-0组作为对照组,采用传统的压缩方式,压缩过程中不施加振动。编号为F的3组数据代表不同频率的压缩实验,设置振幅为0.1 mm,频率分别为10、20和30 Hz。编号为A的3组数据为不同振幅下的压缩实验,设置频率为10 Hz,振幅分别为0.05、0.10和0.20 mm,其中A2-2与F1-1组实验参数相同。
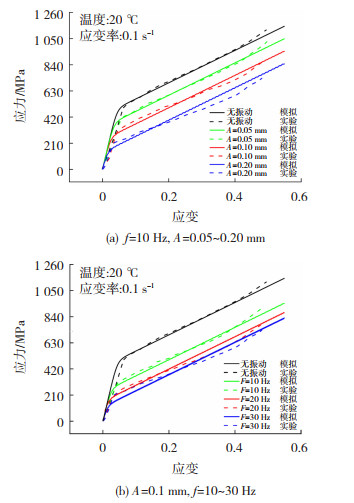
|
图 3 不同振动条件下的模型预测与实验数据对比图 Fig.3 Comparison between model prediction and experimental data under different vibration conditions |
图 3(a)和(b)分别为不同振动幅值和振动频率对压缩实验的影响,可以看到,计算值很好地拟合了振动辅助冷镦成形工艺条件下的Ti-45Nb钛合金应力应变曲线,具有较高的精确度。本构模型定量描述了振动软化作用,并且从图中可以看出振动带来的软化作用在材料塑性变形阶段更为明显。
此外,为了量化该本构模型的预测精度,采用相对系数(RC)对表 4中F1-1组实验模型的预测精度进行评估,评估公式为
| $ \mathrm{RC}=\frac{\sum\limits_{i=1}^n\left(E_i-\bar{E}\right)\left(P_i-\bar{P}\right)}{\sqrt{\sum\limits_{i=1}^n\left(E_i-\bar{E}\right)^2 \cdot \sum\limits_{i=1}^n\left(P_i-\bar{P}\right)^2}} $ | (14) |
式中: E和P为实验曲线和预测曲线中的应力值,E、P为平均值。
通过公式(14)计算模型的值与实验值得出线性相关系数,结果如图 4所示。
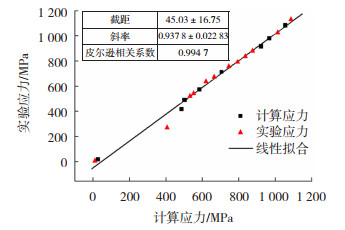
|
图 4 预测误差图 Fig.4 Prediction error diagram |
由图 4可以看到RC的值大于0.994,这表明所建立的本构方程具有较好的拟合效果。
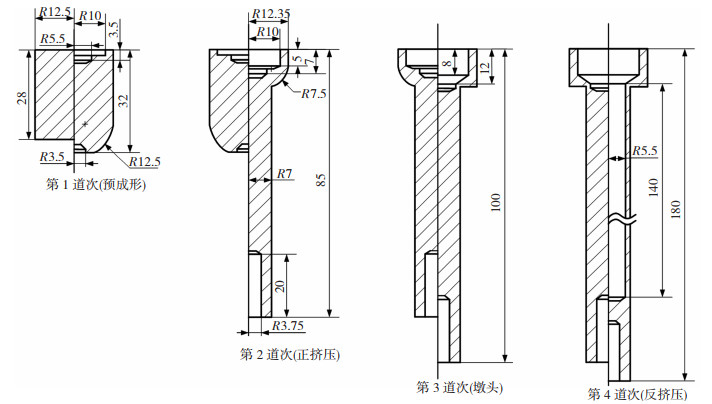
2 振动辅助冷镦成形有限元仿真 2.1 钛合金Ti-45Nb大长径比零件冷镦成形工艺图 5所示为某航空用薄壁零件,材料为钛合金Ti-45Nb。零件头部是整个零件的重要组成部位,为了避免头部在冷镦时出现折叠现象,需要在正挤压道次前增加头部预成形道次。如图 6所示,该多道次工艺分为4个阶段,分别为预成形阶段,正挤压成形阶段,头部成形阶段,反挤压薄壁套管成形阶段。
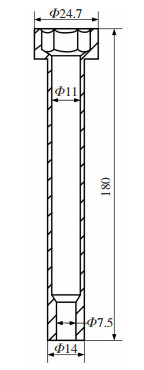
|
图 5 内六角阶梯大长径比零件图(单位:mm) Fig.5 Part drawing of inner hexagon step with large aspect ratio |
|
图 6 内六角阶梯大长径比零件冷镦成形工艺图(单位:mm) Fig.6 Cold heading forming process of inner hexagonal step part with large aspect ratio |
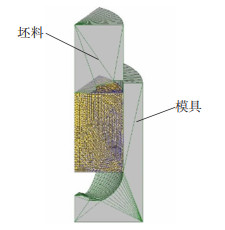
坯料初始直径为25 mm,长度为28 mm,其他参数如表 5所示。在SolidWorks中进行建模,将建好的模型以.STL文件格式导入到有限元软件中。冷镦成形模具及毛坯网格划分模型如图 7所示,由于零件为轴对称零件,Deform软件可以设置对称面,因此采用1/6模型,以提高有限元软件的运算效率。
| 表 5 有限元仿真参数 Table 5 Finite element simulation parameters |
|
图 7 第1道次坯料和模具1/6模型 Fig.7 First pass billets and molds 1/6 mode |
坯料模型采用塑性材料模型,选用1.2节推导的钛合金Ti-45Nb的本构模型,冷镦环境温度设为20 ℃。网格划分采用最小网格,边长约为0.5 mm,网格数目为10 000个。然后,导入模具文件,模具为刚性材料模型,设置模具材料为H-13。为了研究模具的磨损情况,还需将模具也划分网格,网格数目为1 000个,并设置上、下模具和坯料的接触属性。
此外,还需对凸模设置振动辅助,设置振动方向为轴向,进给速度根据全自动高速螺丝打头机设备参数换算得到,设置为75 mm/s[21], 并设置振动参数,振动振幅10~50 μm,频率500~1 000 Hz。由于Deform软件无法定义位移函数,因此设置振动条件时,为了保证离散后仍具有周期函数特性,需将位移函数做离散化处理,然后在前处理的凸模工具动作中选择行程函数并导入离散化公式(13) 的位移-时间数据集。
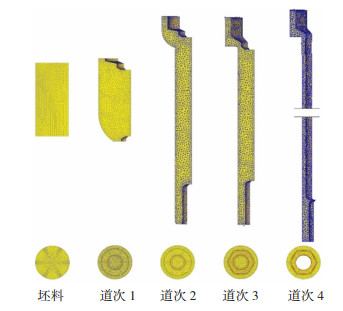
2.3 仿真结果分析经过DEFORM软件模拟冷镦成形后,可以在后处理界面看到各道次的成形状态,检查可能出现的缺陷。如图 8所示,有限元软件很好地模拟出振动辅助多道次冷镦成形过程。
|
图 8 冷镦成形各道次成形情况 Fig.8 Cold heading forming of each pass forming |
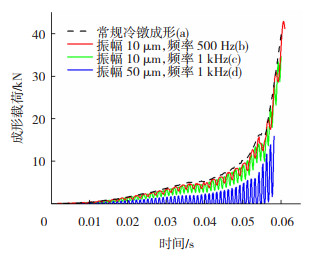
为了研究振动对零件成形载荷的影响,以预成形道次为例,固定上模的进给速度为75 mm/s,对其施加不同频率和振幅的振动。选取4组参数进行比较,得到的成形载荷-时间曲线如图 9所示。
|
图 9 不同条件下冷镦预成形力随时间的变化对比图 Fig.9 Comparison diagram of change of cold heading preforming force with time under different conditions |
图 9中振幅为10 μm的b曲线和c曲线,由于模具进给速度75 mm/s大于临界进给速度vm,所以坯料和模具持续保持接触,因此成形载荷的最小值不等于0。若振幅和频率增大使得临界进给速度vm大于模具进给速度,如图 9中的d曲线,50 μm的振幅,1 kHz的频率使得临界进给速度vm大幅增加,超过了模具进给速度,因此,在振动周期的某个时刻,模具与坯料会发生短暂分离,即完全卸载。曲线b为振幅10 μm,频率500 Hz的成形载荷曲线,相较于曲线a,其成形载荷随位移振荡,但平均成形载荷下降。对比曲线c和d可以发现,相同频率条件下,振幅增加,成形载荷的波动幅度也增加,成形载荷降低明显。综上所述,振动频率和振幅的增加导致零件平均成形载荷降低。
图 10为常规与振动辅助冷镦成形4道次应力分布云图,可以发现各道次的最大应力位置没有发生变化,但最大应力值减小了,各道次最大应力值分别下降了25.3%,35.2%,19.6%,32.2%,振动辅助的引入有效降低了坯料的内部应力。
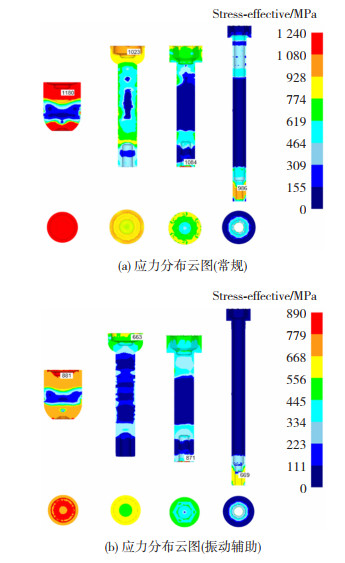
|
图 10 各道次应力分布云图 Fig.10 Stress distribution nephogram of each pass |
相较于整形,正挤压和冷镦头部道次,反挤压道次的变形程度最大,在设计模具时需要特别注意模具的承受能力。在反挤压成形薄壁套管时,由于成形后长径比较大,模具磨损快,寿命非常短。因此,针对模具磨损较快的区域,可在保证金属流动性能和产品质量的前提下,通过改变模具的结构,降低模具应力集中,进而减少模具损耗,提高模具寿命。
3 反挤压道次模具尺寸优化设计 3.1 反挤压道次有限元仿真由于反挤压工艺坯料与模具的接触面非常多,因此振动辅助反挤压过程中的摩擦力减小不可忽略。在振动条件下,整合各个区域的摩擦系数,最终得到零件与模具之间的总摩擦系数[22]
| $ \mu_{\mathrm{ec}}=\mu\left(1-\frac{1}{\pi} \arccos \frac{v_{\mathrm{e}}}{v_{\mathrm{m}}}\right) $ | (15) |
式中:
经典的模型Archard磨损模型[24-25]如式(16)所示,由该式可知,模具磨损主要与模具表面和工件的接触压力以及二者之间的相对滑动速度成正比,与模具本身的硬度成反比。
| $ W=\int K \frac{p^a v^b}{H^c} \mathrm{~d} t $ | (16) |
式中:
综上分析,为提高冷镦反挤压成形件的成形质量,对模具主要结构进行优化设计。Deform反挤压道次初始状态建模仿真如图 11所示。

|
图 11 大长径比零件反挤压有限元模型 Fig.11 Finite element modeling of reverse extrusion of large aspect ratio parts |
根据反挤压成形中坯料的流动情况,可将其分区进行研究,见图 12,其中Ⅰ区材料受力情况与镦粗类似,材料受到凸模挤压,向一个方向流动,阻碍材料流动的应力大小决定了模具的磨损的大小;Ⅱ区材料流动方向开始转变为反向流动,挤压成形薄壁套管;Ⅲ区材料流动方向为由下转上,这是因为凹模与顶杆阻碍了材料向下流动,使得材料只能沿最小阻碍向上流动,此区域材料的流动情况影响凹模的磨损。
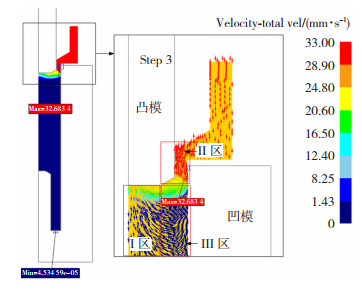
|
图 12 大长径比零件反挤压分区示意图 Fig.12 Schematic diagram of reverse extrusion partition of large aspect ratio parts |
如图 13所示,凸模最大应力出现在模具顶端,最大应力为233.585 MPa,凹模中应力集中位置在反挤压凹模出口处,最大应力为427.924 MPa,应力集中处对应图 12中的Ⅲ区。
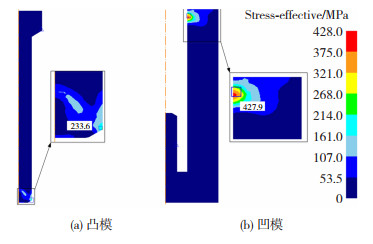
|
图 13 振动辅助反挤压成形模具应力图 Fig.13 Die stress diagram for vibration-assisted reverse extrusion: (a)punch; (b)die |
针对模具应力集中的现象,可以对模具形状进行优化,由于凹模有成形的要求,形状不能改变,因此针对不同凸模结构进行对比分析,具体见图 14,其中:a方案凸模采用直角,b方案将凸模设计为30°倒角,c方案将凸模设计为R2.5圆角,d方案是在b方案的基础上,将凸模增加一级倒角,采用2级倒角。
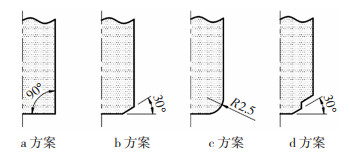
|
图 14 反挤压成形模具几何优化示意图 Fig.14 Schematic diagram of geometric optimization of vibration-assisted reverse extrusion die |
模具优化的直接目的是促进金属的流动,从而减小模具的应力集中,同时坯料内部的应力也得到相应减小。在成形过程中,零件内部的成形应力在反挤压起始阶段快速上升,在挤压行程为0.2 mm时,流动应力达到接近最大值1 280 MPa。图 15为不同凸模结构在行程为0.2 mm时的坯料成形应力分布图。在此行程下,分别在a、b,c,d的4个方案中取最大流动应力,其最大应力分别为1 245.93、1 237.86、1 238.98和1 235.9 MPa。方案a、b和c中最大应力均出现在镦粗部分,挤出部分受力较小。
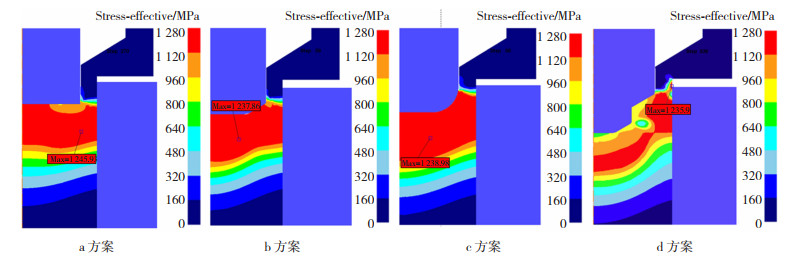
|
图 15 不同凸模设计方案冷镦成形坯料应力云图 Fig.15 Stress cloud diagram of blank formed by cold heading with different punch designs |
将a方案分别与b、c、d方案对比可知:b方案最大应力降低了8.07 MPa,c方案最大应力降低了6.95 MPa,d方案最大应力降低了10.03 MPa。采用二级倒角结构的d方案所受最大应力最小,能够更有效的促进工件的流动,缓解镦粗部分的应力集中现象,使成形质量得到提升。
图 16和图 17是本文对一级倒角和二级倒角进行的模具磨损仿真分析。结合图 12的材料流动分析,Ⅲ区的材料流动使得凹模受到横向的挤压力,模具的磨损较大,在经过二级倒角分散流动压力后,可以看到模具损耗降低,而凸模的磨损也集中在第一级倒角的头部。由此,在设计凸模模具时,可以采用不同材料进行镶嵌的方式,第一级区域采用高一级硬度的材料,而第二级区域可以采用硬度相对低一级的材料,以降低模具制造成本。
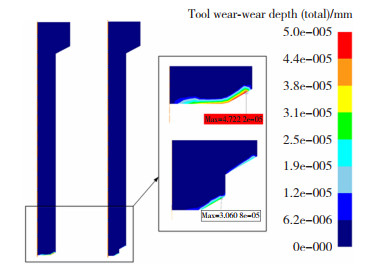
|
图 16 振动辅助反挤压成形模具磨损(凸模) Fig.16 Die wear of vibration-assisted reverse extrusion |
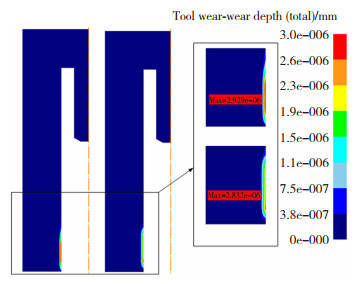
|
图 17 振动辅助反挤压成形模具磨损(凹模) Fig.17 Die wear of vibration-assisted reverse extrusion |
1) 本文以位错密度变化率作为内变量,并在内变量演化过程中,描述了振动的应力叠加效应以及金属变形过程中的材料软化现象,并参考实验数据,采用MATLAB优化算法确定了本构关系模型各个参数。
2) 利用本文建立的本构模型进行了Ti-45Nb材料大长径比薄壁零件冷镦成形仿真,仿真结果表明:施加振动辅助可以有效降低成形载荷及坯料的内部应力,使应力分布更加均匀。
3) 针对较难成形的反挤压薄壁套管道次,在振动辅助冷镦成形工艺的基础上改进模具结构,针对模具应力集中的部位,设计了多种不同类型的倒角过渡方案。结果表明:相较于直角、圆弧倒角和30°倒角,多级倒角能够较好地促进材料的流动,分散模具应力,降低模具损耗。
| [1] |
于福权, 方振龙. 钛合金薄壁件超声振动辅助铣削工艺研究[J]. 机电工程, 2023, 40(1): 129-135. YU Fuquan, FANG Zhenlong. Ultrasonic vibration aided milling technology of titanium alloy thin-walled parts[J]. Journal of Mechanical & Electrical Engineering, 2023, 40(1): 129-135. |
| [2] |
李银标, 刘泰达. 铸造TC4钛合金的组织与性能研究[J]. 热加工工艺, 2022, 51(21): 65-68. LI Yinbiao, LIU Taida. Study on microstructure and properties of casting TC4 titanium alloy[J]. Hot Working Technology, 2022, 51(21): 65-68. |
| [3] |
齐振超, 肖叶鑫, 王星星, 等. Ti45Nb铆钉脉冲电流辅助压铆成形性能分析[J]. 中国机械工程, 2021, 32(23): 2832-2839, 2849. QI Zhenchao, XIAO Yexin, WANG Xingxing, et al. Performance analysis of pulse current assisted press riveting for Ti45Nb rivets[J]. China Mechanical Engineering, 2021, 32(23): 2832-2839, 2849. DOI:10.3969/j.issn.1004-132X.2021.23.007 |
| [4] |
张成浩. 不锈钢精密零件冷镦成形研究[J]. 模具工业, 2021, 47(11): 69-73. ZHANG Chenghao. Research on cold heading forming of precision stainless steel parts[J]. Die & Mould Industry, 2021, 47(11): 69-73. DOI:10.16787/j.cnki.1001-2168.dmi.2021.11.015 |
| [5] |
蒋鹏, 贺小毛, 杨勇, 等. 国内精密塑性成形技术的发展及其在工业生产中的应用[J]. 模具工业, 2020, 46(12): 11-16. JIANG Peng, HE Xiaomao, YANG yong, et al. Development of domestic precision plastic forming technology and its application in industrial production[J]. Die & Mould Industry, 2020, 46(12): 11-16. DOI:10.16787/j.cnki.1001-2168.dmi.2020.12.002 |
| [6] |
杨李杰, 陈兴, 孙宝寿. TC4钛合金管振动辅助成形规律的仿真分析[J]. 热加工工艺, 2023, 52(5): 102-107. YANG Lijie, CHEN Xing, SUN Baoshou. Simul-ation analysis on vibration-assisted forming law of TC4 titanium alloy pipe[J]. Hot Working Technology, 2023, 52(5): 102-107. DOI:10.14158/j.cnki.1001-3814.20210219 |
| [7] |
张海栋, 邓磊, 王新云, 等. 振动辅助塑性成形机理及应用研究进展[J]. 航空制造技术, 2020, 63(16): 22-31. ZHANG Haidong, DENG Lei, WANG Xingyun, et al. Research progress on mechanism and application of vibration assisted plastic forming[J]. Aeronautical Manufacturing Technology, 2020, 63(16): 22-31. DOI:10.16080/j.issn1671-833x.2020.16.022 |
| [8] |
KIRCHNER H, KROMP W K, PRINZ F B, et al. Plastic deformation under simultaneous cyclic and unidirectional loading at low and ultrasonic frequencies[J]. Materials Science and Engineering, 1985, 68(2): 197-206. DOI:10.1016/0025-5416(85)90409-4 |
| [9] |
蔡改贫, 刘峥, 张晖. 低频脉冲振动条件下金属成形的体积效应分析[J]. 锻压技术, 2008, 33(5): 155-159. CAI Gaipin, LIU Zheng, ZHAN Hui. Volume effect analysis of metal deformation with low-frequency pulse vibration[J]. Forging & Stamping Technology, 2008, 33(5): 155-159. |
| [10] |
王家鹏, 赵震, 庄新村, 等. 超声振动辅助成形本构模型[J]. 塑性工程学报, 2015, 22(6): 1-6. WANG Jiapeng, ZHAO Zheng, ZHUANG Xincun, et al. Study on constitutive model of ultrasonic vibration assisted forming[J]. Journal of Plasticity Engineering, 2015, 22(6): 1-6. DOI:10.3969/j.issn.1007-2012.2015.06.001 |
| [11] |
陈晓晓, 徐长续, 成梓楠, 等. 基于改进本构模型的超声辅助渐进成形仿真研究[J]. 锻压技术, 2019, 44(6): 81-87. CHEN Xiaoxiao, XU Changxu, CHENG Zinan, et al. Research on simulation of ultrasonic-assisted incremental forming based on improved constitutive model[J]. Forging & Stamping Technology, 2019, 44(6): 81-87. DOI:10.13330/j.issn.1000-3940.2019.06.012 |
| [12] |
温诗铸. 材料磨损研究的进展与思考[J]. 摩擦学学报, 2008(1): 1-5. WEN Shizhu. Research progress on wear of materials[J]. Tribology, 2008(1): 1-5. DOI:10.16078/j.Tribology.2008.01.002 |
| [13] |
张剑寒, 方刚. 基于有限元模拟和正交实验方法的轴承钢球冷镦工艺及模具优化[J]. 塑性工程学报, 2009, 16(3): 211-217. ZHANG Jianhan, FANG Gang. Optimization for cold heading process and die design of bearing steel ball by finite element simulation and orthogonal test method[J]. Journal of Plasticity Engineering, 2009, 16(3): 211-217. DOI:10.3969/j.issn.1007-2012.2009.03.043 |
| [14] |
丛兵兵, 孔明, 张弘斌, 等. 马车螺栓冷镦成形有限元模拟及模具设计[J]. 塑性工程学报, 2022, 29(2): 76-81. CONG Bingbing, KONG Ming, ZHANG Honbin, et al. Finite element simulation and die design of cold heading forming for carriage bolt[J]. Journal of Plasticity Engineering, 2022, 29(2): 76-81. DOI:10.3969/j.issn.1007-2012.2022.02.011 |
| [15] |
FERNANDES J, ALVES L M, MARTINS P A F. Forming tubular hexahedral screws-process development by means of a combined finite element-boundary element approach[J]. Eng Anal Bound Elem, 2012, 36(7): 1082-1091. DOI:10.1016/j.enganabound.2012.01.007 |
| [16] |
MORAES Costa A L, SILVA U S, VALBERG H S. On the friction conditions in FEM simulations of cold extrusion[J]. Procedia Manufacturing, 2020(47): 231-236. DOI:10.1016/j.promfg.2020.04.202 |
| [17] |
LIN Jun, PRUNCU Catalin, ZHU Lihua, et al. Deformation behavior and microstructure in the low-frequency vibration upsetting of titanium alloy[J]. Journal of Materials Processing Tech, 2022(299): 117360. DOI:10.1016/j.jmatprotec.2021.117360 |
| [18] |
ESTRIN Y. Dislocation theory based constitutive modelling: Foundations and applications[J]. Journal of Materials Processing Technology, 1998(80-81): 33-39. DOI:10.1016/S0924-0136(98)00208-8 |
| [19] |
MECKING H, KOCKS U F. Kinetics of flow and strain-hardening[J]. Acta Metallurgica, 1981, 29(11): 1865-1875. DOI:10.1016/0001-6160(81)90112-7 |
| [20] |
SUN Z C, YANG H, HAN G J, et al. A numerical model based on internal-state-variable method for the microstructure evolution during hot-working process of TA15 titanium alloy[J]. Materials Science & Engineering: A, 2010, 27(15): 3464-3471. DOI:10.1016/j.msea.2010.02.009 |
| [21] |
刘光辉, 刘华, 王涛, 等. 六角抽孔螺栓多工位冷镦成形工艺[J]. 锻压技术, 2020, 45(2): 49-55. LIU Guanghui, LIU Hua, WANG Tao, et al. Multi-station cold upsetting process for six-angle hole bolt[J]. Forging & Stamping Technology, 2020, 45(2): 49-55. DOI:10.13330/j.issn.1000-3940.2020.02.008 |
| [22] |
SUSAN M, BUJOREANU L G. The metal-tool contact friction at the ultrasonic vibration drawing of ball-bearing steel wires[J]. Revista de Metalurgia, 1999, 35(6): 379-384. DOI:10.3989/revmetalm.1999.v35.i6.646 |
| [23] |
温诗铸. 摩擦学原理[M]. 5版. 北京: 清华大学出版社, 2018: 336-337. WEN Shizhu. Principles of tribology[M]. Beijing: Tsinghua University Publishing House, 2018: 336-337. |
| [24] |
桂长林. Archard的磨损设计计算模型及其应用方法[J]. 润滑与密封, 1990(1): 12-21. GUI Changlin. The archard design calculation model and its application methods[J]. Lubrication Engineering, 1990(1): 12-21. |
| [25] |
杨晓俊, 朱兴龙. 基于修正Archard磨损理论非标销轴温镦成形模具磨损研究[J]. 锻压技术, 2021, 46(11): 32-37. YANG Xiaojun, ZHU Xinglong. Study on wear of warm upsetting mold for non-standard pin shaft based on revised archard wear theory[J]. Forging & Stamping Technology, 2021, 46(11): 32-37. DOI:10.13330/j.issn.1000-3940.2021.11.005 |
| [26] |
LEE G A, IM Y T. Finite-element investigation of the wear and elastic deformation of dies in metal forming[J]. Journal of Materials Processing Technology, 1999(89-90): 123-127. DOI:10.1016/S0924-0136(99)00148-X |
| [27] |
皇涛, 宋宇, 张丹丹, 等. 基于修正的Archard磨损理论模型的H13模具钢热挤压磨损研究[J]. 锻压技术, 2019, 44(9): 160-166. HUANG Tao, SONG Yu, ZHANG Dandan. Study on hot extrusion wear of H13 die steel based on modified Archard wear theory model[J]. Forging & Stamping Technology, 2019, 44(9): 160-166. |
 2024, Vol. 32
2024, Vol. 32


