2. 轧制技术及连轧自动化国家重点实验室(东北大学),沈阳 110819;
3. 铜陵学院 工程液压机器人安徽普通高校重点实验室,安徽 铜陵 244061;
4. 燕山大学 国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004
2. State Key Lab of Rolling and Automation (Northeastern University), Shenyang 110819, China;
3. Key Laboratory of Construction Hydraulic Robots of Anhui Higher Education Institutes, Tongling University, Tongling 244061, China;
4. National Engineering Research Center for Equipment and Technology of Cold Rolled Strip, Yanshan University, Qinhuangdao 066004, China
滑移带是指塑性滑移流动集中在很窄的区域,即滑移集中区,滑移累积逐渐从细窄带扩展成粗滑移带,再发展成宏观剪切带或变形带,常见于各类材料的弹-塑性变形[1-3]。滑移集中宏观表现为变形的局部化和各向异性,其显著影响材料的性能和变形行为,如织构演化、变形响应,最明显的就是引起材料表面粗化和降低均匀塑性变形能力,导致材料变形的中断和不稳定。采用实验或数值模拟的方法准确预测材料变形过程中滑移带的萌生和扩展,对调控材料组织性能和变形机制具有重要的指导意义[4-7]。
滑移带或滑移集中是典型的非稳态塑性变形,其主要是由材料微观结构信息和变形条件等引起的软化效应导致的[8-12]。材料变形过程中的软化效应主要有热激活软化和几何软化,极薄带轧制过程属于类准静态变形,其滑移带演化过程忽略轧件温升的影响,极薄带轧制变形中滑移带演化只由几何软化导致。变形过程中,已启动滑移系的滑移面和滑移方向转向易滑移构形,引起晶格的转动,进而产生几何软化效应。几何软化已在各类材料变形模式中被观察到,并被广泛研究,如单轴拉伸、平面应变压缩、纯弯曲、平面剪切和疲劳。Kuroda等[13]研究了典型织构对轧制铝合金薄带单轴拉伸变形中缩颈位置的剪切带分布,S织构时在缩颈处形成与拉伸方向呈45°的剪切带。Luan等[14]采用实验和模拟方法研究了平面应变压缩单/多晶体纯铝的变形带演化,初次和二次滑移带相交阻碍了晶格滑移,促进了晶格转动,进而稳定变形带及其方向。在纯弯曲变形中,晶粒形貌和织构影响剪切带的萌生和扩展路径,在多晶体材料的拉-压面都形成了较为剧烈的剪切带[15]。Li等[16]对铝合金裂纹尖端塑性区域在疲劳载荷作用下的滑移带萌生和演化进行了研究,表明大尺寸和高密度的不可剪切第二相可以抑制滑移带的形成。
晶体塑性有限元方法(CPFEM)被广泛的应用于材料变形的各向异性和局部化研究,其将总变形梯度分解成位错滑移的塑性梯度和晶格转动、畸变的弹性梯度,晶体塑性有限元模型考虑了晶格转动,可以准确获取变形过程的几何软化效应、滑移带演化和位错滑移[17-21]。CPFEM还可准确预测晶粒和亚晶尺度的应变局部化以及变形条件、织构、晶粒形貌等对变形局部化的影响规律,这可能导致滑移带和剪切带的萌生与扩展。模拟滑移带萌生与扩展时,每个变形晶粒被一定数量的单元离散,每个单元只是晶粒的组成部分,如果采用一个单元代表一个晶粒,是不能获取滑移带的演化信息。采用CPFEM模拟多尺度剪切带演化的研究较多,而非稳态的剪切带是由滑移累积的滑移带扩展形成,如能直接预测滑移带的萌生与扩展对调控极薄带材轧制工艺和组织性能具有重要的参考[22-27]。
为优化极薄带轧制工艺,采用晶体塑性有限元方法对拉-压-剪复合应力状态下极薄带轧制滑移带演化进行模拟,建立了极薄带轧制变形的晶体塑性有限元模型,着重分析了轧制区剪切强度和轧制压下率对变形晶粒滑移带萌生与扩展的影响规律。
1 晶体塑性理论本文采用的是晶体塑性理论,该理论由Hill[28]和Asaro[29]进行了完整的描述,将总变形分解成位错在特定滑移系上滑移导致的塑性变形部分和晶格畸变、转动的弹性变形部分。对于面心立方金属,存在12个{111}<110>滑移系,其中{111}为滑移面、<110>为滑移方向,各滑移系的编号如表 1所示。
| 表 1 滑移系的标定 Table 1 The slip system considered in present study |
总变形梯度F分解成弹性变形梯度Fe和塑性变形梯度Fp
| $ \boldsymbol{F}=\boldsymbol{F}^\mathrm{e} \cdot \boldsymbol{F}^{\mathrm{p}} $ | (1) |
式中Fp为沿晶体滑移平面产生的非弹性剪切变形,其变形率可表示为
| $ \dot{\boldsymbol{F}}^{\mathrm{p}}=\boldsymbol{L}^{\mathrm{p}} \cdot \boldsymbol{F}^{\mathrm{p}} $ | (2) |
式中Lp为塑性速度梯度,可表示为所有启动滑移系的剪切应变速率
| $ \boldsymbol{L}^{\mathrm{p}}=\sum\limits_\alpha \dot{\gamma}^\alpha \operatorname{sign}\left(\tau^\alpha\right) \boldsymbol{S}^\alpha, \dot{\gamma}^\alpha>0 $ | (3) |
式中:Sα为施密特因子,Sα=mα×nα;mα为滑移方向的向量;nα为滑移面法向的向量; τα为滑移系α上的分切应力。
率相关单晶体塑性理论的弹性本构方程为
| $ \overline{\boldsymbol{\sigma}}^{\mathrm{e}}=\boldsymbol{C}: \boldsymbol{D}^{\mathrm{e}} $ | (4) |
式中:C为弹性模量张量;De为变形率弹性部分;σe为Kitchhoff应力的Jaumann应力率弹性部分。
| $ \overline{\boldsymbol{\sigma}}^\mathrm{e}=\dot{\boldsymbol{\sigma}}-\boldsymbol{W}^\mathrm{e} \boldsymbol{\sigma}+\boldsymbol{\sigma} W^\mathrm{e} $ | (5) |
式中We为旋转率张量的弹性部分。
启动滑移系α上的滑移率
| $ \dot{\gamma}^\alpha=\dot{\gamma}_0^\alpha\left(\frac{\tau^\alpha}{g^\alpha}\right)^n $ | (6) |
| $ \boldsymbol{\tau}^\alpha=\left(\boldsymbol{F}^{\mathrm{e} \mathrm{~T}} \cdot \boldsymbol{F}^\mathrm{e} \cdot \boldsymbol{T}\right): \boldsymbol{S}^\alpha $ | (7) |
式中:
gα率的增加,即滑移硬化模型为
| $ \dot{g}^\alpha=\sum h_{\alpha \mathtt{β}} \dot{\gamma}^\mathtt{β} $ | (8) |
式中hαβ为硬化系数,其中hαα和hαβ(α≠β)分别为自硬化和潜硬化系数。
采用Bassani和Wu[30]提出的符合面心立方金属单晶体3个滑移过程的硬化规律来描述自硬化系数
| $ h_{\alpha \alpha}=h_0 \operatorname{sech}^2\left[\frac{h_0 \gamma}{\tau_\text{s}-\tau_0}\right] $ | (9) |
式中:h0为初始硬化率;τ0为每个启动滑移系都相同的初始临界分剪切力;τs为临界分剪切力饱和值;γ为所有启动滑移系的累积切应变
| $ \gamma=\sum\limits_\alpha \int_0^t\left|\dot{\gamma}^\alpha\right| \mathrm{d} t $ | (10) |
潜硬化系数表示为
| $ h_{\alpha \mathtt{β}}=q h_{\alpha \alpha} $ | (11) |
式中q为潜硬化系数与自硬化系数的比值,本研究取q=1.0。
将上述单晶体的晶体塑性本构通过有限元软件Abaqus的用户子程序UMAT开发,实现滑移带演化的晶体塑性有限元模拟分析。
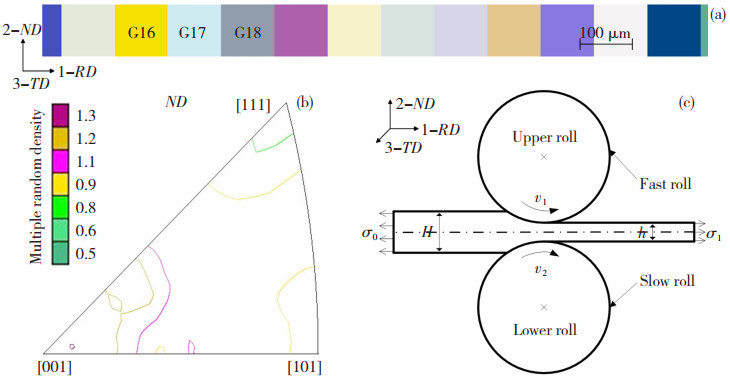
2 晶体塑性有限元建模与方法为探究极薄带轧制滑移带的演化规律以及减少晶界和取向对其变形行为的影响,在建立极薄带轧制模型时,其厚度上只分布一层晶粒,即单层晶组织,如图 1(a)所示,各晶粒(如图中的G16、G17、G18)的晶界与轧制方向垂直,平均晶粒直径d=100 μm,与极薄带厚度t相同,t/d=1。前期轧制极薄带退火实验结果表明,100 μm厚铜箔经完全真空退火后沿其厚度的反极图如图 1(b)所示,表明无特定织构,晶粒呈随机取向分布。因此对所建的单层晶组织赋予随机晶粒取向,用颜色的不同来区分各晶粒的取向分布,相邻晶粒取向差大于15°。极薄带轧制如图 1(c)所示,通过改变上下轧辊的转速,可在轧制区施加不同程度的剪切变形,再在极薄带前后施加相应张应力,则在轧制区形成拉拔-压缩-剪切的复合应力状态,进一步提高轧机的薄轧能力。晶体塑性有限元模拟极薄带轧制变形的轧制工艺为:前后张应力σ1=σ0=100 MPa,轧制压下率为20%~80%,上工作辊转速为1.04 rad/s,上下轧辊异速比为1.0~1.5,上工作辊为快速辊,下工作辊为慢速辊,轧件与轧辊之间采用库伦摩擦,摩擦系数为0.1。
|
图 1 赋予随机取向的极薄带晶体塑性有限元模型(a), 退火后沿铜箔厚度方向织构分布(b)及极薄带轧制示意图(c) Fig.1 (a) Show the CPFEM model of foil rolling bamboo crystal colored according to the inverse pole figure along normal direction, (b) show the initial texture in standard triangle along normal direction of the experimental bamboo crystal pure copper foil with thickness t=100 μm and (c) show the boundary condition and schematic illustration of foil rolling process |
有限元分析用到的材料性能和滑移硬化参数如表 2所示,每个启动滑移系的初始硬化参数都是一样的,这些参数是通过拟合沿轧制方向制取厚度100 μm铜箔拉伸试样的拉伸实验曲线与对应晶体塑性有限元模拟曲线而来[25, 31-32]。
3 结果与分析 3.1 剪切演化所建极薄带轧制模型,其厚度方向只分布一层晶粒组织,既考虑了相邻晶粒之间晶界的作用又降低了三角晶界变形的复杂程度,以下着重对轧制变形区接触弧长内3个相邻晶粒的微观变形进行分析。
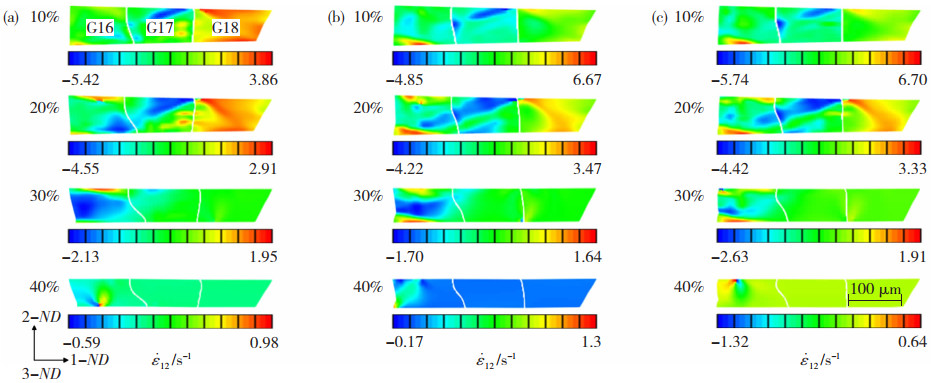
图 2显示了40%压下率时轧制区3个相邻晶粒在不同异速比的动态剪切带演化过程,表明单层晶极薄带轧制变形为显著的局部剪切,在各变形晶粒内形成了不同程度的剪切变形集中区域,即宽度和方向分布不同的剪切带,晶粒G16内形成与轧制方向平行的且宽度最大达到80 μm的剪切带,晶粒G17和G18内形成了关于晶界对称分布的集中剪切带。对于极薄带轧制在其变形区施加拉拔-压缩-剪切复合应力状态可促进晶粒的剪切变形,即在变形晶粒内部形成新的剪切带,而已有剪切带则更加集中。相同工艺条件下,同步轧制时各变形晶粒内剪切带的宽度大于异步轧制。异步轧制可增强剪切变形,通过形成新剪切带和多剪切带实现,但是随着轧制区剪切变形的增强,晶粒变形的局部化更加明显,宽的剪切带逐步分解成更加细小的剪切带,在晶界处形成剪切集中,晶界协调变形的能力增强。
|
图 2 不同异速比时剪切应变速率在轧制变形区晶粒内的演化 Fig.2 Evolution of shear strain rate in grain of rolling deformation zone with different asymmetric speed ratios: (a) 1.0; (b) 1.1; (c) 1.3 |
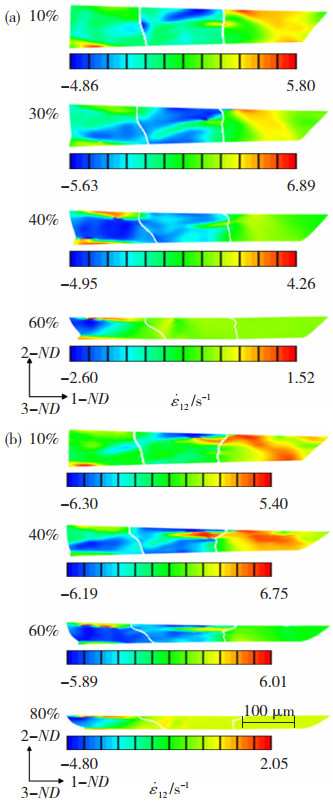
为进一步提高极薄带轧机的轧薄能力,在施加前后张应力和压下的同时,在轧制区再施加恰当剪切变形可增强极薄带的剪切变形,改善变形区的应力状态,实现轧件的极限减薄。图 3显示了异速比1.1时轧制区3个相邻晶粒在不同压下率的动态剪切带演化过程,40%压下率的演化过程可见图 2(b),表现为明显的局部剪切,随轧制压下率的增加,各变形晶粒的剪切带逐渐扩展变宽,晶内剪切区域扩大,如当轧制压下率达到80%(图 3(c))时,在变形晶粒内除已有剪切带发生扩展外,还出现了方向相反的剪切集中区域,但已形成的剪切带只发生扩展变宽,剪切带的方向没有发生变化。在极薄带轧制区施加前后张应力和剪切外,如再施加大的压下率,可促进已变形晶粒发生更加显著的剪切变形,通过已有剪切带的扩展和产生新剪切带来实现。在轧制区已有拉拔-剪切应力状态下再施加大的压下率时,晶界处形成剪切集中,甚至出现方向相反的剪切带,晶界处变形较为剧烈,尤其靠近晶界的上下区域,这样不利于箔轧过程稳定进行。
|
图 3 不同压下率时剪切应变速率在轧制变形区晶粒内的演化 Fig.3 Evolution of shear strain rate in grain of rolling deformation zone with different rolling reductions: (a) 60%; (b) 80% |
变形晶粒内的剪切带演化过程表明,在轧制区的张应力和压下率一定时,再施加额外剪切应力,促进变形晶粒内剪切带的新形成和更加缩窄集中,剪切变形增强,晶界协调变形能力增强;在轧制区的张应力和剪切一定时,再施加恰当的压下率时,变形晶粒内部已有剪切带发生扩展变宽以及形成新的剪切带。但是较强的剪切强度和较大轧制压下,会造成晶界处变形剧烈以及在轧制极薄带表面产生缺陷,导致断带和轧制终止。在轧制区引入拉拔-压缩-剪切复合应力,单层晶极薄带轧制变形时剪切较为平稳和强烈,有利于极薄带的进一步轧制减薄。
3.2 单滑移演化剪切带的形成是由于相邻晶粒协调变形而发生转动,引起已启动滑移系转向易滑移方向,滑移集中区域扩展到一定程度,由介观粗滑移带演变成宏观剪切带。轧制铜极薄带变形中可能启动的滑移系共有12个,即{111} <110>,分为a、b、c和d 4组,详见陈守东等[25, 31-32]工作。特选取c组c1滑移系在异步轧制单层晶极薄带变形中的滑移演化,以分析单滑移规律。
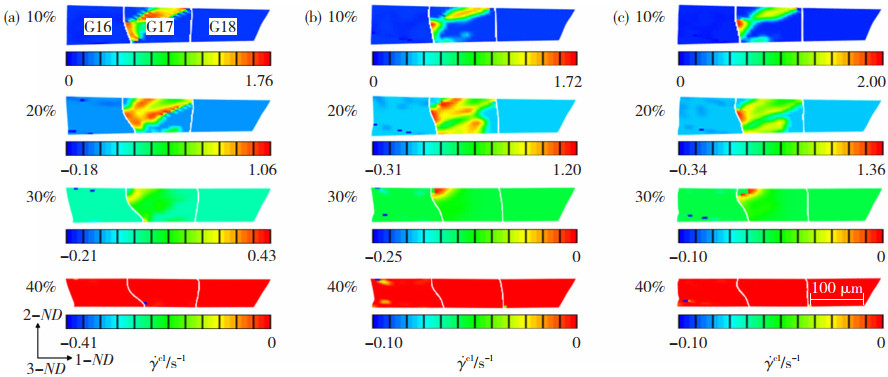
图 4显示了40%压下率和不同异速比时滑移系c1在轧制区3个相邻晶粒内-间的动态滑移演化过程,c1只在晶粒G17中被激活滑移,在晶粒G16中进行微弱滑移。同步轧制时,c1在晶粒内形成与轧制方向呈45°的集中滑移带,随轧制变形的进行,主滑移带逐步分解成系列窄滑移带且方向不变;异步轧制时,除主滑移带分解成细小窄滑移带以外,还形成了与主滑移带方向一致的次滑移带,随轧制区剪切变形的增强,主次滑移带都更加集中,晶界处滑移集中更加显著。
|
图 4 滑移系c1在不同轧制异速比时的滑移演化 Fig.4 The slip evolution of c1 at different rolling asymmetric speed ratios: (a) 1.0; (b) 1.1; (c) 1.3 |
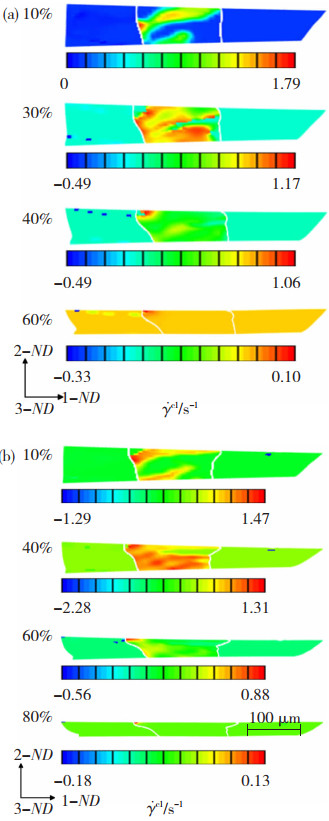
图 5显示了异速比1.1和不同压下率时滑移系c1在轧制区3个相邻晶粒内-间的动态滑移演化过程,40%压下率的演化过程可见图 4(b),同样表现出增大压下率并不能激活当前未在变形晶粒内滑移的滑移系而进行新的滑移运动,已启动滑移系的滑移强度和滑移区域随轧制压下率的增加而增大,增大压下率,促使主次滑移带向彼此相互扩展,但当轧制压下率很大时,滑移带出现缩窄和更加集中,且晶界处滑移更加剧烈。
|
图 5 滑移系c1在不同轧制压下率时的滑移演化 Fig.5 The slip evolution of c1 at different rolling reductions: (a) 60% and (b) 80% |
有两点值得注意,一是虽然只列举了12个滑移系中1个启动滑移系的滑移过程,但这个典型滑移系的单滑移演化过程与相同工艺条件下的剪切变形演化具有一定的关系,且也具有独特性,如最明显的是滑移系c1在晶粒G17中的滑移演化与晶粒G17的剪切演化更具一致性,即晶粒G17中形成的主次剪切带与c1在其中形成的主次滑移带一一对应,表明滑移系c1的滑移主导晶粒G17的剪切变形,充分再现和验证了多晶体塑性变形主次滑移和主次变形晶粒的机制,也揭示出单层晶极薄带轧制变形机制;二是单系滑移形成的主次滑移带中存在明显的滑移梯度以及滑移带分解,这完全有别于宏观的剪切带分布及演化规律,这表明所建立的晶体塑性有限元模型可以准确获取单层晶极薄带轧制变形介观层次的变形特性信息,可为分析和掌握箔轧工艺和极薄带组织结构对其轧制变形机制的影响规律提供必要的理论参考。
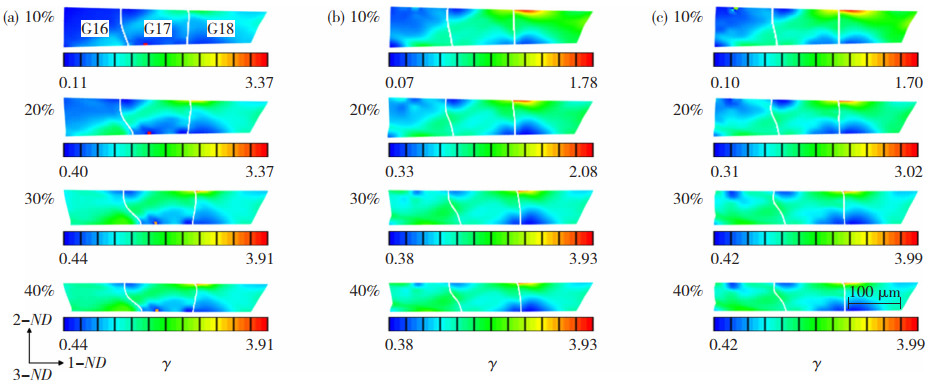
3.3 累积滑移演化单滑移系反映出单层晶极薄带轧制变形的特殊物理机制,即滑移局部化和强晶界协调性。变形过程中可被激活参与滑移运动的滑移系共有12个,单个滑移系的滑移演化具有一定的特定性,不能反映变形的整个过程,图 6显示了40%压下率和不同异速比时12个启动滑移系在轧制区3个相邻晶粒内-间的累积滑移过程。无论同步轧制还是异步轧制,即使单个晶粒具有同样的晶体取向,但是在单个变形晶粒内都存在易滑移区域和难变形区域,单层晶结构表现出很强的变形协调作用,形成了贯穿晶粒和晶界的集中累积滑移带。在轧制变形区施加剪切时,变形晶粒内的累积滑移区域扩大,在局部形成了强滑移区。同步轧制时的难变形区域也进行了相应的滑移运动,晶粒的滑移区域增大且更加均匀,形成贯穿晶界的累积滑移带,且该累积滑移带在晶界两侧的宽度一样,表明晶界协调滑移作用更加显著,晶界承载了很好的滑移传递作用。但是随着变形区剪切作用的加强,累积滑移表现出与单个滑移系滑移演化相似的规律,即累积滑移带宽度缩窄,强滑移程度进一步增大,晶粒内部的难变形区并没有缩小,贯穿晶界两侧的累积滑移带的宽度也减小,晶界处滑移集中强度大,轧制极薄带表层表现出较强的难-易滑移区域的交替变换现象。
|
图 6 不同异速比时累积滑移在轧制变形区晶粒内的演化 Fig.6 Evolution of accumulated slip in grain of rolling deformation zone with different asymmetric speed ratios: (a) 1.0; (b) 1.1; (c) 1.3 |
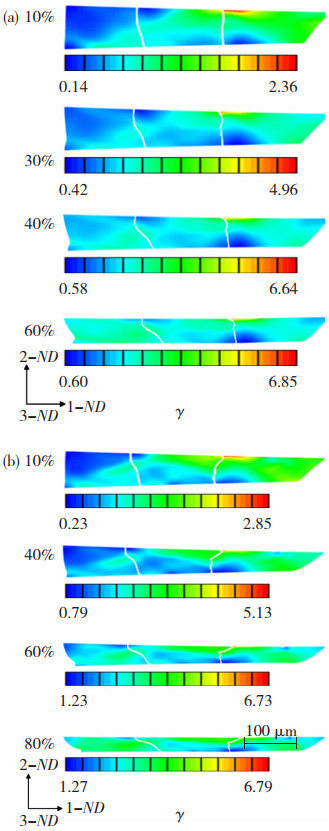
在极薄带轧制区施加恰当的剪切变形,可促进滑移运动和降低一定程度的变形局域化,图 7显示了异速比1.1和不同压下率时12个滑移系在轧制区3个相邻晶粒内-间的累积滑移过程,40%压下率的演化过程可见6(b),在轧制区已有拉-剪应力状态下再施加较大压应力时,原来的难滑移区仍然没有因为增大压下率而进行滑移,但从最终轧制结果可见,采用较大压下率轧制相当于减小了难变形区占整个变形晶粒的面积比例。随轧制压下率的增大,轧制变形过程中累积滑移更加集中和局部化,贯穿晶界的累积滑移带发生缩颈、断带和缩窄。当轧制压下率很大时,只在晶界两侧形成了滑移集中,晶界处变形较为剧烈,晶界发生弯折,轧制过程可能失稳。
|
图 7 不同压下率时累积滑移在轧制变形区晶粒内的演化 Fig.7 Evolution of accumulated slip in grain of rolling deformation zone with different rolling reductions: (a) 60%; (b) 80% |
极薄带轧制各变形晶粒的累积滑移过程与其剪切变形和单滑移演化具有很好的一致性,都表明在极薄带轧制变形区施加恰当的拉-压-剪复合应力,可促进晶粒滑移和协调变形,晶粒内部滑移区域扩展,滑移均匀性增强。滑移带扩展形成宏观的剪切带,宏观的剪切变形行为反映出了极薄带轧制变形的微观机制。单层晶极薄带具有独特的晶粒组织结构,晶界在左右两晶粒间起到了很好的滑移转移和变形协调作用。
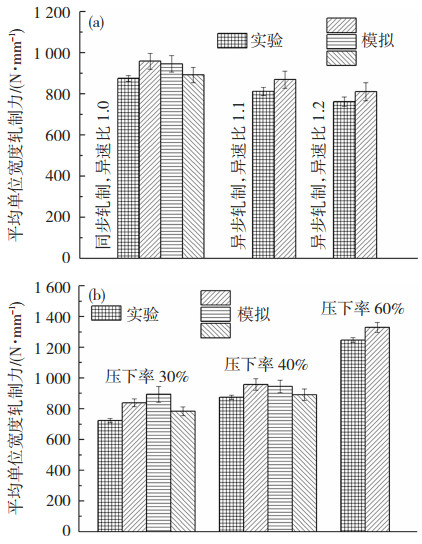
3.4 箔轧实验与验证采用晶体塑性有限元模拟了单层晶极薄带轧制变形的微观机制,揭示了轧制区剪切变形和轧制压下率对其微观变形机制的影响规律。为验证晶体塑性有限元模拟极薄带轧制变形结果的准确性,将不同异速比和轧制压下率的单层晶箔轧实验检测轧制力与对应晶体塑性有限元模拟进行对比。采用自主设计制造的四辊异步微型轧机开展单层晶铜箔的轧制实验,该轧机工作辊直径为30 mm,辊身长度为130 mm;支撑辊直径120 mm,辊身长度120 mm;采用压下螺丝下方的测力传感器测量轧制力,轧制力参数由数据处理器采集,箔轧工艺和晶体塑性有限元模拟一样。将6 mm厚铜板通过二辊同步轧机轧制减薄至0.5 mm,无中间退火,再经四辊异步微型轧机轧薄至100 μm,将长度100 mm×宽度20 mm×厚度0.1 mm的铜箔置于真空炉进行退火处理,退火温度920 ℃,保温7 h,获得的单层晶铜极薄带显微组织如图 8所示,厚度方向只分布一层晶粒组织。图 9(a)显示了40%压下率、同步和异步轧制时的轧制力对比结果,其中晶体塑性有限元模拟极薄带同步轧制时设置了3种晶体取向分布。由图 9(a)可知,异步轧制显著降低轧制力,且轧制力波动程度随异速比的增大而增大,晶体塑性有限元模拟轧制力略高于箔轧实验的检测结果,同时晶体取向分布对极薄带轧制宏观变形的影响较小,尤其同步轧制时的轧制力对晶粒取向的依赖性较小,这与在轧制区施加剪切变形后变形晶粒内部剪切带和滑移带演化规律一致。图 9(b)显示了异速比1.1、不同轧制压下率时的轧制力对比结果,其中30%和40%压下的晶体塑性有限元模拟赋予了极薄带3种取向分布,随轧制压下率的增大,箔轧实验和模拟轧制力都增大,仍然表现出模拟结果略高于实验结果;异步轧制时,虽然压下率改变,但极薄带轧制宏观变形对晶体取向分布的依赖性仍然较小,这与增大轧制压下率并不能激活未启动滑移系进行滑移运动和扩展已启动滑移系的滑移区域的趋势是保持一致的。宏观的箔轧实验结果再现了其微观的变形特性,晶体塑性有限元模拟与实验结果吻合较好,表明晶体塑性有限元可以准确模拟极薄带轧制宏微观变形。

|
图 8 箔轧单层晶铜极薄带轧件显微组织 Fig.8 Microstructure of single layer crystal copper ultra-thin strip in foil rolling |
|
图 9 不同异速比(a)和压下率(b)时极薄带轧制的晶体塑性有限元模拟和实验单位宽度轧制力对比 Fig.9 Comparison of simulated and experimental mean per unit width roll force in foil rolling at different asymmetric speed ratios (a) and different rolling reductions (b) |
1) 在一定拉-压应力状态下,同时在单层晶极薄带轧制区施加额外剪切变形可增强轧制区的剪切变形程度,在已变形晶粒内形成新的剪切带,且随剪切强度的增强,主次剪切带都发生缩窄,变形局部化趋势加剧。在已有拉-剪应力状态下,增大轧制压下率并不能使未变形区产生剪切变形,但可激发已形成的主次剪切带发生扩展,增大剪切区域,同时晶界处的剪切变形更加剧烈。
2) 单滑移系在各变形晶粒内的滑移规律及演化差异很大,在变形晶粒内存在主-次滑移系,在轧制区施加剪切变形可触发主滑移带逐渐分解形成新的细窄次滑移带。在已有拉-剪应力状态下,单层晶铜箔变形晶粒内的单滑移区域随轧制压下率的增大而扩展,但是增大压下率并不能激活该滑移系在未滑移区域进行滑移运动,较大压下率会导致晶界滑移剧烈变化。变形晶粒内形成的单滑移带较剪切带表现出更大非均匀和梯度化,即在宽的滑移带中又存在更为集中的细窄亚滑移带,单滑移带与剪切带具有很好的一致性。
3) 在拉-压-剪复合应力状态下,形成贯穿单层晶铜箔相邻晶粒晶界的累积滑移带,晶界起到了很好的承载和转移滑移的作用。在强剪切和大压下率条件下,累积滑移带有缩窄趋势,且滑移均匀性降低。单滑移带扩展和叠加形成累积滑移带,累积滑移带继续扩展到一定程度形成宏观剪切带,三者具有很好的一致性。
4) 晶体塑性有限元模拟结果与实验测试轧制力结果吻合较好,验证了晶体塑性有限元模拟极薄带轧制变形行为的准确性,单层晶极薄带轧制变形对晶体取向分布的依赖性较小,同时实验和模拟宏观轧制力的波动性与单层晶极薄带轧制微观滑移演化规律是准确对应的。
| [1] |
INOUE J, SADEGHI A, KOSEKI T. Slip band formation at free surface of lath martensite in low carbon steel[J]. Acta Materialia, 2019, 165: 129-141. DOI:10.1016/j.actamat.2018.11.026 |
| [2] |
LIU C, RODDATIS V, KENESEI P, et al. Shear-band thickness and shear-band cavities in a Zr-based metallic glass[J]. Acta Materialia, 2017, 140: 206-216. DOI:10.1016/j.actamat.2017.08.032 |
| [3] |
SUN J L, TRIMBY P W, YAN F K, et al. Shear banding in commercial pure titanium deformed by dynamic compression[J]. Acta Materialia, 2014, 79: 47-58. DOI:10.1016/j.actamat.2014.07.011 |
| [4] |
WAGNER P, ENGLER O, LVCKE K. Formation of Cu-type shear bands and their influence on deformation and texture of rolled f.c.c.{112} 111 single crystals[J]. Acta Metallurgica et Materialia, 1995, 43: 3799-3812. DOI:10.1016/0956-7151(95)90164-7 |
| [5] |
HAO Z P, CUI R R, FAN Y H. Formation mechanism and characterization of shear band in high-speed cutting Inconel718[J]. The International Journal of Advanced Manufacturing Technology, 2018, 98: 2791-2799. DOI:10.1007/s00170-018-2435-6 |
| [6] |
KHAN A S, MEREDITH C S. Thermo-mechanical response of Al6061 with and without equal channel angular pressing (ECAP)[J]. International Journal of Plasticity, 2010, 26: 189-203. DOI:10.1016/j.ijplas.2009.07.002 |
| [7] |
TVERGAARD V. Study of localization in a void-sheet under stress states near pure shear[J]. International Journal of Solids and Structures, 2015, 75 -76: 134-142. DOI:10.1016/j.ijsolstr.2015.08.008 |
| [8] |
ANAND L, ASLAN O, CHESTER S A. A large- deformation gradient theory for elastic-plastic materials: Strain softening and regularization of shear bands[J]. International Journal of Plasticity, 2012, 30 -31: 116-143. DOI:10.1016/j.ijplas.2011.10.002 |
| [9] |
CERRETA E K, BINGERT J F, GRAY Ⅲ G T, et al. Microstructural examination of quasi-static and dynamic shear in high-purity iron[J]. International Journal of Plasticity, 2013, 40: 23-38. DOI:10.1016/j.ijplas.2012.06.005 |
| [10] |
HAN F B, ROTERS F, RAABE D. Microstructure-based multiscale modeling of large strain plastic deformation by coupling a full-field crystal plasticity-spectral solver with an implicit finite element solver[J]. International Journal of Plasticity, 2020, 125: 97-117. DOI:10.1016/j.ijplas.2019.09.004 |
| [11] |
LYCHAGIN D V, FILIPPOV A V, NOVITSKAIA O S, et al. Friction-induced slip band relief of-Hadfield steel single crystal oriented for multiple slip deformation[J]. Wear, 2017, 374-375: 5-14. DOI:10.1016/j.wear.2016.12.028 |
| [12] |
MARTI N, FAVIER V, GREGORI F, et al. Correlation of the low and high frequency fatigue responses of pure polycrystalline copper with mechanisms of slip band formation[J]. Materials Science and Engineering: A, 2020, 772: 138619. DOI:10.1016/j.msea.2019.138619 |
| [13] |
KURODA M, TVERGAARD V. Effects of texture on shear band formation in plane strain tension/compression and bending[J]. International Journal of Plasticity, 2007, 23(2): 244-272. DOI:10.1016/j.ijplas.2006.03.014 |
| [14] |
LUAN Q M, XING H, ZHANG J, et al. Experimental and crystal plasticity study on deformation bands in single crystal and multi-crystal pure aluminium[J]. Acta Materialia, 2020, 183: 78-92. DOI:10.1016/j.actamat.2019.11.006 |
| [15] |
SAAI A, WESTERMANN I, DUMOULIN S, et al. Crystal plasticity finite element simulations of pure bending of aluminium alloy AA7108[J]. International Journal of Material Forming, 2016, 9(4): 457-469. DOI:10.1007/s12289-015-1233-z |
| [16] |
LI F D, LIU Z Y, WU W T, et al. Slip band formation in plastic deformation zone at crack tip in fatigue stage Ⅱ of 2xxx aluminum alloys[J]. International Journal of Fatigue, 2016, 91(1): 68-78. DOI:10.1016/j.ijfatigue.2016.05.014 |
| [17] |
INAL K, WU P D, NEALE K W. Finite element analysis of localization in FCC polycrystalline sheets under plane stress tension[J]. International Journal of Solids and Structures, 2002, 39: 3469-3486. DOI:10.1016/s0020-7683(02)00162-2 |
| [18] |
INAL K, WU P D, NEALE K W. Instability and localized deformation in polycrystalline solids under plane-strain tension[J]. International Journal of Solids and Structures, 2002, 39: 983-1002. DOI:10.1016/s0020-7683(01)00246-3 |
| [19] |
SABNIS P A, MAZIERE M, FOREST S, et al. Effect of secondary orientation on notch-tip plasticity in superalloy single crystals[J]. International Journal of Plasticity, 2012, 28: 102-123. DOI:10.1016/j.ijplas.2011.06.003 |
| [20] |
KESHAVARZ S, GHOSH S. Hierarchical crystal plasticity FE model for nickel-based superalloys: Sub-grain microstructures to polycrystalline aggregates[J]. International Journal of Solids and Structures, 2015, 55: 17-31. DOI:10.1016/j.ijsolstr.2014.03.037 |
| [21] |
郑黎, 张士宏, 何维均, 等. 晶体塑性模型描述多晶体循环加载中的Bauschinger效应[J]. 材料科学与工艺, 2014, 22(6): 78-84. ZHENG Li, ZHANG Shihong, HE Weijun, et al. Description of Bauschinger effect of polycrystalline during cyclic loading by crystal plasticity model[J]. Materials Science and Technology, 2014, 22(6): 78-84. DOI:10.11951/j.issn.1005-0299.20140614 |
| [22] |
SHI R, NIE Z H, FAN Q B, et al. Elastic plastic deformation of TC6 titanium alloy analyzed by in-situ synchrotron based X-ray diffraction and microstructure based finite element modeling[J]. Journal of Alloys and Compounds, 2016, 688: 787-795. DOI:10.1016/j.jallcom.2016.07.105 |
| [23] |
WU H B, TO S. Serrated chip formation and their adiabatic analysis by using the constitutive model of titanium alloy in high speed cutting[J]. Journal of Alloys and Compounds, 2015, 629: 368-373. DOI:10.1016/j.jallcom.2014.12.230 |
| [24] |
YANG G N, SUN B A, CHEN S Q, et al. The multiple shear bands and plasticity in metallic glasses: A possible origin from stress redistribution[J]. Journal of Alloys and Compounds, 2017, 695: 3457-3466. DOI:10.1016/j.jallcom.2016.12.012 |
| [25] |
CHEN S D, LIU X H, LIU L Z. Effects of grain size and heterogeneity on the mechanical behavior of foil rolling[J]. International Journal of Mechanical Sciences, 2015, 100: 226-236. DOI:10.1016/j.ijmecsci.2015.07.003 |
| [26] |
LIM H, CARROLL J D, BATTAILE C C, et al. Grain-scale experimental validation of crystal plasticity finite element simulations of tantalum oligocrystals[J]. International Journal of Plasticity, 2014, 60: 1-18. DOI:10.1016/j.ijplas.2014.05.004 |
| [27] |
IADICOLA M A, HU L, ROLLETT A D, et al. Crystal plasticity analysis of constitutive behavior of 5754 aluminum sheet deformed along bi-linear strain paths[J]. International Journal of Solids and Structures, 2012, 49: 3507-3516. DOI:10.1016/j.ijsolstr.2012.03.015 |
| [28] |
HILL R, RICE J R. Constitutive analysis of elastic-plastic crystals at arbitrary strain[J]. Journal of the Mechanics and Physics of Solids, 1972, 20: 401-413. DOI:10.1016/0022-5096(72)90017-8 |
| [29] |
ASARO R J, NEEDLEMAN A. Overview no.42 texture development and strain hardening in rate dependent polycrystals[J]. Acta Metallurgica, 1985, 33(6): 923-953. DOI:10.1016/0001-6160(85)90188-9 |
| [30] |
BASSANI J L, WU T Y. Latent hardening in single crystals Ⅱ. Analytical characterization and predictions[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1991, 435(1893): 21-41. DOI:10.1098/rspa.1991.0128 |
| [31] |
陈守东, 卢日环, 孙建, 等. 轧制单层和少层晶铜箔塑性各向异性的晶体塑性有限元模拟[J]. 中国有色金属学报, 2021, 31(2): 353-363. CHEN Shoudong, LU Rihuan, SUN Jian, et al. Crystal plasticity finite element simulations for plastic anisotropy in single layer and oligo-crystal copper under foil rolling[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(2): 353-363. DOI:10.11817/j.ysxb.1004.0609.2021-36540 |
| [32] |
陈守东, 陈敬琪, 李杰, 等. 复合成形轧制铜极薄带变形局部化的晶体塑性有限元模拟[J]. 材料导报, 2023, 37(2): 180-189. CHEN Shoudong, CHEN Jingqi, LI Jie, et al. Prediction of deformation localization of copper foil compound forming rolling using crystal plasticity finite element simulations[J]. Materials Reports, 2023, 37(2): 180-189. DOI:10.11896/cldb.21050240 |
 2024, Vol. 32
2024, Vol. 32


