铝粉具有高的热值和反应活性,常作为含能材料中的高能添加剂。含高热值铝粉的含能材料被广泛应用于目标毁伤、推进剂以及其他烟火药剂领域,它能够提高能量、爆热以及增加其反应时间等[1-6],但铝粉在燃烧过程中易发生团聚,这会对铝粉的燃烧效率产生影响[7]。利用球磨工艺将铝(Al)/聚四氟乙烯(PTFE)制备成机械活化含能材料可以有效地解决团聚问题[8]。
行星式球磨机适合于硬脆性材料的细磨乃至纳米材料的超细磨[9],由于离心力场的影响,相对于普通球磨机,行星式球磨机能够获得更大的应力强度。该球磨工艺大多为湿法球磨,在实际的实验中,对于粉体的塑性变形过程无法准确捕捉。而仿真对于磨球与粉体在不同时间下的状态变化的分析则有很大的优势,离散元法能够使颗粒的运动以及变形得到准确的描述,并且可以将颗粒的能量分布、运动变化等准确的记录下来[10]。针对湿法球磨,可以采用流体力学-离散元(Computational Fluid Dynamics-Discrete Element Method,CFD-DEM)耦合方法来模拟液体环境[11]。
由于铝粉的尺寸为微米级,将其与磨球罐以及磨球放在同一尺度下进行仿真,这将使仿真难以运行并计算。为了解决跨度大的问题,Beinert等[12-13]开发了一种多尺度建模方法。通过构建磨球与粉体的仿真模型,分析在磨球相对速度法向与切向分量比值不同的情况下,磨球发生碰撞时,碰撞区域粉体分布的变化,从而得到粉体的应力概率。该多尺度仿真的思想对于微米级铝粉形变的分析模型的建立具有良好的指导意义。
陶俊等[14]对于Al/PTFE的研究指出,球磨后的Al/PTFE只发生其微观物理结构的变化,由于Al与PTFE之间存在巨大的延展性差异,球磨后的铝粉表面被PTFE包裹, 且Al/PTFE的形状主要取决于变形后铝粉的形状,因此仿真仅对铝粉进行建模和分析。本文采用多尺度建模仿真的方法,研究微米级铝粉在球磨的过程中破碎前的形变过程以及在不同状态下的粉体数量,然后进行球磨实验,观测粉体的形态变化,分析粉体破碎后的粒径变化,结合仿真与实验的形变过程,实现对球磨任意时间后的颗粒粒径的预测。
1 多尺度仿真 1.1 实验材料与参数球磨罐体材质为氧化锆(ZrO2),容积为100 mL,工作容积为30 mL,内径为52 mm,内高为50 mm,公转半径为85 mm。磨球的直径为3 mm,其材质为氧化锆,氧化锆的参数如表 1所示。磨球的总质量为180 g,球料比为5 ∶1,Al与PTFE的质量比为6 ∶4,粒径皆为5 μm,研磨液体为40 mL的无水乙醇。
| 表 1 氧化锆参数 Table 1 Parameters of ZrO2 |
多尺度仿真是将整个仿真体系划分为宏观、介观、微观的组合进行仿真。
宏观尺度,采用EDEM软件建立磨球与球磨罐体模型,为了准确研究磨球之间相互碰撞过程中影响球磨效率的主要因素,通过CFD-DEM耦合的方式对实际的液体环境进行仿真[15]。在宏观仿真中,首先磨球的相对速度分布,再通过相对速度分布建立介观尺度模型并确定应力能量分布。
介观尺度,基于稠密颗粒离散相模型创建粉体与磨球的仿真模型,选取不同的相对速度法向与切向分量的比值进行仿真,确定粉体的应力能量分布及其粉体数量。在进行介观尺度的仿真之前,需要确定流体中粉体的分布面积。
微观尺度,基于ANSYS的显式动力学建立微观仿真模型,模拟磨球碰撞过程中粉体的应变和能量变化。生成应变和能量变化曲线,与介观仿真得到的粉体应力能量进行比较,得到球磨中粉体破碎前其塑性变形的形变过程以及在该状态下的粉体数量。
1.3 网格无关性验证从理论上来说,随着网格尺寸的不断减小,网格数会随之不断地增加,因为网格数而造成的结果的不同会不断减小直到某一值时则会消失。为了降低网格数对仿真结果的影响,基于5种不同网格数量方案下进行网格无关性验证,以磨球的法向相对速度以及碰撞次数为依据进行对比,对比结果如表 2所示。
| 表 2 网格无关性验证 Table 2 Mesh independence verification |
由表 2可知,方案D、E、F的法向相对速度与碰撞次数差异最小,为了减少计算成本,提高计算效率,最后选择方案E,网格数量为133 988。
1.4 宏观仿真球磨罐体容积为100 mL,工作容积为30 mL,为模拟自由液面条件需保留部分气体,上方多余的气体对仿真结果影响可以忽略不计,因此通过观察1 ∶1模型中液面以及颗粒所处的最高位置进行适当简化,去除多余气体部分体积。模型如图 1所示。

|
图 1 行星球磨机模型 Fig.1 Planetary ball mill model |
本研究在EDEM中使用的接触模型为Hertz-Mindlin(No slip)接触模型,该模型针对颗粒之间的接触力能够准确且有效地进行计算。CFD-DEM耦合界面采用吴亮[16]开发的DEM-VOF模型界面,即含自由液面的气体、液体、固体三相流耦合,并通过颗粒沉降实验验证了DEM-VOF模型能够正确计算并耦合颗粒-流体相互作用力。VOF模型是用于追踪流体与流体之间的相界面的数值模型,DEM模型是颗粒与颗粒之间相互作用的接触模型。此外,该界面采用Reynolds湍流模型来模拟湍流流动,并且为了描述流体和颗粒之间的相间体积置换,开发了一种新的虚拟双网格空隙率模型。
VOF-DEM能够计算流体自由表面和粒子运动。在该模型中,曳力以及一些其他力,如压力梯度力、雷诺应力、升力等都已添加。
1.5 介观仿真介观仿真通过建立碰撞时磨球、粉体和流体之间的相互作用来计算粉体的应力概率。因为粉体的密度比无水乙醇大,而且它在无水乙醇中具有悬浮性,这会使Al粉在无水乙醇中的分布情况是处于非均匀状态的[17],因此在建立介观模型之前,需要确定粉体的分布区域。由于粉体和球磨机之间存在较大的尺寸差异,因此使用稠密颗粒离散相模型来模拟粉体的运动。在确定粉体分布区域之后,计算相邻粉体的质量中心之间的距离,用于后续建立粉体应力概率分析模型。
建立粉体应力概率分析模型,同样采用稠密颗粒离散相模型。设置磨球沿固定方向运动,在磨球运动的区域生成颗粒即粉体。采用动网格来完成磨球的运动,能够精确地将磨球运动时其附近流场发生的变化和Al粉受到的影响反映出来。在磨球碰撞的路径及其周围区域生成粉体,确保粉体分布区域能够覆盖流场运动变化区域,然后通过编译profile文件对磨球运动进行描述。在仿真结束后,对撞击区域内受撞击的粉体数量进行统计,最后计算每个粉体上的应力能量分布。
1.6 微观仿真常用粘结颗粒模型描述颗粒塑性变形,但需要创建大量颗粒以减少误差。大量的颗粒不可避免地增加了计算成本。因此,这种描述材料塑性变形过程的方法是不合适的。在本研究中使用有限元方法对粉体的塑性变形过程进行仿真。虽然有限元仿真可以准确地描述材料塑性变形中的能量变化,但它不能准确地解释材料断裂或断裂时的能量变化,所以仿真部分只用于讨论粉体的塑性变形过程。
在微观仿真中,ANSYS的显式动力学方法将用于建立粉体的塑性变形模型。建立5 μm的粉体模型,为了减少仿真计算成本,在粉体的两端建立固定运动速度且运动方向相对的几何体代替磨球运动,然后对粉体进行压缩。几何体与粉体的接触表面为平面,其中几何体的材料为氧化锆。采用Johnson-Cook材料模型,其能使粉体在高应变和高应变率下的形变得到有效的描述。
2 仿真结果与讨论 2.1 磨球碰撞的相对速度分布在宏观仿真中,磨球碰撞时的相对速度的动能近似于应力能量,碰撞能量表示应力能量的上限。此外,粉体的应力概率直接受磨球相对速度的法向和切向分量分布的影响。因此,分析磨球碰撞过程中法向相对速度(vn)和切向相对速度(vt)的分布是必要的。
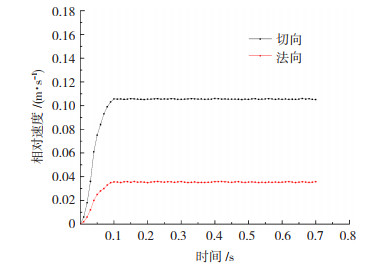
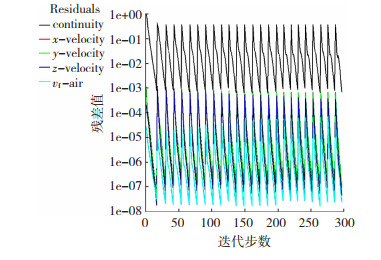
图 2为磨球法向相对速度与切向相对速度随时间变化的曲线图,图 3为仿真过程中各变量的残差值以及各变量的残差标准。由图 2可知,磨球的相对速度在0~0.1 s内迅速提高,然后趋于稳定。磨球运动规律的稳定性是判断球磨是否达到稳定的重要标准。由图 3可知,在仿真的过程中,每迭代一定时间步长,各变量残差值均下降至10-3,达到残差标准,表明仿真结果非常稳定。综上所述可知,该仿真结果是收敛的。
|
图 2 相对速度变化曲线 Fig.2 Relative velocity variation curve |
|
图 3 各变量残差值 Fig.3 Residual values of each variable |
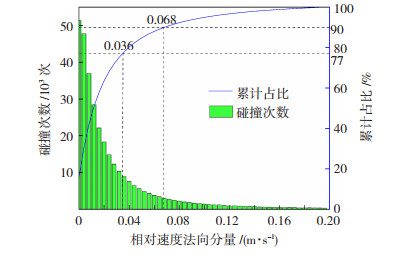
由于磨球在短时间内的碰撞次数多,无法分析每次碰撞时的相对速度。因此,将相对速度的法向分量和切向分量的总体分布的区间划分为一个区域,并计算区间内的碰撞次数。在仿真处于稳定状态后,选取0.50~0.52 s内的数据进行分析。图 4为磨球碰撞的相对速度法向分量的分布情况。横坐标为磨球法向相对速度,左纵坐标为磨球每个时间段的碰撞次数,右纵坐标为磨球每个时间段的碰撞次数对于总的碰撞次数的占比情况。可以看到,碰撞次数整体的分布情况呈幂律分布,磨球的碰撞较多发生在法向相对速度低的区域,磨球的碰撞次数随着法向相对速度的逐渐增大而开始快速降低。其中,法向相对速度的平均值为0.036 m/s,77%的碰撞低于该平均值,只有10%的碰撞频率大于0.068 m/s。
|
图 4 球法向相对速度分布情况 Fig.4 Distribution of normal relative velocity of grinding ball |
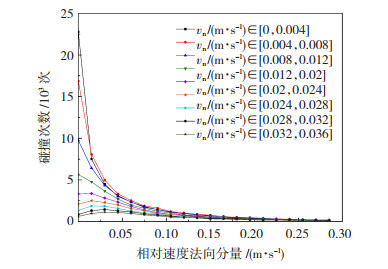
将低于0.036 m/s的法向相对速度分为9个区间,对每个区间所对应的切向相对速度频率分布进行分析,以研究法向相对速度和切向相对速度之间的关系,如图 5所示,随着法向相对速度的增大,切向相对速度的分布情况变得更加平稳。由上述结论可知,切向相对速度的分布情况会受到法向相对速度的影响。
|
图 5 磨球切向相对速度分布情况 Fig.5 Distribution of tangential relative velocity of grinding ball |
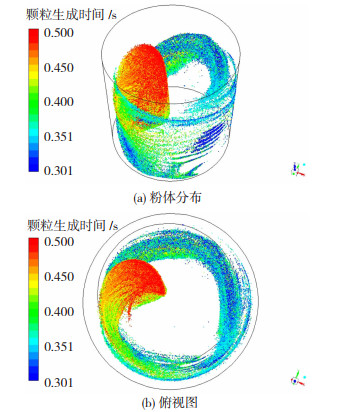
图 6给出了仿真处于稳定状态时球磨罐内粉体的分布区域。由于粉体的密度比无水乙醇大,并且粉体受到离心力的作用,使粉体的运动分布主要靠近于罐壁区域。计算粉体运动分布与磨球运动重合区域的流体体积为1.41×10-5 m3。实验中加入粉体数量约为1.22×1011。基于上述参数,计算出粉体质心之间的距离为4.9×10-3 mm。
|
图 6 粉体运动分布规律 Fig.6 Distribution law of powder movement: (a)powder distribution; (b)vertical view |
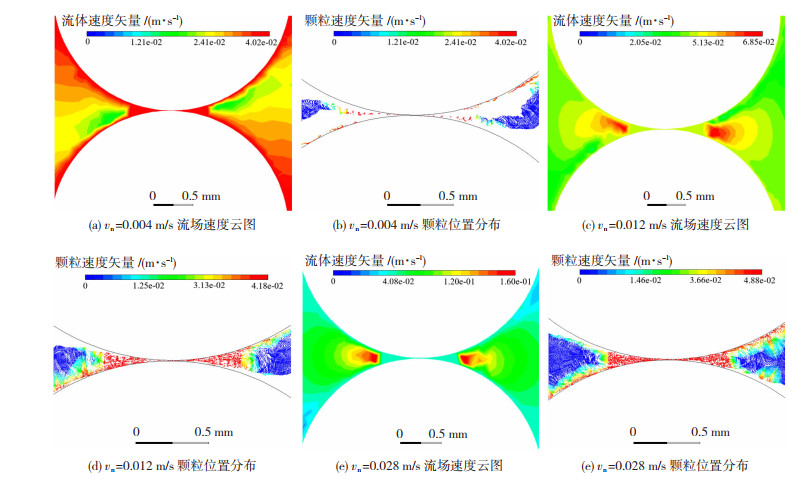
对磨球的法向相对速度分别选取0.004、0.008、0.012、0.016、0.020、0.024、0.028 m/s,切向相对速度选取0.02、0.04、0.08 m/s,合计21种组合进行仿真。图 7所示为当切向相对速度为0.04 m/s,法向相对速度为0.004、0.012、0.028 m/s时,其碰撞区域的流场速度云图和受应力作用的粉体分布情况。对比流场速度云图可知,法向相对速度越大,对流场速度的影响更加显著,从而,当相对速度切向分量保持不变时,相对速度法向分量越高,受应力作用的粉体数量越多。
|
图 7 法向相对速度为变量时流场速度云图与粉体分布 Fig.7 Velocity nephogram of flow field and powder distribution when normal relative velocity is a variable: (a), (b) flow field velocity cloud map and particle position distribution at vn=0.004 m/s; (c), (d) flow field velocity cloud map and particle position distribution at vn=0.012 m/s; (e), (f) flow field velocity cloud map and particle position distribution at vn=0.028 m/s |
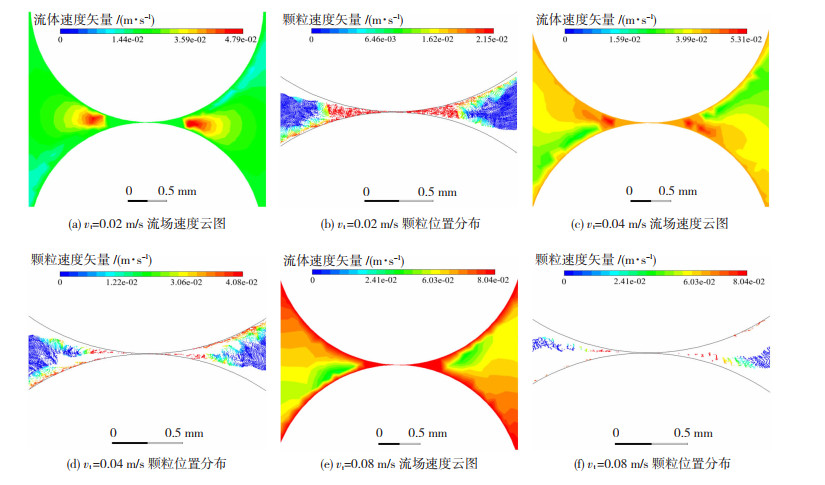
图 8所示为当法向相对速度为0.008 m/s,切向相对速度分别为0.02、0.04、0.08 m/s时,其碰撞区域的流场速度云图和受应力作用的粉体分布情况。当切向相对速度与法向相对速度之比变大时,流场速度云图发生显著的变化,相应受应力作用的粉体数量随之减小。结果表明,当法向相对速度保持恒定时,随着切向相对速度的变大,使磨球发生碰撞时,其碰撞点的附近的流场速度也随之变大,从而使受应力作用的粉体数量降低。由图 7(a)与图 8(e)可知,二图的切向相对速度与法向相对速度之比皆为10,流场速度云图相同,且对应的受应力作用的粉体数量相同,因此受应力作用的粉体的数量与切向和法向相对速度之比有一定关系。
|
图 8 切向相对速度为变量时流场速度云图与粉体分布 Fig.8 Velocity nephogram of flow field and powder distribution when tangential relative velocity is a variable: (a), (b) flow field velocity cloud map and particle position distribution at vt=0.02 m/s; (c), (d) flow field velocity cloud map and particle position distribution at vt=0.04 m/s; (e), (f) flow field velocity cloud map andparticle position distribution at vt =0.08 m/s |
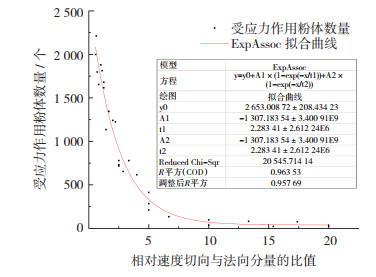
基于21种不同相对速度切向与法向分量比值组合的仿真结果进行分析,其中对于切向与法向比数值跨度较大的区间进行补充仿真,以确定受应力作用的粉体数量与法向和切向相对速度之比的关系。图 9所示为不同法向与切向相对速度之比和对应的受应力作用的粉体数量所生成的拟合曲线。该拟合曲线的R2为0.963 53,其值近似于1,说明拟合曲线具有良好且稳定的预测性。该拟合曲线可用于预测粉体在不同相对速度下的应力概率,然后计算每个粉体上的应力能量分布。
|
图 9 ExpAssoc拟合曲线 Fig.9 ExpAssoc fitting curve |
作为一种塑性材料,即使碰撞中的应力能量很小,粉体也会变形。因此,每次碰撞都是有效的碰撞。当碰撞中的粒子数量太少时,碰撞能量转化为粉体变形的应力能量的效率下降。当相对速度切向分量与法向分量之比大于10时,冲击粉体的数量预计低于60,应力能量转化效率降低。由于在这种情况下受影响的粉体数量很少,因此该部分粉体的变形暂时未放在研究中。应力能量基于EDEM仿真中磨球碰撞时的相对速度的动能
来近似。每次碰撞的应力能可由下式计算
| $ S E=\frac{1}{2} m\left(v_{\mathrm{n}}^2+v_{\mathrm{t}}^2\right) $ | (1) |
式中:SE为应力能;vn为相对速度法向分量;vt为相对速度切向分量。
| $ n=2.617 \times 10^{10}\left(\frac{v_{\mathrm{t}}}{v_{\mathrm{n}}}+12.205\right)^{-6.409} $ | (2) |
式中:n为受撞击粉体数量。
| $ S E_{\text {Pow }}=S E / n $ | (3) |
式中:SEPow为粉体应力能量。
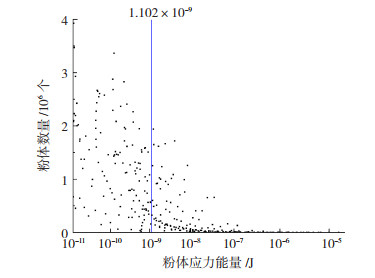
图 10显示了粉体应力能量的频率分布。粉体应力能量的主要分布区间为3.57×10-10~1.39×10-7 J。
|
图 10 粉体应力能量分布 Fig.10 Stress energy distribution of powder |
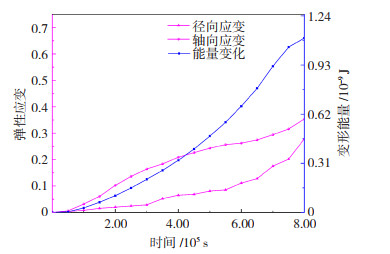
在微观仿真中,几何体的固定运动速度设置为0.025 m/s,两个运动方向相反。粉体的塑性变形阶段的仿真时间为0~8×10-5 s。图 11所示为粉体能量变化、轴向应变和径向应变。由于几何体施加了固定的速度限制,轴向应变呈上升趋势变化。通过将粉体的应力能量分布与塑性变形能量变化进行比较,可以观察到撞击后粉体的形态分布。塑性变形阶段的最高能量变化为1.102×10-9 J。结合图 10可得,粉体应力能量1.102×10-9 J以下数量占比为48.75%。该部分粉体的塑性变形规律可以得到表征,超过1.102× 10-9 J的粉体将不同程度地断裂或破碎。
|
图 11 粉体塑性变形应变和能量变化曲线 Fig.11 Plastic deformation strain and energy change curve of powder |
基于QM-3SP04行星式球磨机进行了Al /PTFE复合材料的球磨实验,实验参数如表 3所示。
| 表 3 Al/PTFE球磨实验参数 Table 3 Ball milling experimental parameters of Al/PTFE |
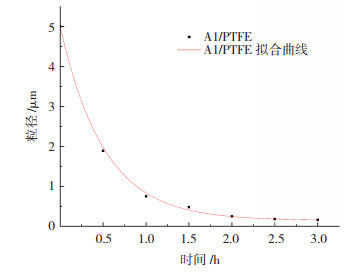
在不同的时间段,将粉碎后的粉体取出来,测定其平均粉体的大小,并观测粉体的形态变化,根据其粒径的变化生成拟合曲线,其判定系数R2为0.99 946,数值接近于1,具有较强的可预测性,拟合曲线如图 12所示。
|
图 12 粒径变化 Fig.12 Change of grain size |
随着研磨时间的延长,Al/PTFE复合材料的粒度逐渐变小并达到其最小尺寸。对各时间点的平均粉体直径进行拟合,它的变化趋势是指数型的,其表达式[18]为
| $d_{\mathrm{p}}(t)=a+b e^{c t} $ | (4) |
式中:t为球磨时间;dp为平均粉体直径;a为平均粉体的最小直径;b为平均粉体球磨前的直径减去平均粉体的最小直径;c为材料破碎速率指数。
在球磨实验过程中,将两次不同时间的物料取出进行测量,则得到平均粉体最小直径和所选两个时间点对应的平均粉体直径,从而取得a、b、c的值。对于相同的粉体,若其球磨冲击载荷条件不发生改变,则c为定值,所以当研磨不同直径的粉体时,只要得到平均粉体直径的最小值,则可以获得在研磨的任何时间点停止时的平均粉体直径。
这些结果对实际的工程有重要的指导意义,在实际的工程中,通常要经过多次的实验才能得到目标粉体的直径,并确定其球磨时长,而当目标粉体直径发生改变后,需要重复以往的多次实验再次获得对应的球磨时长。而基于上述的结论,通过单次的研磨,能够确定将粉体直径研磨到任何粒度所需要的时间,从而可有效的避免由于所需的粉体直径发生改变而进行的多次实验,使粉体的研磨得到科学指导,避免了由于不合理的球磨实验所带来的人力、财力、物力以及时间的浪费。
4 结论本研究的主要目的是采用多尺度仿真与球磨实验结合,以了解行星球磨中微米级铝粉破碎前的塑性变形以及破碎后粒径变化的过程。
1) 宏观仿真建立球磨罐、磨球和流体的模型,对磨球发生碰撞过程中的法向相对速度和切向相对速度进行统计分析,发现不同相对速度的法向分量与切向分量的分布呈幂律分布。当相对速度法向分量上升时,相应的切向分量呈现总体上升趋势。
2) 介观仿真建立粉体与磨球的2D模型,结合磨球的切向与法向相对速度的比值,得到粉体应力能量分布及其粉体数量;微观仿真获得粉体塑性变形的应变和能量变化曲线。结果表明,受应力作用的粉体数量随磨球碰撞相对速度的切向分量和法向分量之比的增大而减小;对比粉体塑性变形的应变和能量变化曲线与粉体应力能量分布,可以得到粉体发生塑性变形的形变过程以及在该状态下的粉体数量,且塑性变形阶段的最高能量为1.102×10-9 J,粉体应力能量在1.102×10-9 J以下数量占比为48.75%。
3) 根据粉体破碎后粒径的变化生成拟合曲线,其判定系数R2为0.999 46,数值接近于1,具有较强且稳定的可预测性,结合仿真得到的破碎前粉体的塑性变形的变化过程,可以实现对球磨任意时间后的颗粒粒径的预测,使粉体的研磨得到科学指导,避免了由于不合理的球磨实验所带来的人力、财力、物力以及时间的浪费。
| [1] |
WANG Haifu, GENG Baoqun, GUO Huanguo, et al. The effect of sintering and cooling process on geometry distortion and mechanical properties transition of PTFE/Al reactive materials[J]. Defence Technology, 2020, 16(3): 720-730. DOI:10.1016/j.dt.2019.10.006 |
| [2] |
XIAO Jianguang, NIE Zhengyuan, WANG Zhao, et al. Energy Release behavior of Al/PTFE reactive materials powder in a closed chamber[J]. Journal of Applied Physics, 2020, 127(16): 165106. DOI:10.1063/5.0004191 |
| [3] |
WANG Jun, JIANG Xiaojun, ZHANG Long, et al. Design and fabrication of energetic superlattice like PTFE/Al with superior performance and application in functional micro-initiator[J]. NanoEnergy, 2015, 12: 597-605. DOI:10.1016/j.nanoen.2014.12.016 |
| [4] |
NIE Hongqi, CHAN H Y, PISHARATH S, et al. Combustion characteristic and aging behavior of bimetal thermite powders[J]. Defence Technology, 2021, 17(3): 755-762. DOI:10.1016/j.dt.2020.05.009 |
| [5] |
HUANG Chuan, JIAN Guoqiang, DELISIO J B, et al. Electrospray deposition of energetic polymer nanocom posites with high mass particle loadings: A prelude to 3D printing of rocket motors[J]. Advanced Engineering Materials, 2015, 17(1): 95-101. DOI:10.1002/adem.201400151 |
| [6] |
NICOLLET A, LAHINER G, BELISARIO A, et al. Investigation of Al/CuO multilayered thermite ignition[J]. Journal of Applied Physics, 2017, 121(3): 034503. DOI:10.1063/1.4974288 |
| [7] |
敖文, 刘佩进, 吕翔, 等. 固体推进剂燃烧过程铝团聚研究进展[J]. 宇航学报, 2016, 37(4): 371-380. AO Wen, LIU Peijin, LV Xiang, et al. Review of aluminum agglomeration during the combustion of solid propellants[J]. Journal of Astronautics, 2016, 37(4): 371-380. DOI:10.3873/j.issn.1000-1328.2016.04.001 |
| [8] |
SIPPEL T R, SON S F, GROVEN L J. Aluminum agglomeration reduction in a composite propellant using tailored Al/PTFE particles[J]. Combustion & Flame, 2014, 161(1): 311-321. DOI:10.1016/j.combustflame.2013.08.009 |
| [9] |
ZYRYANOV V. Processing of oxide ceramic powders for nanomaterials using high-energy planetary mills[J]. Interceram, 2003, 52(1): 22-27. DOI:10.1016/S0079-6425(03)00034-3 |
| [10] |
裴英杰, 肖庆飞, 石贵明, 等. 离散元法在球磨机仿真中的研究进展及应用[J]. 黄金, 2022, 43(1): 69-77. PEI Yingjie, XIAO Qingfei, SHI Guiming, et al. Research progress and application of discrete element modeling in ball mill simulation[J]. Gold, 2022, 43(1): 69-77. DOI:10.11792/hj20220112 |
| [11] |
JIANG S Q, YE Y X, TAN Y Q, et al. Discrete element simulation of particle motion in ball mills based on similarity[J]. Powder Technology, 2018, 335: 91-102. DOI:10.1016/j.powtec.2018.05.012 |
| [12] |
BEINERT S, FRAGNIERE G, SCHILDE C, et al. Multiscale simulation of fine grinding and dispersing processes: Stressing probability, stressing energy and resultant breakage rate[J]. Advanced Powder Technology, 2018, 29(3): 573-583. DOI:10.1016/j.apt.2017.11.034 |
| [13] |
BEINERT S, KWADE A, SCHILDE C. Strategies for multi-scale simulation of fine grinding and dispersing processes: Drag coefficient and fracture of fractal aggregates[J]. Advanced Powder Technology, 2018, 29(3): 707-718. DOI:10.1016/j.apt.2017.12.012 |
| [14] |
陶俊, 王晓峰, 韩仲熙, 等. 铝粉/聚四氟乙烯机械活化含能材料的制备及其微观性能研究[J]. 材料导报, 2018, 32(6): 894-898. TAO Jun, WANG Xiaofeng, HAN Zhongxi, et al. Preparation and microstructure of aluminum powder/polytetrafluoroethylene mechanical activated energetic composites[J]. Material Introduction, 2018, 32(6): 894-898. DOI:10.11896/j.issn.1005-023X.2018.06.008 |
| [15] |
CHANG Q, DI S B, XU J, et al. Direct numerical simulation of turbulent liquid-solid flow in a small-scale stirred tank[J]. Chemical Engineering Journal, 2021, 420: 127-562. DOI:10.1016/j.cej.2020.127562 |
| [16] |
吴亮. 含固体颗粒的两相流界面变化的数值研究——DEM-VOF方法的实现[D]. 天津: 天津大学, 2018. WU Liang. Development of a DEM-VOF model for the turbulent free-surface flows with particle[D]. Tianjin: Tianjin University, 2018. DOI: 10.7666/d.D01679324 |
| [17] |
SUN Z N, ZHU J. A four-quadrant flow regime map for two-phase liquid-solids and gas-solids fluidization systems[J]. Powder Technology, 2021, 394: 424-438. DOI:10.1016/j.powtec.2021.08.050 |
| [18] |
李旭, 刘彦, 安丰江, 等. 行星式球磨颗粒流场分布与形貌变化规律[J]. 兵工学报, 2022, 43(4): 876-891. LI Xu, LIU Yan, AN Fengjiang, et al. Flow field distribution and morphology variation of particles in planetary ball milling[J]. Acta Armamentarii, 2022, 43(4): 876-891. DOI:10.12382/bgxb.2021.0252 |
 2024, Vol. 32
2024, Vol. 32


