| Author Name | Affiliation | | Yadan Wang | Department of Mathematics, Xidian University, Xi’an 710126, China | | Hongwei Liu | Department of Mathematics, Xidian University, Xi’an 710126, China
School of Mathematics and Computer Science, Hezhou University, Hezhou 542899, Guangxi, China |
|
| Abstract: |
| This paper proposes a new full Nesterov-Todd (NT) step infeasible interior-point algorithm for semidefinite programming. Our algorithm uses a specific kernel function, which is adopted by Liu and Sun, to deduce the feasibility step. By using the step, it is remarkable that in each iteration of the algorithm it needs only one full-NT step, and can obtain an iterate approximate to the central path. Moreover, it is proved that the iterative bound corresponds with the known optimal one for semidefinite optimization problems. |
| Key words: semidefinite programming infeasible interior-point methods full Nesterov-Todd steps kernel functions polynomial complexity |
| DOI:10.11916/j.issn.1005-9113.17078 |
| Clc Number:O221.2 |
| Document Code::A |
| Fund: |
|
| Descriptions in Chinese: |
| 半定规划基于特殊核函数的全牛顿步不可行内点算法 王亚丹1,刘红卫1,刘泽显1,2 (1. 西安电子科技大学 数学与统计学院,西安 710126; 2. 贺州学院 数学与计算机学院,广西 贺州 542899) 创新点说明:本文利用特殊的核函数改进算法的可行步,构造了相应的不可行内点算法,使得算法在每次迭代过程中只需一次全牛顿步,就能够得到接近中心路径的新的迭代点。 研究目的: 通过使用核函数改进可行步,提出一种新的全牛顿步不可行内点算法。 研究方法: 定量分析法;对比分析法; 数学实验法。 研究结果、结论: 1)通过使用特殊的核函数改进可行步,得到了一种新的半定规划不可行内点算法; 2)算法在每次迭代过程中仅使用一次可行步,就能够得到半定规划问题的近似最优解; 3)对算法进行复杂性分析,得到算法的迭代复杂度为 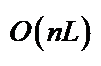 ,其中 ,其中 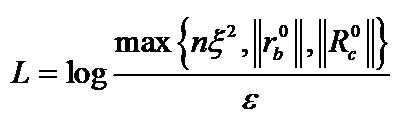 ,结果表明:算法的迭代复杂度与目前半定规划最好的迭代复杂度一致。 ,结果表明:算法的迭代复杂度与目前半定规划最好的迭代复杂度一致。 关键词:半定规划,不可行内点算法,全牛顿步,核函数,多项式复杂度 |




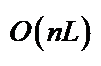 ,其中
,其中 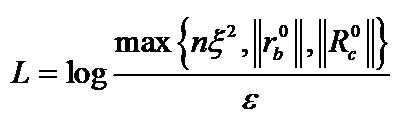 ,结果表明:算法的迭代复杂度与目前半定规划最好的迭代复杂度一致。
,结果表明:算法的迭代复杂度与目前半定规划最好的迭代复杂度一致。