摘要
为满足型钢混凝土(steel reinforced concrete,SRC)结构地震损失评估及抗震韧性评价的需求,建立 SRC 柱构件的地震易损性函数十分关键。本文首先基于文献调研,结合 JGJ 138—2016《组合结构设计规范》,从国内外文献中筛选了 227 榀拟静力循环加载的 SRC 柱,建立标准化的 SRC 柱试验数据库。其次,考虑失效模式的差异性,将构件分为延性 SRC 柱和偏脆性 SRC 柱,并给出了不同类别的构件损伤等级划分标准及对应的修复方法。然后,以位移角为工程需求参数,分别提取了各构件对应不同损伤等级的位移角限值,采用 FEMA P-58 方法,建立了不同类别的 SRC 柱在各损伤等级下的易损性函数。最后, 给出了与 GB/ T 38591—2020《建筑抗震韧性评价标准》相容的易损性函数参数表,并分析了抗震等级和轴压比对 SRC 柱易损性函数参数及易损性曲线的影响。最终,通过分析一幢型钢混凝土框架结构办公楼的抗震韧性,说明了所提出的易损性函数在抗震韧性评价中的作用。
Abstract
To meet the needs of earthquake losses and structural seismic resilience evaluation, it is key to establish the seismic fragility functions. A database containing 227 SRC columns under repeated cyclic loads is established based on the existed experiments in this study. All the SRC columns satisfy the requirements of the Chinese ‘code for design of composite structures’(JGJ 138—2016). Considering the difference in failure model, the components are divided into ductile SRC columns and brittle SRC columns. The damage state classification criteria and corresponding repair methods for different groups are given. Then, the drift is taken as the engineering demand parameter (EDP), the drift limits of each column corresponding to different damage states are extracted based on the hysteresis information. After that, the fragility functions of SRC columns under different groups and damage states are developed using FEMA P-58 method. Finally, the table of fragility function parameters that compatible with the ‘standard for seismic resilience assessment of buildings’ (GB / T 38591—2020) is given. The effects of seismic grade and axial load ratio on the fragility function parameters and fragility curve of SRC columns are compared. The role of the proposed fragility function in seismic resilience evaluation is demonstrated, by analyzing the seismic resilience of an SRC frame structure office building.
近年来的震害调查结果表明,基于中国规范设计的建筑物具有较高的抗倒塌安全储备,在地震中鲜有倒塌,但仍有重度破坏风险,破坏严重者整体结构需拆除重建[1]。上述问题造成了极高的经济损失,严重影响社会的可持续发展。因此,针对建筑结构的抗震性能评价不仅需关注其安全性,亦需关注其抗震韧性。
中国于 2020 年颁布的 GB / T38591—2020 《建筑抗震韧性评价标准》 [2] 给出了针对既有建筑的抗震韧性评价流程。其中,构件易损性函数描述了构件在地震中处于不同损伤状态的可能性,是计算结构震后直接经济损失和间接经济损失的重要依据。此前,国内外关于易损性函数研究已取得一些相关研究成果。如 FEMA P-58 项目研究期间,Brown 等[3]结合 106 榀钢筋混凝土( reinforced concrete,RC)构件建立了满足不同抗震构造措施的 RC 框架柱易损性函数; Goksu [4] 采用 33 榀 RC 框架及框架柱的试验数据建立了再生混凝土柱构件的易损性函数,并与普通混凝土柱试件进行了对比,表明在高损伤状态下再生混凝土柱的损伤超越概率高于普通柱; Cardone [5]基于 18 榀 RC 柱构件的拟静力试验数据,建立了满足 20 世纪 70 年代前非抗震构造 RC 柱构件的易损性函数; Yurdakul 等[6] 构建了 FRP 加固的钢筋混凝土梁柱节点的易损性函数。国内,《建筑抗震韧性评价标准》 [2]给出压弯破坏的 RC 柱对应各极限状态的位移角取值及对数标准差; 谢贤鑫等[7]建立了不同类型砌体填充墙对应于不同损伤状态的易损性曲线,分析了砌体填充墙的破坏特征和变形能力; 纪晓东等[8] 分别采用位移角和连梁转角为指标参量,建立了 RC 剪力墙和连梁的易损性曲线; 代旷宇等[9-11]建立了满足中国现有规范的未锈蚀及锈蚀的 RC 框架柱构件易损性函数,结果表明高锈蚀损伤会造成试件位移能力的明显下降,并会降低易损性曲线的不确定性。值得说明的是,虽然上述研究给出了各类 RC 柱构件的易损性函数,但既有的 RC 柱构件的易损性函数并不适用于建筑结构中的 SRC 柱,这限制了《建筑抗震韧性评价标准》 [2] 在实际工程中的应用。此外,由于 SRC 柱承载能力高及抗震性能良好,其被广泛用于高烈度区,故建立 SRC 柱易损性函数十分必要。
鉴于此,本文主要研究 SRC 柱的易损性函数。首先建立了含有 227 榀 SRC 柱的拟静力试验数据库。其次,以位移角为工程需求参数,提取了不同损伤等级下 SRC 柱位移角限值。基于 FEMA P-58 方法建立了 SRC 柱的易损性函数,并完成了拟合优度检验。然后,讨论了抗震等级及轴压比对 SRC 柱易损性曲线的影响。最后,结合一个型钢混凝土组合框架的分析案例,阐述了 SRC 柱的易损性函数在型钢混凝土组合结构抗震韧性分析中的作用。
1 SRC 柱试验数据库的建立
目前,国内外在往复荷载作用下 SRC 结构抗震性能方面已积累了大量的试验资料[1,12-36],这为建立 SRC 柱的易损性函数提供了数据基础。为满足中国 SRC 结构抗震韧性评价的实际需要,参考《组合结构设计规范》 [37],考虑构件的含钢率 ρss、纵筋配筋率 ρl、体积配箍率 ρsv、设计轴压比 nd、翼缘宽厚比 bf / t f、腹板宽厚比 hw / tw及箍筋间距 s 等构造要求对 SRC 柱进行筛选。规范中对各参数的构造要求及参数计算公式见表1。
表1SRC 柱筛选准则
Tab.1 The criteria of selecting the SRC columns

注:Ass、Ac、Ag、Al、Acor 分别为型钢截面面积、混凝土截面面积、柱截面面积、纵筋截面面积、核心区混凝土面积; f ck、f ysk为混凝土轴心抗压强度标准值、型钢屈服强度标准值; γm、γs 为混凝土和型钢的分项系数,参照GB 50010—2010 《 混凝土结构设计规范》,分别取值为 1.4、1.1; Nd = γG × NGk + γQ × NQk,γG为永久荷载的分项系数,γQ为可变荷载的分项系数,参照 GB 50009—2012《建筑结构荷载规范》,分别取值1.2、1.4; NGk、NQk分别为永久荷载和可变荷载; bf、t f、hw、tw 分别为型钢翼缘宽度和厚度、腹板高度和厚度。
根据表1最终筛选出满足规范要求的 SRC 柱试件 227 榀,其设计轴压比 nd、剪跨比 λs(柱有效高度 L 与横截面高度 h 之比)等设计参数的分布情况见图1。值得说明的是,根据数据库中试件加载时的边界条件,其可分为悬臂式和建研式加载,试验加载装置及构件受力简图见图2。其中悬臂式加载由竖向布置的千斤顶与滚轴与试件连接,用于施加恒定的轴向力,水平布置一只制动器与试件铰接,用于施加水平力(图2(a)); 建研式加载装置主要由L 形大梁、平行四连杆和水平制动器等组成(图2( b))。平行四联杆使 L 形大梁在竖向和水平方向自由移动,但不发生转动,从而使柱顶为嵌固端。另外,为统一对比,需对数据进行归一化处理。本文将所有构件的数据转换为假定试件为悬臂柱加载时的力-转角数据。

图1各设计参数分布直方图
Fig.1The distribution of the design parameters of the SRC columns

图2试验加载装置及受力分析模型
Fig.2Test setup and force analysis model
2 SRC 柱损伤等级划分及数据提取
2.1 SRC 柱损伤等级划分及修复方法
由于试件来自不同文献,其在截面尺寸、失效模式等方面有所不同,为考虑这些差异性,更加精确的构建 SRC 柱的易损性函数,需对构件加以区分。 Yao 等[38]的研究表明,剪跨比 λs和弯剪比 m(柱抗弯承载力 Mu与抗剪承载力 Vu之比)是影响构件失效的关键因素,故根据 λs和 m 将 SRC 柱分为延性柱和偏脆性柱。延性柱极限承载力由抗弯承载力 Mu控制,此类试件一般发生弯曲破坏,其破坏特征见图3(a)。偏脆性柱极限承载力由抗剪承载力 Vu 控制,此类试件一般发生剪切破坏,其破坏特征见图3(b)。对于 SRC 柱,Mu 及 Vu 可根据《组合结构设计规范》 [37] 中提供的公式计算。具体划分准则为:若文献中明确给出试件的破坏模式且为弯曲破坏时,则将其归类为延性柱,否则为偏脆性柱; 若文献中没有给出破坏模式,则通过 λs 和 m 划分,当 λs≤2时,为偏脆性柱; 当 λs≥3 时,为延性柱; 当2 <λs <3 时,若 m <1,则为延性柱,否则为偏脆性柱。在所筛选的 227 榀构件中,延性 SRC 柱和偏脆性 SRC 柱的数量分别为 96 榀和 131 榀。
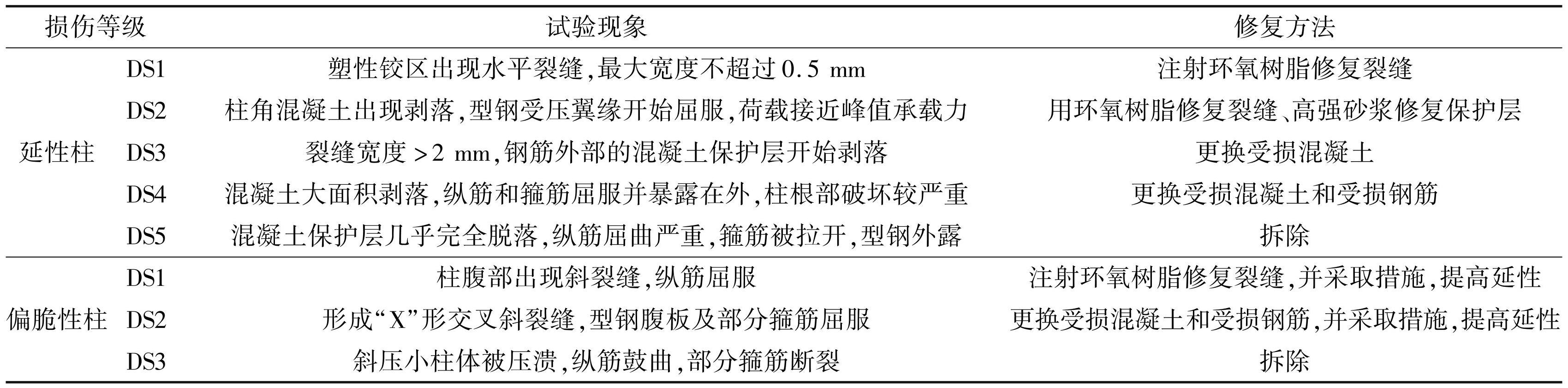
一般而言,延性 SRC 柱变形能力相对较好,不同损伤等级之间破坏特征的差别较为显著,因此本文参考季静等[39-41]的研究将延性 SRC 柱的损伤状态分为 5 个等级(DS1~DS5),分别对应基本完好、轻微、中度、比较严重、严重。偏脆性 SRC 柱变形能力较差,屈服点的位移角与峰值点的位移角相距较近,承载力超过峰值点后迅速下降。因此本文将其损伤状态分为 3 个等级(DS1~DS3),分别对应基本完好、中度、严重。不同类别 SRC 柱各损伤等级对应的典型破坏特征见图3。此外,根据结构韧性评价要求,为确定震后构件的修复费用,需确定构件各损伤等级对应的修复方法。参考 FEMA P-58 [42] 及蒋欢军等[43]的研究,结合文献中各试件试验现象特征,确定不同损伤等级下试件的损伤现象及对应的修复方法,见表2。
图3SRC 柱不同损伤等级对应的破坏特征
Fig.3Failure characteristics of SRC columns with different damage states
表2损伤等级划分及修复方法
Tab.2 Damage classification and corresponding methods of repair for SRC columns
2.2 SRC 柱各损伤等级的数据提取
考虑 SRC 柱损伤等级与位移变形的强相关性,以位移角作为 SRC 柱的工程需求参数,并构建易损性函数。参考季静等[39]的研究,采用图4所示的特征点定义方法确定 SRC 柱在各损伤状态对应的位移角。图4(a)为延性 SRC 柱的试验骨架曲线,其中 A 点为采用 Park 法确定的屈服点,B 点为峰值点,C、D、E 点分别为承载力下降至 90%、80%、70% 峰值荷载时对应的点。 A~E 点对应的 θ1~θ5分别为 DS1~DS5 状态对应的位移角。图4( b)为偏脆性 SRC 柱的试验骨架曲线,采用 θ1 、θ3 、θ5分别作为 DS1~DS3 状态对应的位移角限值,分别对应屈服点、承载力下降至 90% 及 70% 时的点。本文提取了数据库中 SRC 柱在各损伤等级下的位移角数据。

图4SRC 柱损伤等级划分
Fig.4Damage states of SRC columns
3 SRC 柱易损性函数的建立
3.1 易损性函数的定义
构件的易损性函数代表在给定需求参数下,其达到各损伤等级的超越概率,既有研究往往假定构件的易损性函数服从对数正态分布[5]。 SRC 柱第 i 个损伤等级的超越概率 Pi(d)可表达为
(1)
式中:Φ 为标准正态累积分布函数,d 为工程需求参数,为第 i 个损伤等级下 SRC 柱位移角的中位值,βi 为第 i 个损伤等级下的对数标准差。
3.2 易损性函数的参数计算
本文基于对数正态分布计算 SRC 柱各损伤等级的超越概率,参考 FEMA P-58 [42],SRC 柱第 i 个损伤等级对应的位移角限值的中位值 按下式计算:
(2)
式中:θij为第 j 个样本在第 i 个损伤等级对应的位移角限值,Mi为第 i 个损伤等级下剔除离群值后的试验样本数,离群值可采用 Peirce 准则确定[45]。对数标准差 βi 反映了 SRC 数据集中第 i 个损伤等级对应位移角的离散程度。按下式计算:
(3)
式中 βi 源自两部分相互独立的标准偏差,分别是本质不确定性引起对数标准差 βr,i及主观不确定性导致的离散性 βu,i。对于 βu,i可参考 FEMA P-58 建议取值为 0.1。 βr,i可由下式计算:
(4)
此外,在建立易损性函数时,有可能遇到两条曲线交叉的情况,而对于这种情况则需采用式(5)~(6)对中位值和对数标准差进行修正:
(5)
(6)
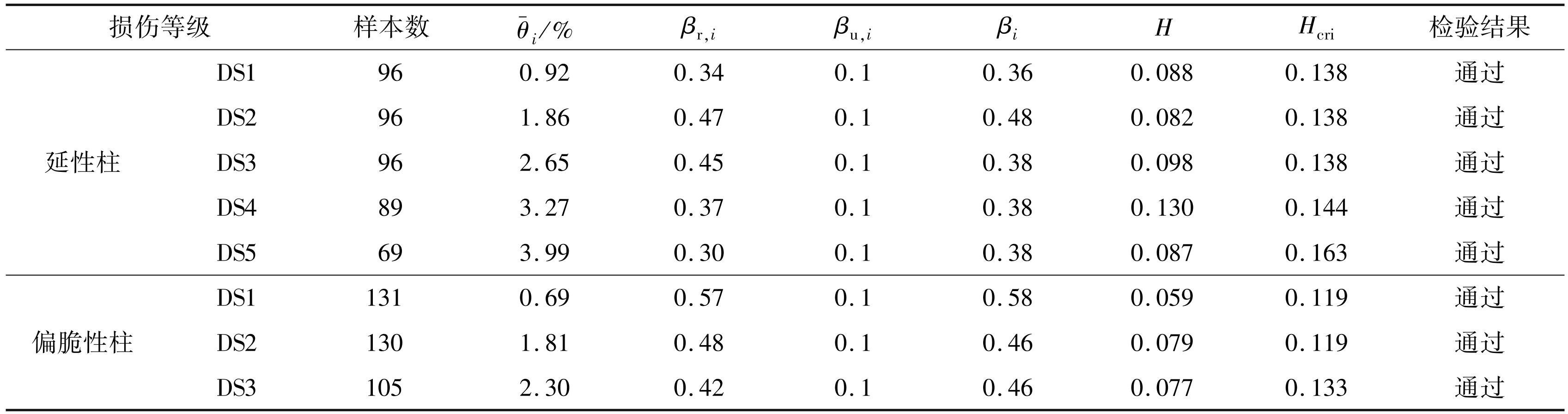
式中:N 为交叉易损性曲线的数量,β′i为修正后对数标准差,为修正后位移角限值的中位值。根据式(2)~(6),可求得 SRC 柱各损伤状态对应的易损性函数参数值,见表3。
表3SRC 柱易损性函数参数及拟合优度检验结果
Tab.3 Fragility function parameters and Kolmogorov-Smirnov test results of SRC columns
3.3 SRC 柱易损性曲线
图5为 SRC 柱各损伤等级下的试验样本点及利用式(1)计算得到的易损性曲线。由图5可知,SRC 柱对应的各损伤等级易损性曲线与试验数据的累积频数分布较为吻合,各损伤等级的试验数据基本符合对数正态分布的假设。由图5(a)可看出延性 SRC 柱在 DS4~DS5 状态之间的差异性相较于其余相邻损伤等级间的差异性较小,这是由于 SRC 试件在 DS4 状态之后处于加载阶段末期,试件承载力处于较快下降阶段,使得 DS4 与 DS5 对应的位移角接近所导致。此外,对比相同损伤等级下延性和偏脆性试件的易损性曲线,可发现在相同的位移角下偏脆性试件的超越概率要远高于延性试件,这是由偏脆性试件的变形能力普遍低于延性试件所导致的。

图5SRC 柱的易损性曲线
Fig.5Fragility curves of SRC columns
3.4 拟合优度检验
为验证易损性函数服从对数正态分布的假设,利用 Kolmogorov-Smirnov(K-S)检验[46],通过计算拟合曲线的累积概率分布和试验样本计算的频数分布二者的最大差值 H 并与显著性水平取 5% 时对应的限值 Hcri比较,结果见表3。由表3可知,在 5% 显著水平下,延性 SRC 柱和偏脆性 SRC 柱各损伤等级均通过检验,表明本文构建的易损性函数均服从对数正态分布。
3.5 与 RC 柱易损性函数的对比
将本文建立的延性 SRC 柱易损性函数与文献[10]中以弯曲破坏为主建立的 RC 柱易损性函数对比,结果见表4。不难发现,除 DS5 外,SRC 柱易损性函数的中位值整体上高于 RC 柱,说明 SRC 柱的变形能力要高于 RC 柱。然而 DS5 状态下 SRC 位移角中值略小于 RC 柱,其原因是本文的试验样本中设计轴压比大于 0.5 的试件约占 60% 左右,而增加轴压比会显著降低构件的极限变形能力。此外,对比二者的对数标准差,发现文献[10] 结果普遍小于本文研究结果,这可能是由其主要设计参数的变异程度比本文小所导致的。
需说明的是,本文的易损性函数是基于 JGJ 138—2016《组合结构设计规范》 [37] 筛选试验数据建立的,满足既有工程中绝大部分 SRC 柱评估需求。然而,当 SRC 柱设计参数超出表1范围时,则不宜未加论证而直接采用。
表4延性 SRC 柱与 RC 柱易损性函数参数对比
Tab.4 Comparison of fragility function parameters between ductile SRC columns and RC columns

4 影响因素分析
参考《建筑抗震韧性评价标准》 [2],以抗震等级及设计轴压比为关键因素,进行易损性分组。依据 《组合结构设计规范》 [37],根据配箍特征值及轴压比限值划分试件抗震等级,分别为一级、二级和三、四级三类。考虑《组合结构设计规范》中规定 SRC 柱的最大设计轴压比为 0.95,本文将 nd≤0.5 的试件定义为低轴压比试件,nd >0.5 的试件定义为高轴压比试件。然后,引入超越概率之差 ΔPf这一概念,以便更加直观地分析不同因素对 SRC 柱地震易损性曲线的影响,其定义为在相同的损伤状态下两条易损性曲线超越概率的差值,计算公式为
(7)
式中 Pf1、Pf2为不同因素下 SRC 柱两条易损性曲线的超越概率。 ΔPf 越大,该因素对构件易损性曲线的影响越显著。
4.1 抗震等级的影响
表5为不同抗震等级 SRC 柱易损性函数参数值和 βi。可以看出,在相同轴压比分组下,抗震等级越高越大。在相同的损伤状态及抗震等级下,低轴压比试件的易损性函数中位值总是高于高轴压比试件。需要指出,抗震等级一级与二级的 SRC 柱各损伤状态对应的易损性函数中位值及对数标准差相差不大。因此,本文重点对比了三、四级和一级 SRC 柱易损性曲线上超越概率的差值 ΔPf,见图6。由图6可看出三、四级框架柱的超越概率高于一级框架柱,说明三、四级框架柱的抗震能力较差。此外,在低轴压比及相同损伤状态下,偏脆性 SRC 柱的 ΔPf,max(27%~40%)要明显高于延性 SRC 柱(18%~25%)。而在高轴压比下,除偏脆性构件的 DS1 状态外,抗震等级对 SRC 柱 ΔPf,max的影响并不显著,其范围为 4%~22%。
表5不同抗震等级下 SRC 柱易损性参数计算结果
Tab.5 The results of fragility parameters of SRC columns under different seismic grades

图6三、四级框架柱和一级框架柱的 ΔPf
Fig.6ΔPf between SRC columns with first and third / fourth
4.2 轴压比的影响
图7为延性及偏脆性一级、二级及三、四级框架柱在高/ 低轴压比工况下各损伤等级超越概率差值 ΔPf的结果。由图7可知,轴压比对延性构件各损伤等级下 ΔPf,max的影响范围为 38%~63%; 对偏脆性构件 ΔPf,max影响范围为 20%~54%。此外,在不同抗震等级下,延性构件各损伤等级对应的 ΔPf,max 大部分情况下高于偏脆性构件,说明轴压比对延性构件各损伤等级下易损性曲线超越概率的影响更显著。此外,随着抗震等级降低,延性 SRC 柱在高/ 低轴压比工况下的 ΔPf,max逐渐降低。对于延性一级框架柱,其在高/ 低轴压比下各损伤等级对应的 ΔPf,max 均在 45% 以上,最大为 63%; 对于三、四级框架,其 ΔPf,max介于 38%~48%。对于偏脆性一级框架柱,其在高/ 低轴压比下各损伤等级的 ΔPf,max 介于 21%~45%; 对于三、四级框架,其 ΔPf,max 介于 20%~23%; 偏脆性二级框架柱 ΔPf,max介于一级和三、四级之间。偏脆性 SRC 柱在高/ 低轴压比工况下的 ΔPf,max总体上亦随抗震等级的降低而减小,但其受轴压比影响不如延性 SRC 柱明显。
图7高/ 低轴压比下 SRC 柱的 ΔPf
Fig.7ΔPf between SRC columns with high and low axial load ratio
5 基于易损性函数的抗震韧性评价
为说明 SRC 柱地震易损性函数在结构抗震韧性评价中的作用。依据 《 建筑抗震韧性评价标准》 [2]提供的抗震韧性评价框架(图8),以一个型钢混凝土框架为例,分析结构韧性。
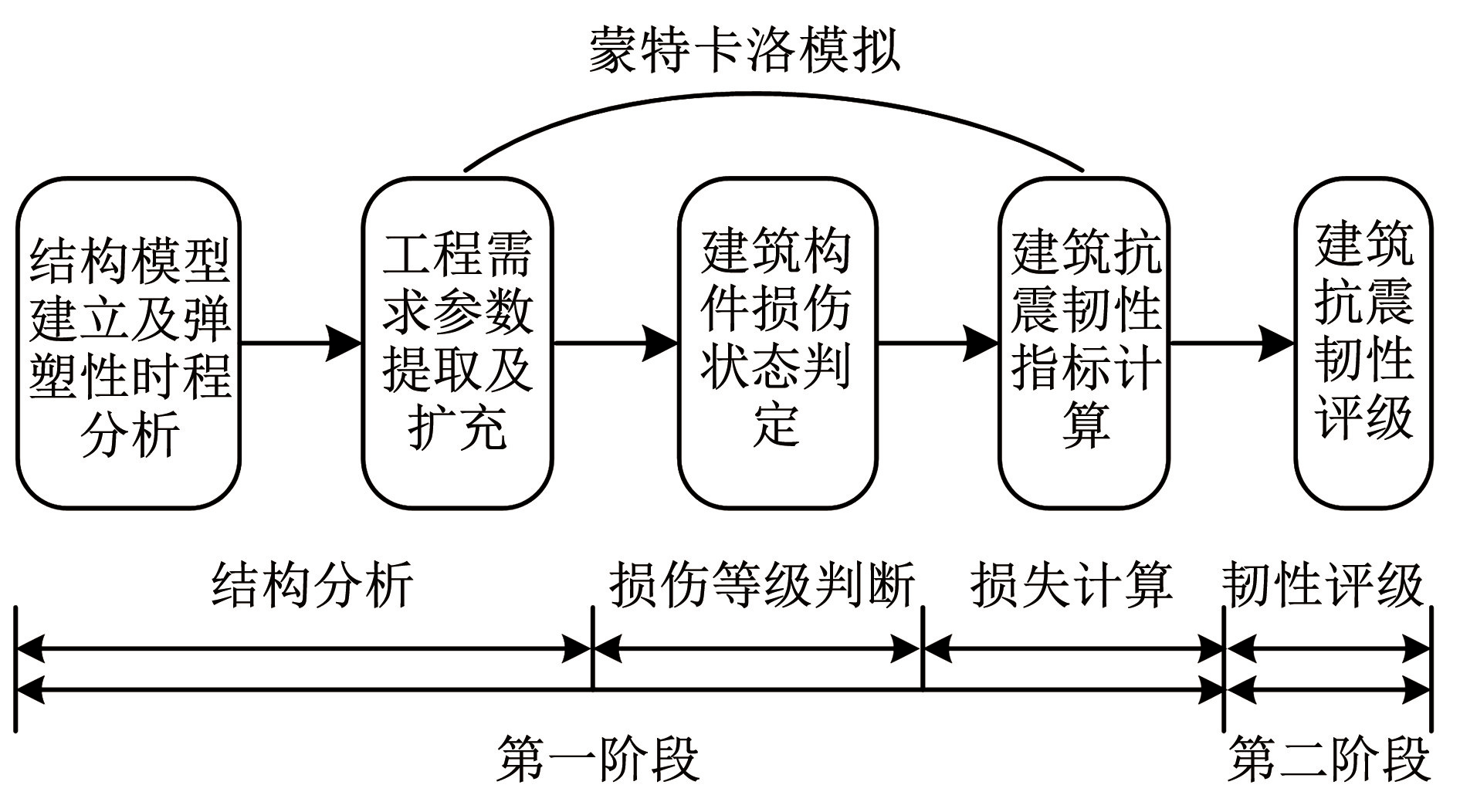
图8建筑抗震韧性评价基本流程
Fig.8Fundamental assessment process of seismic resilience for buildings
5.1 建筑信息
目标建筑为按照现行中国规范设计的一幢 12 层型钢混凝土框架办公楼,标准层层高 3.9 m,跨度 7.2 m,总高度 47.1 m,总面积 7 776 m 2,抗震设防烈度 8 度,场地类别为Ⅱ类,地震分组为第一组。结构典型楼层截面配筋图见图9。

图9型钢混凝土框架几何尺寸及配筋信息
Fig.9The geometric dimensions and reinforcement information of the SRC frame
5.2 损失评估
损失评估是韧性评级的重要依据,其关键在于建筑损伤等级的判定,而损伤等级的判定依赖于构件易损性函数。主要步骤如下:
步骤一:结构分析。利用 OpenSEES 建立算例框架数值模型,并以 FEMA P695 推荐的 22 条地震动记录为基本地震输入,采用地面峰值加速度(PGA)调幅至多遇及罕遇地震水平下进行动力分析。结构工程需求参数均值见图10。
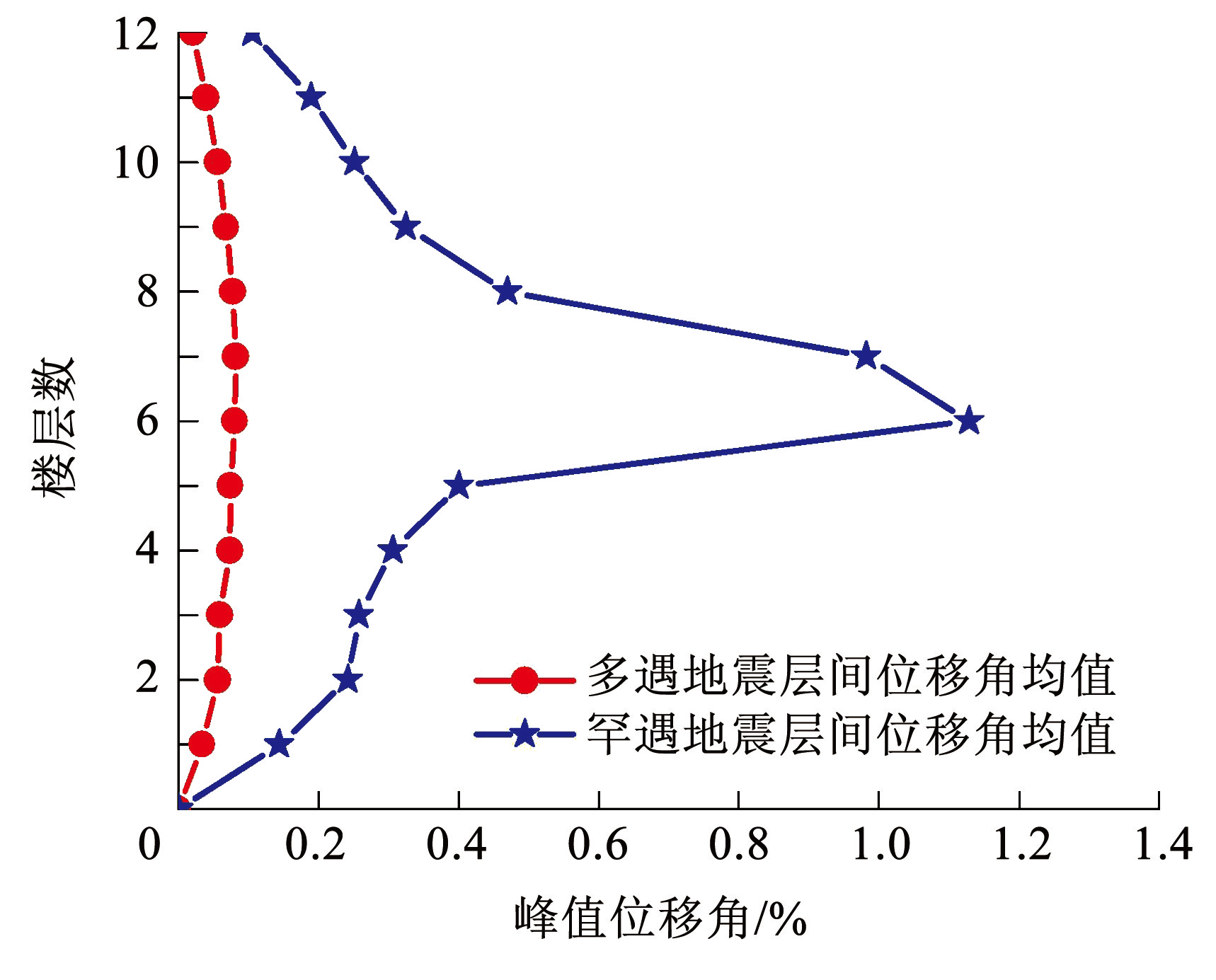
图10多遇和罕遇地震下结构的层间位移角
Fig.10Inter-story drift under frequent and maximum considered earthquakes
步骤二:损伤等级判断。 《建筑抗震韧性评价标准》 [2]采用蒙特卡洛模拟方法对工程需求参数矩阵进行扩充,扩充的过程相当于对结构进行模拟弹塑性分析。以每次蒙特卡洛模拟得到的工程需求参数,结合构件易损性函数确定其各级损伤状态的发生概率,并采用生成随机数 R 的方法确定最终损伤状态。在本算例分析中,由工程需求参数结合 3.3 节提出的易损性曲线可得多遇及罕遇地震下 SRC 柱各损伤等级的概率,见表6。由表6可知,在多遇地震下,层间位移角较小,SRC 柱未发生损伤; 在罕遇地震下,仅 5~8 层发生损伤且仅出现了 DS1~DS2两种损伤等级。其中第 6 层的层间位移角最大为 1.13%。此时,当 0.71≤R≤1 时,未发生损伤; 当 0.14≤R <0.71 时,损伤等级为 DS1; 当 0≤R <0.14 时,损伤等级为 DS2。
表6多遇及罕遇地震下 SRC 柱达到各损伤状态的概率
Tab.6 The probability of SRC columns reaching various damage states under frequent and maximum considered earthquakes

步骤三:损失计算。主要包括 3 个方面,即修复费用、修复时间及人员伤亡。计算结果取决于由步骤二判定的建筑损伤等级,详细计算方法见文献[2]的第 6~8 章,本算例结构计算结果见表7。
5.3 韧性评价
抗震韧性的评级方法主要依据建筑修复费用、建筑修复时间和人员伤亡 3 个指标。 3 个评价指标均采用星级制进行评级,星级划分见《建筑抗震韧性评价标准》 [2]。最终建筑的抗震韧性等级应综合考虑修复费用、修复时间和人员伤亡 3 项指标的等级进行评价,并取 3 项评价指标的最低等级作为该建筑的抗震韧性等级。本算例的评级结果见表7,由表7可知,该型钢混凝土框架结构的韧性等级为三星。值得注意的是,本案例分析仅为了说明 SRC 柱易损性函数在结构抗震韧性评价中的作用,因此在评价过程中仅考虑了柱损伤产生的影响,并未考虑其他非结构构件损坏造成的地震损失。
表78 度设防下 SRC 框架结构抗震韧性等级评价
Tab.7 Resilience ratings of SRC frame structures with fortification level of 8

6 结论
1)延性 SRC 柱对应损伤等级 DS1~DS5 的易损性函数的中位值分别为 0.92%、1.86%、2.65%、 3.27%、3.99%,对数标准差分别为 0.36、0.48、0.38、 0.38、0.38; 偏脆性 SRC 柱对应损伤等级 DS1~DS3 的易损性函数中位值分别为 0.69%、 1.81%、 2.30%,对数标准差分别为 0.58、0.46、0.46。
2)相同损伤等级下延性构件的位移角中位值总是高于偏脆性构件,且随着损伤程度的增大,两者差距更加明显。而偏脆性构件的 βi 均高于延性构件,是因为其脆性破坏特点提高了易损性曲线的离散度。
3)在相同的轴压比分组下,三、四级框架柱的易损性曲线超越概率高于一级框架柱,说明三、四级框架柱的抗震能力较差。在低轴压比工况下,相同损伤等级偏脆性 SRC 柱的 ΔPf,max要明显高于延性 SRC 柱。而在高轴压比工况下,抗震等级对延性和偏脆性 SRC 柱的 ΔPf,max影响并不显著。
4)相同抗震等级下,轴压比对延性构件易损性曲线的影响更显著。其对延性构件各损伤等级下 ΔPf,max的影响介于 38%~63%,而对偏脆性构件则为 20%~54%。轴压比对一级框架柱各损伤等级下破坏概率的影响高于其他等级框架柱。对于延性一级框架柱,其 ΔPf,max最大可达 63%。对于偏脆性构件,轴压比对一、二级框架柱的影响( 21%~54%)高于三、四级框架柱(20%~23%)。
5)建立的 SRC 柱易损性函数与《建筑抗震韧性评价标准》相容,为 SRC 结构的抗震韧性评估提供支持。



